金属纳米结构下气体位置对谐波截止能量的影响

栗博文，王佳乐，刘 航

（辽宁工业大学 化学与环境工程学院，辽宁 锦州 121001）

近20年强场动力学研究方向，高次谐波已经成为研究最为广泛的一种现象[1]。其主要应用在于产生孤立阿秒脉冲和探测原子、分子或固体内的超快电子运动[1-2]。

基于1993年提出的半经典三步模型[3]，高次谐波的辐射过程可由电离、加速和回碰过程组成。并且，谐波截止能量对于产生高光子能量光源具有非常重要的作用。根据三步模型的描述，谐波截止能量在IP+3.17UP处。这里Ip是体系电离能，其与选择的体系有关，对谐波高能区影响不大；UP是电子有质动力势能，与激光强度呈正比，与激光频率平方呈反比。因此，为了延伸谐波截止能量并获得高能区的谐波连续光谱，研究人员提出了很多增大谐波截止能量的方法。例如：(1)利用高强度激光场驱动气体产生高能谐波截止能量[4]；(2)利用低频激光场来增大谐波截止能量[5]；(3)利用调频激光场改变激光瞬时频率进而延伸谐波能量[6]；(4)利用组合激光场调控激光波形进而获得高能谐波平台区[7]。

最近10年，研究人员发现当激光场在特殊金属纳米结构下时会呈现空间非均匀性，导致激光强度随空间变化。若此时再加入气体，则产生的谐波截止能量会得到延伸[8-10]。虽然最近10年空间非均匀场驱动气体产生高次谐波已经被广泛研究[8-10]，但是入射气体位置对谐波的影响却少有报道。因此，本文理论研究了3 种不同金属纳米结构下，射入气体空间位置对谐波截止能量的影响。这对深入研究空间非均匀场下谐波辐射和超快电子运动提供了一定参考。

1 理论方法

本文研究体系为单个He 原子，与激光场作用的薛定谔方程为[11](这里只给出主要公式，具体求解过程参考文献[11])：

其中，x、t和Ψ分别为电子坐标、时间和波函数；为非均匀激光场，其中E和ω1分别为激光场振幅和频率；激光波包f(t)选为高斯波包；为激光场非均匀形式；β为非均匀参数，具体参见文献[12]。

方程求解方法为二阶分裂算符方法[11]。本文纳米结构的宽度选择为g=1、16、14 nm。对于以上3种宽度，电子运动范围分别在[-170 a.u.,170 a.u.]，[-150 a.u.,150 a.u.]和[-130 a.u.,130 a.u.]。因此，为了模拟真实环境，当采用上述3 种不同类型纳米结构时需在±170、±150、±130 a.u.处加入吸收势。高次谐波光谱为：

其中：

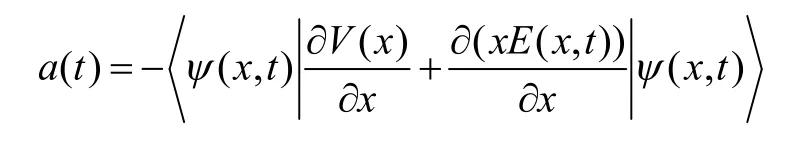
2 结果与讨论

图1 给出5 fs-800 nm激光场入射到纳米结构下时所产生的非均匀激光场场强的空间非均匀性。入射激光强度为100 TW。由图可见，激光强度随空间位置远离纳米结构中心点而增强。并且，随着纳米结构增宽，激光强度可以得到更大的增强，例如：在14、16、18 nm 纳米结构边缘处，激光强度可以分别增强到1.3E、1.45E、1.6E。

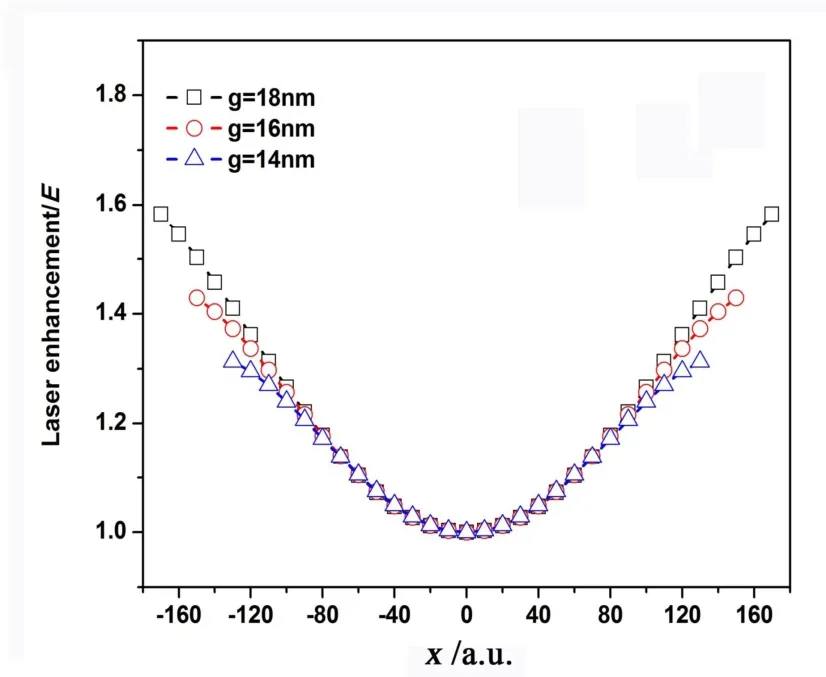
图1 3 种纳米结构下非均匀激光场场强随空间位置的变化

根据三步模型的描述，谐波截止能量与激光强度呈正比，也就是说，更强的激光强度应该可以获得更大的谐波截止能量。为了研究上述3 种纳米结构下，谐波截止能量与非均匀激光场强(或者说是气体入射位置)的关系，图2 给出了上述3 种纳米结构下谐波截止能量随气体入射位置的变化。如图所示，当气体入射位置与中心点距离小于60 a.u.时，3 种纳米结构下谐波截止能量随入射位置增大而增大。并且它们之间的差距不是很大。但是，当气体入射位置大于60 a.u.时，谐波截止能量的延伸体现出明显差距。具体来说，(1)对于14 nm 的纳米结构来说，谐波截止能量在气体入射位置60～105 a.u.区间缓慢延伸，并且在105a.u.处产生最大谐波截止能量46ω1。随后，谐波截止能量随着气体位置增大而减小。(2)对于16 nm 的纳米结构来说，谐波截止能量在气体入射位置60～120 a.u.区间快速延伸，并且在120 a.u.处产生最大谐波截止能量56ω1。随后，谐波截止能量随着气体位置增大而减小。(3)对于18 nm 的纳米结构来说，谐波截止能量在气体入射位置60～135 a.u.区间急速延伸，并且在135 a.u.处产生最大谐波截止能量72ω1。随后，谐波截止能量随着气体位置增大而减小。根据三步模型的描述，高强度激光场应该产生高能光子。但是，为什么随着非均匀激光场强度增大，谐波截止能量会出现极值？为了解释这一现象，本文对纳米结构下电子运动做了进一步分析。基于三步模型可知，电子在激光场下运动的最大距离为：

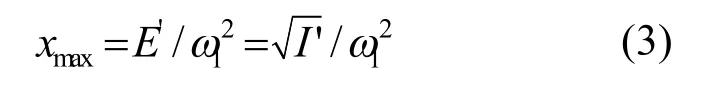
这里Ip是He 原子电离能。根据之前分析谐波截止能量可知，在14、16、18 nm 结构下，最大的激光增强强度分别为nm=4.51I。因此，根据电子运动公式可知，电子在上述3 种纳米结构下的最大运动距离为xmax=25 a.u.(14 nm 结构)；xmax=30 a.u.(16 nm 结构)以及xmax=35 a.u.(18 nm 结构)。由于上述3 种纳米结构存在一定的宽度范围，即[-130 a.u.,130 a.u.]、[-150 a.u.,150 a.u.]、[-170 a.u.,170 a.u.]。因此，气体入射位置与电子最大运动距离之和应该小于纳米结构边缘到中心点的距离。如果设气体入射位置为xin，则，xin+xmax≤130 a.u.(14 nm 结构)，150 a.u.(16 nm结构)，170 a.u.(18 nm 结构)。因此，产生最大谐波截止能量的最佳位置为xin=105 a.u.(14 nm 结构)，xin=120 a.u.(16 nm 结构)，xin=135 a.u.(18 nm结构)。通过上述分析可知，当入射气体位置小于最佳位置时，电子获得能量并且返回母核辐射高次谐波。但是，当气体入射位置大于最佳位置时，获得高能的电子运动距离更大，会超过纳米结构边缘，因此被纳米结构边缘所捕获，进而不能返回母核发射高能光子。这也是谐波截止能量随着入射气体位置超过最佳位置而减小的原因。

图2 3 种不同纳米结构下谐波截止能量随气体位置的变化

3 结论

谐波截止能量随着入射气体位置增大而呈现先增大再减小的现象，并且存在一最佳入射位置，当气体在该位置入射时会产生最大谐波截止能量。随后，分析电子在纳米结构中的运动显示，有限的纳米结构宽度是产生谐波截止能量极值的原因。最后需要说明，金属纳米结构下谐波截止能量存在极值的现象与所选取的气体无关，即任何气体都会存在一个固有的谐波辐射极限值。