基于差分进化算法的X荧光重叠峰的分解
廖先莉, 黄进初, 赖万昌, 辜润秋, 王广西, 唐 琳, 翟 娟
1. 成都理工大学核技术与自动化工程学院, 四川 成都 610059 2. 成都大学信息科学与工程学院, 四川 成都 610106
引 言
对于谱峰重叠问题, 一般用数学解析法进行重叠谱分解, 谱峰重叠数学分解方法的研究, 对荧光谱进一步的定量、 定性分析都有十分重要的意义, 现阶段已有不少相关的研究报告[1-3]。 其中杨熙等提出了GMM-SDR模型和粒子群算法相结合的重叠谱的解谱方法[1]; 胡耀垓等运用曲线拟合完成了光谱重叠峰解析方法[2]; 徐喜荣等提出了一种基于小波变换和连续Hopfield神经网络的谱图重叠峰解析策略[3]; 目前还没有一种算法被公认为没有局限性的数学解谱方法, 比如曲线拟合度不够高, 易陷入局部收敛, 使用限制条件不易满足。
本文在高斯混合统计模型的基础上, 提出两种情况下的参数模型, 利用差分进化算法全局搜索优势, 得到了重叠谱的最优分解模型。 两种模型下的解谱结果误差范围内都是有效的, 但是解谱精度却不相同, 为类似数学解谱方法提供参考, 同时该方法的搜索速度快, 种群规模对寻优结果的影响比较小, 结合了光谱的随机物理特性, 保证的原谱数据的“零损失”。
1 算法与原理
1.1 统计模型GMM
一种融合了参数估计法和非参数估计法优点的修正模型, 模型为
(1)
其中ai为各分支的权重, 且满足
(2)
式(1)中,M为分支数,ui和σi表示第i分支的均值和标准差, 由各个分支的权重、 均值、 标准差构成了差分进化算法寻优体参数, 所得的最优解, 即为重叠峰分解后各个小峰的参数。
如果不能提前确定GMM模型中参数间的关系, 认为其是相互独立的, 建立模型为GMM参数独立模型, 模型参数为θ=[a1,a2, …,aM;u1,u2, …,uM;σ1,σ2, …,σM]。
如果能够知道重叠谱各个小峰参数间的关系, 建立模型为GMM参数关联模型, 可以通过这种关系减少差分进化算法寻优个体的参数个数, 比如均值和标准差间存在线性关系σi=σ1ui/u1, 模型参数为θ=[a1,a2, …,aM;u1,u2, …,uM;σ1], 下文中均以均值和标准差间存在的线性关系建立GMM参数关联模型。
1.2 GMM模型参数的差分进化算法估计
差分进化算法是模拟自然界物种进化原理的一种寻优算法, 算法通过对父代个体进行变异、 交叉操作, 生成新一代个体, 选择子代和父代个体中满足目标条件且适应度值最优的个体作为本次寻优的结果, 经过多级迭代, 使搜索结果逐渐趋近全局最优解[4]。 具体方法如下:
(1) 初始化种群
GMM参数独立模型个体的维数为3M, 个体中元素ai,ui和σi在有限区间上随机生成, 种群中粒子规模为NP。
GMM参数关联模型个体维数2M+1, 个体中元素ai,ui和σi在有限区间上随机生成, 种群中粒子规模为NP。 整个寻优过程需满足条件σi=σ1ui/u1, 其中i=2, 3, …,M。
为了满足GMM模型中式(2)的条件, 首先要对模型参数ai做归一化处理, 使得参数ai的取值范围在0到1之间, 方便后续的运算。 在对寻优得到的参数进行还原, 方便得到的模型曲线和实际谱线对比。
(2) 适应度值的评估
种群中的每一个个体对应一个适应度值, 适应度值由式(3)算得, 每一代种群中适应度值最小的个体为这一代种群中的最优个体, 多代寻优后适应度值不变时, 搜索结束, 得到的参数θ为全局最优个体, 即为我们所求的分解模型参数。
(3)
由式(3)可知,g(i)为随机序列(道址)对应的计数值, 由随机序列x(i)带入GMM模型得到的值取对数后值为负数,P(x(j)/θ)越大f(θ)越大,Y(θ)的值越小, 所得个体越优, 该方法充分使用了测量所得的所有随机数据, 保证了原谱数据的“零损失”。
(3) 变异策略
采用式(4)的变异策略来更新种群个体, 其中,V(i)表示变异后的第i个个体,X(i)为变异前的第i个个体,X(r(1))为变异前的第r(1)个个体,X(r(2))为变异前的第r(2)个个体,r(1)和r(2)是[0, NP]范围内产生了不等于i的整数,F为变异缩放因子。
V(i)=X(i)+F(bestX-X(i))+F(X(r(1))-X(r(2)))
(4)
(4) 交叉策略
如式(5)所示, 个体中的X(i,j)经过变异策略后变为个体V(i,j), 若[0, 1]之间生成的随机数正好等于交叉概率CR, 或者1到Dim之间随机生成的整数jrand等于j时, 新生成个体中的U(i,j)等于V(i,j), 否则U(i,j)为变异前的X(i,j), 该交叉策略确保了最新产生的个体中至少有一个U(i,j)=V(i,j)。
(5)
(5) 选择策略
如式(6)所示, 当经过交叉、 变异后新产生的种群个体所对应的适应度函数值小于原来个体所对应的适应度函数值时, 下一代种群这个位置上的个体变为最新产生的种群个体, 否则, 下一代种群中这个位置上的个体保持不变。
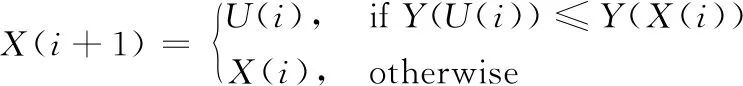
(6)
(6) 终止条件
迭代次数满, 或者最优适应度值Y(θ)连续多次不变时 , 算法终止, 否则返回(3)继续搜索。
一直到满足终止条件得到最优个体, 得到各个分支高斯函数的权值、 均值和均方差, 完成重叠峰分解 。
2 重叠峰的分解
采用离散直接抽样方法产生随机数值x(1) ,x(2) , …,x(N), 由这些随机数的统计分布构成X荧光重叠峰, 重叠峰由几个峰位十分接近的高斯峰重叠而成[5-7], 本设计以重叠谱解谱为重点, 本底计数已扣除, 下面将依次介绍两类重叠峰的分解过程。
2.1 三峰分解
图1为三峰重叠谱, 峰位为210, 200和190, 面积分别为25 000, 15 000和10 000, 即归一化后权重分别为0.5, 0.3和0.2, 横坐标为道址, 纵坐标为计数。
采用GMM参数独立的模型, 设种群的个体为X=[a1,a2,a3;u1,u2,u3;σ1,σ2,σ3], 各参数的取值下限[0.01, 0.01, 0.01; 160, 160, 160; 4, 4, 4], 取值上限[1, 1, 1; 250, 250, 250; 8, 8, 8], 选择取值范围内的随机数初始化种群, 种群规模50, 最大迭代次数1000, 缩放因子CR为0.1和交叉概率F为0.1。 采用GMM参数关联的模型, 则提前知晓均值和标准差间的线性关系σi=σ1ui/u1, 种群个体为X=[a1,a2,a3;u1,u2,u3;σ1], 取值范围从[0.01, 0.01, 0.01; 160, 160, 160; 4]到[1, 1, 1; 250, 250, 250; 8], 选择取值范围内的随机数初始化种群, 种群规模50, 最大迭代次数1 000, 缩放因子CR为0.1和交叉概率F为0.4。
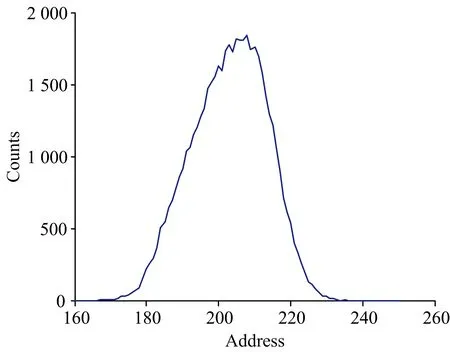
图1 三峰重叠谱
如表1可知, 参数独立模型和参数关联模型分别得到的权重最大误差为8.15%和2%, 峰位最大误差为0.30%和0.06%, 标准差的最大误差为7.5%和1.35%。

表1 权重、 峰位和标准差的比较

图2 原始谱、 GMM参数独立曲线、 分解峰
图2和图3分别为两种模型下原始重叠谱和分解谱的拟合情况。 已经能够明显观察到运用GMM参数关联模型对重叠谱进行分解的精度比运用GMM参数独立模型对重叠谱进行分解的精度高。

图3 原始谱、 参数关联GMM谱、 分解峰
2.2 四峰分解
如图4所示, 为四峰重叠谱, 各子峰的峰位分别为200, 210, 225和240, 峰面积分别为20 000, 30 000, 30 000和20 000, 即归一化后权重分别为0.2, 0.3, 0.3, 0.2, 重叠严重。
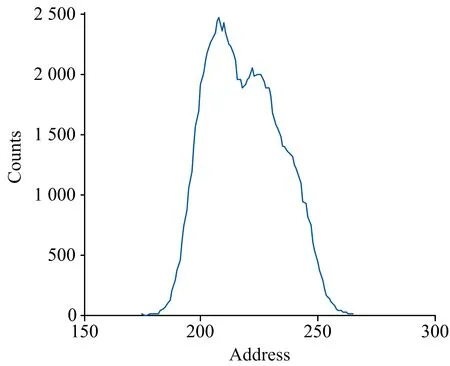
图4 四峰重叠谱
设置种群个体50, 如果选择GMM独立参数的模型, 则每个种群个体有12个参数, 它们的取值范围从[0.01, 0.01, 0.01, 0.01; 175, 175, 175, 175; 4, 4, 4, 4]到[1, 1, 1, 1; 265, 265, 265, 265; 8, 8, 8, 8], 如果能够提前知道重叠谱参数间的关系, 得到GMM的相关联参数模型, 比如均值和标准差间的线性关系δi=δiui/u1, 则每个个体参数10个, 它们的取值范围从[0.01, 0.01, 0.01, 0.01; 175, 175, 175, 175; 4]到[1, 1, 1, 1; 265, 265, 265, 265; 8], 两种模型寻优的迭代次数为1 000, 交叉概率F=0.8, 缩放因子CR=0.8。
如表2可知, 参数独立模型和参数关联模型分别得到的权重最大误差为8.3%和4.3%, 峰位最大误差为0.12%和0.13%, 标准差的最大误差为5.04%和0.45%。

表2 权重、 峰位、 均方差的比较
如图5和图6所示, 分别为通过独立GMM模型和相关联GMM模型, 对原始重叠峰进行分解后的各峰拟合情况。 已经能够明显观察到运用GMM参数关联模型对重叠谱进行分解的精度比运用GMM参数独立模型对重叠谱进行分解的精度高。
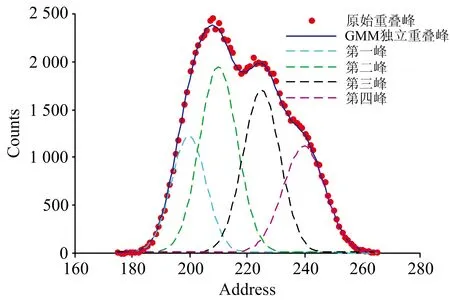
图5 原始谱、 GMM参数独立曲线、 分解峰

图6 原始谱、 参数关联GMM谱、 分解谱
每次寻优分解的效率和搜索结果的精度不尽相同, 略有差异, 相对而言, GMM参数关联模型运用差分进化算法搜索结果更加稳定, 精度也相对较高。
2.3 重叠谱峰的分解实例
取深井中的岩屑作为基样, 加入镝粉, 磨匀配置镝元素含量分别为20, 5和2 μg·g-1的三种样品, 由于岩屑中本身含有Mn和Fe元素, 当加入Dy元素后, 三种元素的部分特征X射线会发生谱重叠现象, 如图7所示, 为三种样品用X荧光仪测得的全谱图。
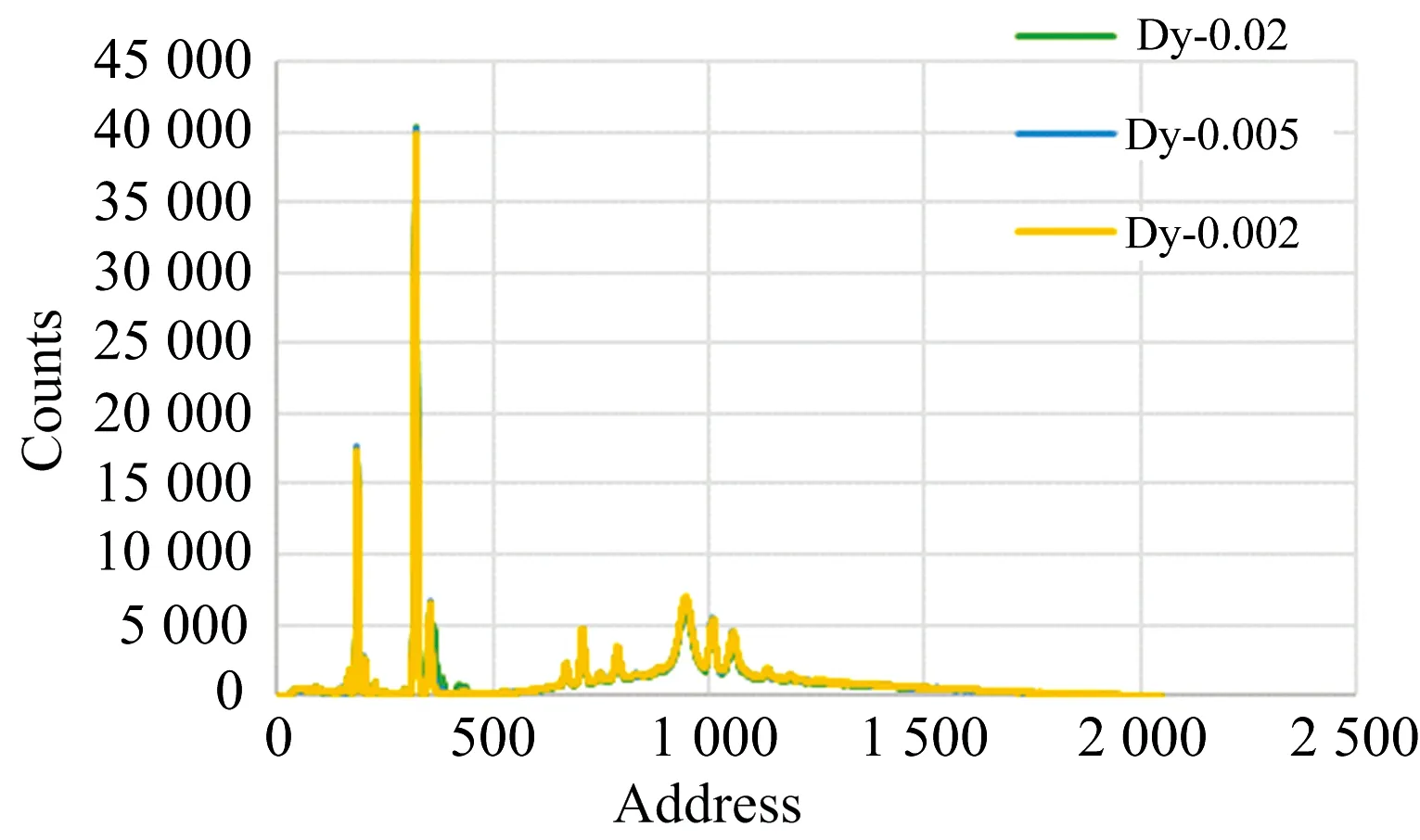
图7 样品能谱图
Mn元素的Kβ系的特征X射线能量为6.49 keV, Fe元素Kα系的特征X射线能量为6.403 keV, Dy元素Lα系的特征X射线能量为6.495 keV, 由于Dy元素含量比较低, 为了能够更好的分析谱重叠情况, 对图进行局部放大如图8所示, 为三种元素的重叠峰。

图8 实测三峰重叠谱
将X荧光仪实测谱线重叠峰相关数据取出扣除本底后导入matlab中, 根据建立的独立GMM模型, 对重叠谱进行分解, Dy元素含量为20 μg·g-1的样品, 分解后各峰的情况如图9所示。
独立GMM模型对三种样品的重叠谱进行分解, 得到Dy元素的含量分别为19.10, 5.27和2.27 μg·g-1, 相对误差分别为-4.5%, 5.4%和13.4%。 可见用该种方法进行重叠峰的分解时, 随着元素含量降低, 分解得到的结果相对误差增大。
在已知所求元素种类的情况下, 可以提前已知峰位间的关系, 建立相关联GMM模型, Dy元素和Mn元素的特征X射线能量差不多, Dy元素Lα系的特征X射线能量为6.495 keV, 可得式(1)中的u1=u2和u3=0.986 6u1, 模型中参数个数由9个变成了7个, 根据建立的相关联GMM模型, 对重叠谱进行分解, Dy元素含量为20 μg·g-1的样品, 分解后各峰的情况如图10所示。
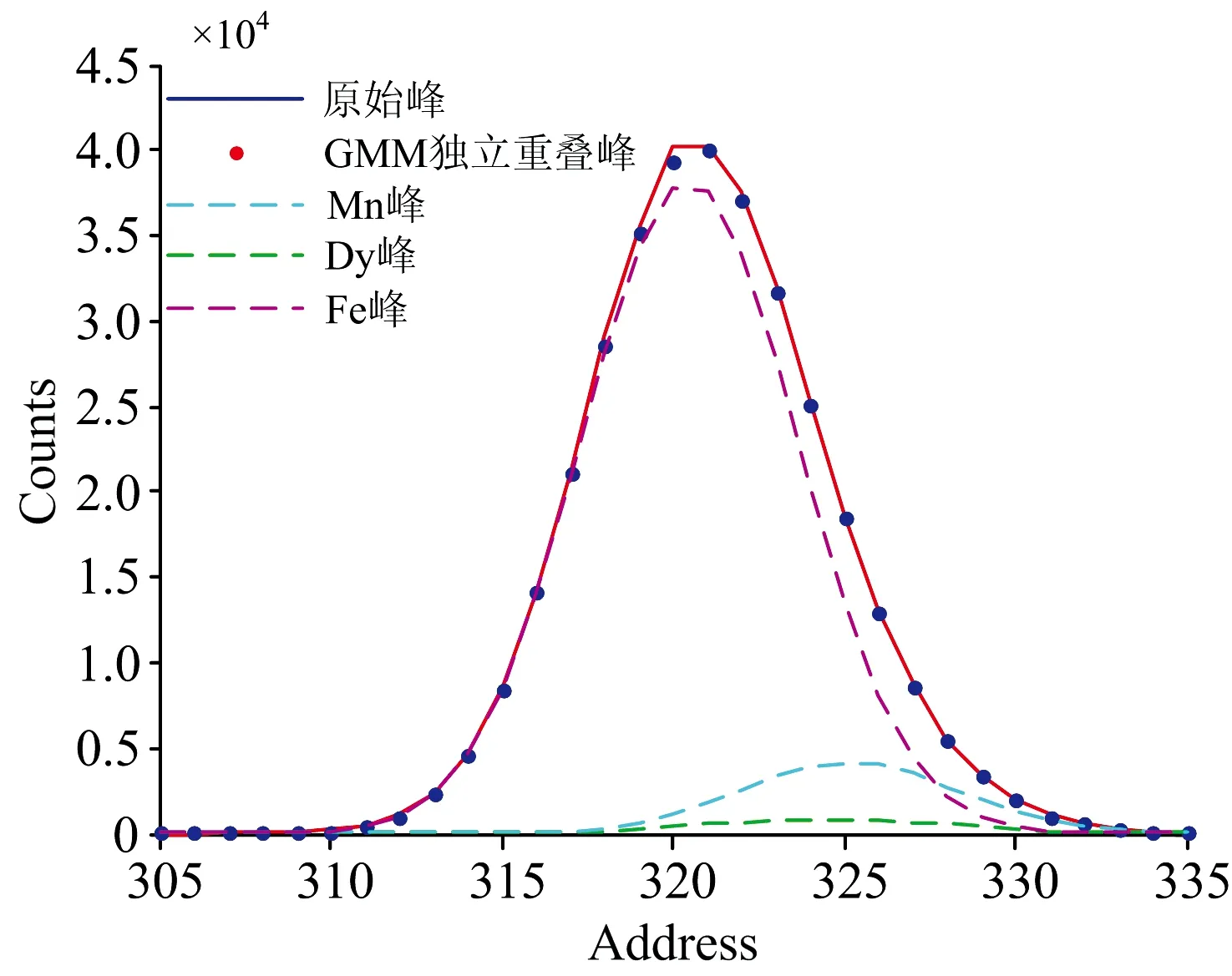
图9 原始谱、 GMM参数独立曲线、 分解峰
相关联GMM模型对三种样品的重叠谱进行分解, 计算得到Dy元素的含量分别为20.18, 4.85和2.15 μg·g-1, 相对误差分别为0.9%, -3%, 7.5%, 可见该方法解谱得到的结果相对误差比独立GMM模型解谱得到结果的相对误差小一些, 元素含量越低, 脉冲计数越少, 分解得到的结果相对误差越大。
由实验可知, 两种方法进行重叠谱分解时, 能够知道各峰间的关系, 建立相关联GMM模型, 减少参数个数, 分解后的精度更高, 但是随着元素含量的降低, 分解测量的精度降低了。

图10 原始谱、 参数关联GMM谱、 分解谱
3 结 论
运用文中方法对重叠峰的分解结果表明, 两种模型下, 均能实现重叠谱的分解, 从模拟仿真可知, 针对相对复杂的重叠峰两种模型得到的分解结果精度都较高, 但是GMM参数关联模型的分解精度比GMM参数独立模型的分解精度明显高一些。 从三峰重叠的分解实例来看, 由于实际测量过程中对测量结果的影响因素相对复杂一些, 分解计算得到的结果较仿真计算结果相对误差大一些, 两种方式的结果表明, 如果能够提前得到各个相互重叠小峰之间的关系, 建立相关联GMM模型, 减少寻优参数个数, 对提高复杂峰的分解精度是非常重要的。

