级联环境下量子加速的调控

白雪敏

（晋中学院物理学院，山西晋中030619）

0 引言

由于任何系统都不可避免地受到周围环境的影响，如何检测系统的量子态演化速度受到国内外研究者的广泛关注.量子系统从初始态达到目标量子态所需要的最小演化时间被称为量子速度极限时间.近年来，人们对封闭系统和开放系统的量子速度极限时间问题做了大量的研究［1～4］.量子速度极限时间相关问题研究在量子物理的许多领域中都起着重要的作用，例如，量子计算、量子控制和量子计量［5～7］等等.最近，针对系统中纠缠度对量子极限时间的作用［8］、退相干与量子极限时间之间的微妙联系［9～10］，开放系统下初始状态对量子极限时间的影响以及在量子相变与量子极限时间的联系等课题，许多文献都展开了研究［11］.特别是非马尔科夫性可以加速量子系统的演化在不同的噪声环境下的系统中被做了大量的研究.关于实验在弱驱动光腔电动力学系统中的非马尔科夫性可以加速量子系统演化已在文献［12］中被报道.在此基础之上，我们将研究级联环境中原子激发态布居数以及非马尔科夫性对系统量子演化速度的影响，我们研究的是一个量子比特被嵌入在两个耦合腔中的一个腔内的系统.由于模型参数的变化，本系统也可发生马尔科夫到非马尔科夫转变的现象.我们研究该量子系统中环境参数对量子速度极限时间的影响.当量子速度极限时间与驱动时间相等τQSL=τ，这意味着进化已经沿着最快的路径，不具备进一步加速演化的潜力.然而当τQSL＜τ，τQSL越小代表该系统潜在的加速能力越大［13］.在这种情况下，随着腔-腔耦合强度J的增大，系统的量子态演化可以从没有加速到有加速.原子激发态布居数与非马尔科夫性对量子极限时间影响较大.研究表明，即使是两个量都对量子加速起到作用，但非马尔科夫性最终决定了对量子态演化的加速.

1 物理模型以及基本概念

我们考虑一个量子比特被放置在一个有损腔C1而C1又与另一个有损腔C2相互作用组成的量子系统，它的哈密顿量为如下形式（ħ=1）：

这是级联环境中一个量子比特系统的哈密顿量.σ±是量子比特的上升和下降算符，ω0是量子比特基态｜0〉和激发态｜1〉之间的转换频率，（a1）为Ci腔的产生（湮灭）算符以及腔场频率为ωi（i=1，2）.J表示两腔之间的耦合强度，参数κ代表比特和腔之间的耦合强度参数.为了简便，我们令ω1=ω2=ω且ω0=ω+δ，这里δ是量子比特和腔之间的失谐.考虑两腔的耗散，可以通过主方程得到整个系统随时间演化的密度矩阵为：

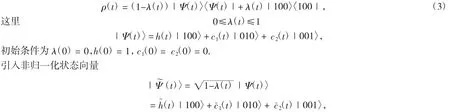
密度矩阵变形为

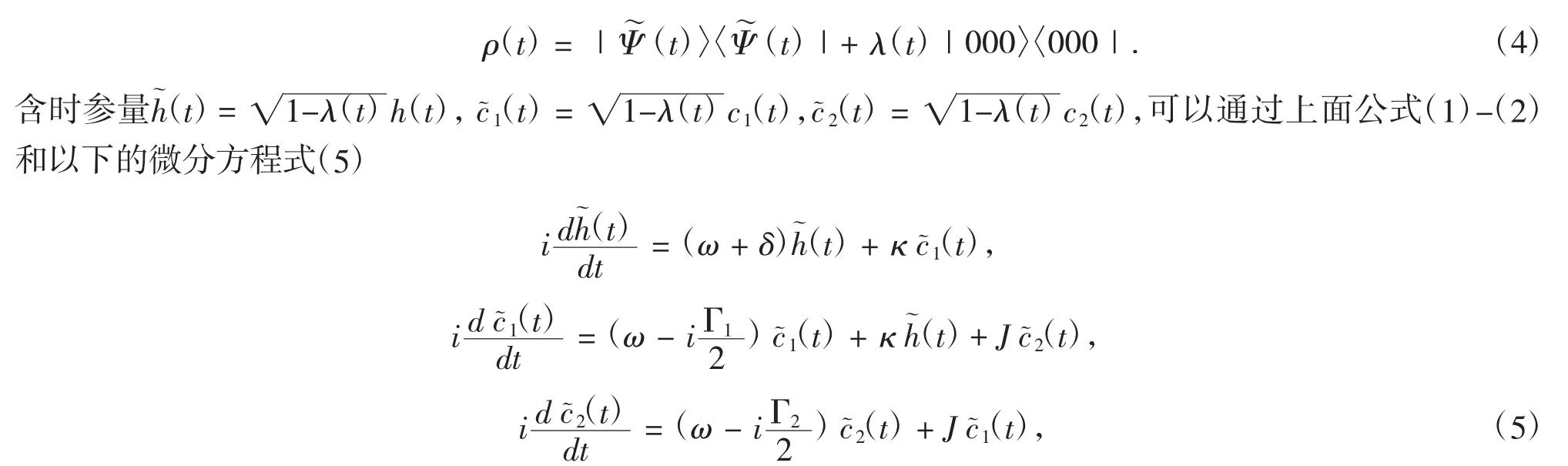
通过标准拉普拉斯转换和数值计算，我们可以得到单量子比特的约化密度矩阵，在基矢 ｛｜ 1 〉，｜0〉｝下可展开为

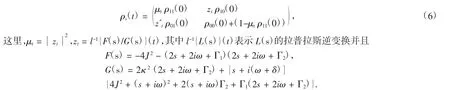
3 量子加速

首先，我们简要地给出了与本文第二部分中描述的模型相对应的单量子比特开放系统的量子速度极限推导形式.根据冯诺依曼不等式和柯西-施瓦茨不等式，开放系统的最初量子态ρ（0）=｜Ψ0〉〈Ψ0｜与其目标量子态ρ（τ）之间的量子速度极限时间满足方程

在这一节，我们计算了初始状态ρ（0）与最终状态之间的量子速度极限时间τQSL，其中驱动时间为τ.为了既方便又不失一般性，初始状态被假设为激发态ρ（0）=｜1〉〈1｜.上述模型的QSL时间τQSL可导出为

其中，μt表示τ时刻激发态的布居数，可以从方程（6）中计算获得.显然，τQSL与给定驱动时间下的原子布居数μt有密切关系.同时，原子布居数μt受到环境各个参数共同的影响.在下面，我们将分别研究J，δ，κ，Γ2对QSL时间τQSL的影响.

为了有效地估计量子加速的过程，我们假设了一个初始状态和一个目标状态，驱动时间τ表示量子系统实际演化时间.不同于封闭系统的动力学状态，在开放系统演化中这两种状态是不正交的.接下来通过分析，我们发现，量子状态演化的最小速度极限时间是由τQSL决定的.τQSL的大小能估计一个量子系统的演化速度.当τQSL＜τ，表示量子系统有加速演化的可能，且τQSL越小量子系统演化得越快.当τQSL=τ，代表系统演化速率是最快的，不存在加速演化的过程.有趣的是方程（8）清楚地表明了τQSL时间与原子布居数μt有关.如果原子布居数μt始终为一，量子比特的状态是不会演化的.这意味着τQSL=0.此外，为了能够使我们更加精细地研究τQSL时间，描绘迹距离时间演化的非马尔科夫性被引入，它定义为如下式子：

其中σ（t，ρ1，2（0））=ρ˙（ρ1（t），ρ2（t））为迹长的改变率.这里，积分区域是σ＜0的整个区域，并对所有可能的初态取极大值与对应极小值之差.

根据文献［16］，当ρ1（0）=｜0〉〈0｜且ρ2（0）=｜1〉〈1｜时，也就是D（ρ1（t），ρ2（t））=μ.我们可以把非马尔科夫表示成如下式子

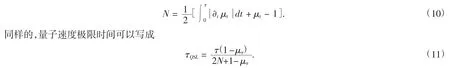
这表明τQSL时间不仅依赖于原子激发态布居数μt，而且在演化时间τ内，非马尔科夫效应也可以加速系统的演化.式（11）意味着量子态从没有加速到有加速只是马尔可夫环境变成非马尔科夫环境出现的现象.当N=0时，τQSL=μt.这是非马尔科夫效应N和激发态原子布居数μt两个量之间共同作用最终决定了系统量子态的演化速度.对于开放量子系统，如果系统与环境相互作用出现信息回流的非马尔科夫效应或原子激发态不计数增大，都可以加快量子系统的演化速度（或者说潜在的加速是可以实现的）.

4 量子加速动力学演化

我们通过数值计算展示了量子速度极限时间τQSL在量子比特和腔场C1的耦合强度κ不同的情况下以无量纲场之间耦合强度J/Γ1为变量的动力学演化（见图1）.这里，我们假定第一个腔的耗散率Γ1=1，量子比特和腔之间的失谐 δ=0，第二个腔的耗散率 Γ2=0（图 1（a1)-图 1（a2）），Γ2=1（图 1（a3）-图 1（a4））.从图中可以清楚地看出，当驱动时间τ不同（例如在τ=1和τ=5）的情况下，以无量纲J/Γ1为函数的量子速度极限时间τQSL的性质表现出强烈的不同.当驱动时间τ=1时，腔-腔耦合强度J大于某个值，系统会产生量子加速现象；而当腔-腔耦合强度J小于这个值时，速度极限时间τQSL会保持在一个稳定的值.逐渐增大耦合强度κ的值（从0.2到1），我们观察到量子加速现象但不是很明显.然而在τ=5的情况下，较强的耦合强度κ可以把加速临界点推到较小的腔-腔耦合强度J区域.我们发现，如果量子比特最初弱耦合与腔C1（κ=0.2）其量子系统的演化随着两腔之间的耦合强度J的增大从没有加速变为加速.另一方面增加量子比特与腔之间的耦合强度（κ=0.6，1），量子加速现象会出现在J=0区域，这种现象完全不同于τ=1的情况.此外，对于较长的驱动时间τ，逐渐增大腔-腔之间的耦合强度J，量子加速表现为阻尼振荡行为.相比较，当第二个腔的耗散强度较大为Γ2=1时，量子系统加速行为可以观察到明显受阻（如图1（a1）～1（a4））.在图1（a3）中的量子加速发生点与图1（a1）的相比，会出现在较大点处.最后，当驱动时间τ越大时，阻尼振荡行为越明显（见图 1（a2）～1（a4））.

图1 量子速度极限时间τQSL以无量纲时间J为变量的演化行为

如何解释上述现象呢？为此，我们在图 1（b1）～1（b4）中以与图 1（a1）-1（a4）相同的参数为条件展示了布居数P与非马尔科夫N的动力学演化曲线图.只有当马尔科夫环境变为非马尔科夫环境时，量子系统演化加速现象才会发生.当驱动时间τ=1时（如图1（a1）和1（a3）），量子加速强烈依赖于布居数P与非马尔科夫N，虽然非马尔科夫很小.随着原子与腔耦合强度κ的增大（从0.2到1），非马尔科夫变得更大，但布居数P变得越来越小，随着耦合强度J的增大，我们观察到的量子加速现象没有显著的不同（见图1（a1））.此外，当驱动时间τ=5，量子加速表现为阻尼振荡行为.这种行为可以通过非马尔科夫与布居数两者的阻尼振荡的方式来解释.当第二个腔的耗散强度较大为Γ2=1时，非马尔科夫与布居数两者的振荡行为明显受阻（如图 1（b1）～1（b4））.

图2显示了在腔-腔耦合强度为J=1和J=2的情况下，δ对量子速度极限时间τQSL、非马尔科夫N、布居数P的影响.在图2（a1）中，当|δ|的值大于某一值时系统演化出现量子加速现象.当驱动时间τ=5（见图2（a2）），增加|δ|值，我们观察到τQSL曲线首先达到一个最小值，然后振荡并达到一个最大值或者保持一间段最大稳定值，最后τQSL曲线进化阻尼振荡.相比较，当量子比特与腔弱耦合时（κ=0.2），会出现没有量子加速现象，但在量子比特与腔强耦合的情况下（κ=0.6，1）一直有量子加速现象.在J=2的情况下，在图2（a3）加速现象出现在δ=0这个点，这是完全不同于图2（a1）.在驱动时间τ=5的情况下，我们观察到没有加速区域和最大值点出现在较大|δ|的地方，但区间的大小以及最大值没有变化.为了解释上述现象，通过对比图2（a1-b4），我们可以发现加速的原因在于非马尔科夫N和布居数P，这与图1相似.

图2 量子速度极限时间τQSL以无量纲时间δ/Γ1为变量的演化行为

5 总结

在这篇文章中，我们讨论和分析了级联环境对量子速度极限时间影响的相关问题.特别地，我们可以观察到由两个耦合的腔组成的环境体系可以使嵌入在其中一个腔内的量子比特系统的动态演化实现在马尔科夫和非马尔科夫之间的切换的.这个特性在本文中可以用来解释系统演化加速现象.此外，我们发现腔-腔耦合强度、量子比特与腔的耦合强度、腔的耗散以及驱动时间都极大地影响了速度极限时间的大小.最后，我们发现非马尔科夫性与激发态原子布居数可以共同解释量子加速现象的产生.

我们对量子速度极限时间的研究方案不仅简单，而且可以用来被扩展成两组分或者多组分体系从而满足了复杂的量子信息研究.这项研究工作的结果关于开放量子系统的量子速度极限有新的见解，并为进一步的实验发展打下了基础，有助于更好地保护量子资源.