经历活动过程 积累活动经验

崔旭 李美云

[摘要]活动课是小学数学教学的重要组成部分，是培养学生数学学习能力的关键环节。以“间隔排列”活动课为例，基于“核心素养”的要求，对数学活动进行了重新定位，不仅教给学生活动方式和方法，更重视积累学生的数学活动经验，提升学生的核心素养，提高学生解决问题的能力。

[关键词]活动课;模型经验;思辨能力;核心素养

[中图分类号]

G623.5

[文献标识码] A

[文章编号] 1007-9068（ 2020） 20-0065-03

“数学教育的目标，是让学生用数学的眼光观察现实世界，用数学的思维分析现实世界，用数学的语言表达现实世界。”因此，数学课程标准十分重视培养学生探索规律的兴趣与能力。《数学课程标准（实验稿）》在“数与代数”领域里设计了“探索规律”的内容和要求。下面笔者结合苏教版教材三年级上册“間隔排列”一课谈谈对活动课的一些做法和思考。

一、找一找，感知特点，积累模型经验

【片段一】

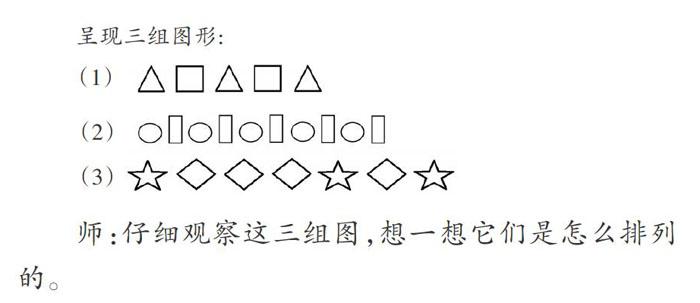
师：仔细观察这三组图，想一想它们是怎么排列的。

生1：第（l）组是一个三角形、一个正方形、一个三角形、一个正方形，一个接着一个排下去的。第（2）组是一个圆形、一个长方形、一个圆形、一个长方形，一个接着一个排下去的。第（3）组是一个星形、三个菱形、一个星形、三个菱形……

师：哪一组的排列方式与其他组不同？（第（3）组）

师：我们先来研究（1）（2）组的排列。它们有什么相同的地方呢？（（1）（2）组都是一个隔着一个排的）

师：像这样（指着第（1）组图），三角形和正方形一个隔着一个排成一行的排列方式，我们把它叫作间隔排列。

师：那什么是间隔排列呢？同桌之间互相说一说。

师：像这样，一种物体和另一种物体一个隔着一个排列的，就叫作间隔排列。

师：在第（1）组中，一个三角形紧接着一个正方形，我们可以把一个三角形和一个正方形看成一组，这样的一组图形中的两个物体称为一一对应。接着往下排，下一个图形是什么？你是怎么想的？第（2）组是把谁和谁看成一组，又是谁和谁一一对应的？继续往下排，下一组图形是什么？我问的是下一组不是下一个哦！你是怎么想的？第（3）组是间隔排列吗？为什么不是？你能改一改其中的一个图形让它成为间隔排列吗？在这组中谁和谁是一一对应的？（教师圈一组，再圈一组），你们看，每组图形都是（☆和◇◇◇）。是呀，这里面每一组都是一一对应的。

师：通过刚才的例子，我们可以看出间隔排列是有显著特点的。

【思考：表示规律的最好形式是数学模型，模型能够最本质、最简明、最数学化地表现规律的数学内容。然而，小学生还不具备利用数学模型解决问题的能力，所以应鼓励他们用自己的方式去表达。教师呈现一种现象，引起学生注意，激发学生探索规律的兴趣;通过“看”“比”“说”“找一一对应”等活动，由表及里逐步突显现象里的规律，这些规律以形象思维的方式保存在学生的经验里，既有比较充分的体验，又不需要刻意去记忆。】

二、数一数，探索规律，培养学生的思辨能力

【片段二】

1.观察

师：仔细观察这幅图，哪些物体是间隔排列的？

师（示范）：兔子和蘑菇是一个隔着一个排列的。还有呢？

生1：木桩和篱笆是一个隔着一个排列的。手帕和夹子也是一个隔着一个排列的……

师：它们的排列有什么规律？我们先来看兔子和蘑菇这一组。看，从左边起，开始是什么？（兔子）结束是什么？（蘑菇）排在第一个和最后一个的物体叫作“两端物体”。每2只小兔子中间有一个蘑菇，蘑菇就叫“中间物体”。

师：这幅图的两端物体一样吗？都是什么？中间的物体是什么？（木桩和篱笆）手帕和夹子呢？通过观察我们发现，这三组间隔排列的两端物体都怎么样？（两端物体相同）

2.猜想

师：当两端物体相同时，两端物体和中间物体数量之间有什么关系呢？同学们可以数一数、比一比，填一填作业纸上的表格，填好后仔细观察，写下你的发现。开始活动——（反馈表格里数据）

师：你有什么发现？

生2：不论是多1还是少l，我们都可以说每排两种物体的数量相差1。（板书：相差1）

师：这只是我们的初步发现，只能说是猜想。仅仅凭这3组数据就能说明我们的猜想一定是正确的吗？当然不行，需要我们进行大范围的验证。（板书：验证）

3.验证

师：老师为你们每人准备了一份学具，先不动，仔细听要求，请选择一些学具摆一摆、排一排、数一数、想一想，两端物体和中间物体各是什么？各有几个？它们的数量有什么关系？验证一下我们的猜想是否正确，开始活动。

师：你摆的图形是间隔排列吗？说说每种图形摆了几个，符合刚才的发现吗？

生3：我摆的时候放了7个圆，6个长方形，我发现圆比长方形多1个，符合我们刚才的发现。

师：有没有不同的结论？看，这位同学摆的是间隔排列吗？和刚才那几幅图有什么不同？我们又有了新发现：两端物体不相同，两种物体的数量同样多。现在我们又多了一种发现，它当然还是猜想，请验证两端物体不同时它们的数量是否一定相等。（学生摆）

师：你们摆的是间隔排列吗？圆有几个？三角形有几个？符合我们刚才的发现吗？

师：有没有不符合这个结论的例子？（没有）好，活动结束，请同学们把学具全部收好。

师：现在能说说你们的发现吗？

生4：两端物体相同，两种物体个数相差1，两端物体不同，两种物体个数同样多。

4.论证

师：你们有没有想过为什么两端物体相同时，每排两种物体的数量会相差1，又有没有想过为什么两端物体不同时，每排两种物体的数量会同样多呢？这就需要进一步去论证。刚才我们得到的结果只是数出来的，有没有其他办法证明结论就一定是正确的呢？

生5：我们可以一组一组地圈一圈。

师：对，圈也是一种好方法。就请同学们在作业纸上选择一排物体去圈一圈。

师：一组一组地圈一圈，容易发现间隔排列物体间的数量关系。我们可以把这样的过程称之为论证。

【思考：在这个环节中，通过观察图、填表格、摆学具、找规律、想原因，设计了“观察一猜想一验证一反证一论证”这样一个数学思辨的活动探究过程，从根本上改善学生的数学学习方式，促进了数学思考、问题解决、情感态度等方面培养目标的实现，为学生的可持续发展积聚能量。在“观察”中教会学生怎样看，看什么，在数数、填表、比较中得出数量，找到相同点和不同点，从现象中收集数学信息。在“猜一猜”中从事物本质上发现间隔排列物体个数之间的关系。同时，强调了“论证”，让学生夸张地“圈一圈”，意在告诉学生在之前的验证过程中采用的方式都是“数”，运用了某些特例，这只是感性的认识，不足以证明普遍的一般规律，需要进一步的理性的验证甚至是论证，这种方式可以证明一般的规律。】

三、做一做，体验运用，提升学生问题解决能力

【片段三】

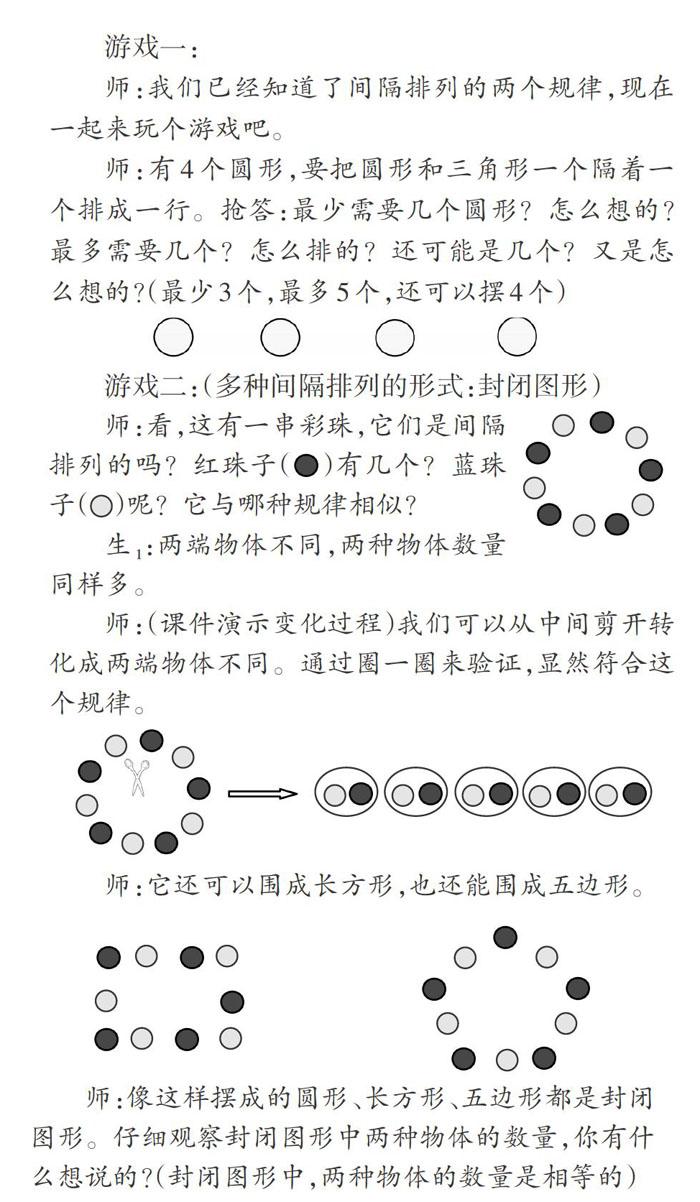
游戏一：

师：我们已经知道了间隔排列的两个规律，现在一起来玩个游戏吧。

师：有4个圆形，要把圆形和三角形一个隔着一个排成一行。抢答：最少需要几个圆形？怎么想的？最多需要几个？怎么排的？还可能是几个？又是怎么想的？（最少3个，最多5个，还可以摆4个）游戏二：（多种间隔排列的形式：封闭图形）

师：看，这有一串彩珠，它们是间隔排列的吗？红珠子（●）有几个？蓝珠子（○）呢？它与哪种规律相似？

生1：两端物体不同，两种物体数量同样多。

师：（课件演示变化过程）我们可以从中间剪开转化成两端物体不同。通过圈一圈来验证，显然符合这个规律。

师：它还可以围成长方形，也还能围成五边形。

师：像这样摆成的圆形、长方形、五边形都是封闭图形。仔细观察封闭图形中两种物体的数量，你有什么想說的？（封闭图形中，两种物体的数量是相等的）

师：仔细观察、认真思考、严格推理，你会发现生活中隐藏着很多规律。

师：今天我们学习了什么？你有什么收获？

师：今天我们从认识什么是间隔排列开始，知道了间隔排列是有特点的，我们还研究了间隔排列的规律和作用。在研究的过程中，我们从观察开始，有了一些发现，我们称之为猜想;然后进行了验证，随即又进行了论证，同时还进行了反证;最后总结了规律.并把这个规律加以运用。这就是我们人类认识未知世界的一种方法！

【思考：好的数学游戏能充分激发学生的好奇心，吸引学生的注意力，发挥学生的想象力。游戏教学中设置一系列问题，让学生自己去思考、去理解、去消化、去吸收，使学生在解决问题的过程中，对知识规律的认识不断加深，体验不断深入，促进学生的思维从碰撞走向融合、从混沌走向清晰，从中进一步感受基本方法和经验，提升数学思考水平。】

苏教版教材的活动课程，紧密围绕“核心素养”，重视两个要素。一是“活”，即方法活，思路活。这是数学思想灵动的表现。二是“动”。活动状态不追求表面的热闹而是追求学生的思考，引导学生的思维向更深处漫溯，引领学生在自主参与中获得充分体验，并将原有的认知进行适当规整与融合，从而建构新的知识系统。这种方法不但解决了数学问题还解决了生活中的问题，培养了学生的数学核心素养。

学生学习数学，获得数学基础知识和基本技能当然是重要的，但不是唯一的。要让学生体会探索规律是数学活动的过程，平时经常使用的数一数、比一比、画一画等方法，都可以应用于探索规律。要让学生体会探索规律需要科学的态度，既要善于观察、大胆猜想，又要及时验证、反证甚至是论证，体会探索规律、发现规律的乐趣，会用数学的眼光看世界，用数学的方法认识客观事物，会通过数学思考去把握千变万化的现象，用数学方法描述、表达变化中的规律。

（责编黄春香）