关于梯形有关概念教材编写及二次开发研究（二）

刘宪升

[摘要]简单梳理“梯形”作为数学名词的来源，并借助梯子的结构，分析了梯形是对其结构（空间）形式和数量关系的本质属性抽象提炼的结果，是人们大脑的反映，展现了梯形有关概念的来源及合理性，水到渠成地得到了梯形的中位线定理，给出了教学中应实现数学知识与生活的有机融合和重视民族语言保护的建议。

[关键词]梯形;梯子;概念;生活

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020）20-0006-03

研究（一）中提到，现行教材中梯形概念的探索活动大多注重与生活的联系，可没有真正触及梯形有关概念来源于生活的本质。那是不是真的可以从生活中抽象、提炼出这种图形为什么叫梯形，为什么只有一组对边平行，为什么上底比下底短等相关知识呢？答案是肯定的。本文就对此做一探讨。

一、数学中“梯形”一词的来源

数学中的梯形在我国古代的数学文献中早已出现，且能计算它的面积，但不是现今的称呼。我国古代数学重视实用，梯形及其面积的求法就是应丈量田地的需要而诞生的。

《九章算术》“方田”章中有“邪田”“箕田”的度量术。其中，“邪田”即斜田，就是现今直角梯形形状的田地;“箕田”就是现今等腰梯形形状的田地。梯形的两底称为舌、踵，高称为正从。但没有出现一般梯形田地的度量，可能是因为它能分成两个直角梯形形状田地的缘故。《五曹算经》中，在继承《九章算术》的基础上又增加了“箫田”的算法，和“邪田”“箕田”并存且算法相同。这里的“箫田”就是一般的梯形（不是等腰梯形和直角梯形）田地。虽然书中未做解释，但因为古代的箫是多管的，形状像鸟翼，鸟翼两侧（相当于梯形两腰）是斜（不与梯形的底垂直）的且不相等，故“箫田”就是指形状像一般梯形的田地。

在徐光启翻译的《几何原本》卷一（四库全书本）中没有“梯形”这个名字，它被归入无法四边形之中。根据法国传教士张诚、白晋从法文译本修订的，收录于《御制数理精蕴》上篇卷二中的《几何原本》（四库全书本）中也没有“梯形”，且据其四边形的分类看不出属于哪一类。

清朝柘城杜知耕撰写的《数学钥》卷一（四库全书本）（http：//www.kanripo.org/text/KR3f0050/001）关于四边形的分类如下：

四速皆等四角中矩者日方形如第一固四角中矩四边雨雨相等者日直形如第二固或四速等或雨速等而四角俱不中矩者日象目形如第三国四速俱不等雨角中矩雨角不中矩者日斜方形如第四固角不中矩雨边相等者日梯形如第五固速及角俱不等者日无法形如第六圖。

其中的“斜方形”就是现今的直角梯形;“梯形”就是现今的等腰梯形。当然，“梯形”作为数学名词，到底第一次是不是出自此书，杜知耕是不是第一个用的人，笔者没有查到。但不管怎样，可以说，第一次在数学上用“梯形”（虽然当时只表示等腰梯形）这个名词的人，是善于观察生活，并能对生活进行抽象和提炼的人，也是发现用“梯形”比用“箕田”更能说明等腰梯形特征的人。因为簸箕底面的形状只是近似等腰梯形（如图1），可以说，用“梯形”更能说明数学中的梯形为什么这么定义，以及为什么上底短、下底长的人，是清楚梯形的中位线定理及其在生活中怎么应用的人。实在令人钦佩！为什么这么说呢？请看下面的分析。

二、数学中梯形有关概念来源于生活

其实，“梯形”作为数学概念来源于梯子的形状，也就是形状像梯子（格）的图形。为解释清楚，有必要对梯子的构造做具体分析。

1.梯子的结构

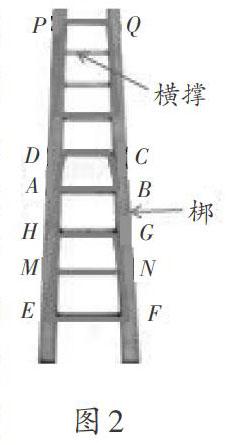
自古以来，梯子就是劳动人民用于上下攀爬的一种常用工具，农村和城镇家庭中几乎都有。只是古代的梯子大都是木质的，现今农村中木质梯子也较多，而城市中金属梯子较多。关于梯子的结构参见木质梯子竖着的图片（如图2）。制作梯子时，一般是用两根比较长且略粗一些的木头（有些直接采用比较合适的两棵树的树干）并排做梆，然后截取若干根适合攀爬的短木头（一样粗细）做横杆——横撑，再将横撑榫卯在两梆之间，制成如图2所示形状。为了安全与方便，梯子的下面宽一些，横撑长一些，两梆也粗一些;往上逐渐缩窄，横撑逐层变短，两梆也逐渐变细。这样制成的梯子重心靠下，将梯子竖起来（下面较宽的一头着地）斜靠在墙上时，不仅省力，因为重心较低，梯子也放得稳当，增加了攀爬的安全性。由于任何两根横撑都是平行的，且相邻两横撑间的距离相等，既方便人们上下攀爬，也提高了安全性。

当然，有些梯子梆的两头一样粗细且两梆平行，有的是為了制作省事，有的是为了实现伸缩功能（伸缩梯子），等等。

2.梯形图形的抽象提炼与有关概念的合理性

据上分析，结合图2可知：梯子的任何两根横撑及其之间的两梆围成的部分（下称“梯子格”），它们的形状都具有两撑平行且之间的两梆不平行的共同特征。若把两根横撑及其之间的两梆抽象成线段，这样的四条线段围成的图形就是数学上的梯形（严格说是等腰梯形），如梯形ABCD、梯形EFGH等。之所以叫梯形是因为图形的形状是梯子格的形状，也可宽泛地说是形状像梯子的图形。这样一来，梯形为什么定义成只有一组对边（代表横撑）平行，而另一组对边（代表两横撑所夹两梆）不平行的四边形就很自然了，因它源于制造梯子时安全与方便的需要。

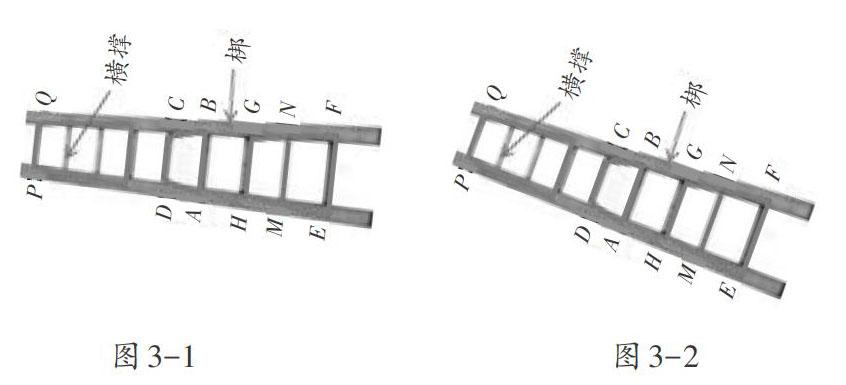
另外，梯形两底中，短的是上底，长的是下底之界定也就符合常识了。因梯子不用时，为了安全和少占用空间，人们将梯子的一梆平放于地斜倚在墙根（另一梆倚墙）（如图3-1），或平放在地上;也有的将较窄的一头的一梆斜靠在比较矮的物体上，如侧立斜倚在墙上（如图3-2），这样再用时竖起来还省功省力一些。甚至为了特殊的需要，人们也可能将梯子较窄的一头朝下竖起来。但不管怎样放置，对梯子来说，哪根横撑在上，哪根横撑在下是不变的。如图3-1、3-2中的横撑AB、DC，DC始终是在AB上面的一根横撑，AB始终是在CD下面的一根横撑，不因梯子摆放位置的不同而改变。这就是数学中规定梯形的两底中较长的底是下底，较短的底是上底的原因。因为根据梯子的结构，上面的横撑比下面的横撑短。