把握面积计算的本质

胡利群

[摘要]当前小学数学课堂在核心素养理念的引领下，正从以往更多关注学生对知识的理解与掌握，转向如今关注于学生的数学学习能力、数学技能与思想等方面。对一次全国性观摩活动中“长方形和正方形面积的计算”教学出现的问题进行剖析，并依托网络教室，抓住面积的本质，引领学生进行了“摆、量、估、议”四个层次的活动教学。

[关键词]长方形和正方形;面积计算;本质;案例

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020） 20-0019-03

【案例】

在一次全国性观摩活动中，一位教师执教“长方形和正方形面积的计算”时，以“实验一猜想一验证一概括”为探究主线，以期让学生掌握这两种图形的面积计算方法的同时能获得一种科学的研究问题的方法。

实验中，学生用12个边长为1分米的正方形摆长方形，三种摆法得出三组数据“4分米、3分米、12平方分米;6分米、2分米、12平方分米;12分米、1分米、12平方分米”，教师（将长方形搁置一边）引导学生分析这几组数据，发现长与宽相乘的积与长方形的面积正好是相等的，由此得到一个猜想（公式），继而举例验证：先用公式计算，再用面积单位测量，发现两种方法得到的答案是完全一样的，最终概括得出长方形面积计算的公式。接着给出3道练习题，都是根据图形上标出的长与宽直接口答出图形的面积，其中有一个是边长为6厘米的正方形（标出了两条邻边），学生出于惯性的回答没有出现任何问题，然而由此提升总结正方形面积公式时，学生却“呼之不出”：有的说是“边长x4”，有的说是“边长x6”，无法实现由长方形面积公式到正方形面积公式的迁移。

【剖析】

诚然，个别学生误将正方形的周长公式用于此也无可厚非，因为周长和面积毕竟是两个非常容易混淆的概念，但全班学生“万马齐喑”就不对劲了。

仔细揣摩整个公式的探究过程，教师是在引导学生从纯数据的角度找规律，即长乘宽恰好等于面积（而面积是用面积单位测量出来的）。我以为，仅从数据分析的角度来探索长方形面积的计算公式有点不妥，在“猜想、验证”的背后是否还差一个“沟通、解释”？因为学生心中可能会有一个大大的问号——为什么长乘宽正好等于面积呢？教师在长方形面积计算公式推导的过程中一直浮于数据相等的表面，没有引导学生体会长方形面积计算的本质，在摆、量的过程中体会长方形的长、宽与面积单位个数之间的对应关系，所以学生没有形成一定的方法，无法迁移可能是因为无“法”可移。

实际上，用面积单位测量面积的方法是探究面积计算公式的基础。一个图形面积的大小本质上是它所含相同面积单位的多少（这是在认识面积单位时学生就已经掌握的），所以计算图形的面积实际上就是在计算面积单位的个数，即每排的个数乘排数（这是二年级“认识乘法”的内容），可以说这两点对于学生来说都不是难点，难点在哪里呢？在于引导学生意识到长方形的长、宽或正方形的边长与每排个数、排数之间的关系，即每排的个数和排数是由长方形或正方形的两条邻边决定的，这一点是得出长方形面积计算公式的关键所在，也是沟通长方形和正方形面积计算公式的桥梁，在教学中应重点引导学生打通这一“关节”。

基于以上思考，我对本课进行了一次教学（苏教版教材三年级下册第82、83页），并将课堂“搬”到了电脑教室。

【实践】

活动一：摆

师：请在电脑上用若干个1平方厘米的正方形摆一个长方形或正方形。

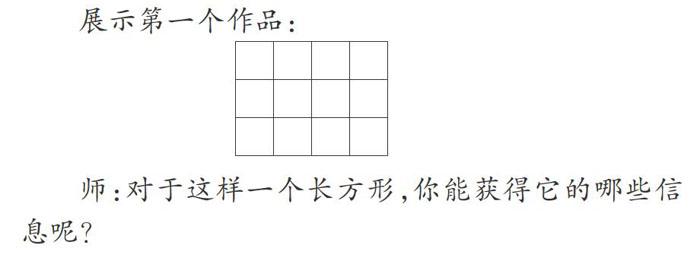
展示第一个作品：

师：对于这样一个长方形，你能获得它的哪些信息呢？

生1：它的长是4厘米，宽是3厘米。

师：怎么看出来的？

生1：因为一排摆了4个正方形，每个正方形的边长是1厘米，所以长是4厘米.摆了3排，所以宽是3厘米。

生2：它的面积是12平方厘米。

师：怎么知道的？

生2：因为用了12個1平方厘米的正方形。

师：“12个”是你一个一个数出来的吗？

生2：不是，是算出来的。每排4个，有3排，就是4x3等于12。

师：这是一道简单的乘法算式，对吗？瞧，我们在二年级学习的几个几是多少在这里又用上了。

师：还有谁想展示？在展示之前想一想，怎样介绍让别人还没看到就已经能想到它的样子。

生3：我摆了三排，每排摆3个小正方形。

师：能想象她摆的图形是什么样的吗？

生4：她摆的是一个正方形，边长是3厘米。

展示生，作品：

师：看来摆正方形时有个特点。

生5：边长都是一样的。

生6：排数和每排的个数是一样的。

师：那这个正方形的面积是多少呢？

生7：9平方厘米，3x3=9。

师：又是一道乘法算式，两个“3”的意义一样吗？

（展示第三个作品;略）

师：通过刚才的摆，我们发现看一个图形的面积是多少其实就是看什么？（板书：面积单位的个数）小正方形的个数是一个一个数出来的吗？怎样算？（板书：每排个数×排数）

活动二：量

师：用一些1平方厘米的正方形量出长方形的面积。（学生在电脑上操作，完成后交流）

展示第一种方法：

师：面积量出来了吗？说说你的想法。

生1：每排5个，摆了4排，共有20个1平方厘米的小正方形，面积是20平方厘米。

师：其实他不仅量出了长方形的面积，他还量出了长方形的——

生2：长是5厘米，宽是4厘米。

展示第二种方法：

师：这样摆可以吗？他都没摆满，为什么也可以？

生3：因为这样能看出一排有几个且有几排。

师：这样就可以用一道乘法算式得到一共要多少个正方形。能看出长与宽吗？比较一下，两种量法你更欣赏哪一种？

活動三：估

师（出示一个长方形）：这里有一个长方形，估计一下它的面积是多少，说说你是怎样估计的，怎样知道估得准不准呢？

生1：用1平方厘米的小正方形去量。

师：只能用小正方形去量吗？还可以用什么量？

师（出示：长6厘米）：你能想到什么？

生2：一排能摆6个小正方形。

师：如果长是5厘米呢？7厘米呢？16厘米呢？也就是说——

生3：长是几厘米，一排就能摆几个小正方形。

师：看来长方形的长决定了一排能摆几个面积单位。只知道这一个条件就行了吗？

生4：还要知道摆几排。

师（出示：宽3厘米）：现在知道能摆几排了吗？（演示课件验证）能用一道乘法算式表示它的面积吗？

师：这里有一个正方形，估一估它的面积是多少。这回你需要几个条件？为什么？

活动四：议

师：学到这里，大家可能已经知道了这节课我们学习的内容是什么了。（板书课题）那长方形的面积和什么有关呢？怎样求长方形的面积？正方形呢？在小组内交流自己的看法。

（教师板书两个公式。两个公式的得出非常轻松，一方面可能是前面的铺垫比较到位，另一方面，即使没学今天的课，不少学生也已经知道这两个公式了，所以下面这个环节很重要）

师：能具体地解释一下这个公式吗？长指的是

生1：每排能摆几个。

师：宽呢？

生2：能摆几排。

师：这个“边长”指的是……那另一个“边长”呢？这两个公式有什么相同的地方吗？

生3：它们都是在求有多少个小正方形（面积单位）。

生4：它们都是邻边相乘。（这位学生的发言可谓是石破天惊）

师（将两个公式合为一体，板书：邻边相乘）：可见长方形和正方形面积的计算并不神秘，就是我们在二年级学习的“几个几是多少”的应用而已。

【反思】

一、依托网络教室，提高教学效率

本节课在网络教室进行绝非为了哗众取宠。之所以不放在教室，是因为学生的摆、量都不便于在全班展示;之所以不放在报告厅，是因为图形投影到大屏幕上之后，面积放大了若干倍，不利于学生建立面积大小的正确表象，尤其是估计长方形面积环节，直接影响着学生估计的结果。实践证明，学生在操作电脑时用鼠标拖动小正方形来摆、量都非常方便，速度远远高于实物操作，并且在局域网中能任意展示学生的作品，这样不仅极大提高了教学的效率，同时这种新颖的教学方式也激发了学生的参与热情。

二、抓住一个重点，推进四次活动

这节课的重中之重是让学生认识到长方形、正方形的邻边与排数、每排个数之间的关系，围绕这一点，我引领学生进行了“摆、量、估、议”四个层次的活动。

“摆”，学生最容易关注到的往往是用了多少个正方形以及每排摆几个、摆了几排。我通过一句“对于这样一个长方形，你能获得它的哪些信息呢？”将学生的目光从单个的正方形吸引到长方形上来，学生自然也就能够关注到长方形的长、宽与面积了。

“量”，学生最关心的是量的结果，即它的面积是多少，因为操作的要求就是测量图形的面积。算式中的两个乘数，学生仅仅把它看作“个数”与“排数”而已。“其实他不仅量出了长方形的面积，还量出了长方形的——”一句启发性的话让学生将“个数、排数”与“长、宽”联系起来。

“估”，一方面，通过学生有没有用估的方法可以检验出“每排个数×排数”是否已深入学生的大脑，另一方面，前两个环节是由“个数”想到“长、宽”，而这时出示“长”，问学生“能想到什么”，则是引导学生由“长”联想到“个数”，这一恰好相反的心理活动让学生进一步深入认识了它们之间的关系。

“议”，重点同样是放在了对公式的理解上。这一活动是对前面几个环节的总结与提升，如果说前三个活动是在挖渠，那么这个活动则是渠成之后的涓涓清流。

三、淡化图形区别，把握计算本质

从本质上来说，长方形和正方形的面积计算方法是完全一样的，所以在以往的教学中，一般都是先推导长方形面积的计算公式，再将其迁移到正方形面积的计算公式。而我在教学中有意淡化两种图形的区别，不分彼此，同步进行它们面积公式的推导，以期能够引导学生真正体会面积计算的本质所在。在第一个环节，主要让学生感觉到正方形摆的时候有点特殊，却和长方形一样都可以用一道简单的乘法算式得到面积单位的个数，并且让学生注意到乘法算式中的两个数虽然相同，但意义不一样。在估正方形的面积时让学生说一说需要几个条件，再次让学生注意到正方形与长方形的面积计算是相同的，两个乘数的意义是不一样的。最后的“议”着重引导学生关注两个计算公式有什么相同的地方，学生的那句“它们都是邻边相乘”可谓是字字千金，这也正是教师苦心经营所期望实现的目标。

综上，同样的教学内容之所以有不同的教学设计，绝非为了标新立异刻意为之，而是不同的教学思考在教学形式上的具体体现。形式是为内容服务的，教什么比怎么教更重要！

（责编金铃）