例谈数学思想方法的渗透

李利君

[摘 要]数学课堂中，教师不仅要关注学生习得数学知识的情况，还要从知识形成、探究活动、解决问题、复习整理等方面渗透数学思想方法，使学生真正理解和掌握所学的数学知识，提升学生的数学核心素养。

[关键词]小学数学;思想方法;渗透

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）15-0021-02

数学课堂中，教师注重渗透数学思想方法，可以使学生更好地理解数学知识的本质，提升学生的数学核心素养。那么，怎样才能揭示蕴含在数学知识中的数学思想方法，并在教学中有效渗透呢？教师应根据具体的教学内容，抓住渗透数学思想方法的时机，引导学生经历数学思考、操作探究的过程，使学生感悟其中的数学思想方法，真正理解和掌握所学的数学知识。

一、在知识形成中渗透数学思想方法

数学知识产生、发展与形成的过程，其实也是学生形成数学思想方法的过程。数学课堂中，教师应从学生的认知规律和具体的教学内容出发，尽可能地为学生提供丰富的、典型的、直观的学习材料，引导学生经历建立模型到应用拓展的过程，使学生感悟其中的数学思想方法，提升数学课堂教学质量。

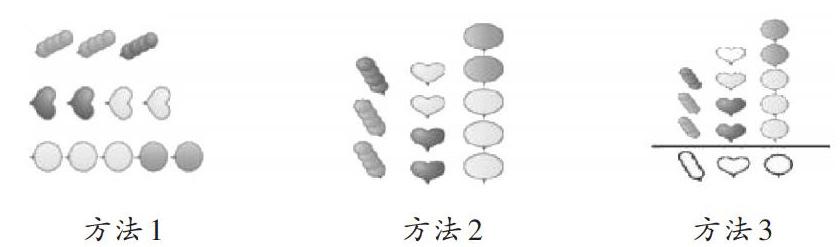
例如，教学《分类》这一内容时，教师借助多媒体课件呈现气球图，让学生说说怎样把这些气球进行分类。一学生说：“可以将气球按不同的形状分类，如心形的、糖葫芦形的以及圆形的。”教师对学生的分类方法表示肯定，然后让学生拿出学具亲自分一分并交流汇报。如下：

[方法1][方法3][方法2]

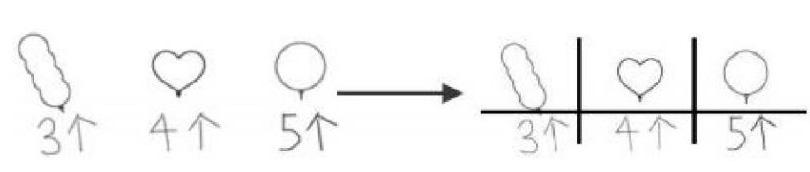
接着，教师让学生说说分类有什么好处，有学生说“分类后可以一下子看到每种形状的气球各有几个”。顺着学生的思维，教师追问：“是不是哪种气球摆放越长，就说明这种气球越多呢？你还有能够准确标记出每种形状的气球各有多少个的方法吗？”在学生总结出方法后，教师出示下图并提问：“这里，左边是同学自己画的图，右边是老师加了竖线的图，你们觉得哪种方法表示得更清楚呢？”学生齐声回答：“右边的图表示得更清楚。”……这样教学，学生亲历了知识的产生和形成过程，体验更加深刻。这里，教师创设动手操作的教学情境，不仅为学生今后学习统计的知识奠定基础，而且有机渗透了分类中的一一对应思想，可谓一举多得。

二、在探究活动中渗透数学思想方法

探究是一种有效的学习方式，且小学生的思维正处于从形象思维向抽象思维发展的过渡时期。因此，数学课堂中，教师要善于引领学生深入探究，使学生在观察、操作以及思考交流的活动中获得新知，感悟其中的数学思想方法。

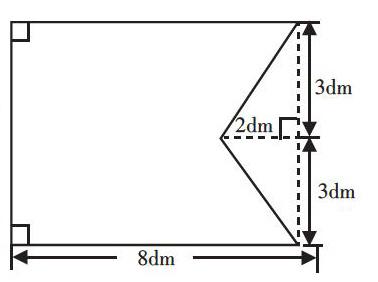
例如，教学《组合图形的面积》时，由于这一内容是在学生已学基本图形面积计算的基础上学习的，所以教师通过探究活动渗透转化的思想方法。课始，教师提问：“学校打算制作一面中国少年先锋队队旗，你能估计出它的大概面积是多少吗？”学生观察图后，认为这面队旗的面积大概在36平方分米至48平方分米之间。对于学生的回答，教师追问道：“能说说你的理由吗？”在讨论交流中，学生认为可以用添加辅助线的方法把不规则图形转化成规则的图形（如右），这样解决问题就简单多了。教师给予肯定后启发学生继续探究：“那么，怎样才能求出这面队旗的面积？能用哪些方法来解决问题？”有的学生说，可以把队旗的面积看作两个梯形的面积;有的学生认为，可以用长方形面积减去三角形的面积;有的学生则认为，可以采用正方形面积加三角形面积的方法求解……为了使学生对转化的思想方法有更深刻的认识，教师鼓励学生对提出的各种方法分类，如分割法、添补法等。最后，教师让学生找出这些方法的共同点，使学生明白不管采取什么方法，其目的都是为了把不规则图形转化为规则的图形，从而有效地渗透了转化的思想方法。由此可见，在图形面积计算的教学中，教师要鼓励学生独立探究解决问题的方法，并有机渗透转化等思想方法，使学生获得深刻认知。

三、在解决问题中渗透数学思想方法

解决问题是小学数学教学内容的重要组成部分。要想解决问题，学生不仅要真正理解所学的数学知识，还要掌握一定的数学思想方法。因此，在數学课堂中，教师可借助解决问题对学生进行数学思想方法的渗透，促进学生数学思维的发展。

例如，有这样一道题：“一杯牛奶，小芳第一次喝了半杯，第二次喝了余下的半杯。就这样，她每次喝的都是余下的一半，你知道她5次一共喝了多少牛奶吗？”学生大都采取[12+14+18+116+132]的方法求解，但这并不是解决问题的唯一方法。教师可引导学生采取画图的方法来解决问题：“我们先画一个正方形，然后以这个正方形为单位‘1……”借助形象直观的图示，使学生明白[1-132]就是所求问题的答案。这样教学，于无形中对学生进行了数形结合以及类比思想的渗透，收到了好的教学效果。因此，在教学解决问题时，教师不仅要关注学生的学习结果，还要注重对学生进行数学思想方法的渗透，提升学生的数学学习能力。

四、在复习整理中渗透数学思想方法

复习是一种有效的学习方法，可以促进学生对所学知识的吸收、内化与运用。因此，在学生学习一个章节内容或一个板块内容之后，教师可从数学思想方法的角度引领学生对所学知识进行整理与概括，提升学生的数学学习质量。

例如，教学《运算定律的整理与复习》时，教师鼓励学生把自己学到的知识说一说，要求着重把“学了什么”和“学到什么”说清楚。学生回答时总是习惯照搬书上的理论概述，这时教师可启发学生：“除了用文字表述外，我们还可以采取哪些方式来表示学过的运算定律？”学生根据已有的知识经验，认为还可以用图形、符号等来表示运算定律。然后教师通过多媒体出示图片，让学生观察后说说每幅图表示的是什么运算定律。在分析与表达的过程中，学生对于用图形来表示运算定律有了进一步的认识。最后，教师引导学生对本单元的知识进行梳理，使分类这一思想方法得到了有效的渗透。同时，教师提问：“加法交换律与乘法交换律之间有什么相似之处？加法结合律和乘法结合律呢？”……这样教学，有机渗透了符号、对比、数形结合等思想方法，收到了显著的教学效果。因此，在复习教学中，教师根据教学内容对学生进行数学思想方法的渗透，可以帮助学生建构完整的知识体系，使学生体会到数学思想方法的运用价值。

综上所述，数学思想方法不仅是解决数学问题的灵魂，而且是数学学科的精髓与核心。因此，教师要充分认识到数学思想方法的意义和价值，善于抓住课堂教学中恰当的时机，对学生进行数学思想方法的渗透，帮助学生真正把知识转化成能力，提升学生的数学核心素养。

（责编 杜 华）