基于概念图的中外高中数学教材比较研究——以澳大利亚、美国、英国和中国教材中矩阵内容为例

胡典顺，王春静，王 静

基于概念图的中外高中数学教材比较研究——以澳大利亚、美国、英国和中国教材中矩阵内容为例

胡典顺1，王春静2，王 静3

（1．华中师范大学 数学与统计学学院，湖北 武汉 430079；2．天津市双桥中学，天津 300350；3．宜春外国语学校，江西 宜春 336000）

概念图既呈现了其中的每个核心概念的纵向发展主线，又显示了概念之间的横向联系，是组织和表征知识的有效工具．以概念图为研究工具，选取澳大利亚、美国、英国和中国具有代表性的高中数学教材，深入探讨、比较4国教材中矩阵内容的概念，并制作相关概念图，研究矩阵内容在4国教材中的广度和深度．发现美国和中国教材无论在广度和深度上都比英国和澳大利亚教材更占优势．对中国高中数学矩阵内容的教材编写提出以下几点建议：保持优势，重视“双基”；广度和深度相适宜；合理运用信息技术；完善高中矩阵内容的知识结构．

概念图；矩阵；高中数学教材；中外比较研究

1 问题提出

数学概念是人们对现实世界空间形式和数量关系的概括反映，是建立数学法则、公式、定理的基础，也是运算、推理、判断和证明的基石，更是数学思维、交流的工具[1]．根据定义，数学概念具有概括性、抽象性，是数学学习的基础，只有正确理解数学概念，才能深刻理解数学的本质．数学概念的学习对学生来说有时是抽象难懂的，数学中又有很多数学概念，为了让学生更好地理解数学概念及数学概念之间的联系，可以使用概念图来帮助学生形象直观地构建知识、加深理解．概念图是诺瓦克教授等人于20世纪60年代根据奥苏贝尔的有意义学习理论提出的一种教学技术[2]．概念图是用来组织和表征知识的工具，具有思维可视化特征，能够提供清晰的组织结构以促进学习者从知识的整体结构中寻找所需的学习资源．

作者在美国访学和研修期间，发现当地高中二年级学生能够熟练地运用矩阵解线性方程组，用科学计算器和矩阵知识配平复杂的化学方程式．同时，在很多国家，比如澳大利亚和英国，矩阵知识都是高中数学的必修内容．但在中国高中数学课程中，矩阵知识属于选修内容，并且由于高考的压力，很多地区和学校没有选修该部分内容．尽管在高中阶段开设与矩阵相关的课程具有一定的可行性，但鉴于国内外的教材与教学中对矩阵内容的安排差异比较大，这里以概念图为研究工具，选取澳大利亚、美国、英国和中国4国具有代表性的高中数学教材，深入探讨、比较4国教材中矩阵内容的概念，并制作相关概念图，研究矩阵内容在4国教材中的广度和深度．以期对国内外高中数学教材中矩阵内容安排的可行性作进一步分析，为教材中矩阵内容的编写提出一点建议，通过概念图来帮助中国中学生更好地掌握矩阵这一研究数学的工具．

2 研究概述

近年来，不同学者从不同角度进行了初高中数学教材的国际比较，取得了不少成果[3-7]．以概念图为视角，相关学者也进行了一些研究[8]．按照诺瓦克教授所描述的，概念图通常将与某一主题有关的概念置于圆圈或方框之中，然后用连线将相关的概念连接起来，连线上标明两个概念之间的意义关系．概念图通常包括节点、连线、连接词、命题和层级等基本要素，其中，节点表示概念；连线表示概念之间的意义联系，并用箭头表示方向，交叉连接是概念图中两个有关系的模块之间的连接；连接词是在连线上用于表明两个概念之间关系的字、词、符号或短语；命题是两个概念之间通过连线、连接词而形成的概念、原理的更深层意义关系；层级是同一知识领域中的概念依据其概括水平不同所进行的分层排布，概括性最强、最一般的概念处于图的最上层，从属的概念放在其下[9]．概念图既呈现了其中的每个核心概念的纵向发展主线，又显示了概念之间的横向联系，每个概念图都是一个主线明确、联系通道顺畅的网状体系．国外对概念图的研究比较前沿、规范，在概念图的基本结构、特征、分类、编制过程、应用、评价标准等方面的研究较为深入[10]．如，Cheng C W、Greg C L和Huang K L对如何运用概念图进行教学进行了深入阐述[11]；Stoyanova N和Kommers P认为概念图可以作为合作学习的工具，基于计算机的概念图可以分享不同学习者的认知情形[12]，等等．国外对概念图的研究特点主要表现为：在教学中，从评价工具发展成为教学技能及策略；在绘制中，由手工发展成为软件制作；在应用中，由科学学科向其它学科和社会应用发展．

概念图的研究从20世纪90年代末传入中国，起步较晚．近些年来，与概念图相关的研究成果也越来越多．章建跃等人通过研究表明：美国、法国、德国、日本等国教材十分重视发挥核心概念的育人功能，围绕核心概念建立教材的结构体系[13]．美国高中数学课程和UCSMP教材在代数领域、几何领域以及数据统计与概率领域的核心概念处理上都有鲜明特色[14]．张豪锋、赵耀远、吴金鸽对多维概念图的应用进行了研究[15]．梁荣荣、何秀玲等论述了面向课堂教学的概念图自动生成方法[16]．解加平、辛涛对概念图中学生的评估体系做了研究[17]，等等．

概念图最初主要是作为检验学生知识结构的一种评价工具，但随着相关研究的不断深入，其应用范围发生了很大的变化，在科研、教学、生物医学、企业的知识学习等方面都有应用．在教育教学方面，概念图在合作学习、探究式学习、移动学习资源设计等中的作用也很大，可以用于教学设计、新课导入、教学评价、复习小结中，有助于教师整体把握知识框架与教学思路、促进教学反思，能够促进学生更好地掌握知识结构．概念图在教育中的研究大多数是基于教学的视角，强调在教学中的用途，对教材的深入研究比较少；此外，定性研究比较多，定量研究比较少．国际数学教育的比较研究是数学教育领域的重要研究主题，这里以概念图为视角对中外教材进行比较分析．

3 研究设计

3.1 研究对象

为了使研究的结果具有代表性和推广性，需要选择在各个国家广泛使用的教材．因此，选择了澳大利亚VCE版本、美国Glencoe的代数2、英国A-Level版本进阶数学（高等数学）中的和中国人教版普通高中实验教科书选修4-2“矩阵与变换”作为研究对象，选取其中与矩阵有关的内容，比较4国教材在矩阵中的广度和深度，并进行相关统计分析，各国教材版本具体信息如表1所示．

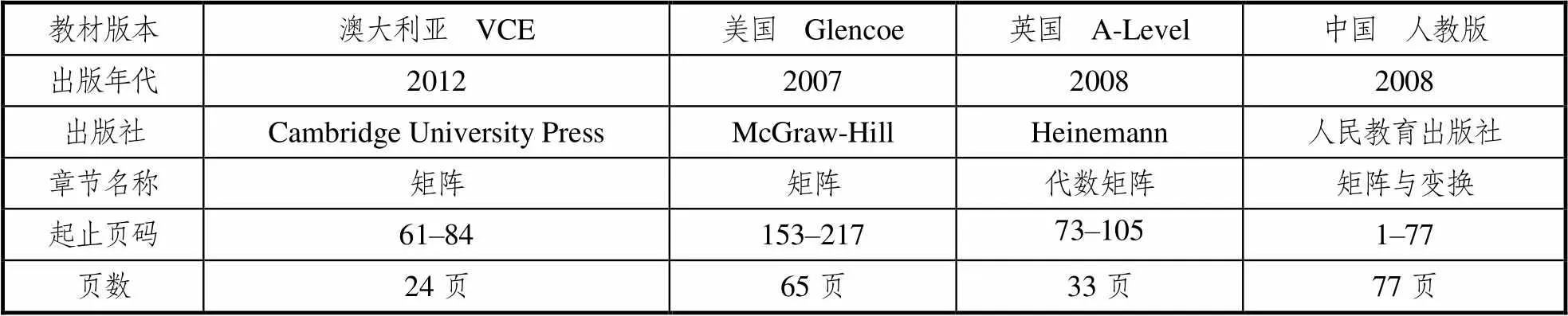
表1 各国教材版本信息

3.2 研究工具

以概念图为研究工具，基本思路是用节点表示概念，用连线表示概念之间的联系．用Cmaptools软件制作4国教材中矩阵知识的概念图，具体步骤如下：分别选取4国教材中矩阵的基本知识及概念作为概念图的节点；根据概念的不同概括水平确定概念的层级，从上位到下位进行分层；用连线把同一模块中的概念连接起来或对不同模块中的概念进行交叉连接．在绘制概念图的过程中，列举出所有与矩阵相关概念之后，就可以根据概念的数量分别计算4国教材中矩阵的广度；概念图绘制完成之后，再对矩阵的深度进行分析．

3.3 研究方法

首先，分别统计4国教材中所有的矩阵相关概念，去掉重复出现的，最后得到的概念总数算作是4国教材矩阵的总概念数；再分别计算4国教材涉及的概念数在总概念数中所占的百分比，定性、定量地比较分析4国高中数学教材矩阵内容的数学知识广度．

其次，先分模块，主要用最长连接长度和连接的总和来衡量各国教材的深度，再综合比较．将连接中的一个节点计为一个单位，连接的长度即连接的节点的个数．在计算连接的长度时，规定以下两点：（1）交叉连接归为连接，即在计算连接长度过程中，若出现交叉连接，则计入该连接中，但不再将交叉连接后面的节点计入该连接中．（2）计算连接长度时，每个节点在一个连接中只计算一次，并取最长连接的长度作为连接长度．连接最长长度即在所有连接中连接节点数量最多的连接的长度；连接的总和是由各个连接的长度与该长度连接数量的乘积相加得到．

4 研究结果

4.1 矩阵内容广度的比较结果

根据4国教材中矩阵的概念清单计算出该国的概念数与总概念数的比值，4国教材中矩阵内容的数学知识广度比较的柱形图如图1所示．

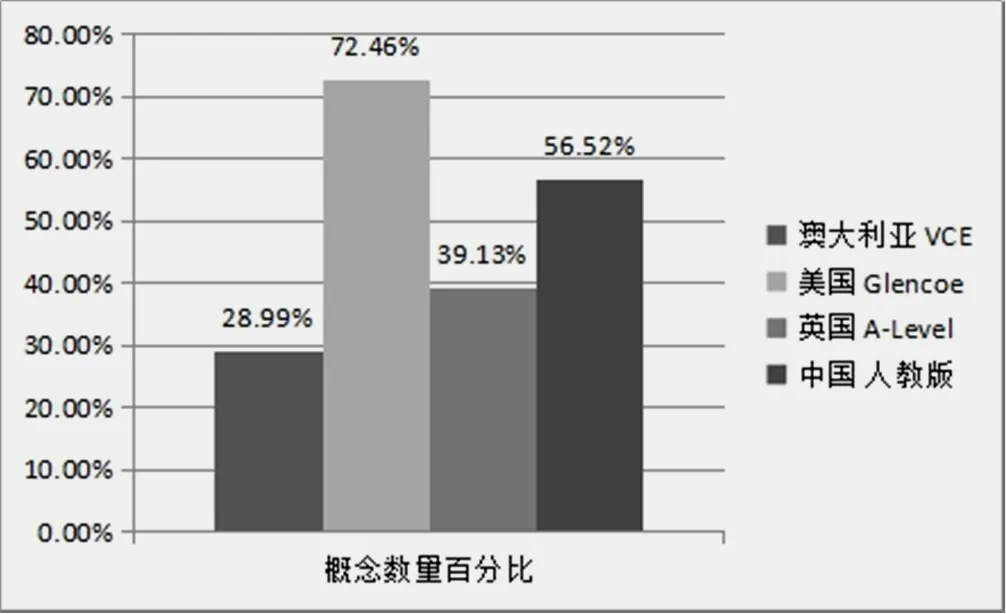
图1 4国教材中的矩阵内容的数学知识广度比较

4个国家高中数学教材中一共涉及69个与矩阵相关的概念．其中，美国教材中包含的概念最多，有50个，占72.46%；其次，中国有39个与矩阵相关的概念，占56.52%；英国教材中包含的概念数少一些，有27个，占39.13%；澳大利亚教材中包含的概念数最少，只有20个，占28.99%．由此可以看出，美国教材广度最大，中国次之，英国和澳大利亚的教材中矩阵部分的知识点广度相比其他两个国家差距略大，美国高中数学中与矩阵相关的概念数量是澳大利亚的两倍多．4个国家教材有很多相同的概念，比如矩阵的元素、单位矩阵、零矩阵、逆矩阵、矩阵的乘法等，但在不同教材中各有特色．

美国教材有17个概念是其他国家没有的，与其他国家相比较，涉及了阶矩阵、三阶矩阵、余子式等；在矩阵的乘法分配律中，不仅包含了数乘矩阵的分配律，也包含了矩阵相乘的分配律，又将矩阵乘法的分配律分为左乘和右乘．中国教材中共有12个矩阵相关概念是其他国家没有的，比如：特征向量、特征值、特征行列式、二阶矩阵的方幂、投影变换、切变变换、二元一次方程有非零解等，教材以具体图形的变换为起点来认识矩阵这一数学工具，注重数和形的结合，通过图形变换认识矩阵，再以矩阵为工具用代数的方法表示图形的变换．英国教材只有一个概念是其他国家没有的——方位矩阵，用方位矩阵表示变换前后的图形以方便研究，这与英国教材中注重将图形变换与矩阵及其运算结合起来有关系．澳大利亚教材中所有概念都在其他国家教材中出现过而且比较简单．

4.2 矩阵内容深度的比较结果

概念图的制作没有固定的模式，这里按照以下4个步骤完成概念图的制作：列出关键概念清单；确定概念等级；初步制作概念图，建立层级；不断修改，逐步完善．利用Cmaptools软件制作的4国教材中矩阵知识的概念图，分别如图2、图3、图4和图5．

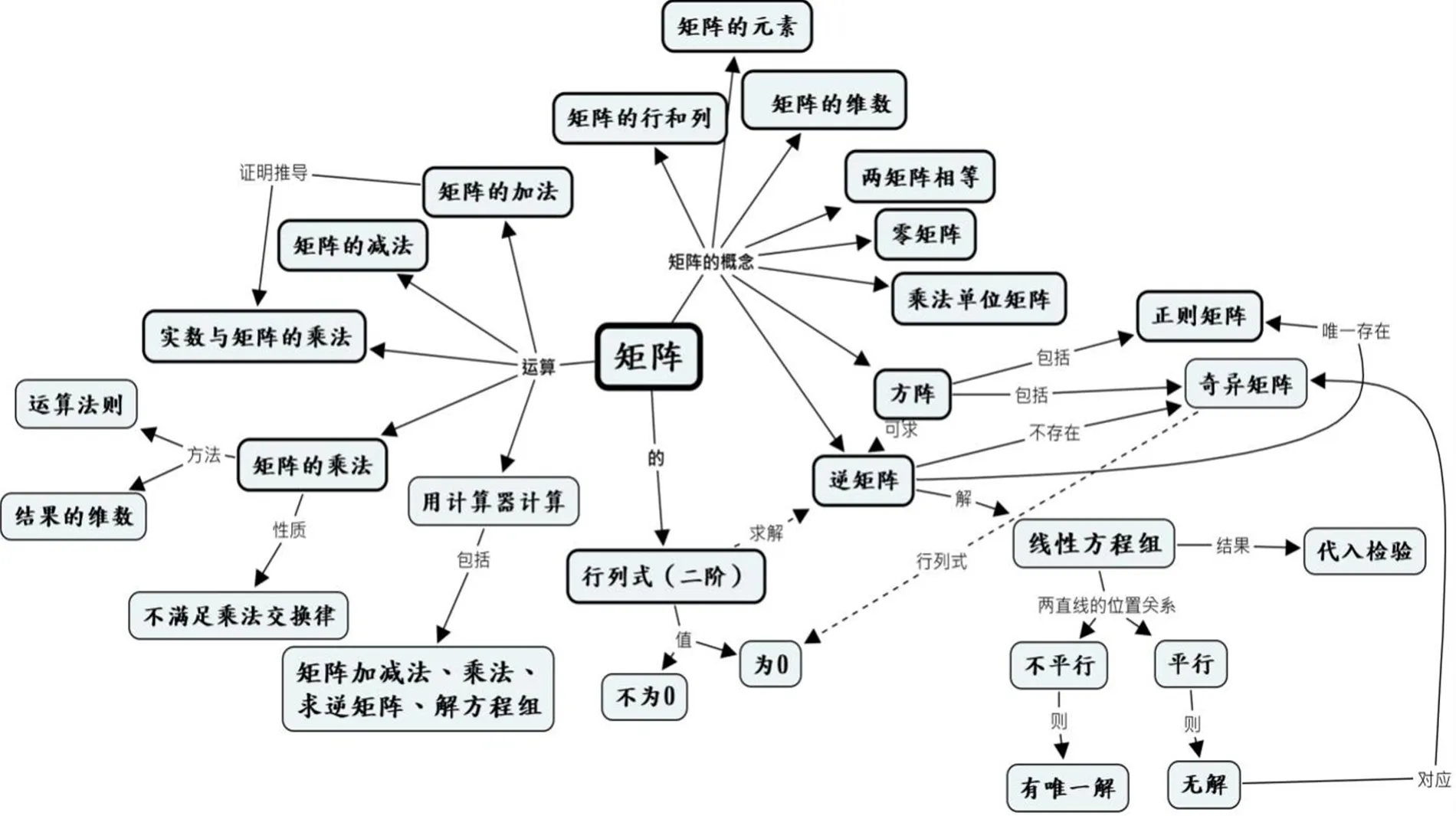
图2 澳大利亚教材概念

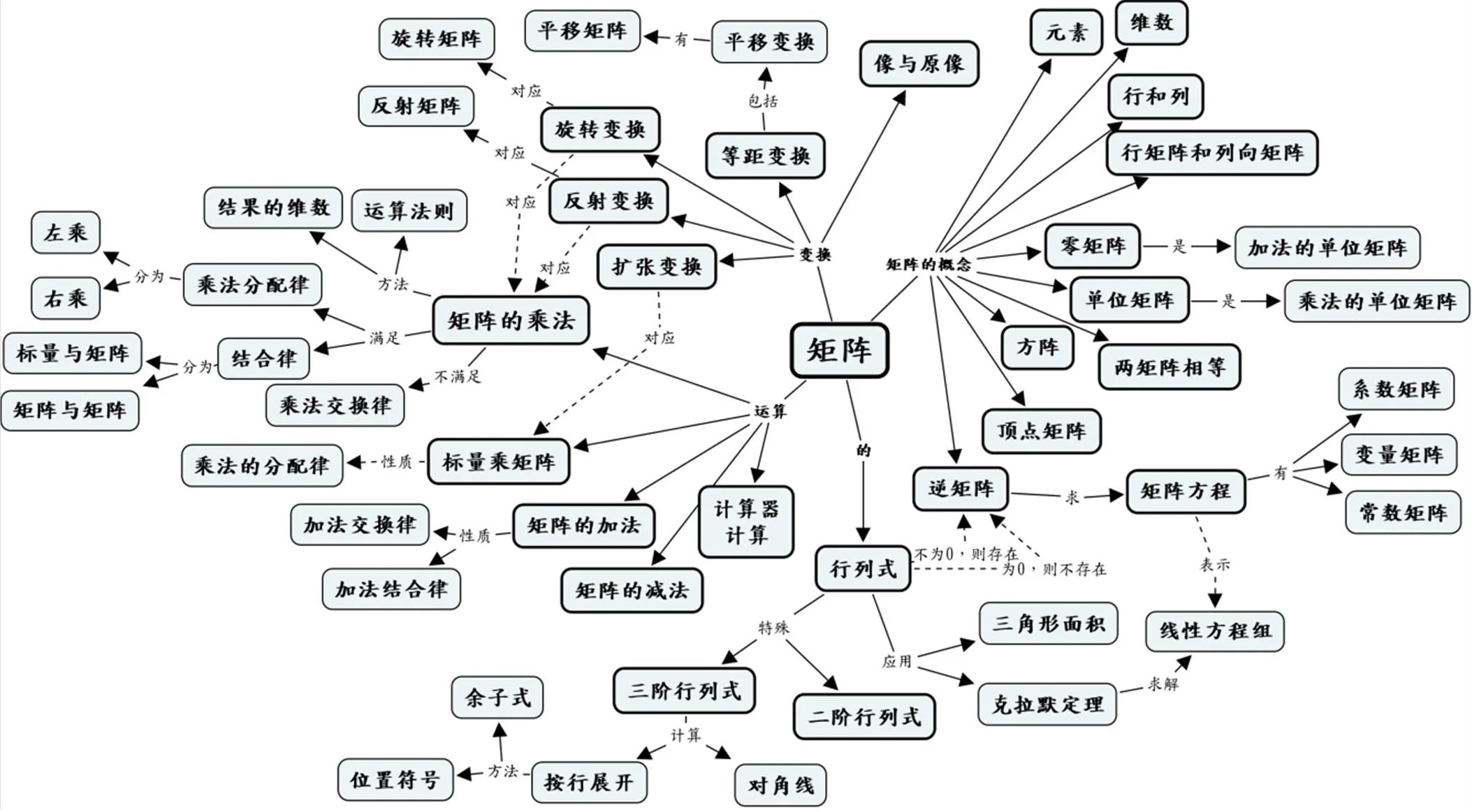
图3 美国教材概念

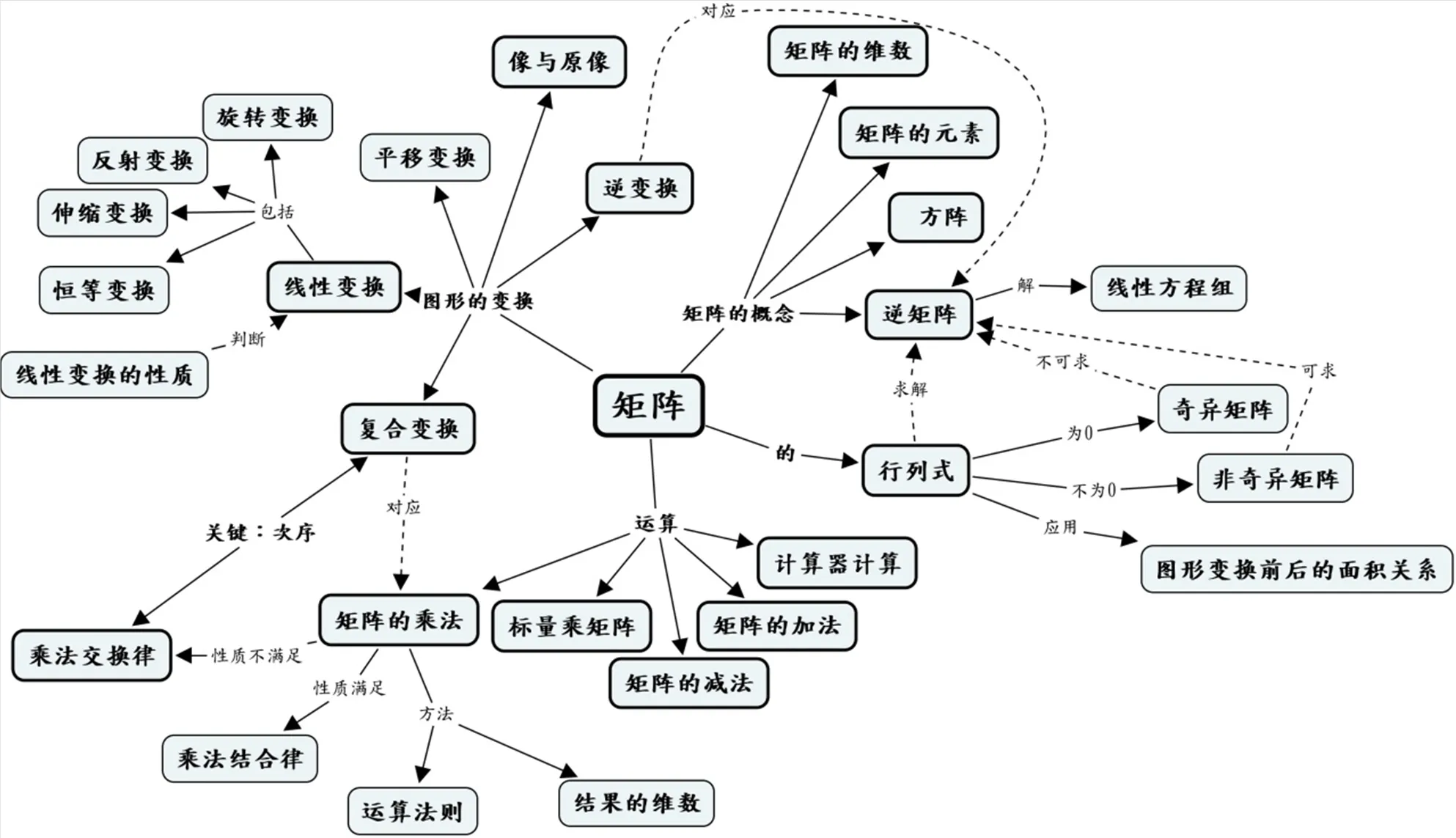
图4 英国教材概念

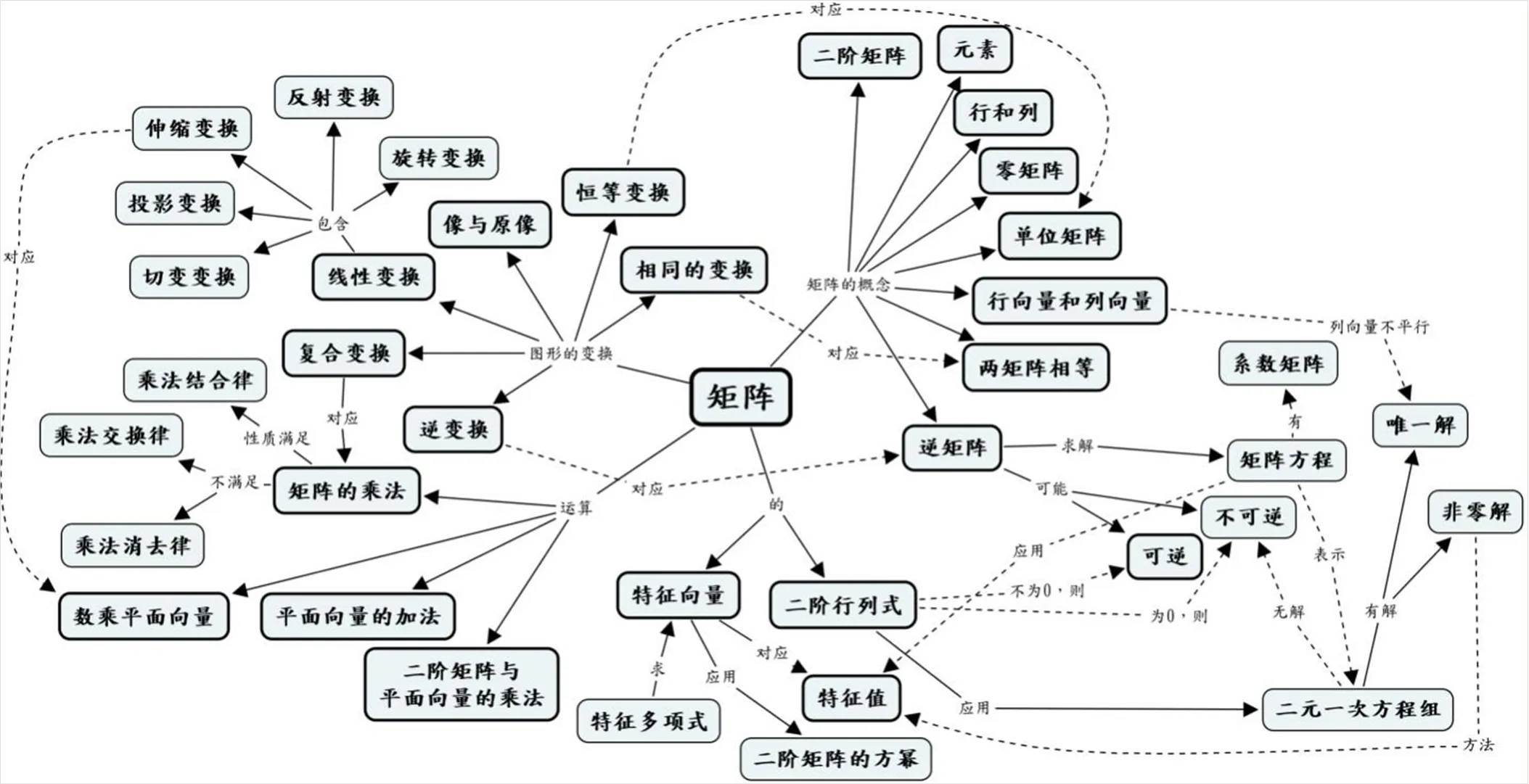
图5 中国教材概念

比较4个概念图连接以及交叉连接的数量和拓展的程度，可以发现澳大利亚和英国教材的概念图比较简单，而中国和美国的概念图比较复杂．主要用最长连接长度和连接的总和来衡量各国教材的深度，连接的最长长度越长，表示在一定程度上深度越大；连接的总和越大，可在一定程度上说明深度越大．仔细观察这4个纵横交错的概念图，发现除澳大利亚教材外，其他每个国家教材中都涉及了与“图形的变换”有关的概念．第一层次有4个明显的节点——“矩阵的概念”“矩阵的运算”“图形的变换”“行列式及其它”．下面从这4个模块分别比较4国教材中矩阵内容数学知识的深度．

（1）矩阵的概念．

4国“矩阵的概念”模块深度对比见表2．

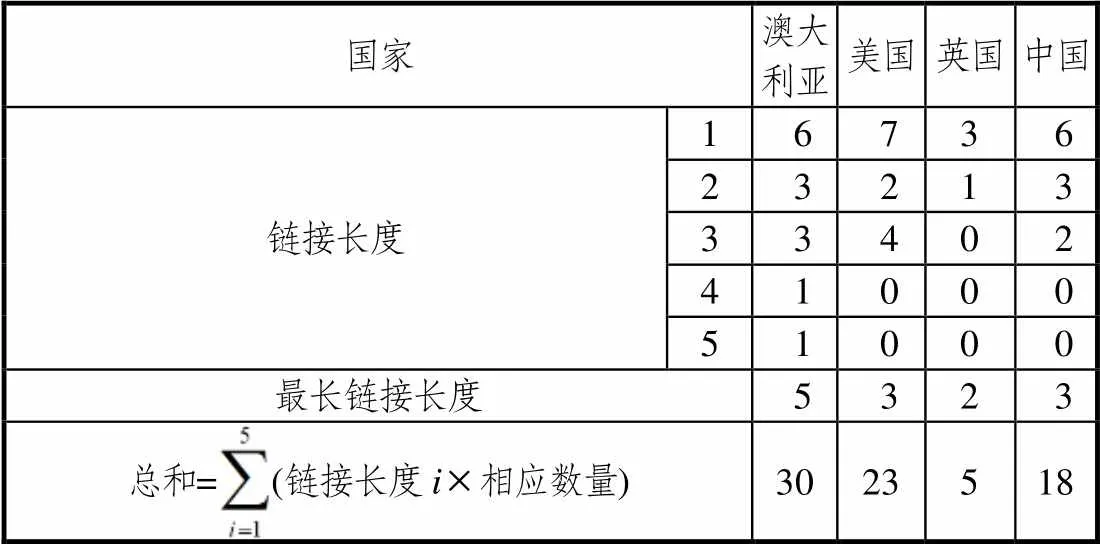
表2 4国“矩阵的概念”模块深度对比

观察表2，澳、美、英、中的最长连接长度分别是5、3、2、3，连接长度总和分别为30、23、5、18．由此可知，在“矩阵的概念”模块中，澳大利亚教材深度最大；虽然美国和中国最长连接的长度都是3，但美国的连接长度总和高于中国，所以，在“矩阵的概念”模块中，美国教材深度大于中国教材的深度；英国的最长连接长度和连接长度总和都是最小的，所以“矩阵的概念”深度也是最小的．

联系前面比较各国教材中矩阵内容广度的结果，可以发现澳大利亚教材的广度虽然最小，但其“矩阵的概念”模块的深度最大，说明澳大利亚教材在所有的矩阵知识中最注重矩阵基本概念的学习、理解和应用．比如，澳大利亚教材将逆矩阵与线性方程、两直线的位置关系、解的情况结合起来，而其他国家只是讲了逆矩阵与线性方程的关系，没有进行详细讲解．

（2）矩阵的运算．

4国“矩阵的运算”模块深度对比见表3．

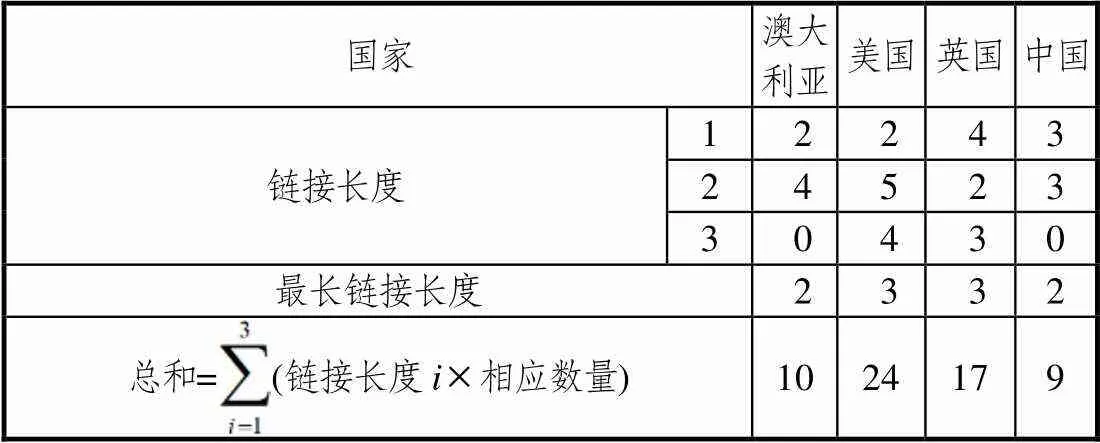
表3 4国“矩阵的运算”模块深度对比

由表3可知，澳、美、英、中4个国家最长连接长度分别是2、3、3、2，连接的长度总和分别是10、24、17、9，由此可以得出在“矩阵的运算”模块中，深度由高到低分别是美国、英国、澳大利亚和中国．

由比较结果可以看出，美国教材更注重矩阵运算的学习．英国教材在“矩阵的运算”模块中的一个特色，是将矩阵的乘法不满足交换律与复合变换的顺序不能颠倒结合起来；中国教材没有讲授用计算器进行计算，而且只局限在二阶矩阵和平面向量，所以深度较浅．

（3）图形的变换．

4国“图形的变换”模块深度对比见表4．

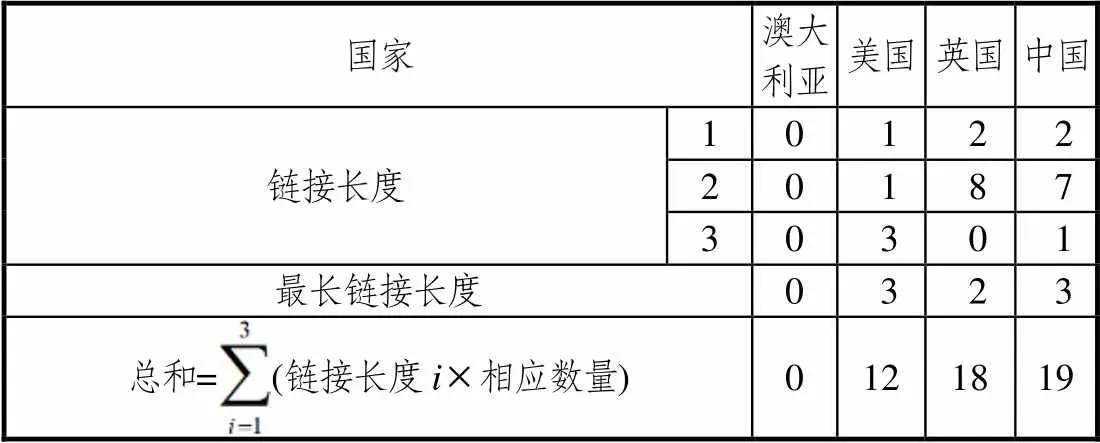
表4 4国“图形的变换”模块深度对比

由表4可以发现，澳大利亚教材没有涉及“图形的变换”模块的知识，其他3个国家最长连接的长度分别为3、2、3、连接长度的总和分别是12、18、19．由此可以知道，“图形的变换”模块中中国教材的深度最大，美国和英国的深度相差不大．

中国教材从图形变换的直观图象来认识矩阵及矩阵的意义，多次通过直观图形理解矩阵的意义，用矩阵表示图形的变换，因此，“图形的变换”模块深度比较大．其他两个国家的教材也各有特色，从不同角度将图形变换与矩阵知识结合起来：美国教材由等距变换讲授平移变换的知识，重点将矩阵、矩阵的运算和图形的变换结合起来；英国教材将复合变换的顺序和矩阵乘法不满足交换律进行比较．

（4）行列式及其它．

4国“行列式及其它”模块深度对比见表5．

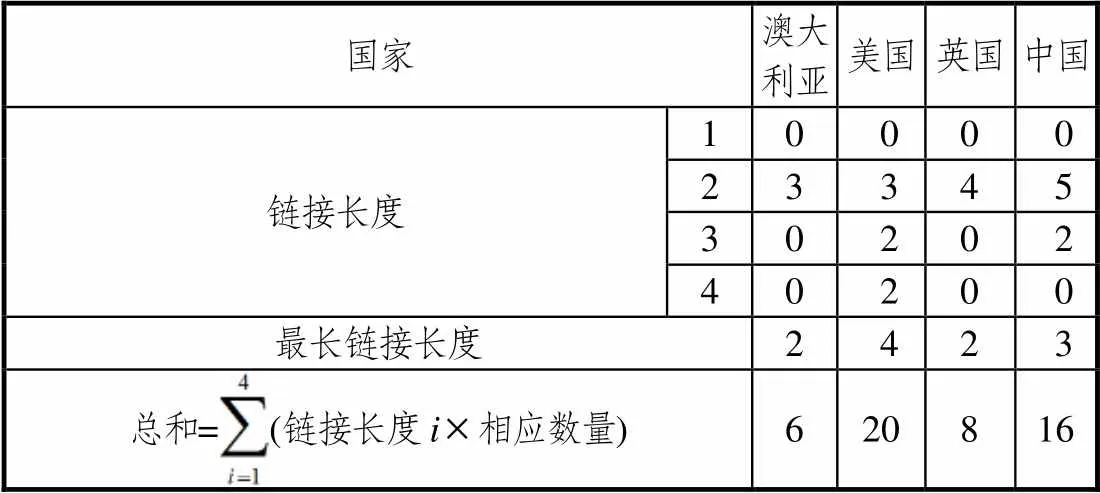
表5 4国“行列式及其它”模块深度对比

由表5可以发现，澳、美、英、中4个国家连接长度为2的连接数量最多，分别为3条、3条、4条和5条，最长连接的长度分别是2、4、2、3，连接长度总和分别为6、20、8、16．由此可以看出，“行列式及其它”模块中深度由高到低，分别为美国、中国、英国和澳大利亚．

在“行列式及其它”模块中，美国教材矩阵内容的深度最大，讲授了很多其他国家没有涉及的稍难的内容；中国教材深度次之但适宜，而英国和澳大利亚的教材略微简单．该模块是对矩阵知识的补充，教材应把握好知识的广度和深度，在初步学习矩阵知识时，不宜知识过多、难度过大．

如果将每个模块中4个国家的深度次序由高到低分别赋值4分、3分、2分和1分，可以得到4国教材矩阵内容深度的堆积柱状图，需要在此说明的是：以下对教材中矩阵内容深度的比较并非对各个国家教材进行排名，只是为了更直观地展示各国在深度方面的不同．

由图6的综合比较图可知，美国教材在4个模块中的深度比较均衡，都比较大；中国教材的矩阵内容整体深度也比较大，但低于美国，分布略有不均，“矩阵的运算”模块比其他3个国家深度小；英国教材矩阵内容的整体深度不算太大，“矩阵的概念”深度较小；澳大利亚教材矩阵内容的深度最小，而且教材中没有编排“图形的变换”．

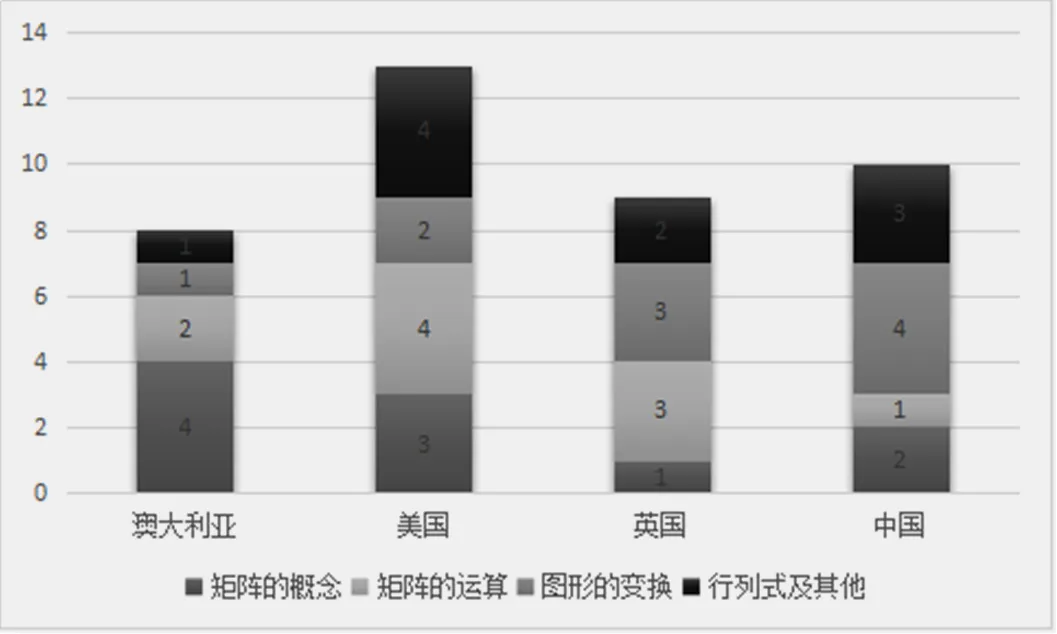
图6 4国教材中矩阵内容深度综合图

5 结论与建议

5.1 结论

在广度方面．美国教材涉及矩阵的概念是4个国家中最广泛的，中国教材中矩阵内容的知识广度也比较大，但与美国相差近16%，主要是因为中国教材对矩阵的运算和行列式部分讲解得比较少．与其他3个国家相比较，中国教材不要求让学生运用计算器进行矩阵有关的运算．在英国和澳大利亚的教材中，矩阵部分的知识点广度相比其他两个国家要小一些，澳大利亚教材中矩阵的知识广度最小．

在深度方面．在矩阵内容的不同模块中，每个国家教材的深度都存在一定的差异．在“矩阵的概念”模块中，深度由高到低的国家分别是：澳大利亚、美国、中国、英国；在“矩阵的运算”模块中，深度由高到低的国家分别是：美国、英国、澳大利亚、中国；在“图形的变换”模块中，深度由高到低的国家分别是：中国、英国、美国、澳大利亚；在“行列式及其它”模块中，深度由高到低的国家分别是：美国、中国、英国、澳大利亚．总体来看，美国教材中矩阵内容的深度最大，中国和英国次之，澳大利亚教材的深度最小．

5.2 建议

根据研究结论，对中国高中数学中矩阵内容的教材编写提出以下几点建议．

（1）保持优势，重视“双基”．相比较而言，中国教材更适宜学生学习，矩阵内容的广度和深度都处于较高水平，很多例题需要概念性的理解，但是略微忽视了学生矩阵运算技能的培养．在培养运算技能方面，只编写了二阶矩阵的加法、平面向量、二阶矩阵的乘法，对矩阵的认识存在一定的局限性，理论性较强．由于高中生第一次接触并学习矩阵内容，所以应加强矩阵基础知识、基本运算技能的训练．“双基”是中国数学教育的一个特色，在矩阵的教材编写中，也应保持传统教育的优势，保证学生既能较全面地认识矩阵这一数学工具，也能很好地完成矩阵的基本运算，为以后的学习打好基础．

（2）广度和深度相适宜．中国教材中矩阵内容的广度和深度都处于较高的水平，以矩阵发展的历史轨迹为思路编排，从图形的变换认识矩阵．在矩阵知识的广度和深度方面，很难确切地断定编排哪些知识点更好，可以以有助于学生认识、理解和应用矩阵为目的进行编排．矩阵内容对学生来说比较陌生，适当地增加数学知识的广度并保持一定的深度能够增强学生对矩阵的认识和理解．比如，可以介绍三阶矩阵的概念和三阶行列式的计算方法，这些能够培养和锻炼学生从特殊到一般的思维方式．

（3）合理运用信息技术．其他3个国家的教材都涉及了如何运用计算器进行矩阵的有关运算，中国教材中只有矩阵的笔算．计算器是一种学习的工具，有必要教会学生如何用计算器进行检验和探究与矩阵有关的问题，这也应该是高中生应掌握的一项基本技能．虽然中国教材中包含的矩阵相关计算比较简单，计算比较容易，但计算器作为一种运算工具，教师应该在适当的时候教会学生使用，为学生以后的学习做好准备．如在学生进入大学后遇到复杂的矩阵问题时也可以进行思考，不必因为笔算复杂而停止研究．

（4）完善高中矩阵内容的知识结构．4个国家高中数学教材中一共涉及69个与矩阵相关的概念，其中，中国有39个与矩阵相关的概念，可以适当增加一些有必要的概念、减少一些不适合高中生的概念，完善高中教材中矩阵内容的知识结构，以便更适合中国高中生的数学认知结构．一个更完善的矩阵知识结构有助于教师在备课、阅读数学教材时运用概念图来整体把握矩阵知识的框架和教学思路，提高知识结构化水平，从而更好地评价学生的知识掌握情况，促进学生形成更深刻广泛的知识迁移，以便更好地理解矩阵相关知识．

[1] 邵光华，章建跃．数学概念的分类、特征及其教学探讨[J]．课程·教材·教法，2009，29（7）：47–51．

[2] NOVAK J D, GOWIN D B. Learning how to learn [M]. New York: Cambridge University Press, 1984: 40–41.

[3] 王建波．中美澳初中数学统计课程难度的比较研究[J]．数学教育学报，2017，26（4）：50–55．

[4] 吴立宝．初中数学教材代数内容的国际比较研究[J]．数学教育学报，2016，25（4）：33–36．

[5] 李鹏．“中国”“美国”“巴西”数学教材“比和比例”内容的比较研究[J]．数学教育学报，2016，25（6）：46–50．

[6] 胡典顺，薛亚乔，王明巧．中国和美国小学数学教材中问题提出的比较研究[J]．数学教育学报，2016，25（4）：37–41．

[7] 王建波，曹一鸣．中美澳初中数学教材统计内容比较研究[J]．数学教育学报，2016，25（3）：14–19．

[8] 刘荣玄，朱少平．概念图引导型构图题的研究与实践[J]．数学教育学报，2017，26（2）：86–91．

[9] 于志．概念图评价的试题设计——美国概念图评价研究的新进展[J]．教育测量与评价，2009（11）：56–59．

[10] 赵国庆．概念图、思维导图教学应用若干重要问题的探讨[J]．电化教育研究，2012（5）：78–84．

[11]  CHENG C W, GREG C L, HUANG K L. Using concept maps to aid analysis of concept presentation on high school computer textbook [J]. Education and Information Technologies, 2004, 9 (2): 185–197.

[12] STOYANOVA N, KOMMERS P. Concept mapping as a medium of shared cognition in computer——Supported collaborative problem solving [J]. Journal of Interactive Learning Research, 2002, 8 (3): 309–323.

[13] 王嵘，章建跃，宋莉莉，等．高中数学核心概念教材编写的国际比较——以函数为例[J]．课程·教材·教法，2013，33（6）：51–56．

[14] 章建跃，宋莉莉，王嵘，等．美国高中数学核心概念图[J]．课程·教材·教法，2013，33（11）：115–121．

[15] 张豪锋，赵耀远，吴金鸽．多维概念图之应用效果研究——以七年级“信息技术”课为例[J]．电化教育研究，2012（11）：98–102．

[16] 梁荣荣，何秀玲，陈雪姣，等．一种面向课堂教学的概念图自动生成方法[J]．中国教育信息化，2017（4）：89–92．

[17] 解加平，辛涛．概念图在评估学生学习中的应用[J]．全球教育展望，2014，43（1）：40–49．

Matrix Content in Senior High School Mathematics Textbooks from Australia, the United States, the United Kingdom, and China: An Analysis Using a Concept Map

HU Dian-shun1, WANG Chun-jing2, WANG Jing3

(1. School of Mathematics and Statistics, Central China Normal University, Hubei Wuhan 430079, China;2. Shuangqiao Middle School in Tianjin, Tianjin 300350, China;3. Foreign Language School in Yichun City, Jiangxi Yichun, 336000, China)

A concept map, which is an effective tool to organize and represent knowledge, not only presents the main line of the vertical development of its core concepts but also shows the horizontal linkage among concepts. Using a concept map, we explore and compare the breadth and depth of the matrix content in representative senior high school mathematics textbooks from Australia, the United States, the United Kingdom, and China. We found that U.S. and Chinese textbooks have advantages over the U.K. and Australian textbooks with respect to breadth and depth. We propose the following suggestions for textbook development and revision in China related to matrix content: maintaining the Chinese textbooks’ advantages on the “two basics,” balancing breadth and depth of the content, using information technology whenever it is appropriate, and improving the knowledge sequencing of matrix content in senior high school.

concept map; matrix; mathematics textbooks in senior high school; comparative studies

G40–059.3

A

1004–9894（2020）03–0037–06

2019–12–20

教育部人文社会科学研究规划基金项目——中小学核心素养测评的模型建构与实证研究（19YJA880012）；中央高校基本科研业务费专项资金资助——基于学习分析技术的高中数学核心素养评价模型研究（CCNU19TS029）

胡典顺（1965—），男，湖北孝感人，教授，博士生导师，主要从事数学课程和教学论研究．

胡典顺，王春静，王静．基于概念图的中外高中数学教材比较研究——以澳大利亚、美国、英国和中国教材中矩阵内容为例[J]．数学教育学报，2020，29（3）：37–42．

[责任编校：周学智、陈汉君]