清末中学几何教科书中“勾股定理”的演变研究
张冬莉,代 钦
清末中学几何教科书中“勾股定理”的演变研究
张冬莉,代 钦
(内蒙古师范大学 科学技术史研究院,内蒙古 呼和浩特 010022)
1904年《奏定学堂章程》颁布实施以后,中国中学数学教科书的编写得到了前所未有的发展.清末时期翻译的中学数学教科书中勾股定理内容的设置,在证明方法上主要采用面积处理法和直接引入法,其内容的特点主要有3个方面:(1)证明思想方法“执果索因”与“由因导果”并重;(2)以欧几里得证法的作图为基础演变出多种几何图形;(3)注重介绍勾股定理的变式与拓展,即三角形分别为直角、钝角、锐角的3种不同情况时,在各边上做正方形其面积之间的关系.其发展历程对当今中学数学教科书的编写有以下启示:证明方法应多元化,体现证明的灵活性;重视知识的应用与拓展,加强启发性和探究性.
清末;中学数学教科书;勾股定理
1 时代背景
勾股定理的内容即直角三角形三边之间的度量关系,始终是几何教育中重要的内容之一,无论是在东方还是西方,数学和数学教育发展都扮演着重要的角色.在欧几里得《几何原本》公理系统建立之后,其中第47个命题给出了对勾股定理的证明.徐光启曾赞扬《几何原本》中逻辑推理的严谨性,试图用这样的思想解决中国古代数学的问题.在中国,从公元前一世纪的《周髀算经》开始,直到西方近代数学的传入之前,勾股定理在中国也是重要的内容.自明清之际,西学输入,国人继起研究整数勾股形的学者颇多,在清末,翻译的大量适用于普通教育的中学数学教科书中都有关于勾股定理的介绍.
清末时期,是一个新旧交替的过渡时代,即旧的已经被动摇但还没有被淘汰,新的已经开始但还没有形成.清末中学数学教科书亦如此,无论是其内容、形式还是思想等方面都呈现了这种特征.在1904年以前,没有一套完整的、能够供应小学和中学水平的、学生使用的数学教科书,所以不得不在西方引进教科书,清末颁布的《钦定中学堂章程》(1902年)和《奏定中学堂章程》(1904年)也十分关注教科书的引进.国人逐渐认识到教科书的重要性:“欲使一国之教育日有进步,在多设学校,欲使教育有成效之可睹,在办理学校者之热心,而办理学校者所挟之利器,即教科书是矣.故兴办教育欲收取普及之效,必借有用之教科书.”[1]之前使用的教科书已经不能满足新时代的要求,因此编纂一套适应当时中国国情的教科书迫在眉睫.自1904—1912年,关于几何教学要求简明扼要,基本延续了1904年《奏定中学堂章程》提出的要求:“其讲几何,须详于理论,使得应用于测量求积等法.”[2]由此可见,对于学习几何中定理的要求必须懂得其论理,培养学生的逻辑思维.
这时,商务印书馆聘请一些学识渊博的具有新思想的学者开始进行翻译和编写教科书的工作.在这种体认下,顾澄、黄际遇、黄元吉等依据癸卯学制,从1903年12月开始积极翻译和编撰教科书,使中学数学教科书迈入新的发展阶段.
第一本“最新教科书”于1904年2月开始出版.由于每种、每门、每册书上都有“最新教科书”5个字,所以称“最新教科书”.该教科书的编纂者都倡导新式教育,他们中的成员有的办过新式学校,有的翻译过大量的西学书籍,还有的具有留学背景.编纂者新政思想的贯彻,使得该套教科书成为最适合当时中国国情的成功之作.正如郑鹤声所指出:“商务印书馆编辑之最新教科书,实开我国学校用书之最新记录.”[1]这些翻译数学教科书者,他们并不一定限制在数学教育领域.不仅有顾澄、黄际遇、崔朝庆等数学家,还有一些非数学家的人员也参与到数学教科书建设中来,做出了重要贡献.如谢洪赉、丁福保不是数学家,但也编译编写数学教科书.这可能是当时他们认识到数学在整个教育中的重要性.
2 教科书案例
在清末初建学堂之时,数学教育制度的制定及数学教科书的编写等均为十分紧迫的问题,在中国一筹莫展之际,通过各种途径借鉴和学习了日本和西方数学教育的经验和教训,并且积极翻译西方数学教科书,努力缩小中国数学教育与日本、西方数学教育水平的差距.由表1可知,这一时期以翻译日本和西方教科书为主,这些教科书的翻译在清末民初是刻不容缓的.勾股定理内容设置的几何教科书有多种,呈现出多元化趋势.教科书之间虽然有些差别,但是教科书中勾股定理内容的编写理念、内容设置及相关的特点之间差异甚小.
2.1 编写理念及编排形式
清末是中国传统文化和西方现代文化碰撞和交融的大变革时期,也是中国传统数学教育走向近代化的转型时期[3].因此这一时期数学教育的特点和以往的数学教育有显著差异.清末国人的数学教育思想、制度等方面的特点具体也反映在教科书的建设上,可以概括为数学教科书宏观特点和教科书编写的微观特点.

表1 清末中学几何教科书概况(部分)
清末数学教科书中勾股定理内容主要以定理的描述、定理的证明方法以及变式或拓展、习题等顺序进行编排.但是教科书中的编排形式各不相同.清末谢洪赉、周达等学者翻译的《最新中学教科书几何》就是典型例子,采用中国传统的文章从右至左的竖排形式编写.而且他把原著中的印度阿拉伯数字和加减符号以外的数学符号,全部用中国传统数学符号甲乙丙丁代替,页码均用中国大写数字表示,几何图形的顶点、端点等不用A、B、C等字母而用汉字(如图1).

图1 最新中学教科书
又如长泽龟之助著,崔朝庆译的《中等平面几何学阶梯》,译者是文字介绍部分采用竖排形式,而数学表达式部分采用竖排和横排的混合编排形式,同时采用西方数学符号.清末出版的数学教科书也有横排编写的,而采用的数学符号仍然是中国传统的数学符号.如杨清贵翻译日本原滨吉著的《最新平面几何教科书》(1905)就是其中一个代表(如图2).

图2 《中等平面几何学阶梯》与《最新平面几何教科书》
清末有些数学教科书也有完全采用西方数学教科书的编排形式及数学符号.特别是在日本出版的数学教科书,如长泽龟之助著,周达翻译的《新几何学教科书(平面)》.日本数学家菊池大麓著,仇毅翻译的《中学校数学教科书几何之部》(如图3).除此之外,黄元吉等学者也强调按西方数学教科书形式编写的重要性,在此不再一一赘述.

图3 《新几何学教科书平面》与《中学校数学教科书 几何之部》
总之,教科书中问题皆以图,证明并用记号,置轨迹于作图题之内,使学者知其应用.书中的标题都黑体加粗,以省目力.排版有秩,适合阅读.在教科书的最后有商务印书馆出版的其它书目的广告等.
在此引用《新几何学教科书平面》“例言”说明其编辑理念:
本书为中等教育程度合于中学校师范学校教科之用其编制之大旨为揭之如次:
1. 别学科之联络.2. 著重应用.3. 论理学之术语不侵占正文.4. 用器画之联络.5. 比例理之简明.6. 注释历史.7. 定理之一览表.8. 问题之选择问题最为精审.9. 补习问题.10. 代数学与几何学解法之比较.11. 重用记号.12. 纸幅酌留空白.
在例言中,编译者明确提到该书的使用范围.即该书适用于中学教授,该套教科书力求别学科之联络,虽专论几何,但时而以算数代数两科印证,互较之必有路路皆通,头头是道之乐;重视应用;增其趣味;几何学与用器画有密切的关系,这也是该书独特所在,比如作图时,已知线用细线表示,所添加的辅助线用断续线来表示,所求的用粗线表示,这样,就可以知道作图的先后顺序,通过用器画一举两得;重视历史,对读者不仅有益且增长趣味,其历史内容则是参考英国希腊算学史以及法国人编写的几何学等;书中重用记号,与其口讲不如指画,与其文字解说不如以记号证明,简洁而清晰;每节的后面或者一小节结束的地方,都留一些空白的地方,学生可将读书的感悟或题目的解答过程写在纸尾,防止遗忘.该书之卷末附载定理一览表以便引用时检查.
2.2 清末中学数学教科书中勾股定理内容设置的形式及其特点
基于1902—1912年,清末中学数学教科书以翻译日本为主,欧美次之,国人自编处于起步阶段,故所选研究对象分为两类,即译自日本和译自欧美教科书.选取当时中学校使用较多的具有代表性的几何教科书进行详细研究,具体如表1所示.根据几何教科书中勾股定理内容的呈现方式,总结出定理证明的特点.
2.2.1 勾股定理内容设置的形式
(1)等面积处理法.
采用面积处理方法的核心就是使用演绎证明的分析法,即从命题的结论开始分析,一直追溯到已知的真命题.这种方法具有两大特征,一是构图方式,二是对图形进行必要的分割,将斜边上正方形分成两个矩形,通过证明四边形面积等于和其等底等高的三角形的面积的二倍.得到它们分别与两个直角边上正方形的面积相等,从而获得定理证明.这种把斜边上正方形分成两个矩形的思想对后人也有较大的影响.
例1[4],如图4,为直角三角形,为其斜边.则上之正方形等于上之正方形与上之正方形之和.即正方形=+.
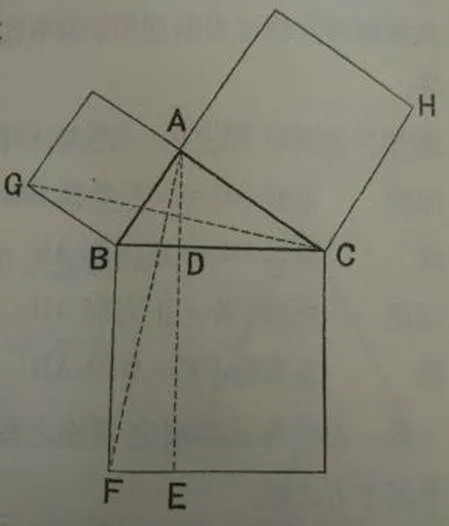
图4 例1
证明 自直角之顶点引垂线于斜边.而延长之与正方形之一边交于点.此引、.则两三角形、,边=(正方形之边),边=(正方形之边),角=角∠(角+直角),故此两三角形全相等,从而三角形=.然矩形与三角形共有底边.而高亦相等.故矩形=2三角形,同理,矩形=2三角形.故矩形=正方形,同理,矩形=正方形.故,正方形=.
系 表直角三角形之斜边之数等于表它二边之数之平方和.
例如表直角三角形之斜边之数为,表它二边、之数各为、,则2+2=2.何则,2为表上正方形之面积之数.2、2为表、上正方形之面积之数.故也.
该例题是欧几里得证法的原型.对于作图题目,将轨迹(辅助线)于作图题之内,是教科书中的特色之一.辅助线的做法可以归纳为两种方法:一是过一点作某条已知直线的垂线,另一种是过一点作某条已知直线的平行线.例1就是采用第一种作辅助线的方法,自直角之顶点引垂线于斜边.而延长之与正方形之一边交于点.对于第二种作辅助线的方法,如例2.
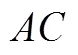
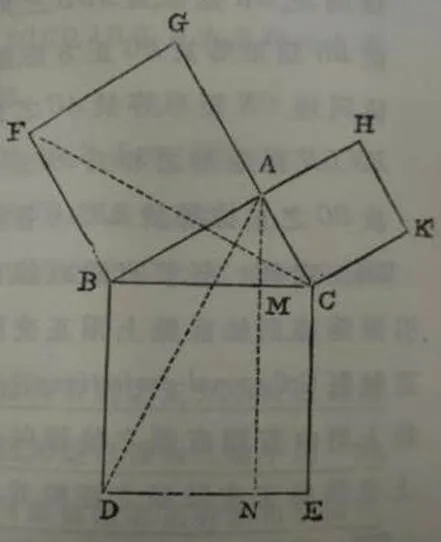
图5 例2
对于面积的处理方法,教科书中有给出以三角形的一条边向内作正方形的证法.
例3[5],如图6,于甲乙丙三角形中.命甲为直角.乙丙戊丁,甲乙庚己,甲丙辛壬为各边上之正方形.次将甲丁,庚丙连结.则甲乙等于乙庚.乙丁等于乙丙.甲乙丁角等于丙乙庚角.故甲乙丁,丙乙庚两三角形全相等.次使癸甲予平行于乙丁,则乙癸矩形等于甲乙丁三角形之二倍.又乙己正方形等于丙乙庚三角形之二倍.故乙癸矩形等于乙己正方形.
图6 例3
依同理丙癸矩形等于甲丙戊三角形之二倍.即等于乙丙辛三角形之二倍.亦即等于丙壬正方形.而乙戊正方形为乙癸,丙癸二矩形之和.故等于乙己,丙壬二正方形之和也.【注:此定理最为紧要.】
也就是说以构造三角形作为传递的中介,以直角三角形的各边向里作正方形,只要使得三角形也满足“同时和两个图形共底等高”即可.该证明的图形,在E. S. Loomis撰写的一书中第157个证明也有提到,是由一个美国人Richard Bell提供的证明方法[6].他是将两个图形分解成对应全等的子图块,并为每组对应的图块进行相同的编号,从而得到两个图形面积相等的结论(如图7).
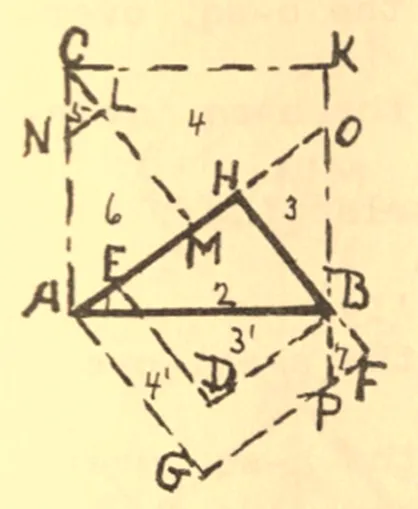
图7 Richard Bell证明方法
另外一种面积的处理方法就是构造出一个五边形,做一次面积减法,证明勾股定理,如例4.
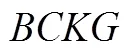
图8 例4
该图与中国古代赵爽证明勾股定理时所用思想理念是一致的,但是证明过程完全不同.赵爽在为《周髀算经》作注时,采用图形变换的方式证明勾股定理,其也属于面积法的一种.主要通过构造两个或多个全等直角三角形,把其中两个全等三角形进行旋转,将它们摆放在合适的位置,然后连接其中的一些顶点,得到一个新的图形.使得新图形的面积与原来图形的面积相等.
(2)直接引入法.
所谓直接引入法就是在教科书设置中,并不是通过验证的方法得到直角三角形斜边上之正方形等于直角旁二边上两正方形之和.而是直接给出定理的描述或者是表示形式,然后试证之.
然为一道线且与平行.
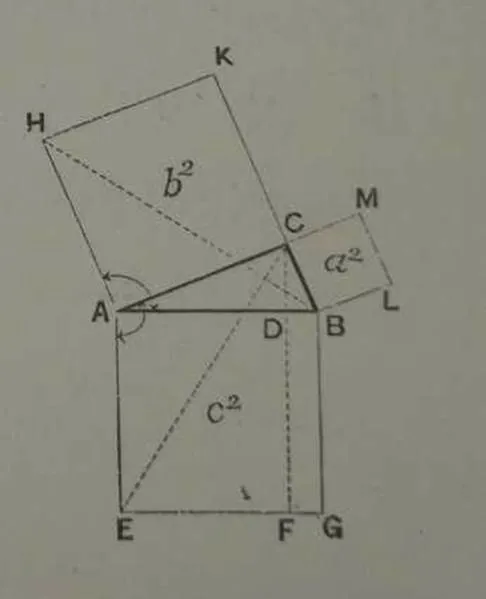
图9 例5证明
(此为辟塔果拉司氏【Pythagoras西历纪元年前约580年生约501年死】之定理也,此定理在辟塔果拉司氏以前已为世人所知,特自辟氏始证明耳.此定理为几何学中最要之理别示数个图解如图10所示,I图为直角二等边三角形乃特别之形也于铺方砖之地上可以实验古时因见此图而触悟乃使发明本定理者也.II图指明自大正方形内减去1、2、3、4四个相等直角三角形则所余者为斜边上之正方形又此4个直角三角形等于、,两矩形去之则所余者又为夹直角两边上正方形也.III图指明,
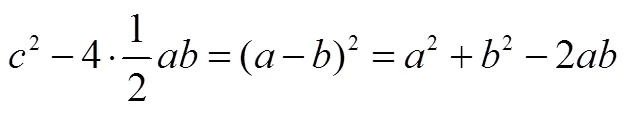
图10 图解
(3)推论(系).
同样在直角三角形内,根据直角三角形三边的关系,在利用面积的转换,从而得到新的结论.
系1[4]直三角形之一直角边上之正方形,等于斜边上之正方形与他边上之正方形之差.
证明 于甲乙丙三角形中.命甲为直角.则“乙丙2=甲乙2+甲丙2”.故“甲乙2=乙丙2–甲丙2”.及“甲丙2=乙丙2–甲乙2”.
系2[5]自直三角形之直角点.向斜边引垂线,则斜边依此垂线分为二部分.其一部分与斜边之积等于此一部分之邻边上之正方形.
系3[8]从直角三角形之顶点向斜边引垂线,此垂线上之正方形等于底边之二部分所包矩形.
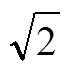
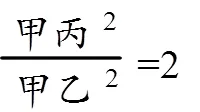
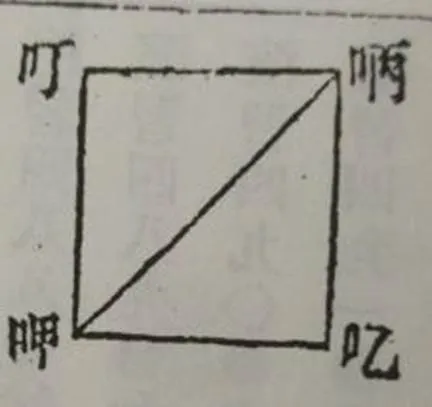
图11 推论
(4)三角形之间的关系(变式与拓展)[10].
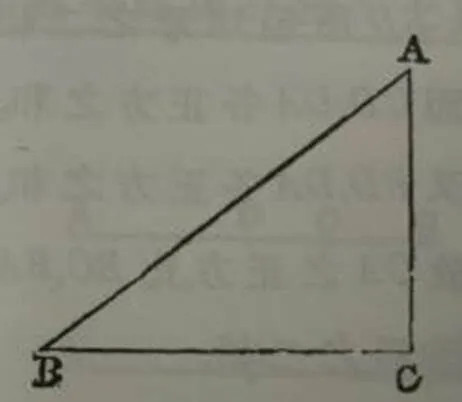
图12 变式与拓展(一)
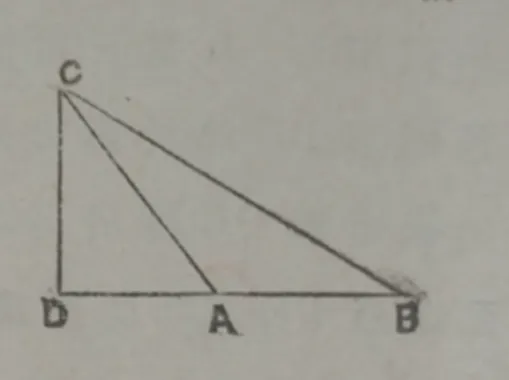
图13 变式与拓展(二)
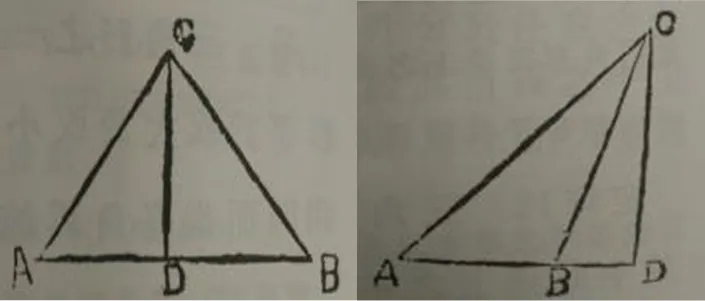
图14 变式与拓展(三)
此等式之两边各加2,
自以上定理(i)(ii)(iii),可知三角形一边上之正方形,视其对角为直角或钝角或锐角,因而等于或大于或小于他二边上正方形之和.
该定理的逆定理也是合理的,因而得下之系.
系 三角形之一角视其对边上之正方形等于或大于或小于它二边上正方形之和,因而为直角或钝角或锐角也.
对于三角形之间的关系,还有如下定理(三角形中线定理).
定理 三角形二边上正方形之和等于半底边上之正方形与自顶点至底边中点所作直线上正方形之和之二倍.
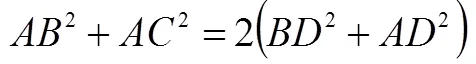
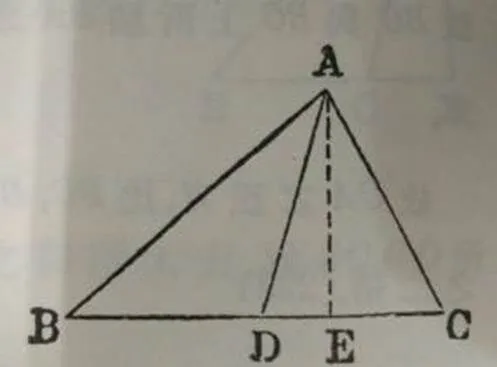
图15 定理证明
2.2.2 勾股定理证明内容的特点分析
(1)证明思想方法“执果索因”与“由因导果”并重.
如果从题设的已知条件出发,运用一系列有关已确定的命题作为推理的依据,逐步推演而得到要证明的结论,这种证明方法为综合法;反之,如果推理方向中由题断到题设,论证中步步寻求使其成立的充分的条件或已经成立的事实,这种证明方法为分析法[10].欧几里得证法采用的就是分析法,执果索因,用三角形共底等高面积相等的方法证明,从而得出结论.在清末几何学教科书中,综合法和分析法均有体现.由此可见,在翻译教科书的过程中,展现了不同文化差异下的不同思维方式,皆是各自文明中思想传统的直接体现.但值得一提的是,虽然清末时期有诸多新颖的数学知识自西方陆续传入,但是也应该与本土原有的知识相结合.可是在翻译几何教科书中,基本上没有介绍中国证明勾股定理的方法,忽略了中国原有的赵爽、刘徽的证明方法.中国自己的东西,很重要的部分反而被忽略,当时翻译教科书的译者也都是读过《周髀算经》《九章算术》等,但是当时外国人简介都进入到教科书中,但却没有对中国人的介绍.这些原本被重视的,反而被忽略.
(2)以欧几里得证法作图为基础演变出多种几何图形.
清末时期的中学数学教科书中,对于勾股定理的证明主要选取作图法.通常是以欧几里得证法的作图为基础,以某条边向里或者向外做正方形等演变出多种几何图形,用等积变换法证明定理.其次在图中添加辅助线也是教科书的特点之一,大部分的辅助线作法可以归纳为3种情况:① 过一点作某条已知直线的垂线;② 过一点作某条已知直线的平行线;③ 以三角形的一条边向外或者向内作正方形.但是在清末的几何教科书中,对于拼图法并没有介绍,只有1906年本的《新几何学教科书·平面》一本在脚注中,言简意赅地说明古时发现定理的实验法,同时又给出了两幅插图,用割截移补之法亦可证明该定理,并指出其它类此之图尚多.
(3)注重介绍勾股定理的变式与拓展.
由勾股定理变式得到,在一般的三角形一边上作正方形,视其对角为钝角或锐角时,即大于或小于它二边上正方形之和.在每一本教科书中都有对这部分内容的介绍.与清末时期中学数学教科书相比,中国现行中学数学教科书中不再介绍勾股定理的变式与扩展,只有设置勾股定理的逆定理相关内容,并用反证法予以证明.从这方面来讲,清末时期所学的数学内容要比现在难度大.
3 启示
20世纪初,欧洲掀起数学教育改革运动,在中学数学教育中英国数学家培利和德国数学家F·克莱因等人主张实施应用性、实验性内容和函数思想.于是几何内容被削弱,从那时起几何证明内容在中学几何教科书中逐渐减少.勾股定理的相关内容亦如此.但是由于历史发展滞后的原因,中国没有能够融入到数学教育改革潮流,翻译引进的中学几何教科书均为欧美19世纪中叶后的教科书,即为他们传统几何教学内容,中国没有与西方新的数学教育接轨.因此,清末数学教学内容基本为所谓的“陈旧的数学教学内容”中学几何教科书中的勾股定理的证明、拓展和应用等都体现了这方面的特征,勾股定理的这些内容很好地实现了其历史使命.
诚然,清末数学教科书中勾股定理的内容设置理念和方法对当前的中学数学教学仍然具有重要的借鉴作用.在数学教育改革中不能随意地采取“二元论”的极端做法,亦不能无端地用过时论的态度去面对过去的历史,而是用理性的态度对待历史,从过去数学教育蕴含的内容中选其精华,合理地运用到当前的数学教育中是当务之急.在中国的一般做法是,新教科书开始使用后旧教科书立即销声匿迹.而在美国等发达国家并不是这样,如,在美国过去50年、100年、150年的中小学数学教科书经常被重印出版,美国的广大中小学数学教师可以参考这些过去的教科书进行自己的教学.这是中国学者应该借鉴的积极方面.
纵观清末时期1902—1912年间的中学几何教科书中勾股定理内容设置之变迁历程,数学教育者们在新与旧、中与西的巨大鸿沟之间搭设起桥梁,将西方数学相关知识引进到中国.清末在几何教科书中设置的勾股定理命名为毕达哥拉斯定理.在翻译的中学几何教科书中体现了教科书编译者对西方数学文化完全接受的态度,各种教科书极为重视几何证明的方法.在清末,关于勾股定理内容设置的部分,主要呈现方式按照定理的证明—推论—变式—拓展4个方面进行编排,大多数几何教科书设置了定理的逆定理、推论、扩展和应用,结构完整,表述严谨.故在勾股定理章节编排设置上得到以下启示.
3.1 证明方法应多元化 体现证明的灵活性
对于证明的选取,建议教科书在编写上要多介绍勾股定理的几个著名的证法及其有关的一些著名问题,使学生感受证明的灵活性,感受勾股定理的丰富文化内涵.清末教科书中定理证明的选择和表述,多数采用欧几里得分析法的证法,从命题结论开始构造正方形,执果索因.该方法是纯粹几何图形之间的关系,不直接涉及数量,证明极其严格,论述十分严谨,欧几里得的证明方法的学习,对培养学生严谨的逻辑思维能力具有重要的促进作用.但是对数学基础一般的学生而言,学习和掌握欧几里得的证明方法及其数学思想是难以达到的.虽然至今为止,证明方法已有五百多种,实际上,有很多的作图方法都是由欧几里得的作图法得到启示.
3.2 重视知识的应用与拓展 加强启发性和探究性
勾股定理的逆定理是应用广泛的定理之一.至今在建筑上,还用该方法“放线”,做直角三角形.几何教科书中逆定理的设置,对培养学生逆向思维有重要意义.数学教育的目的之一是培养学生知识的拓展性和思维的开扩性品质.从这个意义上说,清末几何教科书中的勾股定理拓展性内容的设置,渗透“以形证数,数形结合”的思想方法,蕴含着深刻意义.故在教科书编排中应加入更多的扩展内容,以探究形式学习数学知识的设计,更加突出学习数学的过程,加强了启发性和探究性.
回顾清末时期翻译几何教科书的发展史,在“无选择,唯以多为贵”的形势下,满足教师学生的需求是新学制教科书发展的基本起点.无论是在什么时期,教科书的编排都应着力于内容体系合理、严谨.总之,清末中学几何教科书的建设与当时的社会背景、文化传统、政治制度等有着千丝万缕的关系.其发展的最大特征是以翻译编译为主,直接翻译外国教科书或直接使用外文教科书,然后逐渐转变为编译数学教科书使其尽量符合中国的国情,最终实现自编教科书的历史进程.毋庸置疑,过去的东西并不是过时的.一百多年前的教科书发展历程,对当今课程改革也有借鉴作用.勾股定理不能只作为一个单纯的定理进行学习,它的逆定理、推论和拓展等应用十分广泛.目前,中国中学在编排勾股定理章节时,也只介绍勾股定理及其逆定理,相比较而言,均不如清末数学教科书内容丰富.
[1] 郑鹤声.三十年来中央政府对于编审教科图书之检讨[J].教育杂志,1935,25(7):23.
[2] 课程教材研究所.20世纪中国中小学课程标准·教学大纲汇编(数学卷)[M].北京:人民教育出版社,2001:205-206.
[3] 李春兰.中西数学文化碰撞下的清末中学数学教科书[J].内蒙古师范大学学报(教育科学版),2013,26(4):92-93.
[4] 生驹万治.几何学教科书[M].东京:东亚公司,1908:137-138.
[5] 黄元吉.中学教科书平面几何[M].3版.北京:商务印书馆,1913:111-112.
[6] LOOMIS E S. Pythagorean proposition [M]. 4th ed. ERIC, 1972: 189.
[7] 长泽龟之助.中等平面几何学阶梯[M].崔朝庆,译.上海:会文学社,1906:89-90.
[8] 长泽龟之助.新几何学教科书·平面[M].周达,译.东京:东亚公司,1906:106-108.
[9] 林鹤一.几何教科书[M].上海:普及书局,1906:116-117.
[10] 谢洪赉.几何学平面部[M].北京:商务印书馆,1906:23.
A Study of the Evolution of the Pythagorean Theorem in the Geometry Textbooks for Secondary Schools in the Late Qing Dynasty
ZHANG Dong-li, DAI Qin
(Institute for the History of Science and Technology, Inner Mongolia Normal University, Inner Mongolia Hohhot 010022, China)
After the Guimao Educational System was implemented in 1904, the compilation of Chinese secondary school mathematics textbooks developed at unprecedented levels. Mathematics textbooks for secondary school in the late Qing Dynasty contained two proof methods for the Pythagorean Theorem: an area treatment and a direct proof. There are three main characteristics of the Pythagorean Theorem proofs in these textbooks: (1) Paying equal attention to the method of proof that begins with the givens and works toward the desired conclusion and the method of proof that begins with the conclusion and works backward toward the givens; (2) various geometric figures were used to base proofs; (3) introducing variations and extensions of the Pythagorean Theorem, that is, considering the relationship between the squares and their areas in the three different cases of right triangles, obtuse triangles, and acute triangles. With respect to the compilation of mathematics textbooks in middle school, this development process suggests that the method of proof should be diversified in order to reflect the flexibility of proof, that attention should be paid to the application and extension of knowledge, and that students’ enlightenment and inquiry should be fostered.
late Qing dynasty; mathematics textbook; secondary school; Pythagorean Theorem
G423.3
A
1004–9894(2020)03–0079–07
2020–03–06
2020年度内蒙古自治区高等学校科学研究项目——民国时期数理逻辑教科书研究(1920—1949)(NJSY20307)
张冬莉(1992—),女,内蒙古呼伦贝尔人,博士生,主要从事数学教育与数学史研究.代钦为本文
.
张冬莉,代钦.清末中学几何教科书中“勾股定理”的演变研究[J].数学教育学报,2020,29(3):79-85.
[责任编校:周学智、陈汉君]

