基于一道典型例题剖析求解级数问题的方法

王成强

(成都师范学院 数学学院,四川 成都 611130)

数项级数理论是《高等数学》《数学分析》课程中重要的组成部分,是这两类课程的教学重点。数项级数理论是数列极限理论的延伸,是函数项级数理论,如幂级数理论、Fourier级数理论的基础,又与无穷限反常积分之间有紧密的联系[1,2]。另一方面,数项级数涉及(可数)无穷多数求和,其学习需要一定的抽象思维能力、转化划归能力与科学计算能力。因此,数项级数理论也是《高等数学》《数学分析》这两类课程的教学难点。经过几年的教学实践与反思,笔者认为,克服数项级数理论教学上的困难以确保“保质保量”地完成该部分知识点的教学的有效策略有:挑选典型例题,精讲细讲典型例题,注重变式教学与一题多解,恰当合理“配置”课后习题。出于精讲细讲典型例题的想法,本文研究一道教材例题的一题多解。

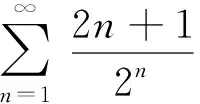
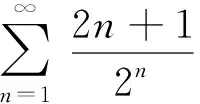
综上,问题(*)是一道典型的数项级数问题,具有很高的研究价值。数项级数有关的最重要的问题有二,其一为判断级数是否(绝对)收敛,其二为求收敛级数的和。本文拟给出问题(*)的多种解法,以期在大学数学数项级数理论的教学领域引发更多思考。

1 问题(*)的多种解法

1.1 证明级数收敛的七种方法

收敛。

注4方法6将数项级数理论与幂级数理论“联结”在一起,不仅带来了解题的方便,也使得所学的数学知识更加体系化。

1.2 求正项级数和的七种方法

方法乙利用“错位相减”的想法,有

方法丙同样,利用“错位相减”的想法,有

注7方法乙、丙的方法,常称为错位相减法,已经渗透到中学数学,它是求级数∑un/vn({un}是等差数列,{vn}是公比不为0,1的等比数列)和或者部分和数列经典方法。从方法乙、丙的过程可看出,直接对(无穷)级数运用错位相减法,比对其部分和数列要更简洁些。

方法丁利用Abel分部求和公式化简部分和数列,有

方法戊利用Abel分部求和公式的想法,有

εnαn-ε0α0,

注9方法己、庚的想法都是引入辅助幂级数用来计算数项级数的和函数。相较于数项级数,函数项级数的和函数的计算方法更加丰富,例如,幂级数的和函数的求法有求导法、求积分法以及解微分方程法。

2 结束语

经探究,本文基于不同视角对问题(*)(一道典型的数项级数大学数学教材例题)发展出了多种求解策略:分别基于d’Alembert比式判别法、Cauchy-Hadamard根式判别法、比较判别法、Abel判别法、Dirichlet判别法、幂级数法、积分判别法等观点提出了七种方法以证明问题(*)涉及的正项级数收敛;分别基于“列项+两项相消”、“错位相减”、Abel分部求和法、幂级数法等观点提出了七种方法以计算出问题(*)涉及的正项级数的和。笔者认为,本文的研究能为级数理论中很多“抽象”的结论提供应用的示范案例。