基于免疫疗法的肿瘤免疫系统的Filippov 模型的研究

王令君 杨友苹

(山东师范大学数学与统计学院，250358，济南)

1 引 言

自20世纪90年代起,细胞免疫治疗受到科学界关注,21世纪免疫治疗在肿瘤治疗领域中取得了诸多进展.研究表明免疫系统可以识别并消除肿瘤细胞,因此如何利用免疫治疗增强免疫系统的抗肿瘤活性,控制和清除肿瘤细胞意义重大.一些研究者用偏微分方程的空间模型和常微方程的非空间模型来研究肿瘤免疫系统的相互作用[1,2],但并未研究肿瘤免疫反应中免疫治疗的作用.目前有人提出了在肿瘤微环境下,通过免疫治疗[3-6],如接种疫苗来刺激免疫系统或直接注射T细胞或细胞因子来增加免疫系统活性,从而达到治疗的目的.有研究提出肿瘤细胞与免疫系统的相互作用可看作捕食与被捕食模型,其中肿瘤细胞是被捕食者,免疫细胞是捕食者的具有常数治疗效果的动力学模型[7,8].目前的肿瘤免疫治疗策略主要集中在四个方面:一是肿瘤疫苗, 如DC疫苗,DNA疫苗等；二是细胞因子,如IL-2,IL-7等；三是免疫检查点抑制剂,包括CTLA-4抗体, PD-1抗体,PD-L1抗体等；四是过继细胞输入(ACT).但这些治疗措施若持续实施不仅其疗效会降低还会对宿主免疫系统带来一定程度的伤害,因此需要更合理的肿瘤—免疫治疗策略,来控制和清除清除肿瘤细胞.本文采取的具有Logistic[9]增长和HollingⅡ增长[10]的具有阈值策略的捕食与被捕食模型在免疫治疗中更具有现实意义.本文以肿瘤细胞为控制目标,当肿瘤细胞数量达到一定的阈值时,采取免疫治疗,通过直接注射免疫细胞的方式,增加免疫系统抗肿瘤活性的同时降低肿瘤细胞的增长,否则不采取免疫治疗.本文研究了关于肿瘤免疫效应系统的Filippov模型的全局动力学行为,用Matlab对结论进行了数值模拟分析了阈值策略的免疫疗法的效用.

2 Filippov 模型

建立如下的模型：

(1)

(2)

令z=(x,y)T,σ(z)=x-xc,

则系统(1)和(2)可转化为如下模型

(3)

定义1(i)∑∈M是滑动段,当且仅当在∑上有〈n,f1(z)〉>0且〈n,f2(z)〉<0;(ii) ∑1∈M是逃逸区,当且仅当在∑1上有〈n,f1(z)〉〈n,f2(z)〉>0,其中n=(1,0)T表示σ(z)在M上的梯度.

定义2(i) 如果f1(z)=0,σ(z)<0,或者f2(z)=0,σ(z)>0,则称z是系统(3)的真平衡点;

(ii) 如果f1(z)=0,σ(z)>0,或者f2(z)=0,σ(z)<0,则称z是系统(3)的假平衡点;

(iii) 如果αf1(z)+(1-α)f2(z)=0,σ(z)=0,其中

则称z是系统(3)的伪平衡点.

注1设定义在区域G1上的系统为S1,定义在区域G2上的系统为S2.由定义2 可知,当轨线穿过不连续边界M时,其系统动力学就会改变,所以一个假平衡点不会稳定.

3 全系统的动力学性态

3.1子系统S1的动力学性态子系统S1的形式为

(4)

引理1系统(4)在G1无极限环.

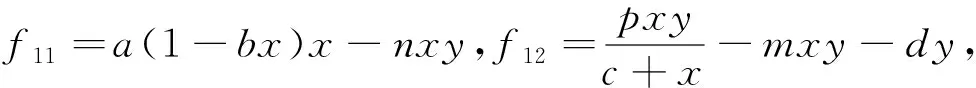
证(i)系统(4)在G1上的雅克比矩阵为

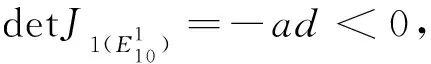
下面只讨论R01>1时,系统(4)的正平衡点.有下式成立

(5)

方程组(5)的第二式等价于

g1(x)=mx2+(d+mc-p)x+dc=0.

(6)

定理2如果R01>1,p-d-mc>0,则Δ1>0,E12在G1是全局渐近稳定的.

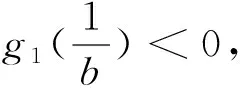
3.2子系统S2的动力学性态子系统S2的形式为

(7)

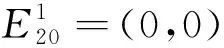
引理2系统(7)在G2无极限环.

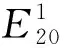
R02>1时,子系统S2有下式成立

(8)

方程组(8)的第二式等价于

g2(x)=mx2+(d+mc-p-s)x+(d-s)c=0.

(9)

同理于子系统S1的正平衡点的讨论,对子系统S2有以下结论.

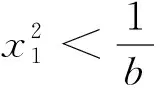
Δ2=(p-d-mc+s)2-4m(d-s)c.

定理4如果R02>1,p-d-mc+s>0,则Δ2>0,E22在G2是全局渐近稳定的.

4 全局动力学及数值模拟

因为R02>R01,Δ2>Δ1,所以只需讨论R01>1时,系统(3)的动力学行为.

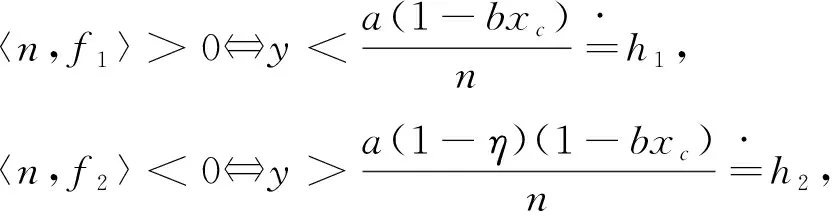
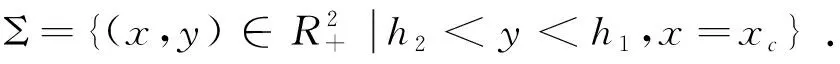
由Filippov 凸方法[11],得滑动模型为

(10)

令F(y)=0,得

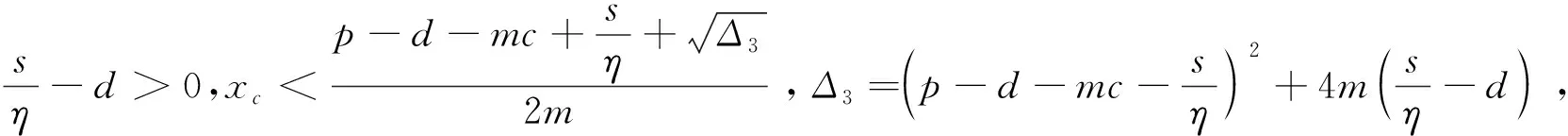
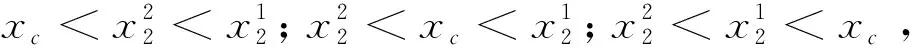
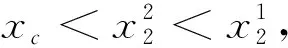
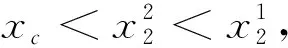
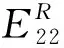
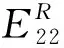
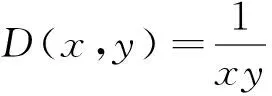
同理在D2,有

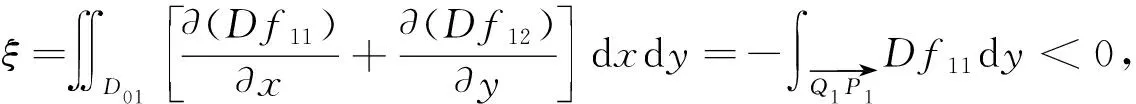
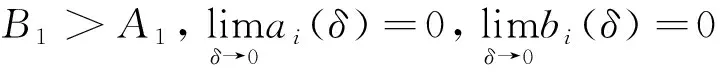
=aη(1-bxc)(lnB1-lnA1)>0,

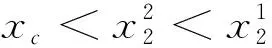
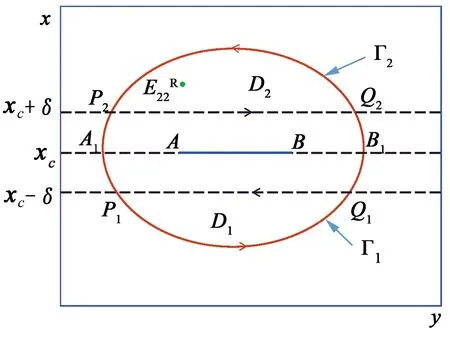
图1 系统(3)极限环不存在的情况

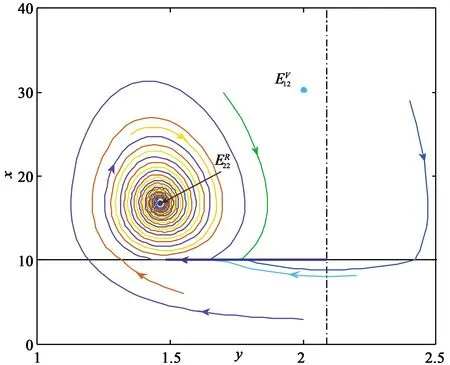
图全局渐进稳定

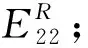
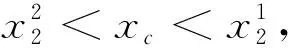
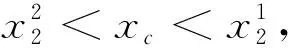
此时无论轨线是从G1出发还是从G2出发,都将切中滑动段趋于伪平衡点Es,且肿瘤细胞数量等于所给阈值水平.定理6的数值模拟图见图3.

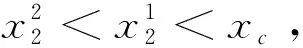
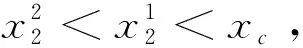
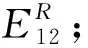
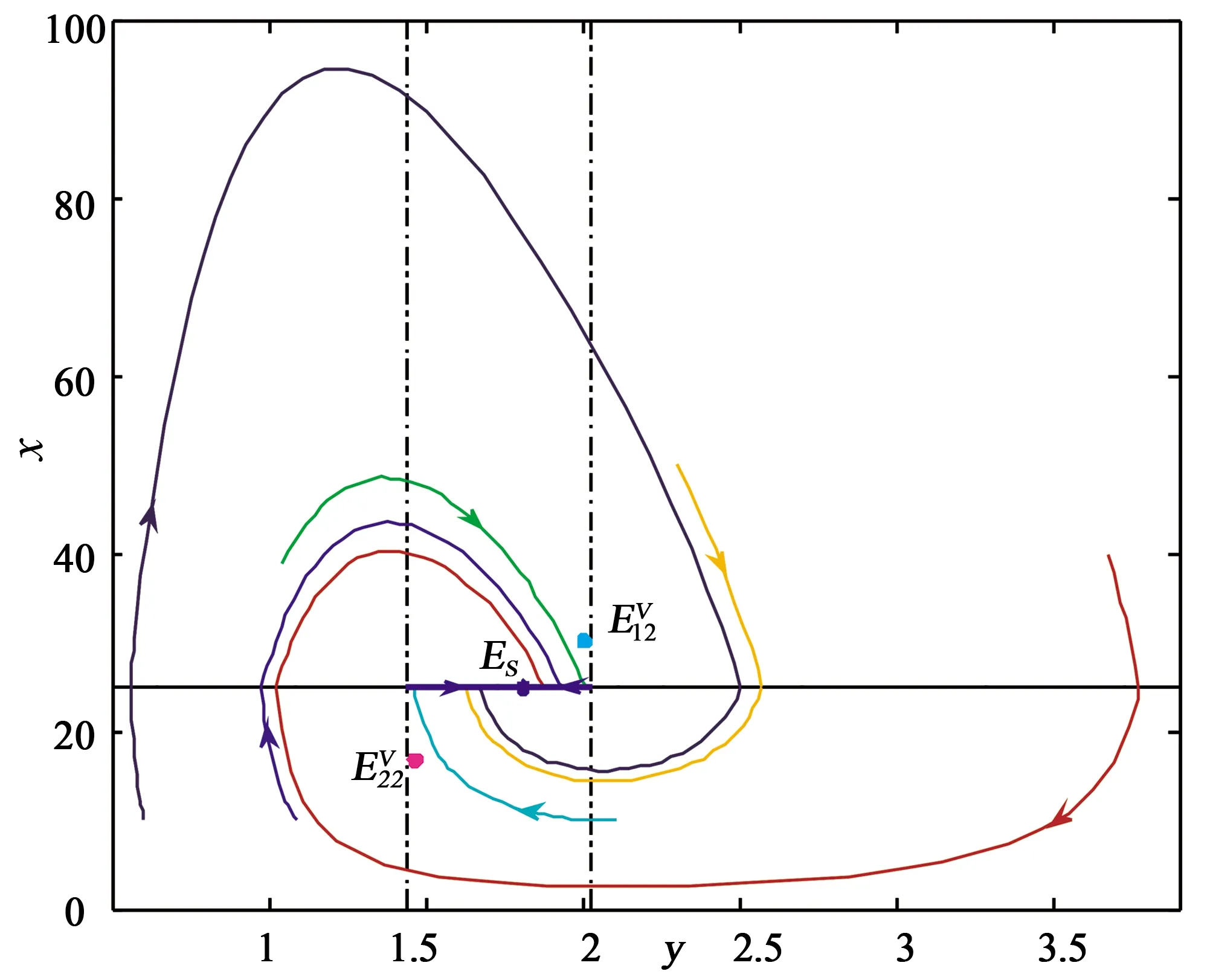
图3 Es全局渐进稳定

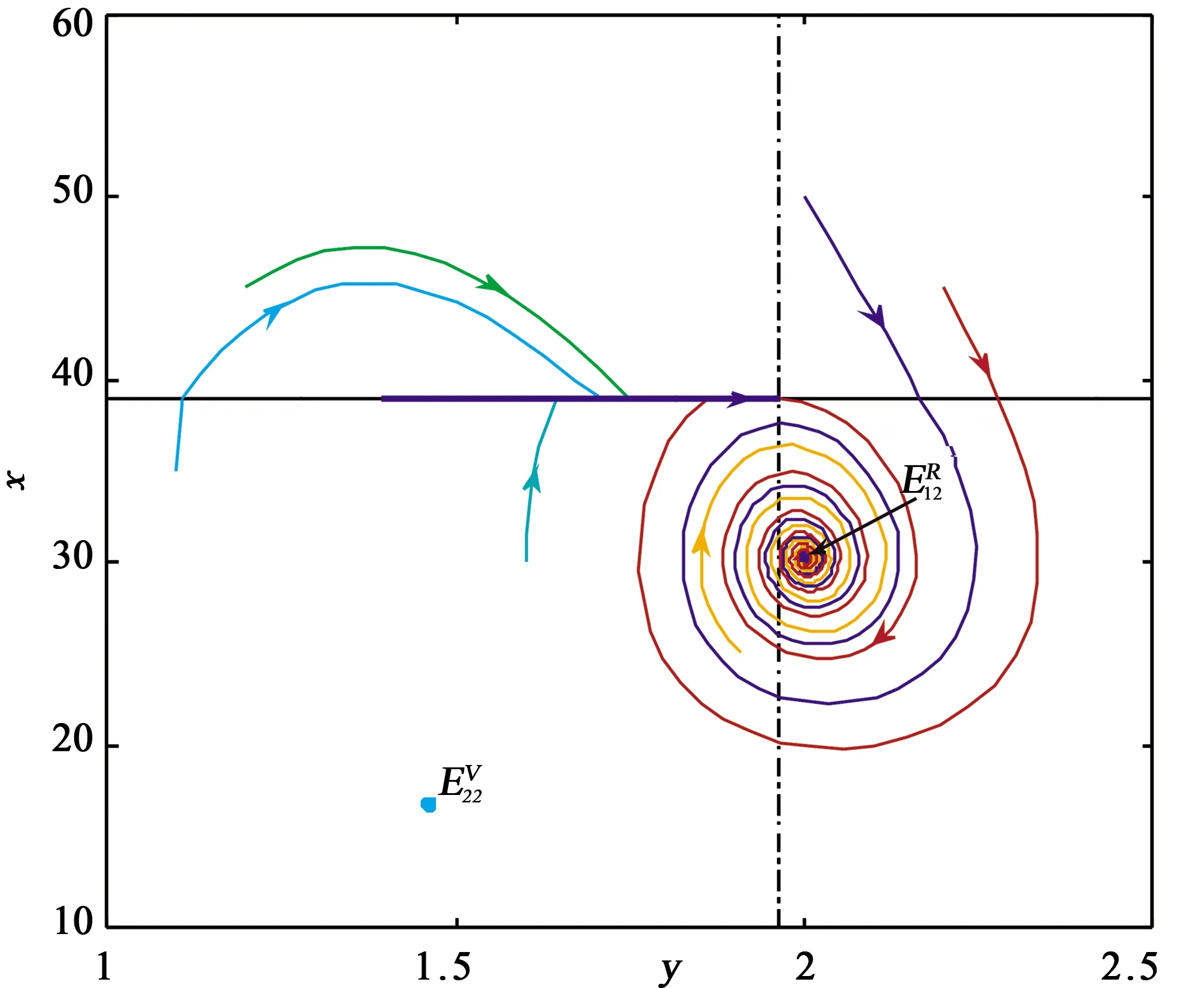
图全局渐进稳定

5 结 语

本文研究了具有logistic模型和HollingⅡ型函数的肿瘤免疫反应的Filippov模型,由捕食与被捕食模型原理,得到了子系统正平衡点的稳定性以及滑动系统伪平衡点的稳定性.研究了阈值策略下的免疫治疗对肿瘤免疫反应的作用和不同阈值下系统的全局稳定性,并通过数值模拟对系统全局动力学进行了分析.结果表明,基于阈值取值的不同,带有阈值策略的免疫治疗不仅可以控制肿瘤细胞数量而且增强了免疫系统的活性,相同的免疫治疗效应会使系统有不同的平衡解,系统的解最终稳定在子系统的真平衡点或者滑动系统的伪平衡点.