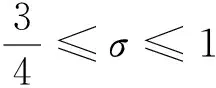Riemann Zeta函数零点分布的研究进展
张德瑜 黄 敬 张 芮
(山东师范大学数学与统计学院,250358,济南)
1 引 言
1859年, Bernhard Riemann 发表了一篇题为“Über die Anzahl der Primzahlen unter einer gegebenen Grösse (论不大于一个给定值的素数的个数)”的论文[1], 这是他唯一公开发表的数论文章. 然而, 正是这篇不长的论文开创了解析数论的一个新时期, 并推动了复变函数理论的发展. 众所周知, 著名的Euler恒等式:对实数s>1, 有
(1)
将素数p和自然数n联系了起来. Riemann 以Euler 恒等式作为研究的出发点, 将s看作复变数, 引入了复变数s=σ+it的函数
(2)
现在称它为Riemann Zeta函数. Riemann 对Zeta函数进行了非常深刻的研究, 将ζ(s)解析开拓到全平面, 证明了函数方程, 讨论了其零点等等. 更为重要的是,Riemann不但给出了新方法, 还提出了一个具有深远影响的天才猜测—Riemann猜想. 事实证明, 解析数论的中心问题—素数定理正是严格地按照Riemann的文章所提出的思想、方法和结论取得进展, 解析数论也沿着Riemann所指明的方向在二十世纪取得了迅速的发展.
本文中,将结合对Riemann Zeta函数的性质的了解与认知, 简要阐述Riemann Zeta函数的零点分布问题在当前的研究进展与研究动态. 在本文第二节,将简要阐述Riemann Zeta函数的解析性质:函数方程、非零区域、阶的估计、积分均值等. 第三节主要介绍Riemann Zeta函数的零点分布结果的研究进展. 第四节以Ingham的经典零点密度的结果为例, 简述了零点探测的方法. 最后一节为研究展望,介绍了Riemann Zeta函数的高阶推广—自守L-函数的零点分布的研究动态,其中包括作者近年来的部分工作.
2 Riemann Zeta函数的性质
从无穷乘积展开式(1),可以得到
|ζ(s)|>0,σ>1.
对(2)式利用部分求和公式,有
(3)
这里[u]表示u的整数部分, 上式中的积分当σ>0时绝对收敛, 因此Riemann Zeta函数在σ>0半平面上除去在s=1处留数为1的单极点外解析.
Riemann用两种方法(复变积分法、Poisson求和法)将ζ(s)开拓到整个复平面,令
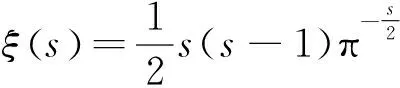
(4)
则ξ(s)满足函数方程
ξ(1-s)=ξ(s),
(5)
函数ξ(s)是一阶整函数, 由有穷阶整函数理论,可得到ξ(s)的无穷乘积表示:
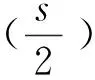
(i)ζ(s)有无穷多个非显然零点;
(ii) Imρ≠0, 即全为复零点;
(iii) 0≤β≤1;
(v) ∑|ρ|-1发散,而∑ρ-1-ε收敛,ε为任意正数.
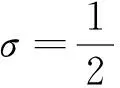
Riemann Zeta 函数的零点分布与素数分布紧密相连,连接的纽带则是下面的显式:
(6)
这里ρ取遍 Riemann Zeta函数的所有非显然零点.若Riemann猜想成立,则
(7)
1896年, J Hadamard和C J de la Vallée Poussin同时独立证明了在直线σ=1上ζ(s)≠0,且存在绝对常数c,使得在区域
(8)
中没有零点.此结果后来被Vinogradov和Korobov改进为
(9)
(10)
另外,Riemann Zeta 函数的阶的估计是数论学家关心的热点问题. 由(1)式, 显然, 当σ≥1+δ>1时ζ(s)≪1.
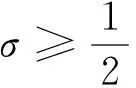

(11)
定义满足ζ(s)≪|t|c的c的下界为μ(σ). 根据Phragmén-Lindelöf原则, 知μ(σ)连续, 非负, 非增且下凸. 因此
(12)
由凸性,可以得到
(13)
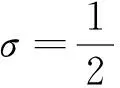
即
(14)
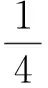
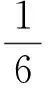
(15)
另一方面,可以考虑平均意义下的Lindenlöf猜想:
(16)
这里k为任意正整数. Littlewood证明了k=1时,
(17)
Hardy和Littlewood进一步证明了k=2时,
(18)
Heath-Brown[2]和Iwaniec[3]分别研究了小区间上的四次积分均值:
(19)

3 Riemann Zeta函数的零点分布
由于 Riemann Zeta函数的非显然零点对实轴对称且不为实数, 所以在讨论零点个数时, 可假定T≥0, 以N(T)表示在矩形0≤σ≤1,0≤t≤T中的ζ(s)的零点个数, 则
N(T+1)-N(T)≪log(T+2).
(20)
对T≥2, 有
N(T)≪TlogT.
(21)
更准确地说,N(T)有下面的渐近公式[4]:
(22)
这里
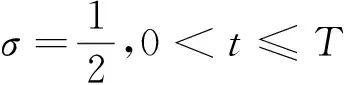
N(T)=N0(T),T>0.
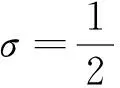
1921年,Hardy和Littlewood[6]证明了:存在正常数A1, 使得N0(T)>A1T.
1942年, A Selberg[7]取得了重大进展, 证明了存在正常数A2, 使得N0(T)>A2N(T).
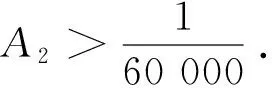
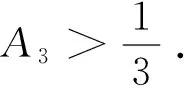
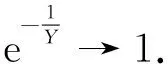
后来, 许多数学家对证明简化, 并改进了这个结果[10-15]. 另一方面, 大量的数值计算都支持猜想是正确的. 从1903年J P Gram计算了ζ(s)开头的15个零点起, 到1983年为止, Brent、Lune[16]等人证明了N(T)=N0(T),0 在Riemann猜想没有被证明的情况下,很自然而然地要去考虑有多少零点位于临界直线外. 因此, 令N(σ,T)表示ζ(s)在区域σ≤β≤1,|γ|≤T中零点ρ=β+iγ的个数,就是所谓的零点密度问题. 我们主要寻求如下形式的上界估计: (23) 证明上述形式的结果主要有两种方法. 一种是基于单复变函数论的Littlewood定理, 即利用幅角的变化来估计零点的个数, 并要用到凸性定理. 另一种方法本质上是由Linnik提出来的, 它基于这样一个事实:对应于每个零点, 总有一个Dirichlet多项式取“大值”. 因此, 利用Dirichlet多项式的均值估计就可相应得到零点个数的这种估计式.1940年, Ingham[17]证明了 (24) Huxley[18]得到 (25) 从上述结果可以得到 (26) 所以,零点密度猜想可以表示为 本节中将介绍零点密度估计的方法—零点探测法,进而得到Ingham的结果(24). 令 这里μ(n)为Möbius函数,且s=σ+it,log2T≤|t|≤T,X=X(T),Y=Y(T)为待定的参数. 由初等关系式 知 (27) 其中 得 结合(27)式,可得 (28) 这里ρ=β+iγ为ζ(s)的非显然零点. 其中当|v|≥log2T时,极点ω=1-ρ处的留数为o(1). 注意到,当Y→时 或 分别设R1,R2为满足(Ι)式、(ΙΙ)式的零点ρ=β+iγ的个数,且|γ1-γ2|≥2log4T. 因此 N(σ,T)≪(R1+R2+1)log5T. 一般来说,取X=Tε,则 对条件(Ι)中的和式利用二分法,设Tε≤N≤2-jYlog2Y,j=1,2,…, 则(Ι)中的零点个数为O(logY)个,满足(29)式的零点之和 (29) 将(29)式提升至k重和,得到 (30) 这里 其中k为依赖于N的自然数,使得 Nk=M,(2N)k=P≤Tc,P≪M. 将和式(30)分成长度为M的子和,取k使得 Nk≤Yrlog2rY 这里r为固定的整数,则(30)式变为 (31) 且 选取r=2,得 (32) 对(31)式利用分部求和,得 令 b(n)=0,u 则 ≪Tε(T+M)M1-2σ. (33) 下面估计R2. 令r=1,2,…,R2,且tr=γr+v', 这里γ1,γ2,…,γR2为满足条件(ΙΙ)的零点的虚部. 则由(ΙΙ)知 对r≠s,显然有|tr-ts|≥log4T,则 (34) 这里用到了ζ函数的均值估计 取 结合(33)和(34)式,可以得到 早在1859年,Riemann 在其题为“论不超过一个给定值的素数个数”的著名文献中第一次系统而又深刻的研究了素数分布与Riemann Zeta函数的复零点的分布之间的关系,为研究素数定理指明了方向. 正是沿着 Riemann所指出的方向, Hadamard 和 de la Vallee Poussin在1896年利用Zeta函数的非零区域证明了素数定理. 后来, Ingham,Huxley等数学家利用Zeta 函数的零点密度估计研究了小区间中的素数分布[34-38]. 研究各种各样的素数分布问题,一直是数论学家们关心的热点.20世纪九十年代,李红泽[39]研究了小区间中的殆素数,贾朝华[40]利用筛法研究了几乎所有小区间中的素数分布.Linnik[41]应用大筛法型的零点密度研究了算术级数中的最小素数问题,得到了和广义Riemann猜想下相同的结果. 后来,陈景润、王天泽[42]给出了算术数列中素数分布的一个定理,为Goldbach猜想的证明奠定了基础. 最近,在自守L-函数方面,刘建亚、叶扬波[43]将自守L-函数的零点分布的结果用于素数理论,在适当的假设下证明了Linnik常数等于1,这冲破了GL(1)的Riemann猜想的限制. Piatetski-Shapiro素数定理指的是存在c>1,使得有无穷多形如[n^c]的素数. 它是数论中非常重要的定理之一. 许多数论学家如Piatetski-Shapiro,Balog,Frielander, 贾朝华, 李红泽等都对这一问题做了相关研究[44-47],得到了若干结果. 后来,S Baier 和Zhao L Y[48]研究了SL_2(Z)上Hecke特征值在Paiertetski-Shapiro 素数中的分布,进一步完善了SL_2(Z)上自守L-函数的解析理论. Balog[49]和G Dufner[50]首次给出了Piatetski-Shapiro孪生素数的定义,并研究了其平均分布. 最近,张德瑜和翟文广利用自守L-函数的零点密度证明了SL_2(Z)上全纯尖形式的傅里叶系数在Piatetski-Shapiro孪生素数中的均值定理. 自守L-函数理论是目前数论、代数、调和分析和几何学等学科交汇点上的热点领域, 这个领域既包含着解决数学问题的重大潜力(例如,费尔马大定理的证明);也包含着许多迷人的猜想,其中居于核心地位的是广义Riemann猜想,即自守L-函数的非显然零点都位于Res=1/2这一临界直线上. 在广义Riemann猜想还没有被证明的情况下,我们很自然地去考虑自守L-函数有多少零点落于临界直线之外, 即考虑关于自守L-函数的零点密度问题. 零点密度问题在研究小区间素数分布、稀疏素数分布等问题中会起到类似于Riemann 猜想的作用. 因此,对零点密度的研究, 为我们提供了一个研究素数分布问题的有效工具与手段. 但由于自守L-函数的代数及几何性质理论较复杂, 给相应的问题计算带来了巨大困难与前所未有的挑战. 现在的研究工作仅仅是个开始, 仍需要数论学界高度关注与深入研究.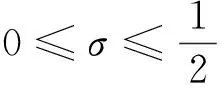
4 零点探测法

5 研究展望