动态域上不连续动力系统的理论及方法

傅希林

(山东师范大学数学与统计学院，250358，济南)

1 引 言

不连续动力系统是从动力学角度描述刻划客观现实中相互作用的若干物体的动力学模型.现实世界中大量实际问题的研究对象往往不是单一、静止、孤立的，而是多个、动态、相互作用的.具有这样特征的实际问题数学模型往往可归结为不连续动力系统.

不连续动力系统是这样的动力系统：一般而言，在不同区域或不同时间区间上存在不同的连续子系统，且不同的连续子系统的动力学性态都是不同的.从相互作用、动态、统一的观点将各个不同区域或不同时间区间上存在的连续子系统，连同各不同区域边界的特性(譬如边界约束条件)或不同时间区间端点的特性(譬如传输率)一起，整体看作动态域上的不连续动力系统.

1.1实际意义大量机械工程中的实际问题(譬如碰撞问题、摩擦问题、连接问题、悬挂问题等)的数学模型往往可以用“不连续动力系统”来描述.滑模控制的大量实际问题(譬如同步问题、导弹跟踪问题、航天器列队飞行问题等)的数学模型往往可归结为含有某种控制律的不连续动力系统.

许多实际问题的数学模型可以归结为这样一类具有切换时刻的切换动力系统：有限个子系统在无限个时间区间上进行切换，而在切换时刻(区间端点)满足传输律.从不连续动力系统的角度来看，这类切换动力系统实质上是一类具体的具时间切换的不连续动力系统.

具有瞬时突变现象的实际问题的数学模型往往可以归结为具体的脉冲微分系统.根据脉冲微分系统理论[1]，脉冲微分系统常见类型有两类：一类是具有固定时刻脉冲的脉冲微分系统，其特点是脉冲时刻与状态无关.这类脉冲微分系统实质上是一类以脉冲时刻为切换时刻的具时间切换的不连续动力系统.另一类是具有任意时刻脉冲的脉冲微分系统，其特点是脉冲面依赖于状态.这类脉冲微分系统实质上是一类以脉冲面为边界的具边界转换的不连续动力系统.因此从不连续动力系统的角度来看，具有瞬时突变现象的实际问题的数学模型往往可以归结为具体的不连续动力系统.

近年来关于多自主体系统的研究受到广泛关注，形成了研究的热点问题.自主体是具有一定独特性特征各自可识别的多单元系统的个体；所谓多自主体系统就是含有多个自主体的集合或群体，它是一个有一定规则和秩序的群体，它能够完成群体内单个个体不能完成的、比较复杂或艰巨的任务.研究表明，多自主体系统已成功应用于太空卫星群运行、信息网络拥塞、无人飞机的协同、机器人队列控制、网络游戏设计以及人群行为模拟等实际问题.从不连续动力系统的角度来看，多自主体系统实质上是以各个自主体为子系统的不连续动力系统.

1.2历史纵观现从历史的角度纵观不连续动力系统研究所经历的自然过程.这里仅指出不连续动力系统研究的基本背景和几个关键趋势，而不是提供其详细的历史.可以认为，关于不连续动力系统的研究迄今已经历了3次发展浪潮.

不连续动力系统研究的历史可以追朔到20世纪30年代.在机械工程中基于“碰撞”或“摩擦”的不连续动力系统实际问题是普遍存在的.对这些问题的动力学研究是机械工程研究领域最基本且又最重要的问题.1931年den Hartog[2]研究了具有摩擦的、含有强迫外力的阻尼线性振子的周期运动.1932年den Hartog和MiKina[3]使用固定域上无阻尼的分段线性系统来研究齿轮啮合动力学.1949年Levinson[4]用分段线性模型研究了具有周期激励的VdP方程的周期运动.1988年Ozguven和Houser[5]用分段线性模型和碰撞模型来描述和研究啮合力学模型.1991年Nordmark[6]使用术语“擦边”对一个具体碰撞振子的擦边现象进行了描述并给出了擦边条件.1998年Natsiavas[7]研究了含有三个对称线性弹簧的分段线性系统的稳定性和周期分支.这些关于机械工程中的不连续动力系统实际问题的前期研究工作都是在固定域上进行的，大多是化作分段线性系统用连续动力系统的方法进行研究，但是关于不连续边界上流的奇异性分析不够充分.

20世纪60年代不连续动力系统研究的第二次浪潮很大程度上是伴随着“微分包含”、“极值函数”概念的形成与相应非光滑理论的出现而掀起的.1964年Filippov[8]将库仑(Coulomb)摩擦振子模型视为右端不连续的微分方程，通过引入“微分包含”和“极值函数”方法，研究了该系统不连续边界的滑模运动，并讨论了这类不连续动力系统(非光滑系统可以看作是一类具体的不连续动力系统)解的存在性和唯一性.1974年Aizerman和Pyatniskii[9,10]拓展了Filippov的概念，提出了非光滑系统的一般理论.1976年Utkin[11]基于Filippov非光滑系统理论发展了动力系统的控制方法，即滑模控制.2000年Kunze M, Kupper T和Li Yong[12]给出了非光滑系统的Conley 指数定理，并应用此定理得到了关于非光滑系统全局分支的研究结果.2001年Huang Lihong等[13]阐述了右端不连续微分方程理论与应用，给出了具有不连续激励函数的神经网络模型及具有不连续特征的生物学模型的研究结果.2009年Liu X和Han Maoan[14]研究了非光滑Lienard系统的Hopf分支.2010年Han Maoan和Zhang Weinian[15]得到了非光滑planar系统的Hopf分支研究结果.这些工作的主要特点是突破了过去用连续动力系统的研究思想方法来研究不连续动力系统的局限，运用Filippov非光滑系统理论来研究右端不连续的不连续动力系统.但整体而言Filippov理论主要集中用于研究非光滑动力系统解的存在性与唯一性，且仍是在固定域上来考虑的.因此对于边界上流的奇异性尚需进一步研究.

脉冲微分系统作为一类具体的不连续动力系统,对其研究可以追朔到1960年Mil’man V D和Myshkis A D[16]的工作.自20世纪80年代对其研究日益活跃.1989年Lakshmikantham V,Bainov D D和Simeonov P S[17]总结了脉冲微分系统早期研究成果.国内也相继有学者着手这方面的研究.譬如中山大学的徐远通教授、山西大学的燕居让教授、中国海洋大学的张炳根教授、北京理工大学的葛渭高教授、清华大学的章梅荣教授、广州大学的庾建设教授、兰州大学的李万同教授、杭州师大的申建华教授、华中理工大学关志洪教授以及华南师大的翁佩萱教授等.1996年Yu Jianshe和Zhang Binggen[18]建立了一阶脉冲时滞微分方程3/2稳定性判别准则.2002年Liu Bing和Yu Jianshe[19]借助重合度延拓定理,得到了二阶脉冲微分系统m点边值问题解的存在性定理.1998年Shen Jianhua和Yan Jurang[20]得到了脉冲泛函微分方程Razumikhin型稳定性定理.1999年Fu Xilin, Qi Jiangang和Liu Yansheng[21]通过构造具有脉冲积分限的积分函数，给出了关于非线性脉冲微分系统周期轨存在的充要条件.2002年Lin Wei[22]研究了具有脉冲的Lorenz系统的Lorenz吸引子性态，并探讨了因脉冲影响所导致的该系统的复杂动力学现象.2008年Fu Xilin,Yan Baoqian和Liu Yansheng[23]总结了关于非线性脉冲时滞微分系统的阶段性研究成果，特别是给出了关于具无穷延滞的脉冲微分系统解的存在性、具实参数的脉冲自治微分系统奇点分类与分支的研究结果.整体来看前期关于脉冲微分系统研究的特点是：所用的方法主要还是基于研究连续系统的思想方法；所研究的脉冲微分系统侧重于研究具固定时刻脉冲情形；而对于具任意时刻脉冲的脉冲微分系统的研究，基本上还是局限于轨线对脉冲面碰且仅碰一次的特殊情形.

不连续动力系统研究的第三次浪潮始于2005年的突破.Luo A C J[24]在2005年出了动态域上不连续动力系统理论.2006年Luo A C J[25]及2008年Luo[26]对此理论又作了进一步凝练和提升.2007年Luo A C J和Thapa[27]运用不连续动力系统的流转换理论研究了在周期激励作用下刹车系统的非线性动力学行为.2009年 Luo A C J[28]将不连续动力系统的流转换理论用于“同步”的研究，得到了“弹簧”振动系统与“单摆”振动系统同步的充要条件.2012年Luo A C J[29]系统阐述了动态域上不连续动力系统理论的基本内容，搭建出动态域上不连续动力系统理论的基本架构.上述工作的特点是所考虑的不连续动力系统模型都是在动态域上来考虑的，都运用了“G函数”作为测度来“度量”不连续边界的奇异性，并运用流转换理论具体分析了边界上流的转换性；有些工作还运用映射动力学理论在“动态域”与“不连续”情形下研究了相应模型的周期运动.特别需要指出的是，近年Ni Mingkang[30]独辟蹊径,运用奇异摄动多尺度方法和空间对照结构理论得到了关于脉冲微分系统解的结构的创新结果.

同时，国际上一批动力系统专家学者近年也着手开展关于不连续动力系统的研究.俄罗斯院士、圣彼得堡大学的Gennady Leonov教授、墨西哥Autonoma 大学的Valentin Afraimovich教授、法国巴黎大学的Maurice Courbage教授、德国Bielefeld大学的Dimitry Volchenkov教授、美国Georgia Tech的Leonid Bunimovich教授、西班牙国王大学的Miguel A F S等都从不同角度对关于不连续动力系统的实际问题进行了研究.近5年关于不连续动力系统的国际会议已分别在美国、中国、土耳其、巴西、莫斯科召开.这些都充分说明关于不连续动力系统的研究在国际上已日益活跃，并逐渐形成研究热点.

1.3本文结构本文结构如下： 第2节分别给出具边界转换的不连续动力系统和具时间切换的不连续动力系统的基本概念;阐述了不连续动力系统的两个特征，指出其特征会对系统的动力学性态与规律往往会产生本质影响；并由此自然提出了关于动态域上不连续动力系统的动力学问题.第3节给出了动态域上不连续动力系统理论的基本架构，并分别阐述了该理论的基本内容：流转换理论和映射动力学.着重给出G函数的概念，并借助G函数在动边界任一点局部建立了相应的度量测度，从而能够将极限分析的思想方法用于分析研究动态边界上流的转换及奇异性.第4节介绍当前不连续动力系统研究的一些进展.

2 不连续动力系统动力学问题

通常有两类不连续动力系统[31]：一类称作具边界转换的不连续动力系统,是指在相空间中存在若干不同的区域,在任何两相邻区域上都分别定义着连续子系统；一旦子系统的流“抵达”相应区域的边界,两相邻子系统之间的差异,将通过边界上的流转换性来传达.另一类称作具时间切换的不连续动力系统,是指对于两相邻的不同的时间区间上对应有确定的动力系统；一旦动力系统的流“抵达”时间区间端点(切换时刻)，两相邻时间区间上动力系统的差异，将通过切换时刻的传输率来传达.

本节分别给出具边界转换的不连续动力系统和具时间切换的不连续动力系统的基本概念.

2.1具边界转换的不连续动力系统假设在第i个开的可接近子域Ωi(α∈{1,2,...，N})上, 存在一个Cri连续系统

(1)

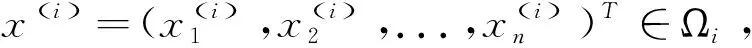
H1 两个相邻子系统之间流的转换关于时间t是连续的.

H2 假设一个可接近域 Ωi是无界的, 则存在一个开域Di⊂Ωi, 该子系统的向量场和流是有界的.也就是说, 在域Di内, 当t∈[0,)时, 存在两个常数K1和K2使得下列不等式

‖F(i)‖≤K1和‖Φ(i)‖≤K2

成立.

H3 假设一个可接近域Ωi是有界的, 则存在一个开域Di⊂Ωi, 该子系统的向量场有界, 但子系统的流可以无界. 也就是说, 在域Di内,当t∈[0,)时, 存在常数K1使得下列不等式

‖F(i)‖≤K1和‖Φ(i)‖<

成立.

为了构建不同子域之间流的动力学性质的相互联系, 对于可连通域的两个相邻可接近域Ωi与Ωj可以定义子域之间的边界.

(2)

其中边界约束函数φij是Cr(r≥1)连续的.

以边界为定义域, 相应动力系统记为

(3)

定义1[32]在相空间中, 对于定义在各个子域Ωi(i∈{1,2,...,N})内的连续系统(1)及定义在各个边界∂Ωij(i,j∈{1,2,...,N})上的边界系统(3), 在边界约束函数(2)的共同作用下形成一个整体不连续的动力系统, 且满足假设(H1)-(H3), 则称系统(1)-(3)为具边界转换的不连续动力系统.

作为不连续动力系统的特例, 具任意时刻脉冲的脉冲微分系统

(4)

就是一类具边界转换的不连续动力系统, 其中连续部分为各个子域内的连续动力系统, 依赖状态的脉冲面t=τ(x) 为边界约束函数, 而脉冲函数x(t+)=h(x(t))是边界系统的动力学方程.

2.2具时间切换的不连续动力系统若已知不连续动力系统在边界附近出现流的转换或切换的时刻, 则系统将在达到这些时刻时, 受边界系统的作用在若干连续子系统之间切换, 从而成为具时间切换的不连续动力系统. 切换系统即这种情形的典型例子, 其中传输率即边界系统, 切换时刻即发生流的转换或切换的时刻. 假设在第i个开子域Ωi(i=1,2,...m,m≤M)内, 存在一个区间[tk-1,tk] 上的Cri(ri≥1)连续系统

(5)

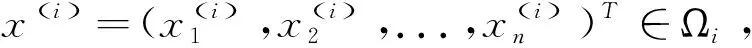
为了研究包含若干子系统(5)的具时间切换的不连续动力系统, 考虑下列假设:

H4 任意两个子系统之间流的切换关于时间t是连续的;

H5 在子域Ωi(i=1,2,...，m)内, 对t∈[tk-1,tk],

(6)

H6 在子域Ωi(i=1,2,...，m)内, 对t∈[tk-1,tk],

(7)

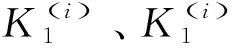
H7 对t∈[tk-1,tk],

(8)

其中∂Ωi为开子域Ωi的边界, 可以看作

(9)

在假设H6下, 第i个子系统的任意流在t∈(tk-1,tk)上, 即切换至相邻子系统之前, 不会达到边界, 否则可按照前面的具边界转换的不连续动力系统讨论. 通过上述假设, 相应子系统在有限时间区间上存在有限解, 从而可进一步讨论具时间切换的不连续动力系统的定义.

为了讨论切换系统的动力学行为, 首先给出有限切换时间区间上的连续动力系统集合的概念.

定义2[33]对于动力系统(5), 假设系统流发生切换的时刻为tk(k∈Z+), 在子域Ωi(i=1,2,...，m)内区间[tk-1,tk]上的动力系统集合为

={Si|i=1,2,...,m},

(10)

其中

基于上述定义, 考虑第i个动力系统Si对应的相空间, 即 第i个子空间为

(11)

由此可以将系统的相空间划分为依赖切换时刻tk的若干子空间及其之间的边界

(12)

为了研究切换系统在任意两个子空间之间流的切换问题, 首先基于具时间切换的不连续动力系统相邻两个子空间的上述两种关系, 介绍两种流的连续切换的定义并给出传输率的概念.

定义3[34]考虑动力系统集合(10)中的任意两个动力系统Si,Sj, 对应子域为Ωi,Ωj,

则称系统Si与Sj在tk是Cr-连续切换的;

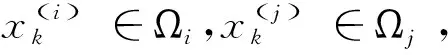
(13)

则称系统Si与Sj在tk是C0-连续切换的. 由此, 根据不同时间区间上流的切换, 可以给出具时间切换的不连续动力系统的定义.

定义4[34]考虑相空间的一个划分(12), 对于定义在子空间(11)上的连续系统

(14)

(15)

的作用下若干(14)式形成一个整体不连续的动力系统, 且满足假设(H4)-(H6),则称系统(14)-(15)为具时间切换的不连续动力系统.

作为不连续动力系统的特例,具固定时刻脉冲的脉冲微分系统

属于具时间切换的不连续动力系统, 其中由脉冲面函数解出的固定的脉冲时刻tk即切换时刻.

2.3不连续动力系统动力学问题不连续动力系统有两个特征：其一是所考虑的不连续动力系统具有随时间变化的定义域.其二是所考虑的不连续动力系统具有关于边界或切换时刻的不连续性.不同区域或不同区间上的动力系统不同，整体不连续.这种不连续性特别体现在边界上、切换时刻处.

不连续动力系统的“动态域”与“不连续”特征对系统的动力学性态与规律往往会产生本质影响，导致系统发生复杂动力学行为.尤其是具边界转换的不连续动力系统在相邻区域共同边界的转换状态、具时间切换的不连续动力系统在切换时刻的切换状态都往往会出现不连续动力系统所特有的复杂动力学行为.主要体现在如下三个方面：

第一方面，体现在由不连续动力系统的“动态域”与“不连续”特征所导致的流转换或流切换的复杂性.譬如不连续动力系统边界上可以出现可穿越流、不可穿越流、滑模流、擦边流等；进一步研究还揭示了该系统临界滑模运动发生裂碎的复杂动力学现象[35].

第二方面，体现在由不连续动力系统的“动态域”与“不连续”特征所导致的周期运动的复杂性.文献[36]说明在不连续动力系统周期流的研究中，会出现所谓的分支树及复杂动力学现象.文献[37]揭示了所考虑的不连续动力系统振子模型两独立的周期运动之间存在混沌运动或大幅跳跃现象.

第三方面，体现在由不连续动力系统的“动态域”与“不连续”特征所导致的新的分支与碎裂.譬如对于具边界转换的不连续动力系统，可以出现穿越流滑模分支和穿越流的源分支，亦可以出现非穿越流的滑模碎裂分支和非穿越流的源碎裂分支[29].这些所谓的“转换分支”都是具边界转换的不连续动力系统在其边界上流转换过程中所特有的分支现象；这里所谓的“碎裂”就是由分支引起的复杂动力学现象.

因此，由不连续动力系统自身特征必然导致其动力学研究的新困难.一方面是由“动态域”所带来的新困难.由于“区域”或“区间”都是时变的，相应的“边界”或“切换时刻”也是时变的.这种时变千变万化，没有一般规律，只能根据实际问题的具体特征而定.另一方面是由“不连续”所带来的新困难.对不连续动力系统来说，尽管其局部在“不同区域”或“不同区间”上通常都有连续子系统，但就整体而言系统是不连续的，这种不连续性往往导致在“边界”或“切换时刻”流的奇异性.已有研究表明不连续动力系统在“边界”或“切换时刻”流的奇异性主要有如下呈现：流的性态在“边界”或“切换时刻”附近的复杂多样性; 流的结构在“边界”或“切换时刻”附近的深度隐蔽性; 流的趋势在“边界”或“切换时刻”附近的集合吸引性.

根据上述分析，我们可以自然提出关于动态域上不连续动力系统研究的基本动力学问题：揭示在“动态域”与“不连续”情形下不连续动力系统流的奇异性规律；寻求在“动态域”与“不连续”情形下不连续动力系统周期运动的特性；探讨在“动态域”与“不连续”情形下不连续动力系统新的分支性态及复杂动力学行为.

需特别指出的是，这里所考虑的动态域上由多个连续子系统组成的不连续动力系统通常不满足Lipschitz条件.众所周知，动力系统的存在唯一性定理等基本理论都是基于Lipschitz条件的，并且基于Lipschitz条件的动力系统基本理论也被大量应用于工程与科技诸领域.但是Lipschitz条件的假设对于不连续动力系统实际问题而言往往是太强了，致使连续动力系统的传统理论在此就不能应用.甚至当试图将连续动力系统的传统研究方法用于不连续动力系统时也难以奏效，且往往使问题的解决变得更加复杂和困难.因此基于Lipschitz条件来建立不连续动力系统的动力学基本理论是难以行得通的.

对不连续动力系统从理论上进行研究主要在如下两个方面具有重要科学意义.一方面，紧紧围绕不连续动力系统的基本动力学问题开展研究，探讨不连续动力系统动力学行为的规律与特征.另一方面，对不连续动力系统的研究必须探索新的研究方法.过去用于连续动力系统的研究思想和方法已受制约，或已不再适用，都需要另辟蹊径，寻求新的研究方法与途径.因此开展对不连续动力系统动力学问题的研究，对于探索研究不连续动力系统的新途径、寻求不连续动力系统的自身客观规律、揭示不连续动力系统的本质等都具有重要的科学意义.

3 动态域上不连续动力系统理论

动态域上不连续动力系统理论正是在不连续动力系统前期研究的基础上，顺应不连续动力系统研究的历史趋势，着眼于层出不穷的当代实际问题的挑战而产生的.动态域上不连续动力系统理论的基本架构是：以不连续动力系统流转换理论和不连续动力系统映射动力学为基本内容；并由其自然派生拓展出不连续动力系统流转换分支理论、不连续动力系统流障碍理论、不连续动力系统多值向量场理论及n-维不连续动力系统棱转换理论等，搭建出动态域上不连续动力系统理论的基本架构[33].

本节着重介绍动态域上不连续动力系统流转换理论和不连续动力系统映射动力学.

3.1不连续动力系统流转换理论作为动态域上不连续动力系统理论的基本内容之一的流转换理论的基本思想是：受物理能量层启发，针对不连续动力系统动边界提出了“G函数”的概念，并用G函数作为度量测度，给出了不连续动力系统不连续边界上各类流转换的解析条件，有效克服了不连续动力系统自身的“动态域”、“不连续”所带来的本质困难.

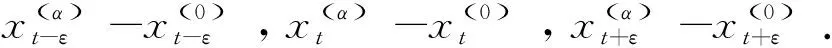
其中在t时刻边界 ∂Ωij上x(0)(t)处相应的法向量为

(16)

如果此刻的法向量是单位向量,则位移向量差和法向量的乘积就是位移向量差在法方向上的投影.因此区域内的流与边界流的差在法方向上的变化率是度量区域内的流与边界流关系的重要指标,是研究的重点.下面首先阐述G函数的概念.

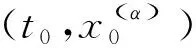
(17)

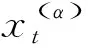
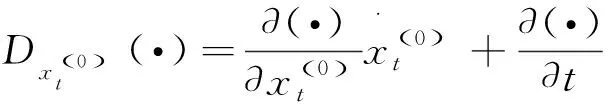
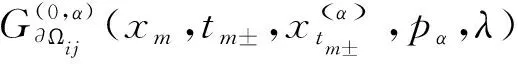
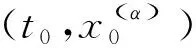
再次对上述方程进行Taylor级数展开, 得到如下表达式

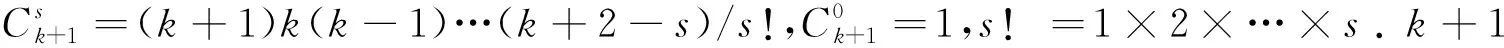
为更好地理解G函数的概念, 下面通过具体例子进行说明. 取具有扰动的二维非线性Hamilton系统

(18)

其中两个参数满足μ∈Rm1,π∈Rm2. 对应的无扰动的Hamilton系统为

(19)

根据能量守恒, 无扰动Hamilton系统关于时间的变化率为0, 即有以下关系:

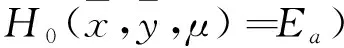
扰动向量场为

F(x,y,t,p)=(F1(x,y,t,p),F2(x,y,t,p))T.

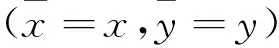
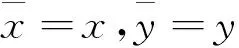
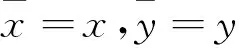
其中全微分为(σ=1,2)

由定义可知, 一阶G函数是零阶G函数关于时间的变化率. 换句话说, 一阶G函数是扰动向量场在Hamilton能量曲面法方向上的分量关于时间的变化率.

通过上述具体例子的分析, 我们对G函数的概念进行了进一步的阐述, 并具体给出了零阶G函数和一阶G函数的表达形式, 这有助于对G函数的深刻理解.

定义7[33]考虑不连续动力系统(1)-(3),tm时刻在两个相邻区域Ωα(α=i,j) 的边界∂Ωij上点为x(0)(tm)=xm∈∂Ωij. 对任意ε>0, 存在时间区间[tm-ε,tm).假设fx(α)(tm-)=xm. 如果两个区域内的流x(α)(t)(α=i,j)满足如下性质

则称两个流x(i)(t)和x(j)(t)关于边界∂Ωij是第一类不可穿越流(汇流).

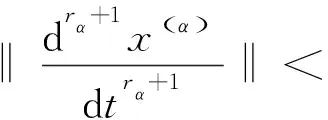
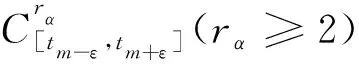
则称区域Ωα内的流x(α)(t)是相切于边界∂Ωij的相切流(擦边流).

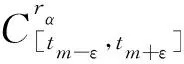
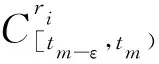
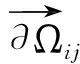
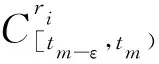
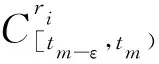
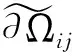
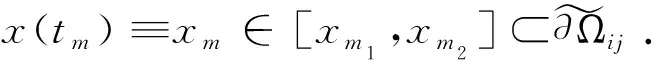
3.2不连续动力系统映射动力学动态域上不连续动力系统理论的另一基本内容是不连续动力系统的映射动力学.其基本思想是：将动力系统符号动力学的思想应用于不连续动力系统，针对各类不连续动力系统“边界”或“切换时刻”的特征构造相应的基本映射，再通过基本映射的复合得到相应的映射结构，进而可以研究不连续动力系统周期流的存在性、稳定性及分支，也有效克服了不连续动力系统自身的“动态域”、“不连续边界”所带来的本质困难.下面具体介绍具时间切换的不连续动力系统的映射动力学.

对于具时间切换的不连续动力系统, 其切换时刻为固定的时间序列, 相应转换点集合及基本映射均可借助切换时刻的信息给出.首先由切换时刻给出所对应的转换点集合的概念.

定义11[38]假设不连续动力系统(14)-(15)的流的切换时刻为tk(k∈Z+), 那么对第i个子空间Ωi而言, 第i个转换集定义为

(20)

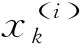
1) 对于区间[tk-1,tk], 在子空间Ωi内关于系统(14)-(15)的转换集Ξ(i)的域内映射为

2) 在切换时刻tk, 关于系统(14)-(15)的相邻两个转换集Ξ(i)和Ξ(i+1)的传输映射为

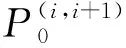
这两类基本映射的控制方程可由连续部分的动力系统和切换部分的传输率得到.在切换时刻tk,对于相邻两转换集上的传输映射P0,由传输率(13)可得到基本局部传输映射的控制方程为

(21)

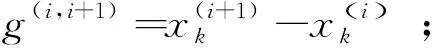
(22)

在区间[tk-1,tk]上, 对于连续子空间内的连续基本映射Pi, 应用子系统上的方程(5)知, 基本局部域内映射的控制方程为

(23)

在给出具时间切换的不连续动力系统的一般运动的映射结构之前, 首先针对连续切换的两种情形统一给出元映射的概念.

基于上述基本离散映射的构造, 针对所研究的具时间切换的不连续动力系统这一整体不连续系统, 对于区间[tk,tk+1], 可以得到一个在相邻两个转换集之间的局部元映射

(24)

其中

P(i,i+1)=(P0)λ°Pi+1,λ∈{0,1}.

(25)

当λ=1时,P(i,i+1)=P0°Pi+1包含了流的连续部分和一次C0-连续切换,表示从子空间Ωi到Ωi+1在区间[tk,tk+1]上的一个完整映射;当λ=0时,P(i,i+1)=Pi+1仅包含了流的连续部分,但流在tk+1时刻达到子空间Ωi和Ωi+1的重合部分,在区间[tk,tk+1] 上实现了一次Cr-连续切换.

对于每个单位区间[tk,tk+1]上的元映射,其控制方程可由基本映射的控制方程(21)-(23)复合得到.

经多次复合之后, 可由每个子空间单元内的元映射(24)-(25)得到推广意义下的一般映射结构

(26)

其中

(27)

且λis∈{0,1},ij∈{1,2,...,m-1},j=1,2,…,s.

在一般映射(26)-(27)中, 上标(i1,i2,...,is,is+1)表示该全局映射是从转换集Ξ(i1)上开始的s个不同的元映射P(ij,ij+1)(j=1,2,...s)的复合映射, 最终映射到转换集Ξ(is+1)上, 刻画了区间[tk1,tks+1]上的系统流的全局动态行为. 该映射结构的Jacobi矩阵及映射动力学的定性分析将在下面以周期运动为例具体给出.

根据映射动力学的理论, 在不考虑局部信息时, 对于具时间切换的不连续动力系统(14)-(15)所对应的任意流均可以由前面给出的一般映射来刻画. 为了分析并预测系统的周期运动的动力学行为, 在映射意义下, 首先给出所研究的具时间切换的不连续动力系统(14)-(15)的周期流的概念.

(28)

且

tkm-tk0≡T,

(29)

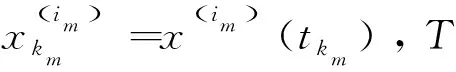
若系统流满足

(30)

且

tlkm-tk0≡lT,

(31)

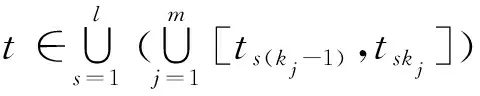
对于周期运动的一般映射结构, 其转换集可以通过一系列非线性代数方程组确定. 考虑前面给出的一般映射结构P(i0,i1,...,im), 由定义12可知其 映射关系为

(32)

该映射由如下基本映射关系

(33)

复合而成, 其中元映射P(is,is+1)=(P0)λis°Pis,s=0,1,...m-1,λis∈{0,1}. 由于(21)可以描述两类连续切换的传输映射的控制方程, 故可取λis=1, 即对每个元映射P(is,is+1)而言, 映射关系为

(34)

考虑(33)-(34)中每一个映射的起点和终点, 可由(21)及(23)得到映射(32)的2m个代数控制方程

(35)

注1在定义12中, (30)-(31)说明该周期流的切换时间关于初始转换集具有等时差性, 即Luo[3]所讨论的具等时切换的不连续动力系统在一般映射结构下的周期运动, 此种特殊情形在实际应用中具有重要的现实意义.

对于系统(14)-(15)在映射意义下的一般周期流的解析条件, 可以通过求解条件(28)和(29)得到. 一旦得到周期运动在相应碰撞点的解析条件, 那么此周期流在转换集附近的局部稳定性可以通过传统判断局部稳定性的方法进行分析判断.

下面借助前面的离散映射和不连续动力系统的基本理论,介绍所研究的具时间切换的不连续动力系统(14)-(15)的周期运动的动力学分析结果, 采用广义特征值理论总结系统周期流各种不同的动力学行为以及解析预测,包括周期流的稳定性条件和分支条件.

定理5[39]对于具时间切换的不连续动力系统(14)-(15),考虑其基于切换时刻tkj(j∈{0,1,...,m})的相空间的划分(12),若存在满足条件(28)和(29)的周期运动,则其局部稳定性分析可由广义特征值理论得到.

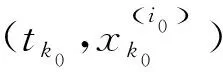
其中元映射

并可由参数

αkj+1=tkj+1-tkj

(36)

表示该元映射的区间长度.

由映射关系(33)-(34)可以得到包含了两类连续切换的每个切换点处的映射

其中每一个映射对应一个代数控制方程,则映射P的2m个代数控制方程可由(35) 确定.由周期流的定义,条件(28)中im=i0,从而由(35)可解得该周期流的相应切换点,将切换时刻代入(36)后,可以由

计算出该周期流的周期T,同时得到切换时刻区间参数

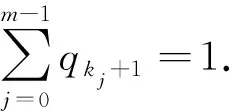
因此,在整个区间[tk0,tk0+T]上,系统(14)-(15)在全局映射下的流可以表示为

(37)

为了确定系统的周期运动的稳定性,首先需要确定总映射P的Jacobi矩阵,然后根据其特征值,分析系统的周期解的局部稳定性和分支问题.对于周期运动(37),其相应的Jacobi矩阵为

(38)

上式中两个基本离散映射的Jacobi矩阵的元素可以各自通过方程(21)和(23)按如下方式计算：

(39)

(40)

其中j=0,1,...，m-1.

将各个映射的Jacobi矩阵元素(39)和(40)代入总映射P的Jacobi矩阵(38), 由

|DP-λI|=0

可以计算出周期运动映射结构的特征值λ1,λ2.记矩阵DP的秩为Tr(DP),行列式为 Det(DP),则DP的特征值可表示为

(41)

其中 △=[Tr(DP)]2-4Det(DP).如果 △<0,则(41)式可表示为

λ1,2=Re(λ)±iIm(λ),

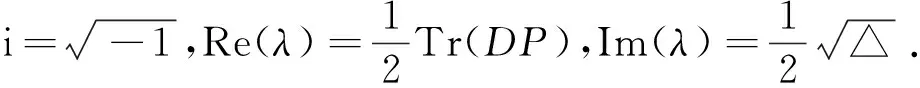
进而可以由特征值的符号及大小判断该周期运动的局部稳定性,具体结果为

情形一: 若特征值的模均小于1,即 |λi|<1(i=1,2),则存在一个稳定的周期运动;

情形二: 若至少一个特征值的模大于1,即 |λi|<1(i∈{1,2}),则该周期运动不稳定;

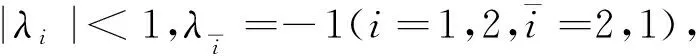
情形五: 若特征值为一对共轭复数,且模为1,即 |λi|=1(i=1,2),则该周期运动存在Neimark分支;

情形六: 若其中一个特征值为0,即λi=0(i∈{1,2}),则该情形为退化情形.

因此, 如果周期运动与不连续的奇异性无关, 那么就可以利用传统的特征值分析来确定周期运动的稳定性.

注2在定理5的证明中,可通过计算求出单位周期内具体的切换时刻及其区间参数,采用同样的方法可以求得另一个周期内的切换时刻区间参数,若两组参数一致,则该系统为具等时切换的不连续动力系统, 可进一步研究其周期-l流; 若l→, 相应系统成为混沌系统,亦可进一步研究其混沌流[3].

本节针对上述两类不连续动力系统,分别在具时间切换的不连续动力系统的切换时刻处,以及具边界转换的不连续动力系统的不连续边界上,定义了转换集及转换集间的基本映射,介绍了不连续动力系统的离散映射动力学的基本理论; 最后采用不连续动力系统的映射动力学方法研究系统的周期运动, 借助系统周期流的一般映射结构以及映射的Jacobi矩阵和特征值, 给出了周期流的局部稳定性和分支预测的解析结果.

4 动态域上不连续动力系统研究进展

应用动态域上不连续动力系统理论可以较为有效地解决不连续动力系统因自身“动态域”与“不连续”所带来的困难.该理论为不连续动力系统动力学研究提供了新的有效方法.近年已相继出现一些运用动态域上不连续动力系统理论进行有效探索的研究工作.

4.1动态域上不连续动力系统若干问题研究

1) 高速旋转齿轮啮合噪声问题研究.这类问题历史上大都是按固定域来考虑，并借助传统连续动力系统的思想方法来研究的；所得结果往往适于近似描述低速齿轮箱的动力学行为.而当高速旋转时，齿轮传递中的振动和噪音变得非常严重，此时用传统方法难以有效揭示高速齿轮传递中产生振动和噪音的机理.2007年Luo和O Connor[40,41]首次运用动态域上不连续动力系统理论研究了这一问题.齿轮传动系统力学模型可以描述为一个周期外力作用下的振子位于另一个振子的两个齿之间.由于两个振子在时变边界上发生相互作用，因而其运动区域是随时间变化的，从而可分为三个运动区域：自由运动区域，此时两个齿轮之间没有相互作用，即两振子自由运动；从动轮左端发生的啮合运动区；从动轮右端发生的啮合运动区.应用映射动力学对上述3类时变区域及相应边界构造基本映射，再通过基本映射的复合可得相应映射结构，从而可对啮合碰撞周期运动和非啮合碰撞周期运动进行解析预测，并可以进行相应稳定性和分叉分析.进一步还可以对混沌运动进行数值模拟，能够模拟得到第一个振子和第二个振子的Poincare映射转换点.转换点描述了两个振子相互接触时的位移和速度，形成了混沌运动的奇怪吸引子.由此可见，对于齿轮箱两个振子碰撞与啮合的动力学问题，运用动态域上不连续动力系统理论能够有效分析其动力学机理，并能将其如此复杂、丰富而又饶有趣味的动力学现象揭示出来.

2) 同步问题研究. 2009年Luo A C J[42]将动态域上不连续动力系统理论用于“同步”的研究，得到了“弹簧”振动系统与“单摆”振动系统同步的充分必要条件.而按传统方法考虑，这两类系统似乎毫不相关，是难以同步.2014年Sun Xiaohui和Fu Xilin[43]研究了弹簧振子模型与VdP振子模型的同步问题；运用流转换理论建立了判断其同步开始出现和同步消失的切换条件,并给出了其出现同步的解析条件.另外，不同于渐近性质下的同步, 此理论可研究有限时间内系统的完全同步和部分时间同步, 并建立转换条件.

3) 碰撞振子模型研究.源于大量机械工程实际连接问题的水平碰撞振子模型，可以从不连续动力系统的角度将其刻划为具体的具边界转换的不连续动力系统[37].如果考虑振子m与底座M水平槽底面的摩擦，该摩擦受制于振子与底座之间的相对速度，而碰撞可瞬时改变振子的速度，因而制约该模型动态域的因素更加复杂.此时其边界可分为两类：一类是速度边界，对应于振子与底座的水平摩擦；另一类是位移边界，对应于振子对底座间隙左右壁的垂直碰撞.对此具摩擦的水平碰撞振子的最新研究[37]表明，系统会发生两种粘合运动：第一类粘合运动，是指振子在间隙内运动时受到的摩擦力太大，振子不能克服摩擦力从而与底座一起运动；第二类粘合运动，是指振子和以底座一样的速度到达间隙左右壁，并意图穿越间隙左右壁，由此振子与底座一起运动.由文献[37]可以看到这类摩擦碰撞振子蕴含着引人入胜的复杂动力学现象.2015年Fu Xilin和Zhang Yanyan[44]运用流转换理论给出了在周期振动下倾斜碰撞振子模型粘合运动和擦边流的动力学新结果.2017年Zhang Yanyan和Fu Xilin[45]研究了具有干摩擦的水平碰撞振子模型的动力学行为；运用不连续动力系统的理论得到了该模型分别在位移边界、速度边界发生的两类粘合运动及擦边流的复杂动力学结果.最近Zhang Yanyan和Fu Xilin[46]还得到了关于倾斜碰撞振子模型周期运动、周期倍分支及稳定性的动力学结果.

4) 脉冲VdP振子模型研究.2014年Fu Xilin和Zheng Shasha[47]从VdP振子方程所描述的LC振荡电路问题出发,具体给出了脉冲VdP系统的构建过程；并运用不连续动力系统的理论得到了该模型关于Chatter动力学新结果.2015年Zheng Shasha和 Fu Xilin[48]运用不连续动力系统的映射理论,对脉冲VdP系统周期运动的动力学行为进行分析和预测,并借助特征值理论得到其局部稳定性准则. 1907年Taylor[49]曾研究金属切削刀具震颤问题.2014年Fu Xilin和Zheng Shasha[50]将该问题的数学模型归结为一类具体的具任意时刻脉冲的脉冲VdP系统，运用动态域上不连续动力系统理论得到了关于这类脉冲VdP系统Chatter动力学的新结果，进而给出了关于金属切削刀具震颤发生与消失的新的判别准则.最近Fu Xilin和Zheng Shasha[51]还得到了关于由VdP振子激励的Fermi加速模型加速性态的动力学结果.

5) 具非对称阻尼性质的不连续动力系统研究. 2018年Sun Guanghui和Fu Xilin[52]利用不连续动力系统理论研究了以悬架系统为实际背景的具有非对称阻尼性质的不连续动力系统的复杂动力学行为.上述工作的特点是所考虑的不连续动力系统模型都是在动态域上来考虑的，都运用了“G函数”作为测度来“度量”不连续边界的奇异性，并运用流转换理论具体分析了边界上流的转换性；有些工作还运用映射动力学理论在“动态域”与“不连续”情形下研究了相应模型的周期运动.

4.2动态域上不连续动力系统研究展望

1) 动态域上不连续动力系统理论仅是初步建立，尚需不断发展与完善[53-57].一方面，针对不连续动力系统“动态域”与“不连续”等自身特征来揭示不连续动力系统本质规律的研究尚需进一步深入.另一方面，对于各类典型的不连续动力系统的研究亟待开拓新路径.譬如切换动力系统：切换动力系统属典型的不连续动力系统.目前从不连续动力系统的角度对切换动力系统的研究还很初步，且主要集中于具时间切换的切换动力系统；而关于具状态切换的切换动力系统的研究工作尚很少见.因此运用不连续动力系统理论发展切换动力系统的理论是十分必要的.又如脉冲微分系统: 脉冲微分系统也属于典型的不连续动力系统.目前关于脉冲微分系统的研究主要集中于具固定时刻脉冲的脉冲微分系统,且主要沿用研究连续动力系统的思想方法来研究.因此从不连续动力系统的角度，运用动态域上不连续动力系统理论来研究脉冲微分系统，是发展脉冲微分系统理论的有效途径.

2) 现代工程与科学技术诸领域中可以用不连续动力系统来描述的实际问题大量涌现，亟待解决[58-61].现代最新研究成果表明，不连续动力系统来源于实践、应用于实践，在机械工程、自动控制、航天技术、机密通讯、生命科学、金融工程、复杂网咯、人工智能等诸多领域都有着广阔的应用前景.在当今大数据、互联网时代，及即将到来的人工智能+时代，呈现并将不断呈现出“海量喷涌的数据量、层出不穷的模型规模、与日俱增的复杂度、日益苛求的精度要求”的态势.伴随着更强大的计算机、更大的数据集和能够训练更深网络的新技术、新方法的出现，对当今时代的实际问题从动力系统角度建模、研究成为可能.而不连续动力系统的自身特征及其研究的思想方法更侧重于从“动态”和“相互作用”角度来思考问题，因而以不连续动力系统作为某些当代实际问题的数学模型可能实现更加有效的近似；换言之，可能实现更有效地描述、分析和预测.

5 结 论

19世纪80年代Poincare建立的连续动力系统的几何理论有两个特点：一是从几何角度来看，其整体拓扑结构直观.这里不必去寻求动力系统的精确解或近似解，而是另辟蹊径，致力于给出在相空间中轨线分布的拓扑结构.二是从分析角度来看，其局部度量精细.通过引入“无切线段”、“轨线上的极限点与极限集”以及“Poincare映射”等作为度量工具，可以将极限分析的思想方法得以有效应用，从而使得精细分析轨线的拓扑结构成为可能.Poincare动力系统的几何理论是展现“数学的哲学魅力”的典范.

本文谈及的“动态域上不连续动力系统理论”也有类似的两个特点.其一是几何直观.动态域上不连续动力系统理论侧重于讨论相空间中动态域不同向量场各类流的分布、穿越与趋势，而避免了寻求对各相关子系统流的精确或近似的繁杂表达.其二是度量精细.G函数实质上是借助极限工具在动边界任一点局部给出一种度量：由G函数的符号来度量动边界任一点附近域流的方向向量与该点法线向量的夹角，进而可以分析流在边界的走向和趋势.也就是说G函数的引入可以将极限分析方法在动态边界局部得以有效应用，从而使得精细研究动态边界上流的转换成为可能.动态域上不连续动力系统理论也蕴藏着“从整体到局部、从几何直观到极限分析”的深刻辩证内涵.