一维Helmholtz方程的四阶优化紧致差分法

孙煜然 朱启华 吴亭亭

(山东师范大学数学与统计学院，250358，济南)

1 引 言

考虑如下一维Helmholtz方程:

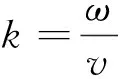
2 Helmholtz方程的优化紧致差分法

本节首先对Helmholtz方程(1)建立带参数的紧致差分格式. 其次, 对其进行收敛性分析和频散分析. 最后,在极小化数值频散的基础上, 提出差分系数的整体选取策略和加细选取策略.

2.1带参数的差分格式的建立本小节建立一维Helmholtz方程(1)带参数的紧致差分格式.

首先, 对区域[0,1]进行N等分,N为一正整数. 空间步长为h:=1/N, 记xm:=mh,m=0,1,2,…,N, 并记Um为u(xm)的差分近似. 其次, 用二阶中心差分Dxxu近似uxx. 由Taylor展开可以得到:

(4)

为建立紧致格式, 需对(4)中的uxxxx进行改写. 为此, 对Helmholtz方程(1)关于x求二阶导数得

uxxxx=fxx-k2uxx.

将上式代入(4), 可以得到uxx的四阶逼近格式如下:

(5)

接下来, 建立零阶项k2u的四阶逼近. 令

(6)

其中c+d=1, 且lh(k2u)是k2u的二阶逼近[8]：

(7)

将(5)式代入(7)式,得到k2u的四阶逼近为

(8)

最后, 联立(5)式和(8)式得到Helmholtz方程(1)的四阶紧致差分格式为

(9)

其中

fm:=f(xm).

类似于文献[8]中定理1的证法, 可得差分方程(9)的解的收敛性分析, 即有如下定理1成立.

定理1假定u是方程(1)-(3)的解, 函数f是足够光滑的, 且kh足够小, 则差分方程(9)的解U存在唯一, 且有如下估计

||U-u||≤Ch4.

上述定理1表明差分格式(9)为四阶格式. 易知, 差分格式(9)为三点差分格式. 因此, 差分格式(9)为带参数的四阶紧致差分格式.

2.2数值波数与真实波数之间的误差分析在本小节中,将分析差分格式(9)的数值波数与真实波数之间的误差. 首先, 通过经典的频散分析得到紧致差分格式(9)的频散方程, 该分析基于波数k为常数和源项f为零的基础上. 为便于分析,将紧致差分格式(9)改写为

As(Um-1+Um+1)+A0Um=B0fm+Bs(fm+1+fm-1),

(10)

其中

接下来, 将Ui:=eikxi代入差分方程(10), 取fi=0, 并利用欧拉公式, 得频散方程:

2AsP+A0=0,

(11)

其中P:=cos(kh). 用数值波数kN替代方程(11)式AS与A0中的k得到关于数值波数与真实波数的方程[4]. 基于该方程,下面定理2给出数值波数kN和真实波数k之间的误差.

定理2对于紧致差分格式(9), 有

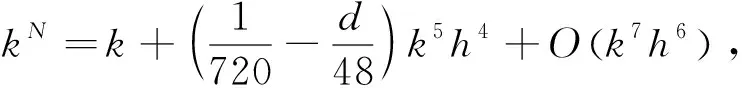
(12)

证令τ:=kh. 又方程(11)中P依赖于τ, 即P(τ)=cos (τ). 定义X：=(kNh)2,由(11)式得

a(τ)X2+b(τ)X+c(τ)=0,

(13)

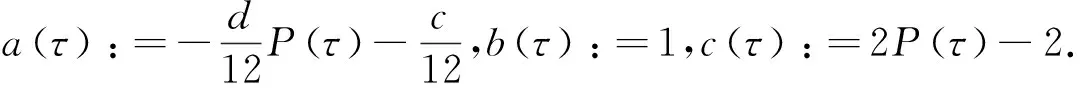
(14)

(15)

由于kN是对k的数值逼近, 故当τ→0时, 应有X→0. 结合方程(13)、(14)和(15),得方程(13)有唯一解

从而, 数值波数kN为

(16)

接下来, 将方程(14)和(15)代入方程(16)得

上述定理表明差分格式(9)的数值波数kN以四阶近似真实波数k. 此外, 与k5h4有关的项称为污染项, 它依赖于波数k和差分格式(9)中的参数.

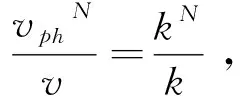
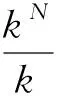
(17)

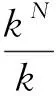
一般的, 可选取IG:=[2.5,400][10]. 下面提出整体的参数选取策略来选择d.

策略1整体的参数选取方法.

在给定的条件IG:=[2.5,400]下, 选取d∈(0,1] 以满足

d=argmin{||J(d,G)||IG,d∈R}.

(18)

下面, 利用奇异值分解法极小化目标函数(18)的方法[9,10]来实施选择策略1.若令

J(d,G)=0,

通过整理得方程

(19)

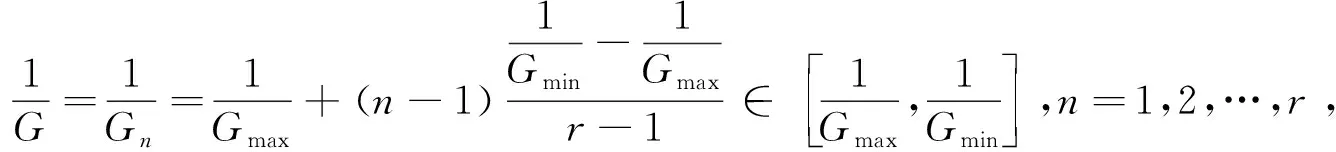
S1d=S2,

(20)

其中

方程组(20)的系数矩阵有r行和1列, 为超定方程组. 选择r=100, 并用奇异值分解法求解方程组(20),可得紧致差分格式(9)的一组优化参数为.

c=0.902 5,d=0.097 5.

(21)

为方便引用, 我们称带有参数(21)的紧致差分格式(9)为一维Helmholtz方程的整体三点差分格式(简称为global 3p).

整体的参数选取方法只给出一组优化参数, 这种做法比较粗糙. 因为对不同的频率和速度等问题,均采用同一组优化参数进行计算,仍可能会产生较大的数值频散. 为进一步提高差分格式的数值精度,下面给出加细的参数选取方法.

策略2加细的参数选取方法.

步骤1：估计区间IG：=[Gmin,Gmax];

步骤2：选取d∈(0,1] 以满足

d=argmin {||J(d,G)||IG,d∈R}.

同样可通过奇异值分解法求解相应的线性系统.

加细的选择方法与整体的相比, 主要区别在于区间IG是根据实际情况变化的. 在表1中列出了多组加细的优化参数. 我们称带加细优化参数(以表1中的参数为加细优化参数)的紧致差分格式(9)为Helmholtz方程的加细三点差分格式(简称为 refined 3p). 另外, 称带有参数c= 1 ,d= 0 的差分格式(9)为Helmholtz方程的紧致三点差分格式(简称为 compact 3p).

表1 加细优化参数

标准化的数值相速度是衡量数值频散的重要标准. 图1给出了compact 3p, global 3p和 refined 3p的标准化的数值相速度曲线. 我们发现 global 3p相比 compact 3p 有较大的改善, refined 3p的数值频散最小. 在数值算例部分将给出更加详细的比较.

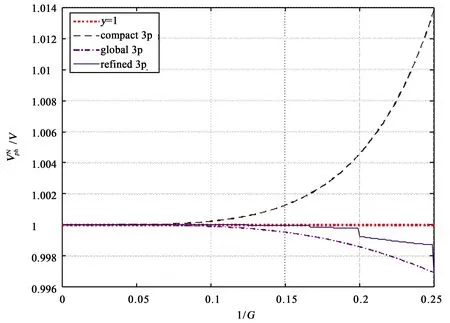
图1 三种差分格式的标准化数值相速度曲线

3 数值算例

在本节,通过两个算例来展示本文构造的差分格式的有效性. 具体地,将比较compact 3p,global 3p,refined 3p这三种差分格式的数值精度. 在计算中，误差范数采用相对C-范数.其中, C-范数具体定义为: 对任意复向量z=[z1,z2,…,zM],其范数为

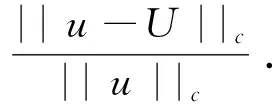
3.1算例1考虑问题(1)-(3), 取f(x)=-1. 此时问题的真解为

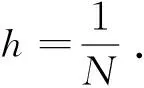
(22)

其中xN+1为虚拟点. 基于方程(1), 有uxxx=-k2ux， 将其代入方程(22), 得到ux的四阶逼近为

综上,得到建立边界条件(3)的四阶近似为

(23)

在计算过程中,把虚拟点xN+1作为未知量处理, 建立个数与未知量个数相同的方程. 为此, 对于节点xm，m=1,2,…,N,应用内部差分格式(9)得到方程, 在虚拟点xN+1处应用(23)式建立方程.

表2、表3为算例1对应于k=200、500时, 不同的网格点数N所对应的三种差分格式的相对C-范数误差. 由表格看出, 当步长相同时, refined 3p 的误差比compact 3p和 global 3p 小得多.在这三种差分格式中, refined 3p的数值精度最高. 对于大波数问题, 为达到相同精度, refined 3p仅需要compact 3p四分之一的节点数.图2、图3进一步说明这三种差分格式均为四阶格式, 与理论分析一致.

表2 算例1,k=200时相对C-范数下的误差

表3 算例1,k=500时相对C-范数下的误差

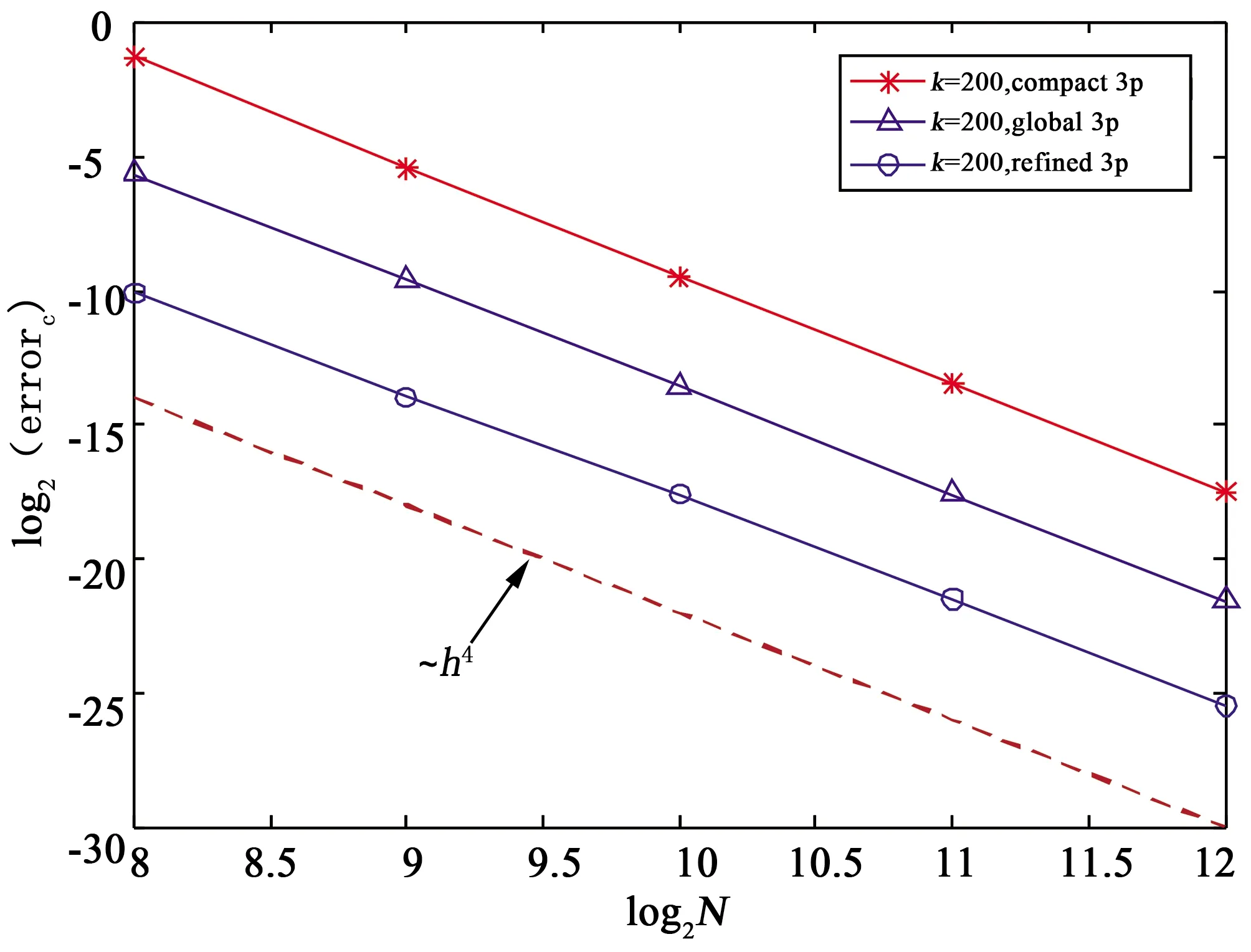
图2 算例1,k=200时相对C-范数下的误差

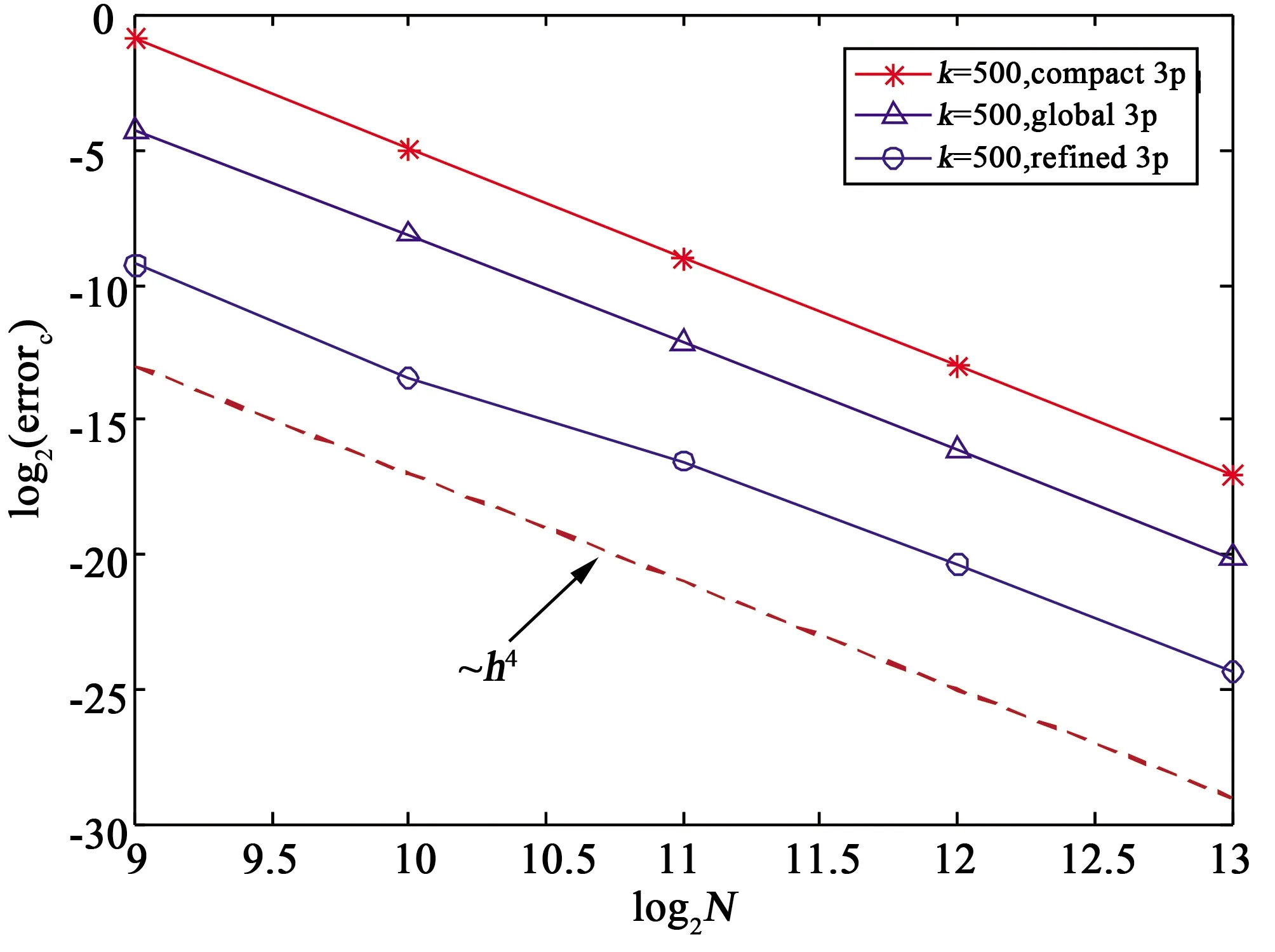
图3 算例1,k=500时相对C-范数下的误差

在图4中,进一步比较了三种差分格式的计算效力. 图4(a),图4(b)分别为算例1对应于三种差分格式在条件kh=1,kh=0.5下的相对C-范数误差.kh为一个常数, 表示每个波长内取的网格节点固定. 在图4中, 波数k由200增加到1 200,我们看到refined 3p的精度始终比compact 3p和 global 3p的精度高. 而且, 随着波数k的增大, compact 3p和 global 3p的误差越来越大, 而refined 3p的误差则维持在稳定的状态, 说明refined 3p可以较好的减弱大波数的污染.

图4(a) 算例1,当k∈[200,1 200]时相对C-范数误差

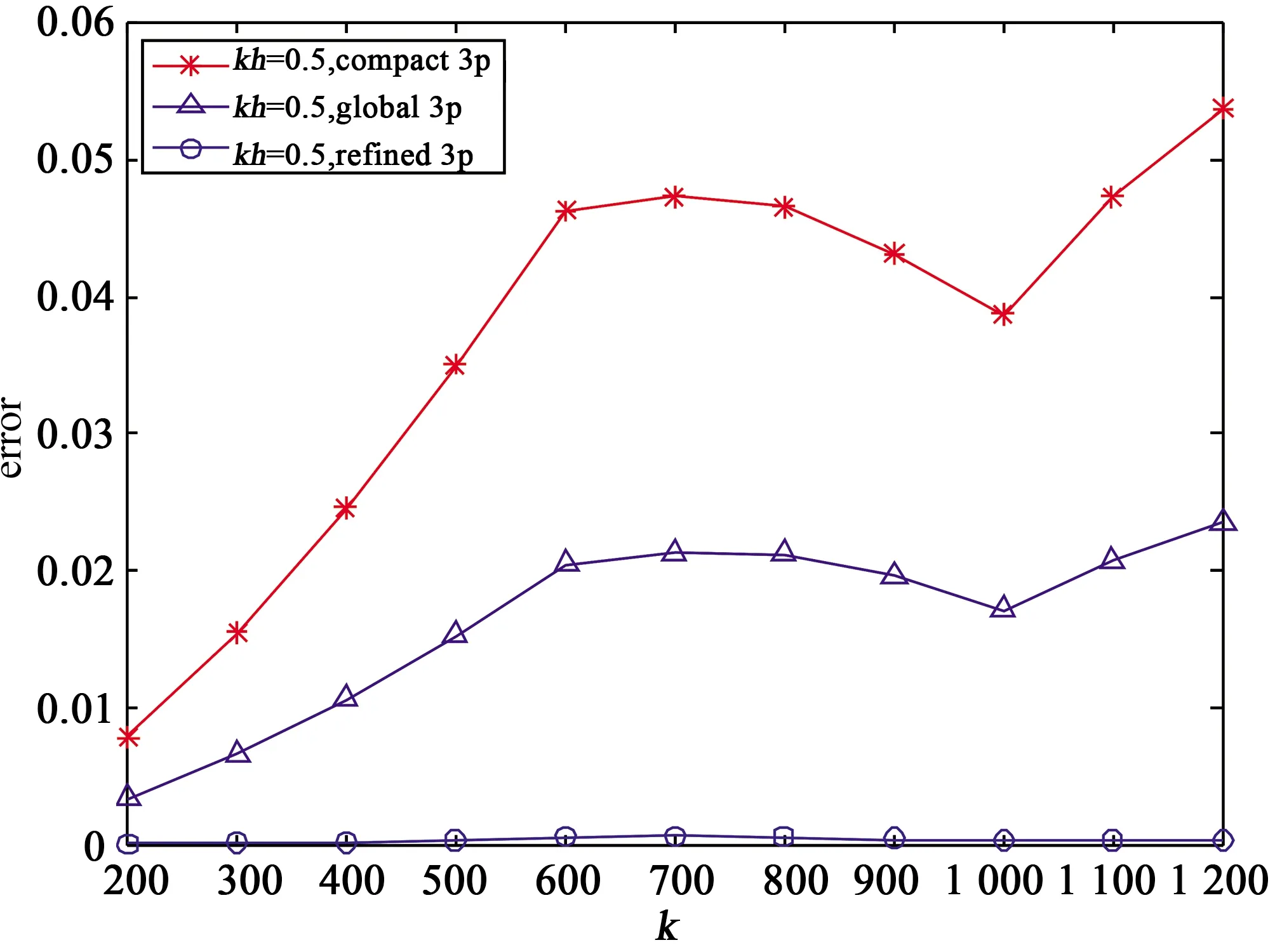
图4(b) 算例1,当k∈[200,1 200]时相对C-范数误差

3.2算例2考虑如下Helmholtz方程：

该问题的精确解为u(x)=eikx. 接下来,用该例子来比较compact 3p, global 3p和refined 3p三种差分格式的数值精度. 在计算中, 边界的处理方式与算例1中对边界的处理方式相同.

在表4与表5中, 给出了对于不同节点数N下k=200、500时的三种差分格式的误差. 容易发现, refined 3p的精度最高. 为达到某一精度, refined 3p仅需要compact 3p一半的节点数即可. 进一步, 图5与图6说明这三种差分格式均为四阶格式, 与理论分析一致.

表4 算例2,k=200时相对C-范数下的误差

表5 算例2,k=500时相对C-范数下的误差

在图7中,对compact 3p, global 3p和refined 3p 这三种差分格式进行了更深入的比较. 图7(a),图7(b)分别给出了三种差分格式在kh=1,kh=0.5时的相对C-范数下的误差. 在这两个图中, 波数k由200增加到1 200, 我们看到refined 3p比其他两种格式的精度要高. 并且, 随着波数k的增大, refined 3p的数值精度的变化相比compact 3p, global 3p的数值精度的变化要缓慢的多, 这说明refined 3p在计算大波数问题时有优势.

综上,compact 3p, global 3p, refined 3p这三种差分格式均为四阶格式. 在这三种格式中, refined 3p的数值精度最高, 并可有效抑制数值频散, 在计算大波数问题时有优势.

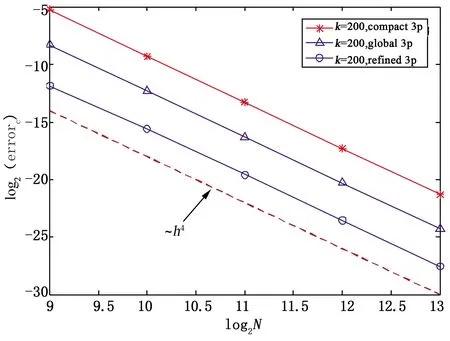
图5 算例2,k=200时相对C-范数下的误差

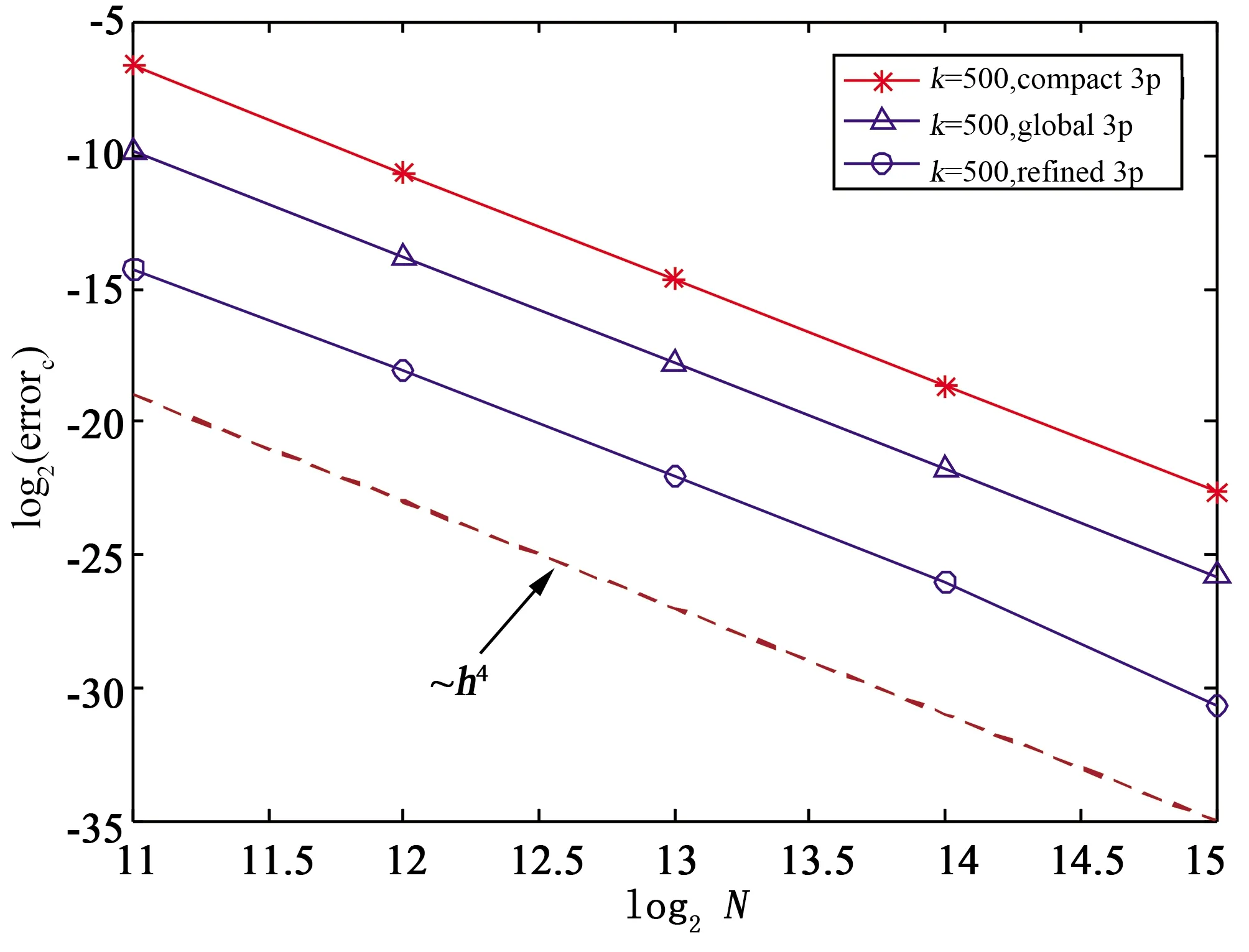
图6 算例2,k=500时相对C-范数下的误差

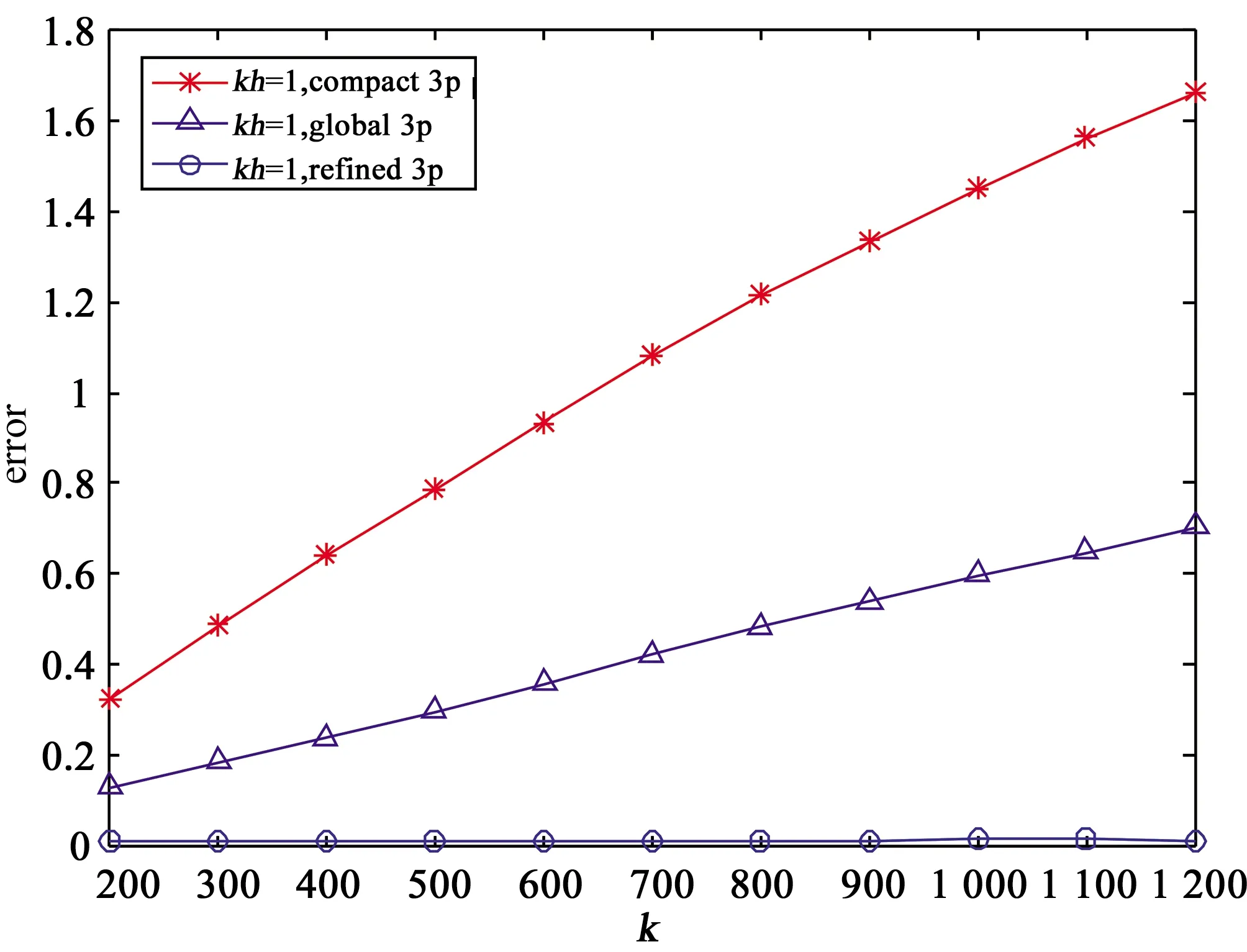
(a)

(b)

图7 算例2,当k∈[200,1 200]时, 相对C-范数误差

4 结 语

本文给出了一维Helmholtz方程的四阶优化紧致差分格式. 首先, 建立了带参数的四阶紧致差分格式并给出收敛性分析. 接下来, 给出了数值波数和真实波数之间的误差分析, 并基于极小化数值频散的思想提出了两种参数选取策略, 同时画出数值相速度曲线, 比较说明加细的参数选取策略效果更好. 最后,通过数值算例验证了所提出的差分格式提高了数值精度,并且有效地抑制了数值频散.