非光滑约束优化的广义增广拉格朗日方法及其在半无限规划中的应用

田冬冬 许雨晴 刘 茜

(山东师范大学数学与统计学院，250358，济南)

1 引 言

考虑非线性约束优化问题：

(P) minf(x)，s.t.gi(x)≤0,i=1,…,m，hj(x)=0,j=m+1,…,l，x∈X,

其中f,gi:Rn→R,i=1,…,m,hj:Rn→R,j=m+1,…l是Lipschitz连续的，X是Rn上的非空闭集.

当所有函数都光滑时，对于问题(P)的二阶惩罚方法是一种非精确的惩罚方法，用来寻找一系列光滑罚问题的稳定点：

当取罚参数c趋于无穷大时，便可以得到原约束问题的稳定点.然而，当罚参数c比较大的时候，罚问题有可能会产生病态，从而解决起来比较困难.增广拉格朗日方法[1]是一种乘子方法，通过对惩罚函数添加拉格朗日乘子的估计构成增广拉格朗日函数, 只需要惩罚参数充分大时，罚问题的稳定点即为原问题的稳定点，从而降低病态产生的可能性.在增广拉格朗日函数的基础上,后来又出现了非线性的增广拉格朗日函数[2]、广义增广拉格朗日函数[3]等, 均为精确的罚函数.

近几年,对于实际问题更多的是要解决非光滑约束优化问题[4-10], 例如在图像恢复、信号重构、最优控制、随机平衡问题及球面逼近等都需要求解非光滑约束优化问题, 而光滑化方法是求解此类问题的一类最常用的方法. 光滑化方法通常会借助光滑化参数ρ→和罚参数c有界, 使之得到原非光滑约束优化问题的最优解.在文献[11]中为寻找对于非光滑非凸约束优化问题的稳定点提出了光滑化增广拉格朗日方法，证明了在罚参数有界的前提下，由算法迭代产生的任何聚点都将是稳定点.文献[10]中所用的增广函数是经典的二次增广拉格朗日函数,是下述广义增广拉格朗日函数的一种特殊情况.

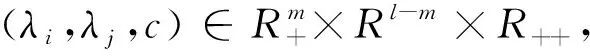
其中

(i1)φ:R→R是严格递增的，在0点处是二阶连续可微的，且

φ(0)=0,φ'(0)=1；

(i2)ψ:R×R→R对b是二阶连续可微的，且有

很容易验证，许多函数满足条件(i1)或者(i2)，例如[10]：

容易知道, 当函数φ=φ1(t)=t, 函数ψ=ψ(a,b)=ab时, 即为文献[10]中给出的增广拉格朗日函数.

2 约束规格

定义1如果存在一个(正)乘子λ∈Rl,使得

定义2[11]若由

可推出

定义3令g:Rn→R是局部Lipschitz函数，已知ρ>0,gρ:Rn→R是一个连续可微函数，如果对于任意固定的x∈Rn，有

则称{gρ:ρ>0}是函数g的一类光滑函数族.

则称光滑函数族{gρ:ρ>0}满足梯度一致性.

定义5已知{xk}为问题(P)的迭代序列，当k→时，ρk→.令为序列{xk}的一个聚点，如果

(1)

(2)

有

λi=0，λj=0,

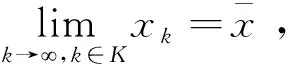
3 光滑化广义增广拉格朗日方法

在本节中, 提出一种光滑化广义增广拉格朗日算法,并运用相关理论证明它的收敛性.

对于光滑参数ρ>0,用广义增广拉格朗日函数定义下面的光滑化广义增广拉格朗日函数：

对于每一个ρ>0,c>0,λ∈Rl,提出下述相应罚问题：

在算法中, 定义下面的剩余函数

剩余函数主要是用来检测不可行性和互补性.

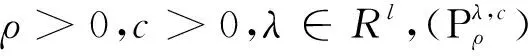
下面将会给出一些相关的理论及其证明. 当ρ→和罚参数c是有界时, 算法产生的任何迭代点的序列都将收敛于问题(P)的一些稳定点. 另外, 定义5给出的拓展的弱无非零反常乘子约束规格保证了罚参数的有界性.

根据定义4给出的精确罚函数，对非光滑约束优化问题提出下列光滑化广义增广拉格朗日算法.

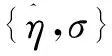
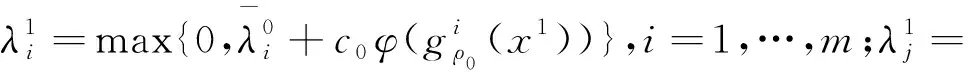
第二步：计算dk=-令xk+1=xk+αkdk，其中αk=βlk,lk∈{0,1,2,…}是满足下面不等式的最小数：

(3)

如果

||

(4)

令ρk+1=σρk，并运行第三步；否则，令k=k+1，重复运行第二步.

第三步：令

(5)

(6)

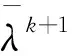
第四步：如果

(7)

返回第一步；否则，令ck=σk+1+ck,k=k+1，并返回第二步.

接下来需要证明算法的收敛性并给出相关的定理, 在此之前先引入下列引理1.

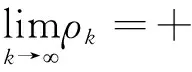
类似于文献[11]中的引理，证明容易得到.

定理1假设算法1 不能在有限步终止, 令x*是序列{xk}的聚点,{xk}是由算法1 产生的.如果{ck}有界, 则x*为问题(P)的稳定点.

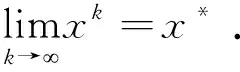
(8)

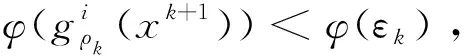
令

计算可得

(9)

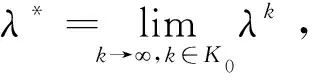
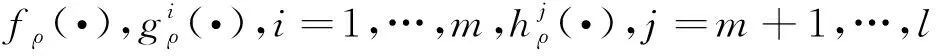
由引理1和(4)式，有

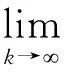
当k→,时，对(9)式取极限，由梯度一致性有

(10)

对于某些i∈{1,…,m}，gi(x*)=0，则有φ'(gi(x*))=1，对(10)式进行简单整理可得

(11)

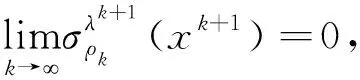
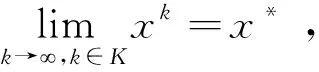
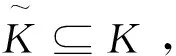
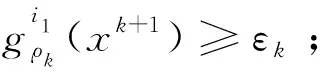
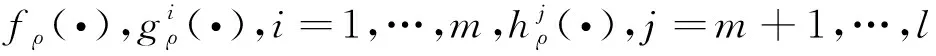
由ck的迭代规则，当k→时，有ckεk→+.因此由的定义以及ψ:R×R→R对b是二阶连续可微的, 而且条件(a)和(b)至少有一个成立,所以有.那么会存在序列和非零μ∈Rl,使得

(12)

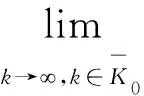
(13)

从定理1中可得出, 对于某些i∈{1,…,m}，gi(x*)≠0，有μi=0；对于剩余的i∈{1,…,m}，gi(x*)=0，则有φ'(gi(x*))=1，对(13)式进行简单整理可得

(14)

下面证明

(15)

条件(14)和(15)与假设的拓展的弱无非零反常乘子约束规格成立是相矛盾的.

下面证μjhj(x*)≥0.因为当k→时，有ck→，所以对于充分大的有

因此

从定理1和定理2可得出下面的推论1.

推论1假设算法1不能在有限步终止,{xk}是由算法1产生的,如果拓展的弱无非零反常乘子约束规格在序列{xk}的任意一个聚点成立，则任一聚点都是问题(P)的稳定点.

4 求解半无限规划问题的光滑化广义增广拉格朗日方法

在本节中,将应用算法1求解半无限规划问题, 问题的形式如下:

minf(x),

s.t.g(x,y)≤0,y∈Ω,

其中，x∈Rn是一个决策变量, Ω是R中一个紧致区间,f:Rn→R是关于x连续可微的函数，g:Rn×Ω是连续可微的.

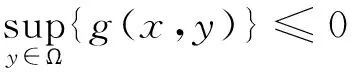
minf(x),s.t.V(x)≤0.

因为值函数V(x)一般为非光滑函数, 在文献[13]中提出了下述积分熵函数来近似值函数V(x)：

当z→x,ρ→+时，γρ(z)→V(x)，在文献[13]中已经给出了积分熵函数是值函数的光滑化函数以及其具有梯度一致性的相关证明.

对于任意给的ρ>0,c>0,λ∈R,定义广义近似光滑化增广拉格朗日函数

通过增广拉格朗日算法1以及引理1、定理1和定理2,可以得到下面的收敛性定理3和定理4.

定理3假设算法1 不能在有限步终止, 令x*是序列{xk}的聚点,{xk}是由算法1 产生的.如果{ck}有界, 则x*为上述半无限规划问题的稳定点.

定理4假设算法1不能在有限步终止, {xk}是由算法1产生的,如果拓展的弱无非零反常乘子约束规格在序列{xk}的任意一个聚点成立， 则任一聚点都是上述半无限规划问题的稳定点.

5 数值实验

在本节中, 主要是通过两个一般的非光滑约束问题来验证光滑化广义增广拉格朗日方法的有效性，另外将会验证光滑化广义增广拉格朗日方法对半无限规划问题也是适用的.

接下来的实验中, 会用三种罚函数对算法1进行检验从而得到问题的稳定点，其中

而对于半无限规划问题, 则采用的是利用积分熵函数法进行光滑化.

算例1[18]非光滑约束优化问题为: 目标函数为最小化非光滑Rosenbrock 函数以及约束函数为一个非光滑不等式约束与一个线性的等式约束，

下面开始对目标函数及约束函数进行光滑化：

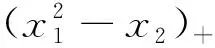
在算例1的数值实验中,选择的初始点为(x1,x2)=(0.3,0.2)，参数

另外ξ=5×10-4，ξ1=10-5.

终止准则为

下述表1中给出的是三种不同罚函数下数值实验结果.

表1 数值实验结果

算例2[20]非光滑约束优化问题为: 目标函数为最小化非光滑Rosenbrock 函数以及约束函数为在变量的加权最大值上的不等式约束为

下面开始对目标函数及约束函数进行光滑化：

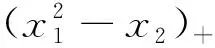
终止准则为

下述表中给出的是三种不同罚函数下数值实验结果.

表2 数值实验结果

上述数值实验可以看出, 满足设定条件的非光滑约束优化问题的稳定点可以通过提出的光滑化增广拉格朗日方法进行求解, 算法产生的迭代序列的聚点便是原问题的稳定点. 由此可验证算法1 是解决非光滑约束优化问题的有效算法.

算例3[21]半无限规划问题为: 目标函数为最小化光滑函数以及约束函数为非光滑的不等式约束，

minf(x)=1.21exp(x1)+exp(x2)，

s.t.g(x,s)=s-exp(x1+x2)≤0,s∈[0,1]，

将目标函数用值函数V(x)=max{g(x,s)}≤0代替，并利用积分熵函数γρ(x)对其进行光滑化，因为积分熵函数是值函数的光滑化函数以及其具有梯度一致性, 从而得到光滑化函数

在算例3的数值实验中,选择的初始点为(x1,x2)=(-1,1)，参数

另外ξ=10-5，ξ1=10-6.

终止准则为

下述表中给出的是三种不同罚函数下数值实验结果.

表3 数值实验结果

上述数值实验可以看出, 满足设定条件的半无限约束规划问题的稳定点可以通过提出的光滑化增广拉格朗日方法进行求解, 算法产生的迭代序列的聚点便是原半无限规划问题的稳定点. 由此可验证算法1 也可以解决半无限规划问题.