分布阶最优控制问题的Petrov-Galerkin谱方法数值模拟

宋家斌 周兆杰

(山东师范大学数学与统计学院,250358,济南)

1 引 言

设Λ=(-1,1),考虑如下控制问题：

(1)

(2)

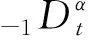
分数阶最优控制问题广泛应用于地下水污染等实际工程问题中. 随着分数阶微分方程数值方法和算法的发展[1-5], 分数阶最优控制问题的数值方法的研究引起众多学者的广泛关注， 例如有限元方法[6,7]、配置法[8]以及谱伽辽金法[9]等. 然而, 据我们所知, 关于分布阶分数阶微分方程最优控制问题数值方法的文献很少. 在文献[9]中,建立了分布阶最优控制问题的谱配置法. 在文献[10]中,采用雅可比-高斯-勒贝格积分公式建立了分布阶最优控制问题的伪谱方法.

本文旨在建立求解分布阶微分方程最优控制问题的Petrov-Galerkin(PG)离散化格式, 利用第一类广义雅可比多项式逼近状态变量, 第二类广义雅可比多项式逼近伴随变量,采用先最优后离散的策略构造了PG谱方法离散格式. 在第二节, 给出了一些必要的微分学预备知识；第三节中,推导了最优控制问题的PG格式；最后,通过数值算例说明了该算法的有效性.

2 预备知识

在这一部分,首先回顾分数阶微积分的有关概念.设n=「α⎤, 这里「α⎤表示大于或等于α的最小整数.

引理1[11]对任意的α∈(0,1], 如果f∈H1(Λ), 使得y(-1)=0并且v∈Hα/2(Λ), 则有

下面引入分布阶索布列夫空间以及广义雅可比多项式. 设Hφ(R)表示在R上的分布阶索布列夫空间, 其范数定义为[5]：

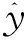
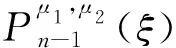
引理2[5]假设α,μ>0且i=1,2, 则有

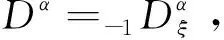
3 Petrov-Galerkin 近似

在这一部分中,将通过先最优后离散的策略建立最优控制问题(1)的PG方法.

3.1离散格式设试探函数空间和检验函数空间分别为

U={v|v∈Hφ(Λ),v(-1)=0},V={w|w∈Hφ(Λ),w(1)=0},

并满足

根据文献[5], 可知双线性形式a(p,q)满足inf-sup条件, 再由引理1, 最优控制问题(1)和(2)的弱形式可改写为

(3)

并且满足下面的等式：

a(y,v)=(f(t)+u(t),v),∀v∈V.

(4)

为了推导连续的一阶最优性条件,定义拉格朗日泛函为

L(y,z,u):=J(y,u)+(f(t)+u(t),z)-a(y,z),

其中z∈V. 然后分别在(y,z,u)方向对L(y,z,u)求导. 注意到

并且

总结上面的方程,得出连续的一阶最优性条件为

(5)

注意到积分约束条件,(5)式中的不等式可以改写为

(6)

其中|Λ|表示Λ的测度. 另外通过分部积分, 由伴随方程可得

(7)

为了建立PG方法的格式, 引入如下有限维的子空间

这里分别采用第一类和第二类广义雅可比多项式逼近状态变量和伴随变量. 由此得出离散分布阶最优控制问题的PG格式为

(8)

其中g(vN)=(f+uN,vN),l(wN)=(yN-yd,wN). 与连续的情况类似,可知

(9)

3.2数值实现本节考虑在一般区间[0,T]的最优控制问题.将一般区间[0,T]映射到标准的区间[-1,1][5],可得

其中

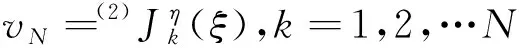
(10)

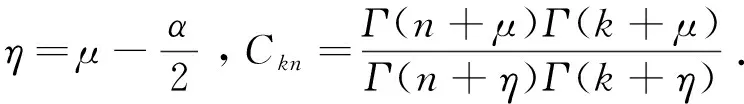
下一步处理α, 从[αmin,αmax]到[-1,1]作映射如下：

然后利用高斯-勒让德求积公式得到

(11)

其中

(12)

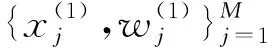
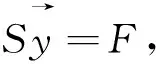
(13)

其中

skn中的积分可以通过下列以(1+ξ)ηj(1-ξ)ηj为权函数的高斯-雅可比-洛巴特数值积分公式求解.

与状态方程一样, 伴随方程类似可得

(14)

其中

根据最优不等式(9),可得

(15)

注意, 这里仍然采用权函数为(1-ξ)μ的高斯-雅可比-洛巴特数值积分公式.

4 数值算例

在这一节中,通过一个数值算例证明PG格式的稳定性.

算例1设问题(1)和(2)中的y,z,u定义如下：

这里T=1,γ=1,α∈(0,1],μ=0.5,φ(α)=Γ(p+1-α)sin(h(α)),右端项f和yd可以通过计算求出.

可以通过选择不同的p值获得光滑解(p=0.5)或不光滑解(p=3).状态变量、伴随变量以及控制变量的精确解与数值解如图1和图2所示.

图1 p=0.5时，y,u,z的数值解与精确解

图2 p=3时，y,u,z的数值解与精确解

表1 p=0.5对应的状态、控制和伴随变量的误差及误差阶

表2 p=3对应的状态、控制和伴随变量的误差及误差阶

当p=0.5或p=3时，状态变量、控制变量以及伴随变量的误差及误差阶分别如表1和表2所示. 可以看出，变量的收敛速度与解的正则性有关，这意味着PG谱方法具有光谱收敛速度.