基于分形理论的水泥制品孔隙特征研究

刘 阳

(1.中赟国际工程有限公司，河南 郑州 450000；2.河南省地质灾害防治工程技术研究中心，河南 郑州 450000；3.郑州市中原智慧地质研究院，河南 郑州 450000)

长期以来，人们对混凝土或水泥制品的研究大多是从耐久性、渗透性、导热性、强度、脆性等方面开展的宏观研究，随着新材料的开发应用和研究手段的升级，科研工作者又开始对混凝土或水泥制品展开一系列的细观或微观研究，揭示其内部孔隙结构的特征以及与力学性能、渗透性能、混凝土或水泥制品导热性能的关系。唐明[1]利用孔隙分形理论对混凝土的孔隙特征进行了分析评价，通过对断面扫描图片的灰度处理，进行了孔隙断面表面分维研究；通过压汞实验堆对孔隙体积分维进行了研究。周胜波[2]针对混凝土细观结构，通过几种分形模型研究对比得出Menger 海绵体模型也适合描述混凝土孔隙特征。刘阳等[3]提出了多孔结构体的孔隙体积分形维数、表面分形维数的算法，在此基础上推导了多孔结构比表面积的计算公式，发现孔隙比表面积与孔隙率和孔隙的表面褶曲粗糙程度有关，孔隙比表面积需要用体积分维和表面分维两个独立变量表示。王学龙等[4]以Menger模型为基础，根据压汞实验计算出多孔镍试件的孔隙体积分形维数为2～3，同时研究了孔径分布与孔隙分形的关系。王清等[5]采用压汞测试方法对土体试样进行孔隙测定，从孔径大于某一孔径的体积累计百分含量的双对数曲线图发现二者的关系图大致分为三段折线，每一段折线代表一个标度不变区间，从而每个折线端点被确定为孔径等级划分的依据。郑瑛[6]和周宏伟[7]基于不同假设研究了多孔结构的分形算法，研究结果却差别很大，说明目前的分形研究计算方法还存在问题。尽管不少学者陆续展开了对混凝土孔隙结构的研究，但是深层次研究的空间依然很大。本文利用孔隙结构分形原理和概率统计规律，系统研究了混凝土孔隙特征与其体积分形的关系，有助于更清晰地认识混凝土的孔隙结构。

1 孔隙体积分形与孔隙率的关系

假设海绵体的孔隙率为φ，则得出φ关于体积分形维数D、边长一次等分数m以及重复挖孔次数k的关系式：

(1)

式中，φk为重复挖孔k次所得到的全部孔隙的累积体积与海绵体的表观体积之比。

由式(1)可以看出，孔隙率与多孔体的体积分形维数呈负相关关系，通过压汞实验得到的体积分维数可以作为评价多孔混凝土结构孔隙率大小的指标。

依据Menger海绵体的构造过程，m=3时，在不同迭代次数下，作孔隙率φ与体积分形维数DV的关系图，如图1和图2所示。

图1 孔隙率-孔隙分形关系

图2 迭代次数k与孔隙率的关系

孔隙率φ是关于体积分形维数DV的减函数(图1和公式(1))。多孔结构的体积分形维数越大，孔隙率越低；迭代次数对孔隙率的影响也很大，迭代次数越高，孔隙率越大。

孔隙率随迭代次数k升高而增大(见图2)。一般来讲，迭代次数越高，能检测到的孔径范围增大，测得的孔隙体的容积就越大，孔隙率就越高，只是小孔径所占的比例太大，孔隙率增长幅度有所限制。同时，四条曲线的斜率有所差别。分形维数越大，φ随k变化的曲线斜率越小；分形维数越小，φ随k变化的曲线斜率越大。压汞实验过程中，迭代次数越高，对应的汞压越大，因此孔隙率随汞压力的变化幅度能反映多孔结构的孔隙结构分形情况。

2 孔隙体积分形与孔径分布的关系

混凝土多孔体系中，孔径的分布范围为(rmin，rmax)，假定孔径随机连续分布，孔径分布满足标度不变性，具有明显的分形特征[8]。根据分形几何原理和孔径分布的随机性，设定F(r)为孔径不大于r的孔隙分布函数，其函数表达式为：

(2)

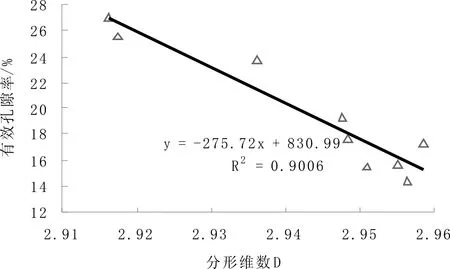
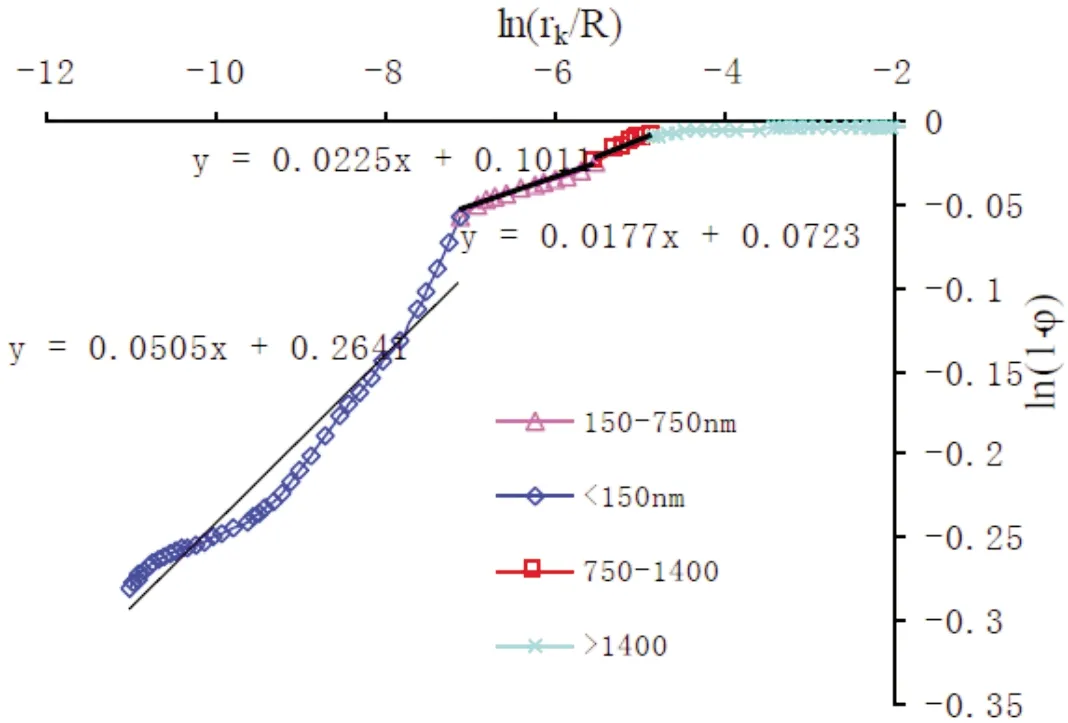
式中，D代表多孔结构体的体积分形维数，2

根据概率密度函数的性质，得出：

(3)

y(r)为孔径概率密度函数，可以用孔隙体积分形维数D表示：

(4)

由式(3)解得：A=-1/(rmin-D-rmax-D)

(5)

将式(5)代入式(3)得到孔径概率密度函数y(r)关于孔隙体积分维D的表达式：

y(r)=1/(rmin-D-rmax-D)·D·r-D-1

(6)

将式(5)代入式(2)得到孔径分布函数F(r)关于孔隙体积分维D的表达式：

(7)

孔隙体积分形D与中值孔径μ的关系可以从概率统计学角度得出中值孔径μ的期望计算公式：

(8)

图3 孔径概率分布密度与孔径的关系

孔径概率分布密度与孔径的关系如图3所示。

由图3可以看出：孔隙概率分布密度y(r)与孔径r的双对数曲线呈线性关系，符合分形特征，对该双对数曲线的斜率取绝对值就得到孔隙分形维数D；孔隙分维数越大，孔径概率分布密度越小，孔径的分布区间越宽。因此，可以用孔隙体积分维数D来表征孔径分布的均匀程度。

孔径分布函数与孔径的关系如图4所示。

由图4可以看出：78%～85%的孔径分布在1.0×10-7～2.0×10-7，小孔数量占的比重非常大，但由于小孔容积过小，对混凝土多孔结构的孔隙率的影响程度可能并不大。沿纵坐标轴85%的位置作一条水平线与四条孔径分布函数曲线相交，找出对应的孔径值，发现体积分形较大的样品对应的孔径值较小，体积分形较小的样品对应的孔径值较大。这说明孔径在分布区间上的概率与多孔体的体积分形有关。

中值孔径与体积分形的关系如图5所示。

由图5可以看出：孔径的中值孔径与多孔体的体积分形有关，随着混凝土多孔结构的体积分形维数变大，孔隙体的中值孔径趋于减小。这一结论很好印证了孔径分布函数-孔径关系。

图4 孔径分布函数与孔径的关系

图5 中值孔径μ与体积分形维数D的关系

3 硬化水泥浆体压汞实验

为了验证以上理论公式的适用性，按照掺合料、水灰比、减水剂等不同比例制备9组样品，标准养护28 d后进行压汞实验，结果见表1，绘制相关曲线，如图6、图7所示。

表1 水泥石孔径分布情况

图6 水泥石孔隙率与分形维数的关系

图7 水泥石平均孔径与分形维数的关系

由图6、图7可知：水泥石的孔隙率随孔隙分形的增大成直线减小；水泥石平均孔径随着分形维数的增大也不断下降，大致呈直线关系。实验结果与本文推导的式(8)和图4、图5的分析结论相吻合。

对9#水泥制品试件压汞实验分析，结果如图8、图9所示。

图8 9#试件ln(1-φ)与ln(rk/R)关系曲线

图9 9#水泥石孔径的概率分布密度

由图8、图9可知：9#水泥石的孔隙结构大致分为2个明显的分形区间，孔径大于150 nm的孔隙分形维数为2.977～2.982，孔径为10～150 nm的孔隙分形维数为2.950。大孔径区间的分形维数大，其概率分布密度就低，所以图9的右边峰值就低，但是其分布区间较宽，孔径范围达300～2 000 nm；小孔径区间的分形维数小，其概率分布密度就大，所以图9的左边峰值就高，但是其分布区间较窄，孔径范围为10～200 nm。实验结果与本文推导的式(6)和图3分析结论相吻合。

4 结论

(1)水泥制品的孔隙率可以用体积分形这一标度不变量表示。水泥制品的体积分形维数越大，其孔隙率就越低，二者呈负相关关系。

(2)孔隙率随汞压力的变化幅度能反映多孔结构的孔隙结构分形情况，孔隙率随迭代次数k升高而趋于缓慢增长；不同的分形维数下，孔隙率随迭代次数变化的幅度有所差别。

(3)孔隙体积分维数D能用来表征孔径分布的均匀程度。孔隙分维数越大，孔径概率分布密度越小，孔径的分布区间越宽。

(4)中值孔径与孔隙率呈正相关，中值孔径随水泥制品的体积分形维数的增大而趋于减小，这与孔隙率与体积分形的关系相一致。用分形维数来评价水泥制品的孔隙结构特征是可行的，但仍需进一步研究。