大跨简支钢箱梁桥荷载试验研究
曾 勇,曾渝茼,范和平,罗小清,张亭亭
(1.重庆交通大学 省部共建山区桥梁与隧道工程国家重点实验室,重庆 400074;2.重庆交通大学 山区桥梁结构与材料教育部工程研究中心,重庆 400074;3.忠县畅达建设投资有限公司,重庆 404100;4.山东广信工程试验检测集团有限公司,山东 济南 250002)
我国交通运输行业持续蓬勃发展,大跨简支钢箱梁桥的数量逐渐增多。为了保证此类桥梁设计的可靠性和施工质量,其承载能力需要进行评估。荷载试验因其便捷、可靠的优点被业界广泛运用。马超等[2]提出了评述桥梁荷载试验的主要步骤及要点,表明桥梁荷载实验主要是通过模拟实际运营时的最不利荷载情况,然后经过实测值与计算值对比分析而达到评定桥梁结构是否可靠的效果;贾毅等[3]对简支组合梁桥进行了荷载试验研究,并验证了其结构可靠性;梁宁一等[5]对轨道专用桥展开了荷载试验研究,并对其进行控制计算分析;李元兵等[6]对千米级斜拉桥开展了结构静力行为试验研究,验证了其桥梁结构设计的可靠性;李龙等[7]对小边跨梁拱组合体系桥梁进行了静动力荷载试验与结构评定分析;傅光奇等[8]对钢板加固后的简支梁桥开展了荷载试验(静载)研究。目前,国内外对于大跨简支钢箱梁桥荷载试验研究还较少,由于同类桥梁数量较多,因此对大跨简支钢箱梁桥进行荷载试验对同类工程具有一定的参考意义。
本文对某大跨径简支钢箱梁桥开展了静载试验。研究在正载及偏载两种荷载工况下该桥主梁控制截面的应力、应变和挠度值,将荷载试验得到的实测值与有限元软件建模计算的理论值进行对比分析,并且对试验前后控制截面其他异常(如裂缝等)现象进行观测。通过该桥的静载试验研究,综合分析其承载能力、实际运营状况,为同类工程问题提供参考。
1 工程概况
该桥为单跨40 m的单箱单室简支钢箱梁桥,梁高1.8 m,桥梁宽度为7.5 m;横断面布置:净6.5 m+2×0.5 m,防撞护栏,双向两车道;桥台为U 型桥台+扩大基础;支座为盆式橡胶支座。设计荷载标准为:公路-I级。钢箱梁桥总体布置图见图1。
为了测试某大跨简支钢箱梁桥的承载能力是否达到要求,验证桥梁设计是否可靠和施工质量是否达标,在桥梁修建完成后例行荷载试验。主要内容:检测正载及偏载两种荷载工况下该桥主梁控制截面的应力、应变和挠度值,将荷载试验得到的实测值与有限元软件建模计算的理论值进行对比分析。
2 静载试验
2.1 试验方法
(1)挠度检测:共设置5个挠度检测截面。挠度检测使用的仪器是分辨率为±0.01 mm的精密水准仪。

图1 钢箱梁桥总体布置图
(2)应力(应变)检测:共设置1个应力(应变)检测截面。应变检测使用的仪器是分辨率为±1×10-6(1 με)的应变片和静态应变仪,依照材料的弹性模量理论值计算测点的应力值,应变测点均设置在相应检测控制截面的表面上。
(3)裂缝观测:裂缝观测使用的仪器是分辨率为±0.02 mm的裂缝观测仪。
2.2 应力及挠度理论计算
使用桥梁结构分析软件MIDAS/Civil 2019严格按照该桥的设计资料和设计规范进行有限元模型的建立(如图2所示),根据相关桥梁设计规范规定,模拟桥梁实际运营荷载情况以及最不利荷载情况等因素进行计算。计算结果为:最大挠度计算值为42.33 mm,最大应力计算值为66.5 MPa。

图2 有限元计算模型图
2.3 测点布置
2.3.1 静力挠度测点
该桥在纵向共设置5个挠度检测控制截面,测试仪器是分辨率为±0.01mm的精密水准仪,分别在各控制截面两侧的栏杆附近设置测点,该桥挠度测点设置见图3。
2.3.2 静力应变测点
本桥共设置1个应变(应力)检测截面J1,在箱梁下表面设置控制截面应变测点。应变检测使用的仪器是分辨率为±1×10-6(1 με)的应变片和静态应变仪,应力通过实测应变值经过力学计算得来。应变测点设置如图4所示。
2.4 试验荷载及加载位置
2.4.1 试验荷载布置
偏载荷载工况下,加载车辆布置如图5所示,正载荷载工况下,加载车辆布置如图6所示,图中尺寸单位为cm。

说明:“”标记为水准挠度测试截面。
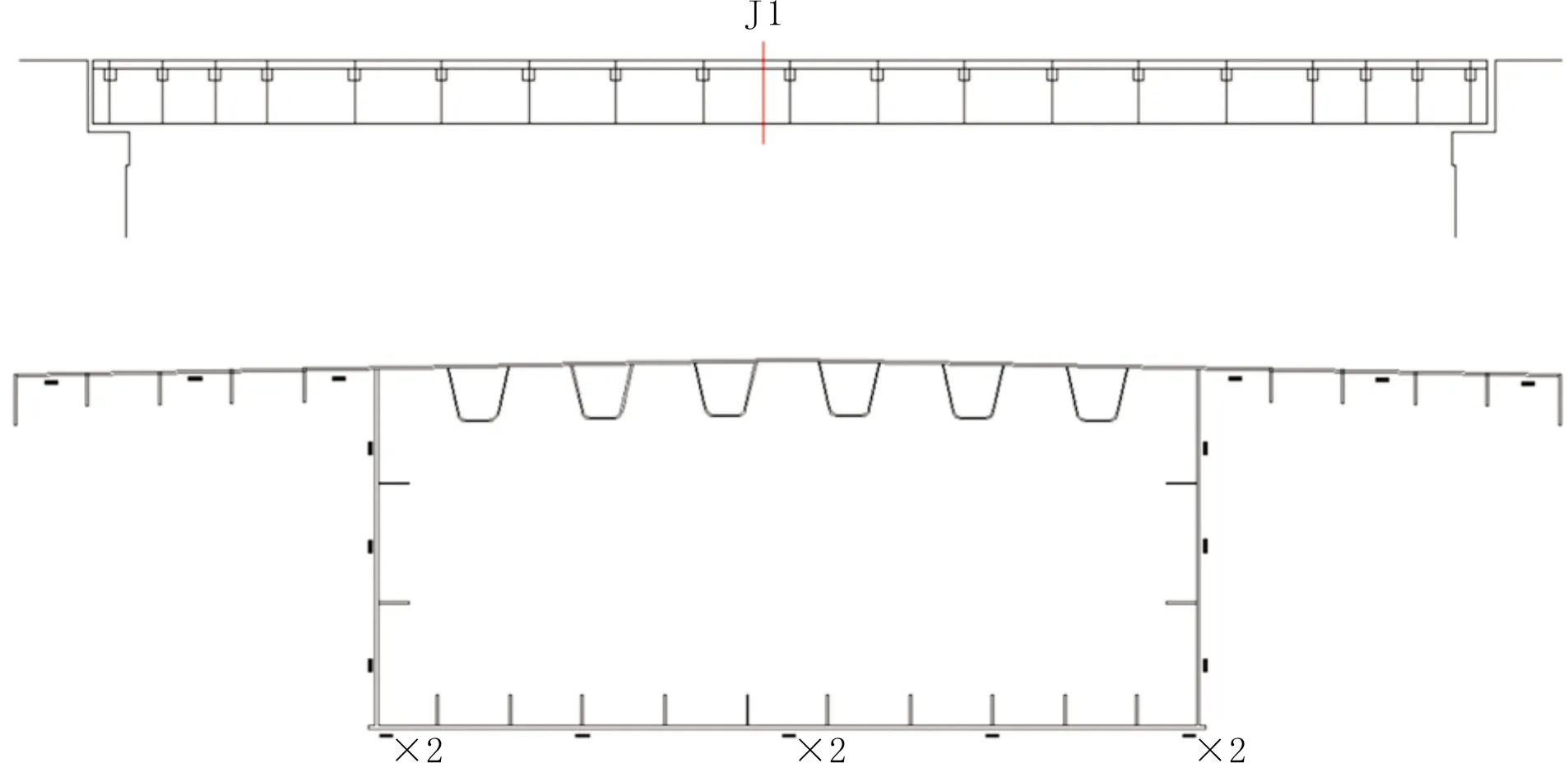
说明:图中“”标记为静应变测点,“x2”表示该部位布置应变测点的数量为2,未标注则仅设置1个应变测点。

图5 J1截面偏载时车辆布置图

图6 J1截面正载时车辆布置图
2.4.2 加载车辆
试验车辆选择三轴车,图7为试验车辆示意图,其中:a=3.85 m,b=1.35 m,轮距1.80 m。

图7 试验车辆示意图
2.5 静载试验效率
运用载重三轴车来模拟静力荷载,荷载试验所需三轴车的重量与数量,根据最不利荷载等效值按式(1)计算:
(1)
式中:η为静力试验荷载效率;Sstate为静载荷载作用下,计算效应值;S为设计控制荷载作用下的最不利计算效应值;μ为冲击系数。对本桥进行的静载试验荷载效率计算结果见表1。

表1 静载试验荷载效率计算表
3 试验结果
3.1 挠度测试结果
按照预先设计的实验方案对该桥进行静力加载试验,挠度检测使用的仪器是分辨率为±0.01 mm的精密水准仪。为直观分析应力测试结果,将基于有限元法的理论计算值与本实验得到的实测值同时绘制。正载和偏载两种工况下,测点挠度的试验实测值和基于有限元法的理论计算值对比分别如图8和图9所示。

图8 J1截面正载挠度测试结果

图9 J1截面偏载挠度测试结果
3.2 应力测试结果
为直观分析应力测试结果,将基于有限元法的理论计算值与荷载试验实测值同时绘制。正载和偏载两种工况下,测点应力的试验实测值和基于有限元法的理论计算值对比分别如图10和图11所示,图中应力符号规定:梁体混凝土受拉为正,受压为负;设置多个测点的测试部位,取平均值。

图10 J1截面正载应力测试结果

图11 J1截面偏载应力测试结果
3.3 裂缝观测结果
加载试验前后,对测试截面附近主梁和铺装层进行裂缝观测,应力测试截面控制区域铺装层未发现可见裂缝,由此可见,该桥的抗裂性设计达到相关规范要求。
3.4 试验结果评定
3.4.1 结构刚度评定
通过试验荷载下结构实测挠度与基于有限元法的理论计算值对比分析来评定结构刚度,为了使试验结果更直观,将相应试验桥跨的主要挠度检测结果汇总列于表2,其中最大弹性变形单位为mm。

表2 挠度测试结果汇总
由表2可知:试验荷载加载后,各控制截面的实际挠度均比理论计算值小,挠度校验系数处于较合理的范围:0.73~0.94。该桥最大实测挠度增量为38.30 mm,约为跨径的1/1 018。正载和偏载两种工况卸载后,控制截面实测相对残余变形最大为17.6%,小于规范值。图8和图9所示的桥跨结构挠曲线走势光滑连续,与基于有限元法的理论计算曲线具有较好的一致性,表明该桥桥跨结构实际运营状态良好。
3.4.2 结构强度评定
通过试验荷载下结构实测应力与基于有限元法的理论计算值对比分析来评定结构强度,为了使试验结果更直观,将全桥应力检测截面的主要检测结果汇总列于表3。

表3 应力测试结果汇总
分析表3的实测应力数据可知:该桥控制截面的实测应力为0.24~0.98,与基于有限元法的理论计算值相比,在正常范围之内,因此该桥结构强度达到要求。
4 结论
(1)各控制截面的实际挠度均比理论计算值小,挠度校验系数处于较合理的范围(0.73~0.94)。该桥最大实测挠度增量为38.30 mm,约为跨径的1/1 018。正载和偏载两种工况卸载后,控制截面实测相对残余变形最大为17.6%,小于规范值。图8和图9所示的桥跨结构挠曲线走势光滑连续,与基于有限元法的理论计算曲线具有较好的一致性,表明该桥桥跨结构实际运营状态良好,结构刚度满足设计要求。
(2)该桥控制截面的实测应力为0.24~0.98,与基于有限元法的理论计算值相比,在正常范围之内。各工况实测应变曲线均位于理论应变曲线下方,且变化趋势基本一致,表明桥跨结构强度与理论计算一致性较好,结构强度满足设计要求。
(3)该桥在98%荷载效率的静力加载试验过程中,未出现任何异常,实测该桥最大残余应变仅为10%,最大残余变形仅为17.6%,表明在整个静力荷载试验过程中该桥一直处于弹性工作状态。
(4)加载前后,箱梁测试截面附近区域内,主梁及铺装层未发现新增的可见横向裂缝。

