盘扣式竖向支架有限元分析

师 政，李树山，张锋剑，李国耀，曹夫利，

(1.华北水利水电大学 土木与交通学院，河南 郑州 450045；2.河南城建学院 土木与交通工程学院，河南 平顶山 467036；3.平煤建工集团有限公司，河南 平顶山 467000)

图1 试验加载图

近年来，随着社会不断地发展，越来越多复杂的超高层建筑被设计建造，其中离不开脚手架的使用。目前，大量学者对不同形式脚手架进行试验研究及有限元模拟分析[1-6]。刘臻洲[7]认为几何缺陷和材料缺陷对管桁架承载力影响重大，并运用概率统计理论及方法建立了该结构的缺陷随机分布和参数统计信息，并进行缺陷状态下有限元模型验证。梁修建[8]认为由于钢管的可重复利用性，材料存在不同程度的初始缺陷(钢管壁厚、立杆初始弯曲等)对支撑架的稳定承载力影响重大，并进行有限元模拟分析验证。

本文基于文献[9]的试验结果，对新型旋转盘扣式支架进行有限元建模，并对有限元模型进行修正，考虑初始偏心及结构刚度对计算结果的影响，并与试验结果对比分析。

1 试验概况

文献[9]对新型旋转盘扣式支架进行足尺试验，研究其极限承载力情况(见图1)，位移测点布置在竖向支架顶层加荷端两侧的节点上，采用10 cm型数字位移计，用以测量竖向支架的位移变化，如图2所示。竖向支架达到极限荷载发生屈曲破坏后其荷载-位移曲线，如图3所示。杆件基本参数见表1。

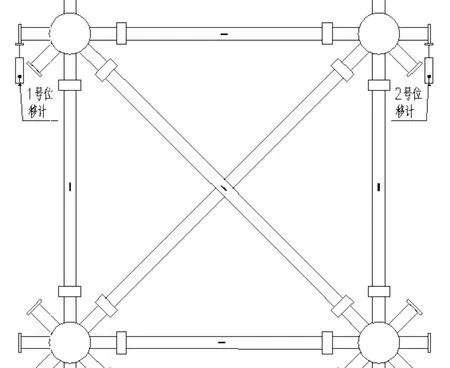
图2 位移计位置图

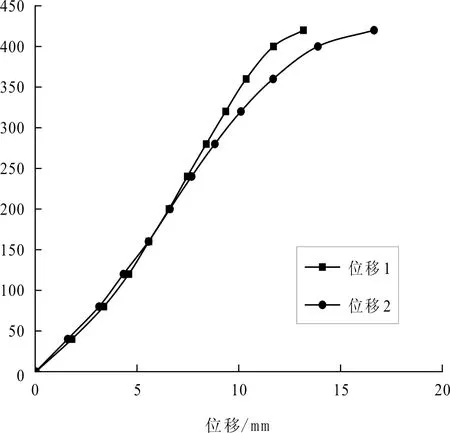
图3 荷载-位移曲线图

由图3可以得出：足尺试验竖向支架的极限承载力为420 kN，结构发生屈曲破坏时顶层节点处的最大位移为15 mm(取两个位移的平均值)。

表1 杆件基本参数

2 有限元模型设计及结果

2.1 单元选择

本文为了简化有限元模型，全部采用管单元PIPE289建模，PIPE289单元具有拉压、弯曲和扭转性能且在每个节点上有六个自由度(X、Y、Z方向三个转动自由度及三个平动自由度)，适用于细长至中粗管结构的分析，且适用于线性分析、弧长法或非线性稳定方法研究倒塌问题。

2.2 计算模型

根据单跨四步竖向支架体系，采用ANSYS有限元分析软件建立基础模型，如图4所示。本次模型采用11比例建模，节点采用刚接方式，底座约束采用刚接方式连接。本文采用等向强化的Mises屈服准则，采用弧长法为收敛准则，有限元模型每个杆件划分为一个单元。对竖向支架顶部4个节点施加竖向荷载，随着荷载的增加，支架结构由弹性阶段逐渐进入塑性屈服阶段直到结构最终丧失承载力计算终止。

图4 三维模型(a)及约束与加载方式(b)

2.3 计算结果

有限元计算结果及荷载-位移曲线，如图5～图7所示。

图5 Y方向位移

图6 竖向支架应力值

图7 荷载-位移曲线

由图5、图6可以看出，竖向支架的极限承载力为645 kN，最大位移为8.10 mm，在第四层竖向杆件处承受应力最大值为336.82 MPa。由图7可知：试验结果与有限元计算结果相差较大，分析得出，由于新型盘扣式竖向支架具有拼接特性，即节点连接处有缝隙存在，极易出现偏心情况，另外，在实际情况中，钢管的壁厚存在偏差，应该对竖向支架考虑初始缺陷建模。

3 模型修正

为提高计算结果的准确性，需对原有限元模型进行修正，即分别对原有限元模型制造受压结构的初始偏心和调整结构刚度。本文考虑对竖向杆件的X轴方向偏移0 mm、1.5 mm、3 mm；对杆件的壁厚调降0%、4%、8%，以探究对有限元模型极限承载力的影响。修正后的有限元模型计算结果如表2所示。

表2 修正后有限元模型计算结果

注：极限位移为极限荷载下的位移值，极限荷载偏差、极限位移偏差均与试验数据比较。

由表2可知，在有限元模型中对竖向杆件X轴方向偏移3 mm，制造受压结构的初始偏心缺陷；通过折减杆件壁厚为原始壁厚的92%来调整结构刚度，有限元计算模型与试验数据相差不大。计算结果如图8～图10所示。

图8 Y方向位移

图9 竖向支架应力值

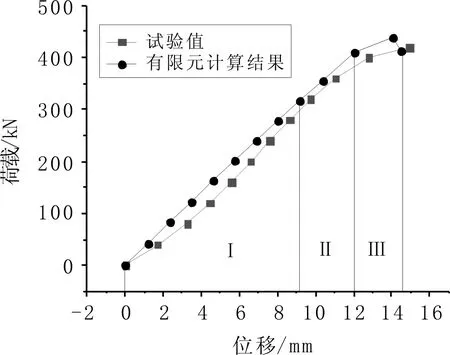
图10 荷载-位移曲线

由图8、图9可以看出：通过建模计算，Y方向上的竖向支架最大位移发生在节点与杆件连接处，为15.13 mm，Y方向上的竖向杆件顶端节点位移为14.09 mm。修正后的有限元模型极限承载力为438 kN，与试验结果基本一致。竖向支架在第三层承受较大的应力，应力值为344.99 MPa。由图10可知：修正后的有限元模型与试验结果破坏过程基本相同，且数值较吻合。破坏过程分为三个阶段：第Ⅰ阶段为线弹性阶段，第Ⅱ阶段为弹塑性阶段，第Ⅲ阶段为屈曲破坏阶段。

4 结论

对新型旋转盘扣式竖向支架进行有限元分析，得到以下结论：

(1)新型旋转盘扣式竖向支架在理想状态下建立的有限元计算模型并不符合实际受力情况，需根据几何缺陷及材料缺陷对有限元模型进行修正。

(2)对竖向杆件X轴方向偏移3 mm，制造初始偏心缺陷，并折减杆件壁厚为原始壁厚的92%来调整结构刚度，其有限元模型能较好地模拟新型旋转盘扣式竖向支架的实际受力情况，有限元计算结果与试验值吻合较好，该模型为以后工程应用和科学研究提供参考。

(3)修正后有限元模型与试验结果的破坏过程基本相同，破坏过程分为三个阶段。