高考数学题解题技巧初探

王继扬

(福建省南安市华侨中学 362333)

高中数学是一门逻辑性和抽象性比较强的学科，在高考中占有很多分数，同时也是其他学科的基础，因此，高中数学的教学是十分重要的.在高考试卷中，数学有三种题型，选择题、填空题和解答题，学生想要取得好成绩，不仅要扎实地掌握数学知识，还要有一定的解题技巧，这样才能够帮助学生更好地发挥，提高解决问题的能力.

一、选择题解题技巧

1.直接法

直接法是指学生综合数学概念、性质、法则、公式和定理直接地将题目解答出来，这种方法需要学生具备扎实的数学基础知识.

例1 (2014全国Ⅰ卷选择题3)设函数f(x)，g(x)的定义域都为R，且f(x)是奇函数，g(x)是偶函数，则下列结论正确的是( ).

A.f(x)g(x)是偶函数 B.|f(x)|g(x)是奇函数

C.f(x)|g(x)|是奇函数 D.|f(x)g(x)|是奇函数

解析假设f(x)为奇函数,g(x)为偶函数.因为奇偶得奇：f(-x)g(-x)=-f(x)g(x)；奇奇得偶：f(-x)f(-x)=f(x)f(x)；偶偶得偶：g(-x)g(-x)=g(x)g(x)；绝对值奇为偶：|f(-x)|=|-f(x)|=|f(x)|；绝对值偶为偶：|g(-x)|=|g(x)|.所以,C是正确的.

2.代入验证法

高考数学选择题中有四个选项，如果学生无法确定到底哪个是正确的，可以将所选的答案代入到原题中进行验证，观察结果是否满足问题中的条件，然后选择符合要求的问题设置的选项.

例2 (2014，全国Ⅱ卷选择题1)设集合M={0,1,2}，N={x|x2-3x+2≤0}，则M∩N=( ).

A.{1} B.{2} C.{0,1} D.{1,2}

解析把M={0,1,2}的数代入不等式x2-3x+2≤0，经验证x=1,2满足.

二、填空题解题技巧

1.数形结合法

数学是一门含有数和图的学科，因此在解题时可以将数和图进行结合，将抽象的数学形象化的展示出来，方便学生思考，并在此基础上解题，作出符合题意的图形，做到数中思形，以形助数，并通过对图形的直观分析、判断，则往往可以简捷地得出正确的结果.

例3 (2014·北京卷填空题11)某三棱锥的三视图如图所示， 则该三棱锥最长棱的棱长为____.

分析此题是一道几何背景明显的高考数学填空题， 可以先还原其几何体求出相关棱长.

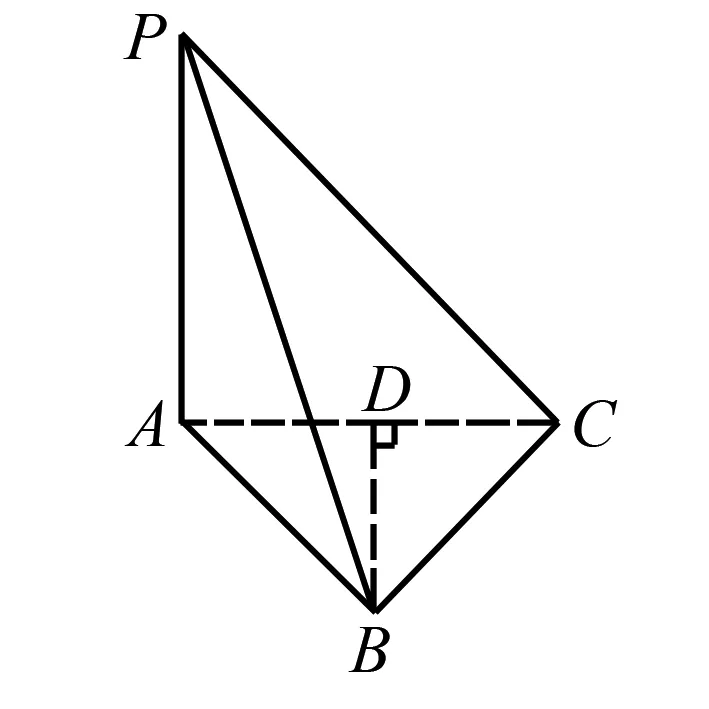
解析根据三视图还原几何体，得如图所示的三棱锥P-ABC.

由三视图的形状特征及数据，可推知PA⊥平面ABC，且PA=2.底面为等腰三角形，AB=BC.

2.等价转换法

学生在解题的过程中如果遇到比较抽象的题，就会很难解答，可以转换一下数学思想，从不同方向思考问题，将不常见的填空题型转换为我们见过的题型，不仅增加了自己对高考数学的信心，也提高了高考数学填空题答案的准确度.

例4 (2014，全国卷Ⅲ填空题14)函数y=cos2x+2sinx的最大值为____.

分析此题就是值域问题，先利用倍角公式将不同名称的三角函数转化为相同名称，再借用参数将原函数转化为我们熟悉的二次函数.

三、解答题解题技巧

1.辨别题目类型

对于高考题中的概率题来说，能够辨析和辨型，针对题目来将其划分种类，然后利用此种类型的公式或思路解题.

例5 (2014江苏高考综合题22)盒中共有9个球，其中4个红球，3个黄球和2个绿球，这些球除颜色外完全相同，从盒中一次随机取出2个球，求取出的2个球颜色相同的概率P.

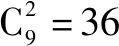
2.根据题目内容建模、建系

在解答解析几何类综合题时，可以根据题型设计出与题目相关的坐标体系，帮助形成立体化的思维图形，进而帮助形成解题思路，使题目内容更加的形象化.

例6 (2017年全国Ⅲ综合题19)四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．证明：平面ACD⊥平面ABC.

解析由题设可得，△ABD≌△CBD，从而AD=DC.又△ACD是直角三角形，所以∠ADC=90°.取AC的中点O，连接DO,BO,则DO⊥AC,DO=AO.又由于△ABC是正三角形，故BO⊥AC.所以∠DOB为二面角D-AC-B的平面角.在Rt△AOB中，BO2+AO2=AB2，又AB=BD，所以BO2+DO2=BO2+AO2=AB2=BD2，故∠DOB=90°.所以平面ACD⊥平面ABC.

数学是高中学习的重点科目，学生需要掌握一定的基础知识和解题技巧，这样才能够提高解题速度和效率，在高考中获得较高的分数.教师应该分析高考试卷并积累一定的解题技巧，并将其教给学生，让学生在答题时能够又快又准.