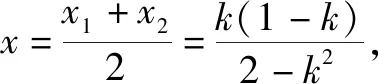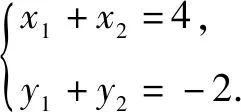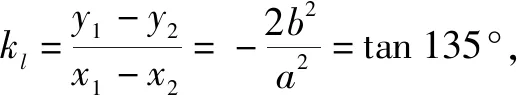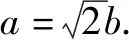三叉星示意图在高中数学中的应用
李清财
(福建省南安市南星中学 362342)
笔者要介绍三叉星示意图如图所示:

当中有三个对象,只要满足其中两个条件,就可以得到第三个结论,即知二求一.利用三叉星示意图可以把抽象推理过程化为直观,有助于学生对概念和定义的理解;有助于学生在解决实际问题中进行条件的分析,进一步确定转化方向;有助于学生归纳总结题型.以下是利用三叉星示意图的教学案例.
一、利用三叉星示意图,加深对概念和定义的理解,知道化归与转化的方向
案例1 一般地,设函数f(x)的定义域为I,区间D⊆I:如果∀x1,x2∈D,当x1 概念的前提与结论利用三叉星示意图呈现,如下图: 由满足其中的两个条件,就可以得到第三个对应的结论,体现函数单调性的用法,加深对概念的理解.例如: A.f(3) C.f(2) 问题2 函数y=f(x)在R上单调递增,且f(m2)>f(-m),求实数m的取值范围. 分析由已知可得m2>-m,解得实数m的取值范围为(-∞,-1)∪(0,+∞). 案例2 在高中数学必修一第一单元集合中,涉及两个集合的基本运算和包含关系,利用三叉星示意图可以展示解决问题的方法. 而上面三者,知二求一,都可以利用数轴法进行处理. 问题3 已知集合M={x|-3 A.{x|x<-5或x>-3} B. {x|-5 C. {x|-3 分析集合M与集合N如图所示: 所以M∪N={x|x<-5或x>-3},故答案:A. 问题4 设S={x|x<-1或x>5},T={x|a A. -3 C.a≤-3或a>-1 D.a<-3或a>-1 分析集合S和集合T如图所示: 案例3 大部分学生比较难于掌握高中解析几何,在高考中往往在这一部分丢分较多,问题出现在于读题和分析题目困难.利用三叉星示意图,帮助学生对条件的分析,确定化归与转化的方向,有利于学生掌握数学方法和归纳题型.例如直线f(x,y)=0与曲线φ(x,y)=0的弦的中点Q(x0,y0)问题. (2-k2)x2-2k(1-k)x-(1-k)2-2=0(2-k2≠0)① 解得k=2. 当k=2时,方程①成为2x2-4x+3=0, 根的判别式Δ=16-24=-8<0,方程①没有实数解. 所以,不能作一条直线l与双曲线交于A,B两点,且点P是线段AB的中点.
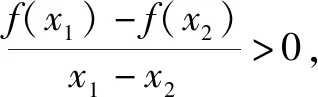

二、利用三叉星示意图,帮助学生对条件的分析,有利于数学方法的总结

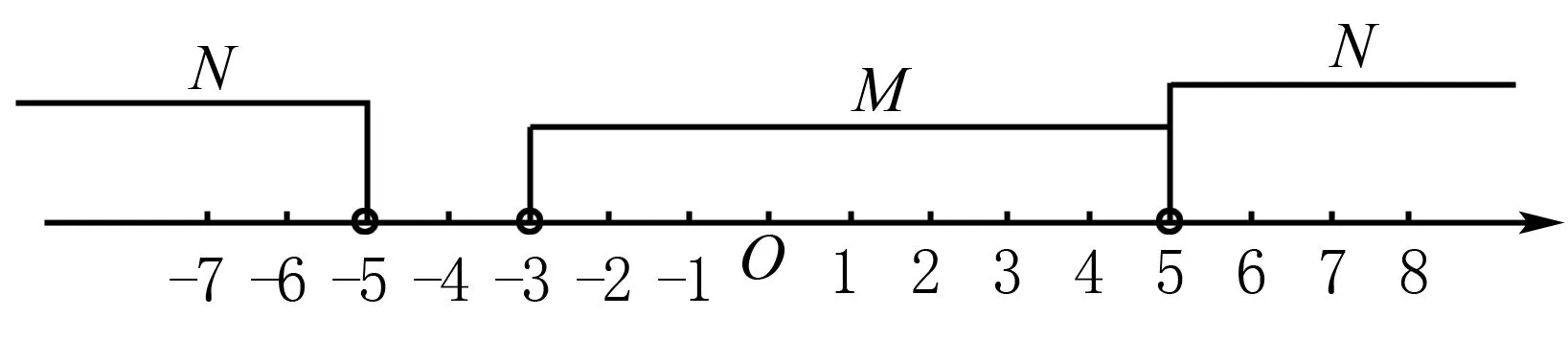
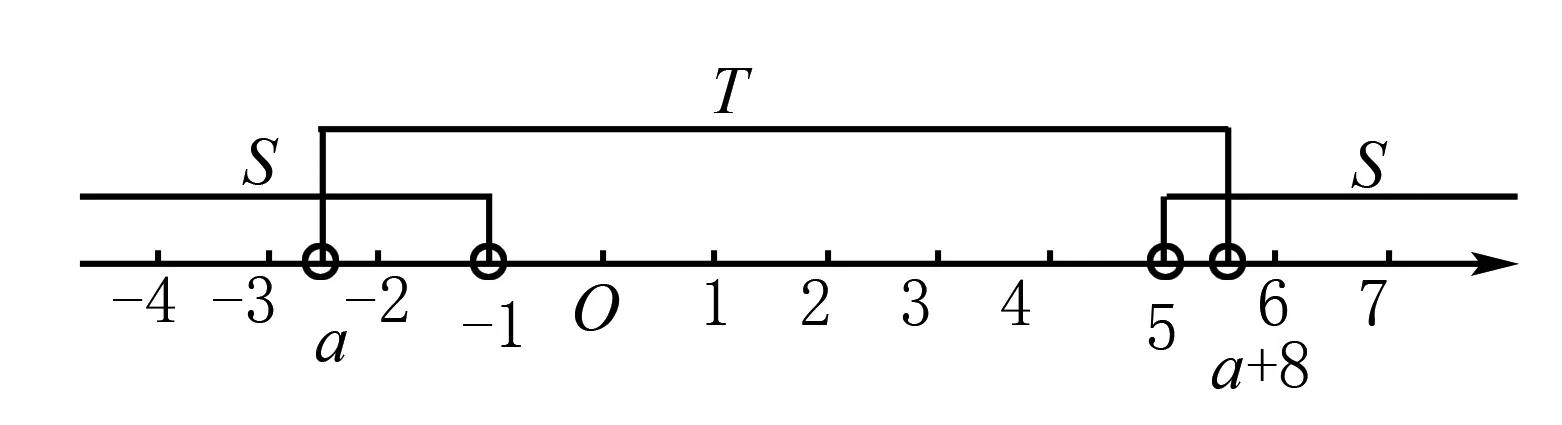

三、利用三叉星示意图,帮助学生对条件的分析,有利于学生掌握数学方法和归纳题型