含有指数函数的Riccati微分方程通解的充要条件

戴 伟，叶永升

（淮北师范大学 数学科学学院，安徽 淮北235000）

0 引言

Riccati微分方程

其中：P(x)，Q(x)和R(x)为连续函数. 此方程于1841年被法国数学家刘维尔证明了没有初等解法，但是人们通过适当的变换可以把它化为可解的方程类型，然后再代回原来的变量得到Riccati微分方程的解.或者根据P(x)，Q(x)和R(x)之间的关系寻找具有特殊形式方程（1）的解. 在文献［1]中，已知方程（1）的一个特解yˉ(x)，通过变换y=z+yˉ，方程（1）就可化为关于变量z的伯努利（Bernoulli）方程. 而在文献［2-11]中，当P(x)，Q(x)和R(x)满足一定条件时，方程（1）也可以通过初等积分法求解. 文献［12-15]介绍利用变量变换法求解微分方程的技巧. 由此，本文利用变量变换法，当P(x)，Q(x)和R(x)满足一定条件时，给出一类Riccati微分方程存在通解的充要条件.

1 主要结果及其证明

引理1［1]设伯努利（Bernoulli）方程为其中：P(x)和Q(x)是连续函数. 则此方程的通解为

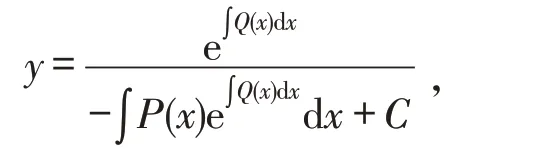
其中C为任意常数.

定理1Riccati微分方程（1）存在形如

证明为证明方便，设

必要性. 设方程（1）的通解为式（2），则将式（2）代入式（1）得

整理得

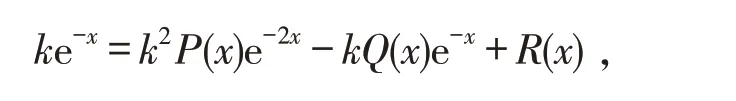
即

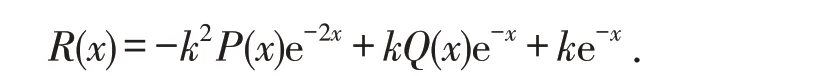
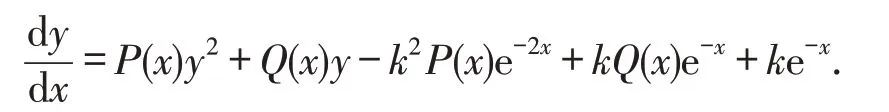
显然，y=-ke-x是方程（3）的解.

设z=y+ke-x，则方程（3）可变为由引理1得，

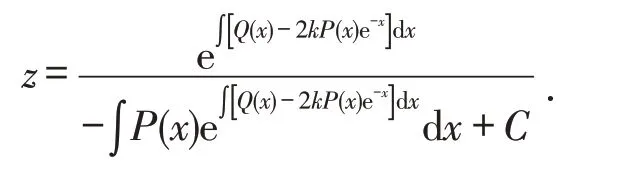
即

y=-ke-x+为任意常数.

类似可得下面定理.

定理2Riccati 微分方程（1）存在形如的通解充要条件为其中：k为常数，C为任意常数.

根据定理1和定理2，我们可得下列2个推论.

推论1若Q(x)=2kP(x)e-x，R(x)=k2P(x)e-2x+ke-x，则Riccati微分方程（1）存在形如

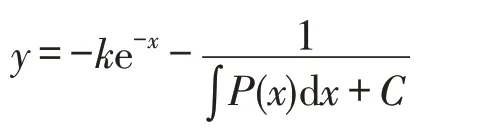
的通解，其中：k为常数，C为任意常数.

推论2设Q(x)=2kP(x)ex,R(x)=k2P(x)e2x-kex，则Riccati微分方程（1）存在形如的通解，其中：k为常数，C为任意常数.

2 应用举例

例1求微分方程的通解.

解这里P(x)=4x3,Q(x)=8x3e-x,R(x)=4x3e-2x+e-x，显然

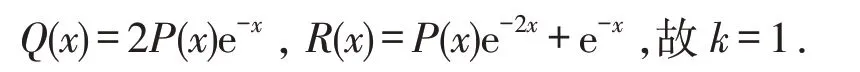
由推论1可知方程的通解为其中C为任意常数.

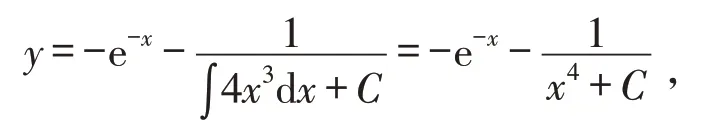
例2求微分方程的通解.

解这里P(x)=cosx,Q(x)=4excosx,R(x)=4e2xcosx-2ex，显然故k=2.

由推论2可知方程的通解为

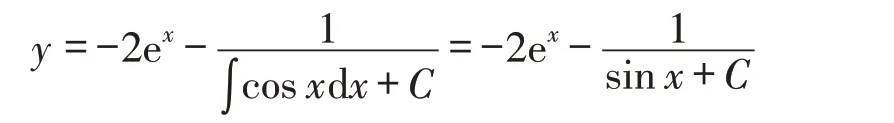
其中C为任意常数.