一类非周期互补序列的构造

赵 敏，王敬敬，杨志耀，郭宇燕，卓泽朋①

（淮北师范大学 数学科学学院，安徽 淮北235000）

0 引言

1961年Golay［1]首次提出互补序列的概念，并将互补序列应用在工程中. 之后，诸多学者对互补序列进行深入研究，使得互补序列对的概念得到进一步推广. 互补序列可分为周期互补序列和非周期互补序列. 互补序列具有理想的相关特性，在雷达、同步、通信等工程中有较为广泛的应用. 同时，非周期互补序列在通信系统中也有着重要应用. 最先提出的二元互补序列是由2个等长的二元序列组成，并且所有异相点的非周期自相关函数均为零. 此类序列最先用于解决多隙红外分光镜的设计问题，之后在导航系统中也得到应用，如罗兰-C导航系统采用的信号形式就是一种二元互补序列.

文献［1-2]表明，互补序列长度N必须满足：（1）N=2a10b26c，其中a，b，c是非负整数，N必须是2个整数的平方和；N一定不包含素因子P=3(mod 4).（2）由N长互补序列构造2N长互补序列的构造方法.（3）由N长互补序列和M长互补序列构造2NM长互补序列的构造方法.（4）由N长互补序列和M长互补序列构造NM长互补序列的构造方法. 近些年，研究表明，交织技术在信道编码上有一定的作用［3]，在信道存在突发差错干扰时，交织技术可显著提高信道编码的性能，使误码率降低1～2个数量级. 文献［4-6]对交织技术在ZCZ序列（Zero Correlation Zone，零相关区序列）集合的构造发挥着极其重要的作用，运用交织技术提出一类新型的接近最优零相关区序列集的构造方法. Tang等［7-11]在序列编码领域做出基础系统性工作，尤其是唐小虎开创零相关区序列新领域，给出周期为N≡2(mod 4)并且具有最佳自相关值的平衡四元序列的构造，以及周期为N≡0(mod 4)并且具有最佳自相关值的几乎平衡二元序列的构造，从而产生更多具有最佳自相关值的序列. Ke［12]构造一类新的具有最优自相关值周期为4N的二元序列，并且导出一个新的几乎差集. 文献［13]给出几个新的具有最优三级自相关的周期为N的二元序列族. 文献［14]通过交织4个合适的Ding-Helleseth-Lam 序列，构造周期为4p的二元序列，这种构造产生新的具有最优自相关值的二进制序列，在以往的研究中是不能产生这种序列的. 文献［15]利用四元正交序列集来构造四元非周期互补序列集. 另外给出2类基于二元正交矩阵的四元正交序列集的构造方法，得到的四元正交序列集可以用于构造四元零相关区非周期互补序列集.

本文基于已有的互补序列，对二元互补序列进行研究. 利用周期为N的二元序列，通过交织运算构造出周期为2N和4N的二元序列. 互补序列对的自相关系数之和能够得到由N长互补序列构造出长为2r×N的互补序列.

1 预备知识

定义1［1]设a和b为2 个周期为N的序列，有则称序列u为序列a和b的交织序列，其中I(a,b)表示向量a和b的交织运算.

定义2［1]设a=(a0,a1,…,aN-1)是周期为N的序列，A={a0,a1,…,aM-1}是M个周期为N的序列的集合，对任意L(i)(a)=(ai,ai+1,…,a0,…,ai-1)，表示序列a的左循环移位运算算子，其中ai=(ai,0,ai,1,…,ai,N-1)，0＜i ＜N，规定L(0)(a)=a.

定义3［2]设a和b是2个周期为N的序列，那么函数为序列a和b的非周期互相关函数，这里0 ≤τ ＜N. 特别地，当a=b时，Ra,a(τ)称为序列a的非周期自相关函数，记作Ra(τ).

引理1［5-6]设u和v是两个交织序列，那么u和v矩阵形式表示如下：

令τ=2τ1+τ2（0 ≤τ2＜2），则序列u和v的周期互相关函数表达式如下：

（1）当τ2=0 时，

（2）当τ2=1时，

定义3［2]设a和b为周期为N的2个二元序列，非周期自相关函数分别为Ra(τ)和Rb(τ)，那么有

则a和b为一互补序列对.

2 主要结果

定理1设是周期为N的二元序列，当a，b是周期互补序列时，则序列是周期为N的非周期互补序列，这里元素取1和-1.

证明对序列u，v进行交织运算得：

由引理1，令τ=2τ1+τ2,0 ≤τ2＜2，计算u和v自相关值，有

（1）当τ2=0 时，

故Ru(τ)+Rv(τ)=0.

（2）当τ2=1时，有

所以

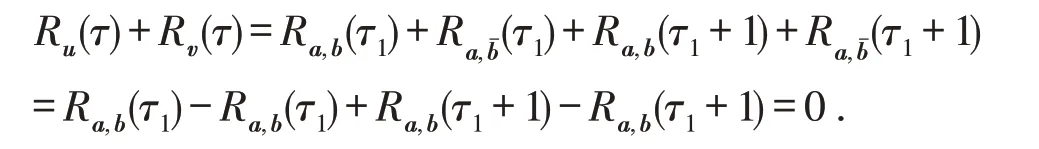
所以u，v为非周期互补序列.

定理2设是周期为N的二元序列，当a，b是周期互补序列时，则序列是非周期互补序列，这里元素取1和-1.

证明由定理1可知是周期互补序列，令

由交织运算有

令τ=4τ1+τ2(0 ≤τ2＜3)，

（1）当τ2=0 时，有

得Rs(τ)+Rt(τ)=0.

（2）当τ2=1时，有

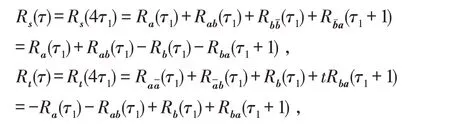
得Rs(τ)+Rt(τ)=0.

（3）当τ2=2 时，有

得Rs(τ)+Rt(τ)=0.

（4）当τ2=3 时

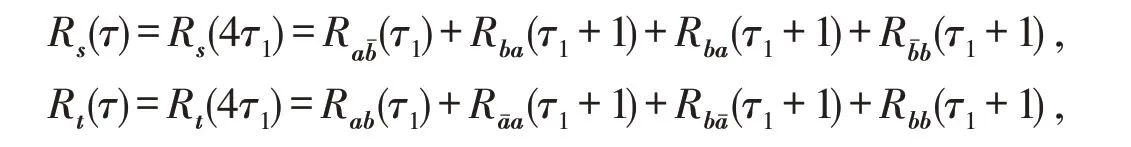
得Rs(τ)+Rt(τ)=0. 因此s和t是非周期互补序列.

通过定理1 和定理2，可以由长为N的互补序列构造出长为2r×N的互补序列，其中r为任意正整数.

3 结论

本文基于已有的互补序列，对二元互补序列进行研究. 通过矩阵的形式，利用交织技术以及已有的非周期互补序列对，得到新的非周期互补序列对. 互补序列对的自相关系数之和能够得到由N长互补序列构造出长为2r×N的互补序列. 本文提出的构造方法，与已有的方法相比，对互补序列对的选取比较特殊，参数要求相对宽松，构造过程较为简洁，具有可实现性.