基于灰关联的双极二元语义动态群决策模型及应用

牛翠萍，张 娜①

（1.淮北师范大学 数学科学学院，安徽 淮北235000；2.石河子大学 经济与管理学院，新疆 石河子832000；3.北京大学 光华管理学院，北京100871）

0 引言

在如今大数据时代下，各式各样的信息大量地充斥着网络，为决策者提供充足的基本决策信息的同时，也为政府和企业的决策过程带来较大的困难. 此外，由于决策信息的繁杂与其本身普遍存在的模糊性，导致决策结果的合理性与有效性也受到较大的挑战.

二元语义决策方法在处理模糊性决策信息的问题上具有独特的优势，近年来其理论与方法应用得到广大学者的持续关注和研究. 迄今为止，针对群决策过程中存在多个时期的动态评估问题，学者们提出多阶段动态群体决策模型［1-2]，其中基于二元语义的动态群决策的主要研究成果集中在动态优化模型［3-7]和动态信息集结模型［8-11]. 这些模型的研究核心主要集中在评价指标权重的确定、决策者权重的确定、时间权重的确定以及阶段信息的一致性问题. 但是，在考虑事物发展规律的基础上基于二元语义集结多个时间节点信息的动态群决策研究文献较少且不够系统，随着互联网的高速发展，各种信息异常繁杂且瞬息万变. 因此，有必要进一步研究能够适应如今信息繁杂情形下的复杂语言型决策问题. 本文构建的基于灰关联的双极二元语义动态群决策模型对此类决策问题的解决具有重要的理论意义与现实参考价值.

1 基本概念界定

1.1 双极语言术语集和语义

双极语言术语集表示该集合中语言变量的下标是以零为中心. 如(n为正整数），即为一个对称的双极语言术语集，si为该集合的语言变量. 而0,…,-0.5(t-2),(t-1)}（t为正整数）为非对称的双极语言术语集. 一般情况下选取对称的双极语言术语集进行评价.

定义1［12]给定一个双极语言术语集S={s-n,…,s-1,s0,s1,…,sn}，d为S中的语言变量si集成运算所得，d∈[-n,n]，设i=round(d)，i∈{-n,…,-1,0,1,…,n}，αi=d-i，αi∈[-0.5,0.5)，则将αi称作为si的符号转移变量.

基于定义1，将(si,αi)记作双极二元语义模型，其中：si∈S，αi∈[-0.5,0.5)，实数αi是集合S中的语言变量si运算所得d与S中最贴近的si之间的偏差.

1.2 双极二元语义模型及与实数的互换

一般在决策过程中，给出的语言信息具有模糊性，因而不能直接对语言信息进行整理计算，需要将语言信息转换为实数进行求解. 转换为区间上的实数可通过如下双极二元语义模型实现：

图1 双极二元语义转换为实数

图1 中，Δ-1为双极二元语义(si,αi)化为[-n,n]上实数d的函数，计算详见定义2；δ表示将区间[-n,n]上的实数d转化为[-1,1]区间上的双极二元隶属度(si,μsi(x))，其中：si∈S，μsi(x)是由双极语言变量si∈S的隶属函数μsi得到的隶属度，κ表示将[-1,1]区间上的双极二元隶属度(si,μsi(x))转化为[-1,1]区间上的实数v.

定义2给定双极语言术语集S={s-n,…,s-1,s0,s1,…,sn}，将d∈[-n,n]转化为双极二元语义的函数Δ可定义为：

式（1）中的round(*)表示四舍五入取整算子.

在[-n,n] 中的任一实数d，都存在一个双极二元语义(si,αi) 与之对应. 设αi∈[-0.5,0.5)}是一个双极二元语义集，双极二元语义化为数值d∈[-n,n]函数Δ-1为：

故可知，对任一双极二元语义(si,αi)∈Ht，在[-n,n]中存在一个实数d与之对应. 当(si,αi)依次为(s-n,0),…,(s-1,0),(s0,0),(s1,0),…,(sn,0)时，对应的d分别为-n,…,-1,0,1,…,n.

2 基于灰关联的双极二元语义动态群决策模型的决策步骤

在动态群决策过程中，最重要的环节是确定各阶段的权重和各位决策者的权重. 本文参考现有文献中确定各阶段权重的方法，并将其与灰色关联分析的理论相结合，将二元语义时间权重模型改进为双极二元语义时间权重确定模型进行求解，根据计算得到的时间权重和决策者权重以及事前确定的准则权重集结得到群单阶综合决策矩阵，进一步对双极二元语义动态群决策进行研究. 基本步骤如下：

步骤1：将语言评价信息表转换为双极二元语义决策矩阵.

根据备选方案及其准则得到如下语言评价信息的决策表，并将其转换为对应的双极二元语义决策矩阵(k=1,2,…,l;t=1,2,…,q;i=1,2,…,m;j=1,2,…,n)：

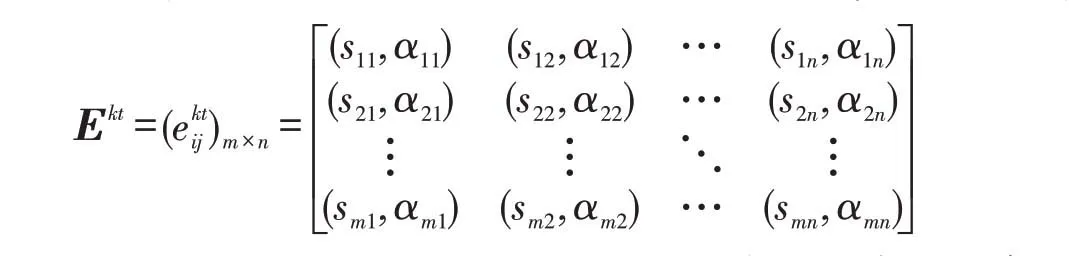
其中，eij∈Ht={(si,αi)|si∈S,αi∈[-0.5,0.5)}是双极二元语义，表示专家ekt对方案Ai在准则zj下第t阶段的语言评价值. 矩阵中的行表示被评估的方案，列表示评估依据的准则指标.

步骤2：分析各阶段专家评价质量.

通过判断方法判定专家评价是否稳定和存在分歧，以及动态决策过程中是否存在质变过程.

定义3［13]（质变阶段） 质变指某个事物在逐渐发展过程中突然发生根本性的变化，若对某个方案各指标的评价在第t阶段和上阶段t-1比较存在较大变化，即

则称阶段t为质变阶段.

通过定义3的判断方法可从动态变化的角度分析事物的发展情况，便于对长期的决策问题作出合理的决策方案. 本文研究的前提假设是专家所作决策均为理性决策，并通过5粒度语言评价集对各方案各指标作出评价，式（3）表示如果某方案在相邻的2个阶段，各个指标变化均超过2个度，即可判断此方案在该阶段发生质变. 在实际决策中，决策者可根据所使用语言评价集的不同以及实际决策情况适当选取判断发生质变的“度”.

针对在动态发展过程中发生质变的方案，若只发生一次，则决策评价阶段为发生质变后的各阶段；若多次发生质变，则决策评价阶段选择最后一次质变后的各阶段. 针对在整个决策评价的各阶段内均未发生质变的方案，先对各阶段赋予相应的权重，然后对该方案在各阶段的表现进行加权综合评价.

步骤3：确定各阶段权重.

本文确定各阶段时间权重的详细步骤如下：

1）阶段综合评价矩阵的构建. 为对各方案在所有阶段内的表现进行综合评价，需要知道各阶段权重. 然而通常情况下不易获得关于各阶段权重的先验信息，本文选用几何指数方式赋予各阶段初始权重，然后将各专家各阶段的评价矩阵通过加权求和集结出综合评价矩阵然后测算各个决策者各阶段的决策矩阵与综合矩阵的关联度，以分析各阶段之间的关系.

2）阶段关联度的计算. 本文采用灰色关联分析法［14]计算各阶段间的关联度. 对于方案Ai(i=1,2,…,m)，将综合评价矩阵看作系统特征行为序列看作系统行为序列. 再将决策者各阶段各方案的评价值与上述集结的综合决策矩阵的评价值进行方案与方案的灰关联分析，可得决策者各阶段各方案的灰色关联度

3）基于关联度确定各阶段时间权重. 为使各阶段的评价信息尽可能充分地反映到整体评价中，从而使各阶段间的差异对整体评价造成的差异达到最小，本文基于所得的平均综合灰关联度，以使得各阶段间关联度偏差达到最小为目标，建立求解各阶段权重的模型：

其中：γkt和γks分别为专家k在阶段t和阶段s的平均综合灰关联度，λkt和λks为专家k在阶段t和阶段s的阶段权重；约束条件λkt≥ζ是用来确保各阶段的评价信息都能对整体决策具有一定的贡献，其中ζ ＞0，a≥1，本文取值ζ=1/aq，q为阶段个数，a=2，表示各阶段中权重的最小值是各阶段权重算术平均值的一半；另外2个约束条件使得阶段权重分别满足归一化和非负性的基本要求.

求解上述规划模型得到各阶段权重λkt，从而可利用式（4）将多阶段决策评价信息集结成单阶段决策信息

步骤4：确定决策专家的权重wk(k=1,2,…,l)，并通过式（5）把第4步得到的各决策专家单阶段决策信息集结为群单阶段决策信息，称为群决策综合信息集.

其中ωj为事前确定的准则指标权重.

步骤5：计算各方案集结结果对应的可靠度δi.

根据所得的决策者ek对各决策方案信息集结值相对应的语言信息灰度vkt ij、各准则权重ωj、各决策专家的综合权重wk，各阶段时间权重λkt可得到决策方案的最终集结结果可靠度为：

临界值一般取δ ＞0.5. 如果由式（6）得δi≤δ，表明决策方案Ai最终集结结果的可靠度较低，需要决策专家重新调整对该方案的评价信息；若δi ＞δ，则对决策方案进行排序.

根据上述计算所得的各方案群综合决策信息集E和对应的各方案集结结果可靠度δi，计算各决策方案的最终集结结果，即并依据以下规定进行排序：对于决策方案i和j，通常有9 种情况：1）ei ＜ej,δi ＜δj；2）ei ＞ej,δi ＞δj；3）ei ＞ej,δi ＜δj；4）ei ＜ej,δi ＞δj；5）ei ＜ej,δi=δj；6）ei ＞ej,δi=δj；7）ei=ej,δi ＞δj；8）ei=ej,δi ＜δj；9）ei=ej,δi=δj.

可见，1）、5）、8）的情况，有i≺j；2）、6）、7）的情况，有i≻j；9）的情况，有i⇔j；3）、4）的情况，可以进一步构造隶属度函数相互比较.

3 案例研究

以精准扶贫过程中的产业扶贫项目选择为例，如果决策专家将对产业扶贫项目的预期经济效益（Z1）、环境影响（Z2）、对相关产业的带动作用（Z3）、解决地区就业（Z4）和项目引进可持续度（Z5）5个准则来对项目进行3次年度评估. 为使决策结果全面合理，决策专家组由扶贫办的相关专家1名（E1），发改委相关专家1名（E2），深度贫困地区发展研究相关专家1名（E3）以及产业扶贫项目组的相关专家1名（E4）构成. 对于某深度贫困地区项目，现有3 套方案可供选择. 则事件集为其中A1,A2,A3代表3套不同的方案. 决策者针对各方案在所有准则下的评估值、准则权重值等依旧都以语言形式给出，等级评价集S={VG,G,M,P,VP}，分别代表｛很好，好，一般，差，很差｝，信息量语言集为M=｛M1=很充分，M2=较充分，M3=一般，M4=较贫乏，M5=很贫乏｝. 决策者给出所有方案全部准则下各阶段的语言评价信息及对应的信息量语言集分别见表1、表2和表3. 请对这3个方案进行全阶段综合评估并选出一个最适合某深度贫困地区发展的脱贫产业.

表1 各专家对各方案第1阶段的语言评价信息表

表2 各专家对各方案第2阶段的语言评价信息表

表3 各专家对各方案第3阶段的语言评价信息表

（1）把上述决策者提供的所有方案的语言评价信息表转换成对应的双极二元语义阵(k=1,2,3,4;t=1,2,3;i=1,2,3;j=1,2,3,4,5)（限于篇幅此处略去），其中，eij∈Ht={(si,αi)|si∈S,αi∈[-0.5,0.5)}是双极二元语义，表示专家ekt对方案Ai在准则zj下第t阶段的语言评价值. 矩阵中的行表示被评估的3个方案，列表示评估依据的5个准则.

（2）进行阶段内和阶段间评价质量分析. 按定义3的方法分析专家的判断质量，计算得到：

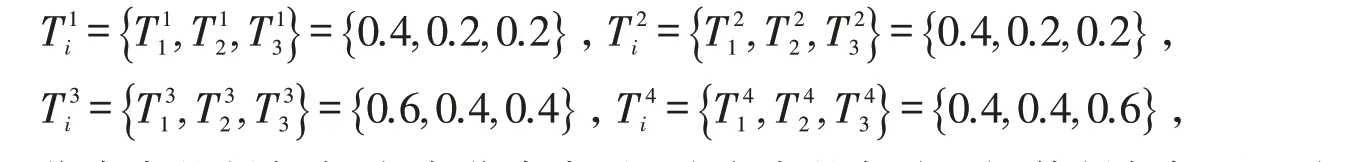
从4 位专家的判断来看，各位专家对3个方案的各阶段评估判断都属于稳定判断；从各个专家对各个方案的评价来看，显然各方案全阶段只是处于量变阶段.

（3）确定各阶段权重. 阶段综合评价矩阵，令其权重ω=0.4，其余q-1 阶段的初始权重分别为(1-ω)/(q-1)=0.3，将各决策专家各阶段的评价矩阵通过加权求和集结出阶段综合评价矩阵然后分别计算4位决策专家对各方案在各阶段作出的评价信息矩阵与阶段综合评价矩阵的灰关联度，最后依据公式求得平均综合灰关联度.

1）根据上述平均综合灰关联度的值确定各阶段权重. 依据模型（M-1），运用Lingo求解得到各专家各阶段时间权重为：

2）基于上述解得的阶段权重，通过式（4）将4 位决策专家的3 阶段评价信息集结为单阶段评价信息..

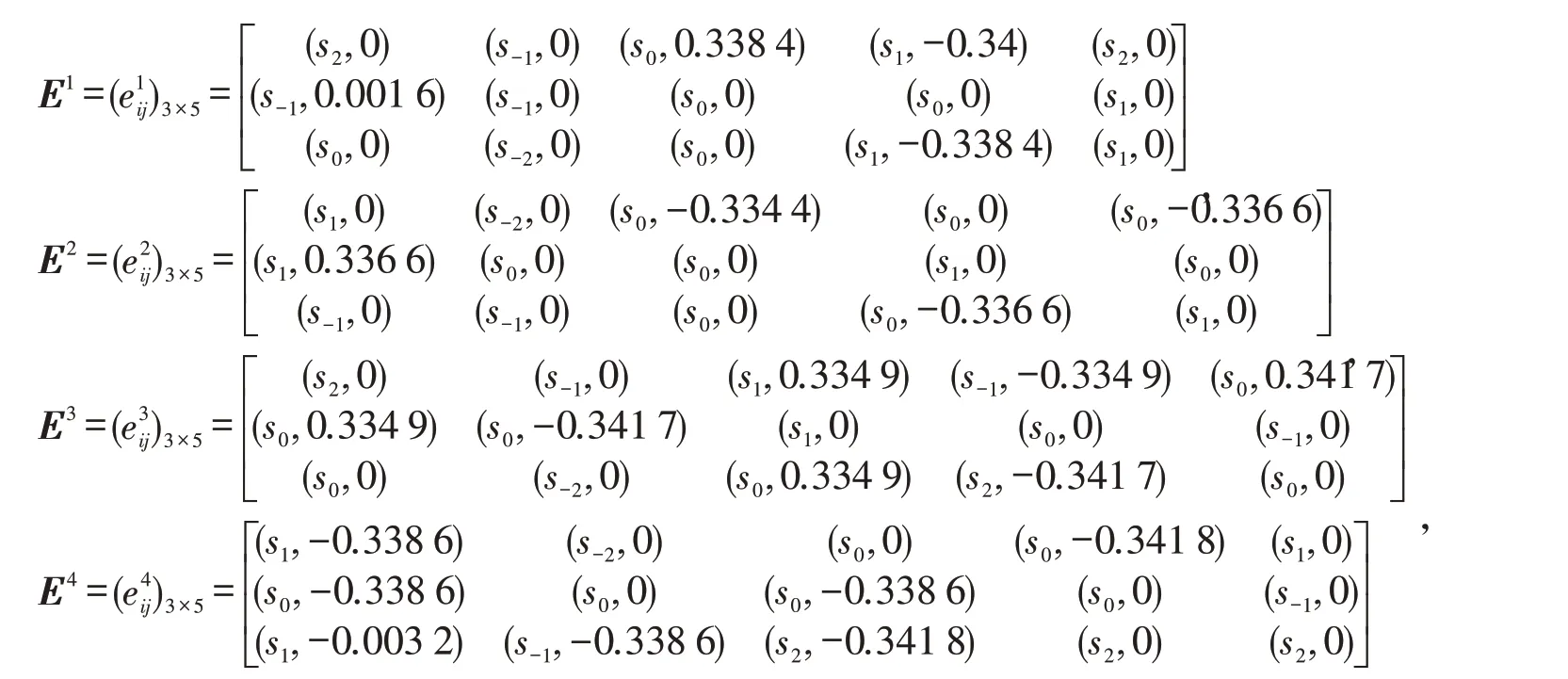
（4）通过考虑专家一致性、信息可靠性以及先验主观权重得到决策者综合权重［15]，求得最终综合权重为wk=(0.2580,0.2486,0.2495,0.2439). 根据式（5）将各专家单阶段的信息集结成群综合决策信息集，其中ωj为事前确定的准则指标权重，即ωj=(0.2667,0.3000,0.0756,0.1243,0.2334). 则求得各方案群综合决策信息集E={0 .1039,-0.0943,-0.0865} .

（5）计算各方案集结结果对应的可靠度δi并排序.

根据式（6）分别计算得到决策方案的最终集结结果可靠度为δ1=74.01%，δ2=69.98%，δ3=71.56%. 设定临界值δ=0.65，均满足δi ＞δ，故可对集结结果进行排序.

根据上述所得的各方案综合决策信息集E和对应的各方案集结结果可靠度δi，得到各决策方案的最终集结结果即=(0.1039,0.7401)，=(-0.0943,0.6998)=(-0.0865,0.7156)，显然可以得出：A1≻A3≻A2，即这3个方案中最适合某深度贫困地区发展的脱贫产业为方案A1.

4 结论

在灰关联理论基础上对语言型双极二元语义多准则动态群决策问题进行研究的过程中，各阶段时间权重的确定非常关键，需要与决策对象自身的变化情况相切合. 因此，构建出将基于灰关联的多阶段时间权重确定模型与双极二元语义模型相结合的决策方法. 该模型具有以下几个特点：（1）该模型在进行决策分析之前，首先对专家提供的评价信息进行质量分析. 给出测定各决策专家评价信息质量的指标以及决策方案在各阶段是否发生质变的判断方法，尽可能地避免无效决策情况的发生.（2）引入灰关联分析理论，构建多阶段时间权重确定模型，不仅包含信息的新旧更替，而且充分利用各阶段的信息特征，使得专家对各决策方案的整体评价最大程度地吸收原始信息，提高决策结果的准确性.（3）本文所建模型更适用于实践中的长远决策. 在现实情况下，由于决策问题的复杂性，通常存在2种决策方式：快速决策和长远决策. 本文提出的多阶段语言评价信息集结方法即是适用于长远决策，实用性更强.