环R+vR+v2R 上的斜常循环码
王艳萍①
(宿州学院 数学与统计学院,安徽 宿州234000)
0 引言
1994 年Hammons 等人研究二元线性码[1]. 近些年,很多学者将重点转移到有限环上,研究各类有限环如有限链环、非链环等各类环上的循环码、常循环码等[2-6];渐渐地,斜循环码、斜常循环码也被广泛研究. 比如文献[7-12],通过研究斜多项式环、进而构造自同构,以用来讨论对应环上的斜循环码的若干性质;在文献[13-15]中,分别探讨各类不同环上的斜常循环码,从而得到相关的性质. 本文首先介绍环R+vR+v2R(v3=v)上的一个Gray 映射,研究环上码的一些性质;然后,给出环上的斜常循环码,并证明环上码的充要条件;最后,在给出一些特定的条件下,探究环上对偶码的若干性质. 本文的研究为代数编码理论提供一些理论依据.
1 预备知识
令ℜ=R+vR+v2R={x+vy+v2z|x,y,z∈R},其中v3=v,且环R是以<λ >为极大理想;p为奇数,它是剩余域的特征. 若无特殊说明,下文出现的环ℜ 即为环R+vR+v2R. 设环R是有限链环,易得环ℜ 并不是有限链环.
设e1=2-1v+2-1v2,e2=-2-1v+2-1v2,e3=1-v2,可知e1,e2,e3是环ℜ 上两两相互正交,且它们为幂等元,而<e1>={e1a|a∈ℜ} ,<e2>={e2a|a∈ℜ} ,<e3>={e3a|a∈ℜ} 是 环ℜ 上 的3 个 相 互 互 素 的 理 想,则ℜ ≅ 对∀X,Y∈ℜn,X=(x1,x2,…,xn) ,Y=(y1,y2,…,yn) ,定 义 内 积:X∙Y=x1y1+x2y2+…+xnyn,如 果X∙Y=0,称X,Y正交. 对于环ℜn上的线性码C,则它的对偶码:C⊥={x|x∙y=0,∀y∈C},如果C=C⊥,称C为自对偶码. 并定义: 则由文献[16]可知:(1)C1,C2,C3为R上的长为n的线性码;(2)C=e1C1+e2C2+e3C3,且这种表示是唯一的. 定义φ:ℜ →R3,对∀c=e1x+e2y+e3z∈ℜ,x,y,z∈R,有φ(c)=(x,y,z),且wL(c)=wH(x,y,z). 将φ扩展成Φ:ℜn→R3n,对∀c=(c0,c1,…,cn-1)∈ℜn,有 定理1C为ℜ 上长是n的线性码,则有: (1)C⊥也是环ℜ 上的线性码; (2)Φ(C)= (3)Φ(C⊥)= 定义1如果对∀c=(c0,c1,…,cn-1)∈C有: 此时定义中的为环ℜ 上的一个自同构,定义中的λ是环ℜ 的单位,而为ℜn上的自同态,则可称C为斜常循环码常循环码). 注1上述中,若λ=1,可称码C是斜循环码;λ=-1,可称码C是斜负循环码. 定义2环ℜ 斜多项式环:其加法运算:一般的加法;其乘法运算则可知是非交换环. 注2如果则可得的左理想,未必是理想. 通过的中心来阐述,也就是对有h(x)∙g(x)=g(x)∙h(x). 引理1设n是N+为上述定义中的自同构,1+v-v2为ℜ 上的一个单位则以下条件是相互等价的:(1)为的理想;(2)xn-(1+v-v2)为的中心. 证明(1)⇒(2) 因<xn-(1+v-v2)>为的理想,则对于∀ax∈ℜ,有 有 即得xn-(1+v-v2)为的中心. (3)⇒(1) 由理想的定义,显然结论成立. 注3(1)下述研究的内容:限制条件为<xn-(1+v-v2)>是的理想;(2)设上述的满足则 其中θ也是环R上的一个自同构. 定理2设C=e1C1⊕e2C2⊕e3C3,则可得:C是θˉ-(1+v-v2)-常循环码⇔(1)C1,C3为环ℜ 上的斜循环码;(2)C2为环ℜ 上的斜负循环码. 证明假设 则 又因 定理3假设有C=e1C1⊕e2C2⊕e3C3,它是环ℜ 上的常循环码,而C1=<g1(x)>,C2=<g2(x)>,C3=<g3(x)>,其中右整除右整除xn+1,g3(x)也右整除xn-1,则可得:存在唯一有C=<g(x)>成立,并且有g(x) 右整除xn-(1+v-v2) , 证明(1)首先证C=<g(x)>. 假设g(x)=e1g1(x)+e2g2(x)+e3g3(x),则C⊆ (2)下面证g(x)右整除xn-(1+v-v2). 因g1(x)右整除xn-1,g2(x)右整除xn+1,g3(x)右整除xn-1,则必存在f1(x),f2(x),f3(x)有 又因 则有 即证结论成立. 即得结论. 假设上述定义的自同构θˉ是2阶的,即并定义下面研究的内容限制条件:(1)是偶数. 定理4码C是环ℜ 上的线性码,则有:C为常循环码⇔C⊥为常循环码. 证明“⇒” 若C为常循环码,则知对∀u=(u0,u1,…,un-1)∈C有 即 得 也就是C⊥为常循环码.“⇐”类似可证. 下述引理2可参照文献[18]类似方法,得出下列性质. 引理2设则下述所给出的结论相互等价: 定理5设C的长度为偶数并且C为常循环码,C=<g(x)>,其中g(x)是首一的多项式,此时则可得 (2)C⊥=且C⊥是常循环码. 证明(1)因所以 本文首先通过构造映射,给出环R+vR+v2R(v3=v)的Gray 映射,研究环上码的一些性质. 然后构造环上的自同构,讨论环上的斜常循环码的性质. 最后给出在特定条件下:(1)长度是偶长度的,(2)所给自同构阶数为2,在这2个条件下的对偶码的部分性质. 为代数编码理论中寻找好码提供很好的帮助.
2 Gray映射
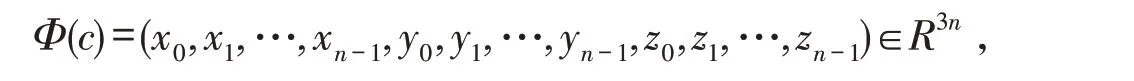
3 斜常循环码




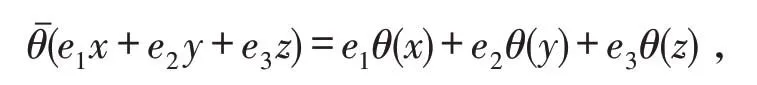
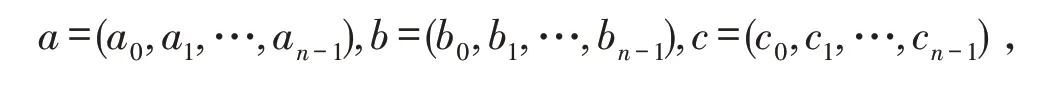
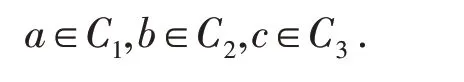
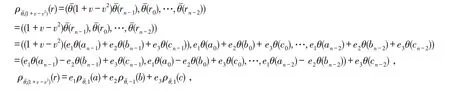
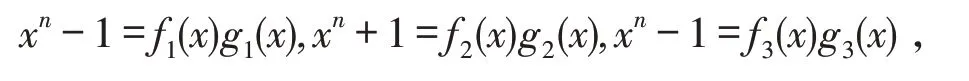
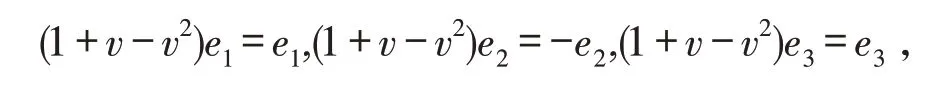


4 对偶码

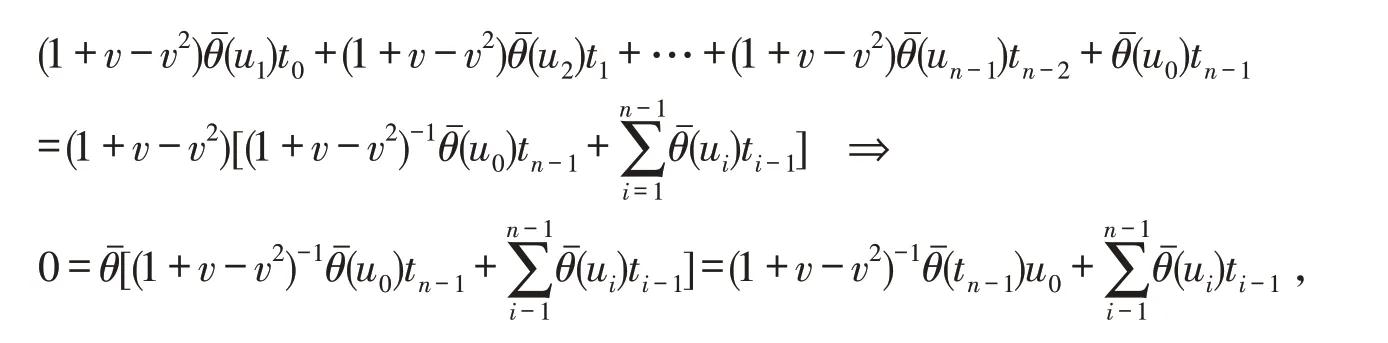



5 小结

