利用GeoGebra求曲边梯形的面积
李伟斌 王新爱
曲邊梯形的面积是人教A版数学选修2-2教材中的一个数学探究实验,借助信息技术创设实验平台,可向学生直观地展示本节课内容中“以直代曲”“极限逼近”的过程,从中体会“分割、近似代替、求和、取极限”的求曲边梯形的面积的基本步骤,建构定积分概念的知识体系.笔者采用的实验平台是GeoGebra 5,现将实验过程实录于下,与各位读者分享.
以课本问题为例:如何求由抛物线与直线所围成的平面图形的面积S?
问题一:如何实现曲边梯形的分割?
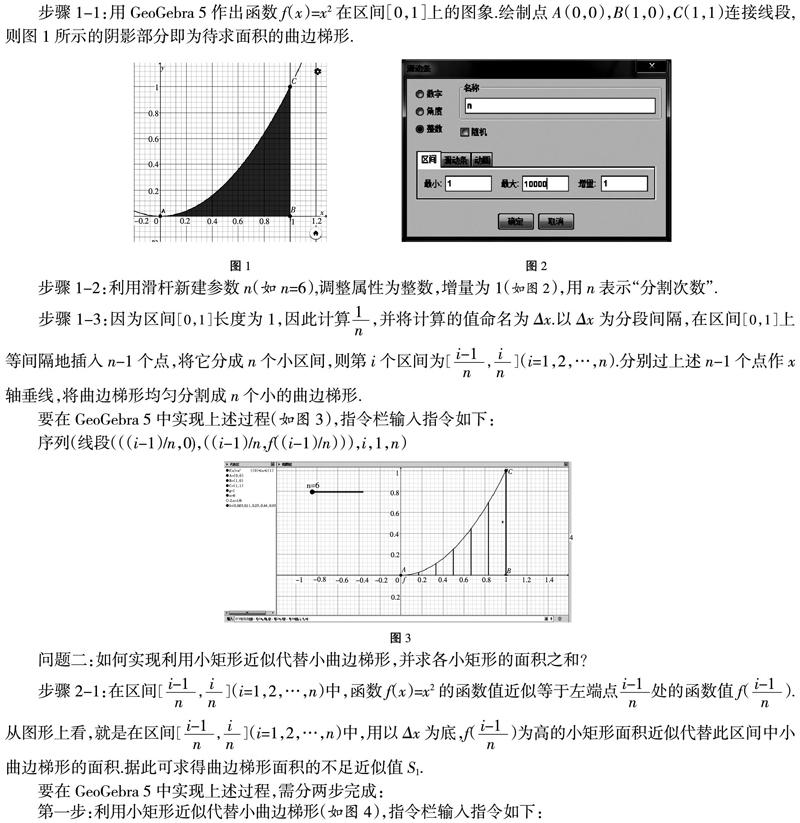
步骤1-1:用GeoGebra 5作出函数f(x)=x2在区间[0,1]上的图象.绘制点A(0,0),B(1,0),C(1,1)连接线段,则图1所示的阴影部分即为待求面积的曲边梯形.
步骤1-2:利用滑杆新建参数n(如n=6),调整属性为整数,增量为1(如图2),用n表示“分割次数”.
要在GeoGebra 5中实现上述过程,需分两步完成:
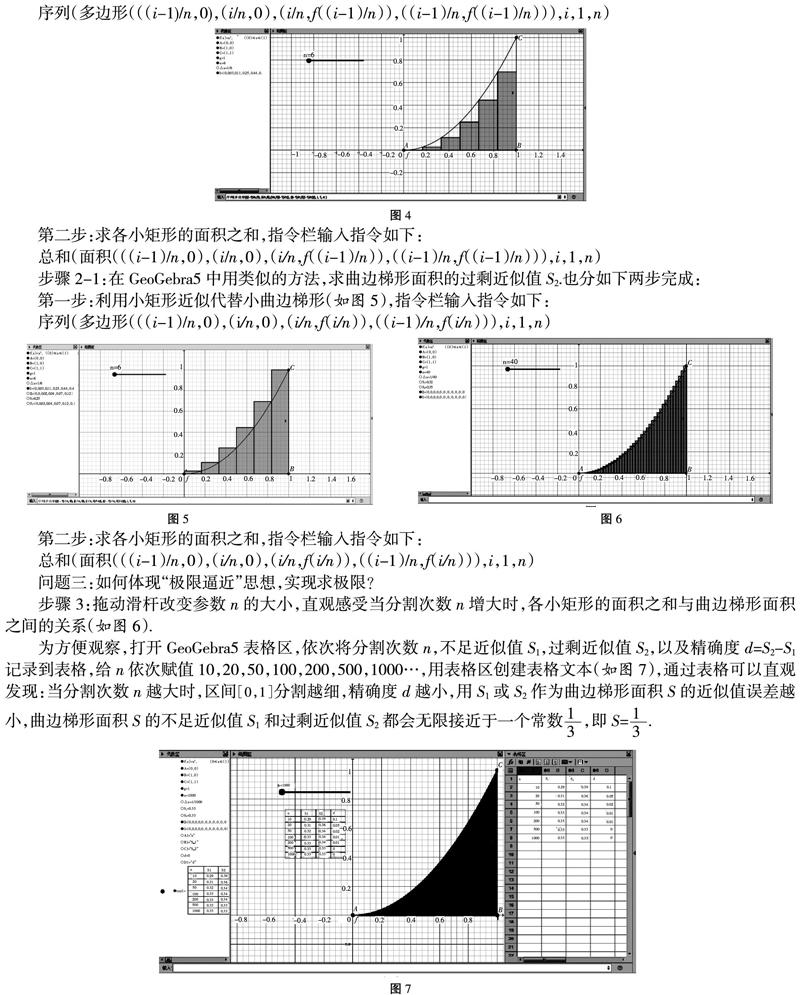
第一步:利用小矩形近似代替小曲边梯形(如图4),指令栏输入指令如下:
第二步:求各小矩形的面积之和,指令栏输入指令如下:
步骤2-1:在GeoGebra5中用类似的方法,求曲边梯形面积的过剩近似值S2.也分如下两步完成:
第一步:利用小矩形近似代替小曲边梯形(如图5),指令栏输入指令如下:
问题三:如何体现“极限逼近”思想,实现求极限?
步骤3:拖动滑杆改变参数n的大小,直观感受当分割次数n增大时,各小矩形的面积之和与曲边梯形面积之间的关系(如图6).
参考文献:
[1]王贵军.GeoGebra与数学实验[M].北京:清华大学出版社,2017.
[2]张加红.曲边梯形面积的《几何画板》构造方法[J].中学数学月刊,2009(3):24-25.
注:本文是兰州市教育科学“十三五”规划2019年度规划课题“新课标背景下基于GeoGebra的高中数学实验的开发与实践”(立项号LZ[2019]GH1212)的成果之一。
编辑 赵飞飞

