一个三角不等式的控制证明与推广

石焕南, 王飞, 王东生

(1. 北京联合大学 师范学院， 北京 100011； 2. 浙江机电职业技术学院 数学教研室，浙江 杭州 310053； 3. 北京电子科技职业学院 基础部， 北京 100176)

0 引言

本文以R表示实数集，x=(x1,…,xn)表示n维实向量，n维实向量的集合记作

R={x=(x1,…,xn):xi∈R,i=1,…,n},

n维正实向量的集合记作

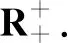
设x=(x1,…,xn)∈Rn,x的初等对称函数是

初等对称函数的对偶形式是

2019年6月，台湾国立高雄师范大学的杜威仕(Wei-Shih Du)教授给我们提供了如下资料，引起了我们的兴趣.

罗马尼亚的Daniel Sitaru提出如下问题：

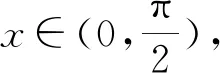
2(sinx)1-sin x·(1-sinx)sin x<1.

(1)

加拿大的Jalil Hajimir利用贝努利(Bornoullie)不等式证明了不等式(1)，阿尔及利亚的Mokhtar Khassani-Mostaganem和罗马尼亚的Remus Florin Stanca分别利用算术-几何平均值不等式和詹森(Jensen)不等式加以证明. 阿塞拜疆的Rovsen Pirguliyev-Sumgait利用詹森(Jensen)不等式证明了不等式(1)的一般形式:

如果a、b>0且a+b=1,那么

(2)

本文将利用受控理论证明不等式(1)，并加以引申和推广. 我们首先给出如下两个定理.

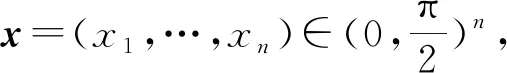
(3)

显然，当n=2时，不等式(3)就化为不等式(1).

(4)

(5)

进一步，将不等式(1)延伸到初等对称函数及其对偶式上，得到如下结果.

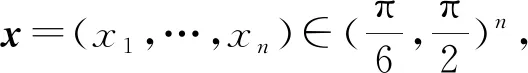
Ek((sinx)1-sin x)=Ek((sinx1)1-sin x1,…,(sinxn)1-sin xn)=

(6)

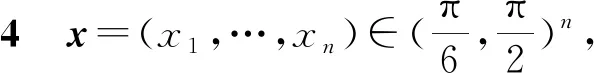
(7)

1 定义和引理

我们需要如下定义和引理.

定义1[1-4]设x、y∈Rn满足

则称x被y所控制，记作xy. 其中x[1]≥…≥x[n]和y[1]≥…≥y[n]分别是x和y的分量的递减重排. 又若x不是y的重排，则称x被y严格控制，记得xy.

注1[1-4]定义1的条件(i)等价于

(8)

定义2[1-4]设x、y∈Rn.x≥y表示对于所有i=1,2…,n有xi≥yi. 设Ω⊂Rn，称φ:Ω→R是一个递增函数，若x≥y⟹φ(x)≥φ(y). 称φ是一个递减函数当且仅当-φ是一个递增函数.

定义3设Ω⊂Rn,φ:Ω→R，若在Ω上xy⟹φ(x)≤φ(y)，则称φ为Ω上的Schur凸函数； 若在Ω上xy⟹φ(x)<φ(y)，则称φ为Ω上的严格Schur凸函数.

我们要用到如下引理.

引理2[1-4]设x=(x1,x2…,xn)∈Rn,则

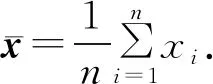
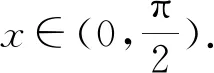
(sinx,1-sinx)(sin2x,cos2x);

(9)

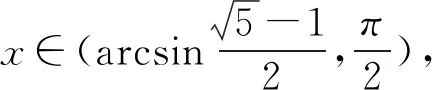
(sin2x,1-sin2x)(sinx,1-sinx).

(10)

证明根据定义1和注1加以证明.

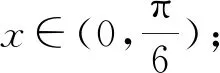
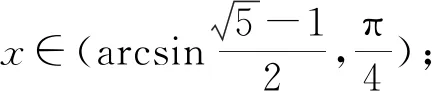
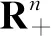
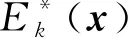
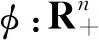
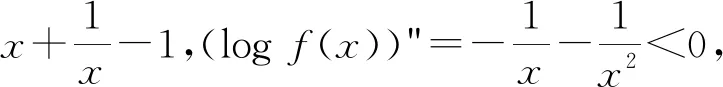
f"(x)=f′(x)(logf(x))′+f(x)(logf(x))"=

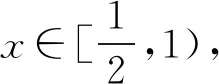
2 定理的证明

从而据引理1,有

证毕.

定理2的证明由引理6,f(x)=x1-x在(0,+∞)上严格对数凹，从而结合引理1、引理2和引理3即可证得定理2.

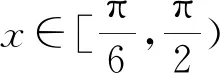
从而结合引理4和引理6即可证得定理3.

定理4的证明类似定理3的证明，可依引理5和引理6证得定理4.

控制关系和Schur凸函数是受控理论的两个最基本的概念，控制关系是向量间的一种较弱的次序关系，Schur凸函数是比熟知的凸函数更为广泛的一类函数，二者的结合是导出不等式的有效方法. 此种方法具有两个鲜明的特点，一是用此法证明不等式往往非常简洁，二是用此法建立不等式常常是“成批”的，它能把许多已有的从不同方法得来的不等式用一种统一的方法简便地推导出来(见文[5-19]).