一种六自由度机械臂的振动特性研究*

梅阳寒，张锐豪，张文龙，刘志伟，刘梓苗

(1.东莞职业技术学院 机电工程学院，广东 东莞 523808；2.广东省东莞市质量监督检测中心，广东 东莞 523808)

0 引 言

我国的机器人工业化起步较晚,水平相对发达国家有一定的差距,主要是在设计理念和应用经验的不足[1]。机器人是个耦合关系复杂的动力学系统,其机械臂由多关节和连杆组成,具有复杂的输入和输出[2-3]。

机械臂相关研究主要有：曾光等[4]提出了一种基于脉冲响应，并利用卷积相关性质获得动态机械臂架结构在不确定性动态激励作用下的振动问题；周恩德等[5]提出了基于ANSYS Work bench简化的机械臂模型，并获得了其前六阶固有频率和振型；LIU等[6]研究了机械臂关节柔度、关节间隙和连杆柔度产生的固有频率,从理论和仿真对机械臂振动进行了深入研究。但由于机械臂关节的传动系统非常复杂,不同联结副之间的边界又难以确定,很难精确地建立模型描述关节的动态特性[7]。

机械臂是机器人运动系统的主要执行部分，其运动的稳定性和精确性将决定机器人末端定位精度。为此,笔者结合MATLAB多自由振动仿真分析软件,利用振动测试分析系统来评估机械臂的动态特性，以力锤激励的振动测试中获得的频率响应函数为基础，提取出机械臂的固有频率[8]，结合单关节运动对末端执行件抖动频率影响分析，为获得机械臂振动逆制的有效策略提供参考依据。

1 机械臂振动传递模型构建

1.1 结构特性分析

机器人机械臂执行的动作主要是由6个轴共同完成，机器人机械臂结构模型如图1所示。

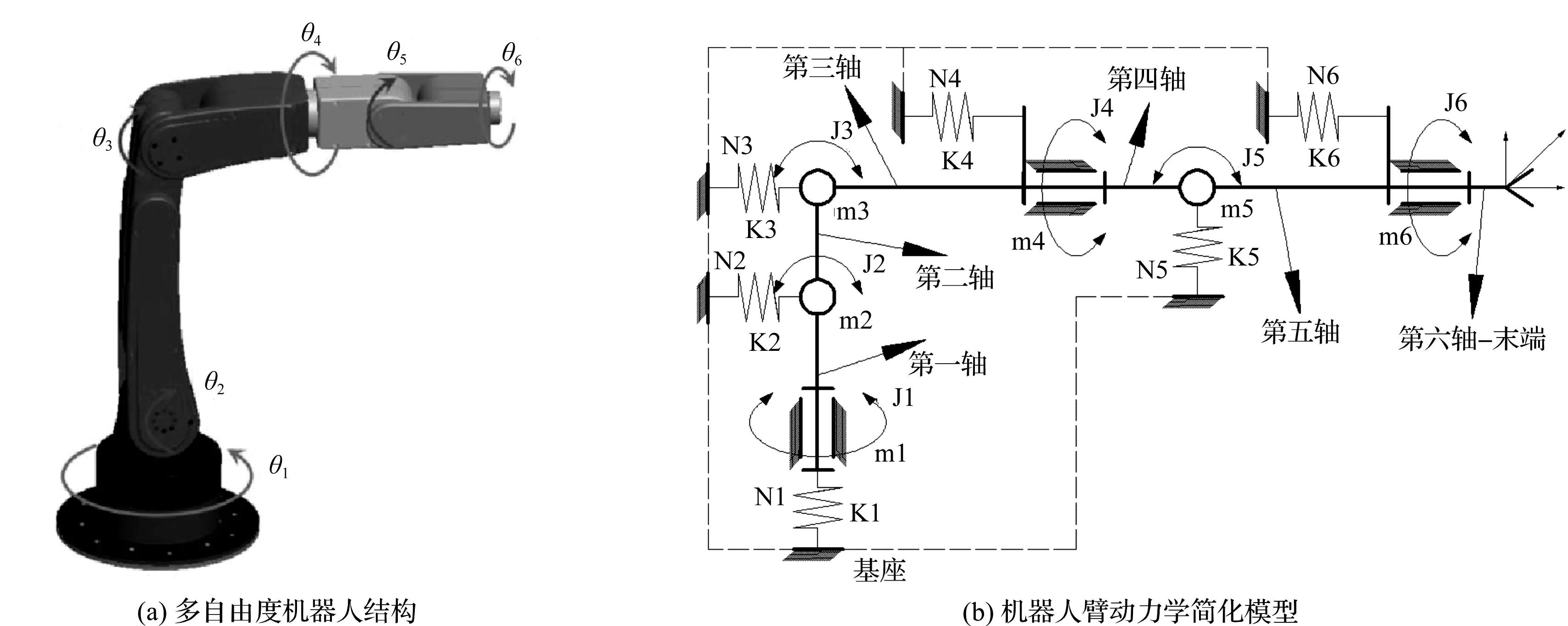
图1 机器人机械臂结构模型

图1中，第一、二、三轴的运动基本确定了末端执行件的空间位置，第四、五、六轴的运动主要用来控制末端执行件的空间姿态。其中，轴一承担机械臂的旋转运动，轴二执行结构整体大范围的俯仰动作，轴三主要完成臂关节的俯仰运动，前三轴完成的动作所需的动能较大，主要使用大功率电机驱动；轴四完成小臂的旋转运动，轴五完成腕部的俯仰动作，最终末端执行结构微调动作主要由第六轴来完成，后三轴所需动能都相对较少，都使用小功率电机。

在机器人机械臂动力学建模过程中，为了减少外部因素对系统分析的影响，本文对各关节结构作一些质量等效处理，使结构处于一种理想状态；把各关节臂等效为质量均匀的杆件，各个关节质量进行集中等效质量处理，集中质量法是用集中于结构节点上的质量代替结构离散的分布质量，把结构分离成围绕节点的若干质体，使系统自由度数减少，系统的质量和刚度矩阵可直接通过结构的离散化得出；因此，把带传动和谐波减速器传动机构等效为线性无质量弹簧[9-10]，简化整个机械臂结构系统阻尼为线性比例，关节臂之间的阻尼简化为小阻尼。

完成上述假设后，整个机器人机械臂可简化为图1(b)所示的刚柔耦合模型。

1.2 振动特性分析

机械臂结构振动特性与系统本体固有频率密切相关，机械臂本体固有频率与外载荷无关，且阻尼对固有频率影响可以忽略，根据模态分析理论，机器人动力学模型可以用下式表示[11-13]：

(1)

式中：M—质量矩阵；K—系统刚度矩阵；Q—位移向量。

将式(1)进行求解，可以得到系统的特征方程为：

(2)

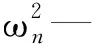
因此，为了计算系统的固有频率，需要获得模型的各物理量的参数值，根据图1的简化模型，笔者给出主要的关节的两种工作姿态的物理参数定义，如表1所示。

表1 机械臂主要物理参数特征值

利用MATLAB在矩阵运算方面的强大运算能力，笔者应用式(2)及表1的物理参数，对简化模型的系统进行仿真分析，获得机械臂本体不同姿态固有频率，如图2所示。

图2 机械臂本体不同姿态固有频率

由图2可知，其一阶固有频率在15 Hz附近，二阶固有频率集中在30 Hz附近。

2 实验测试过程

2.1 测试方案

在工作过程中，工业机器人机械臂通过各个关节臂柔性连接之间坐标系旋转变换来完成末端工作轨迹操作，机械臂在进行作业时，柔性部件如谐波减速器和轴之间传动，再传到皮带轮。整个过程引起机械臂执行机构、6个关节间产生一定的弹性变形[15]，这样振动也就不可避免，机械臂等效杆件间的振动最后会累积传递到末端工作执行器上，导致机械臂末端执行机构不能准确地完成指定轨迹作业，使得微调过程时间增加，最终使结构动作响应不灵敏。

因此，为了获得系统振动原因，需要测试出单体振动频率和本体固有频率，结合振动系统的振动传递特性，可以把振动传递模型看成激励源—振动传递的路径—接受体的传递过程模型[16-17]。

其中，振动的传递是指激励源的振动，由不同路径通过结构传递到接受体的过程，因此，根据机器人机械臂运行的特点和工作状态，机械臂结构振动传递过程如图3所示。

图3 机械臂振动传递过程

根据机械臂结构运动特性和测试要求，笔者确定本体振动测试激励方式、传感器布点位置及测试状态。由于机械臂本体结构复杂，多关节传动与机电耦合等因素会影响系统动态特性[18]。

为了保证测试实验的有效性，笔者选取机械臂的两个最可能出现振动超标的姿态作为测试工况：姿态1为一轴大臂垂直向上与轴二连接关节小臂成90°；姿态2为大臂与小臂成180°。选取2个激励点(结构初始段一轴和二轴关节处，结构二轴和三轴关节处)和4个拾振点(4，5，6和末端执行件上各放一个振动加速度传感器)，在敲击测试中，每个点激振3次，取3次实验数据进行后处理。

测试结构过程原理如图4所示。

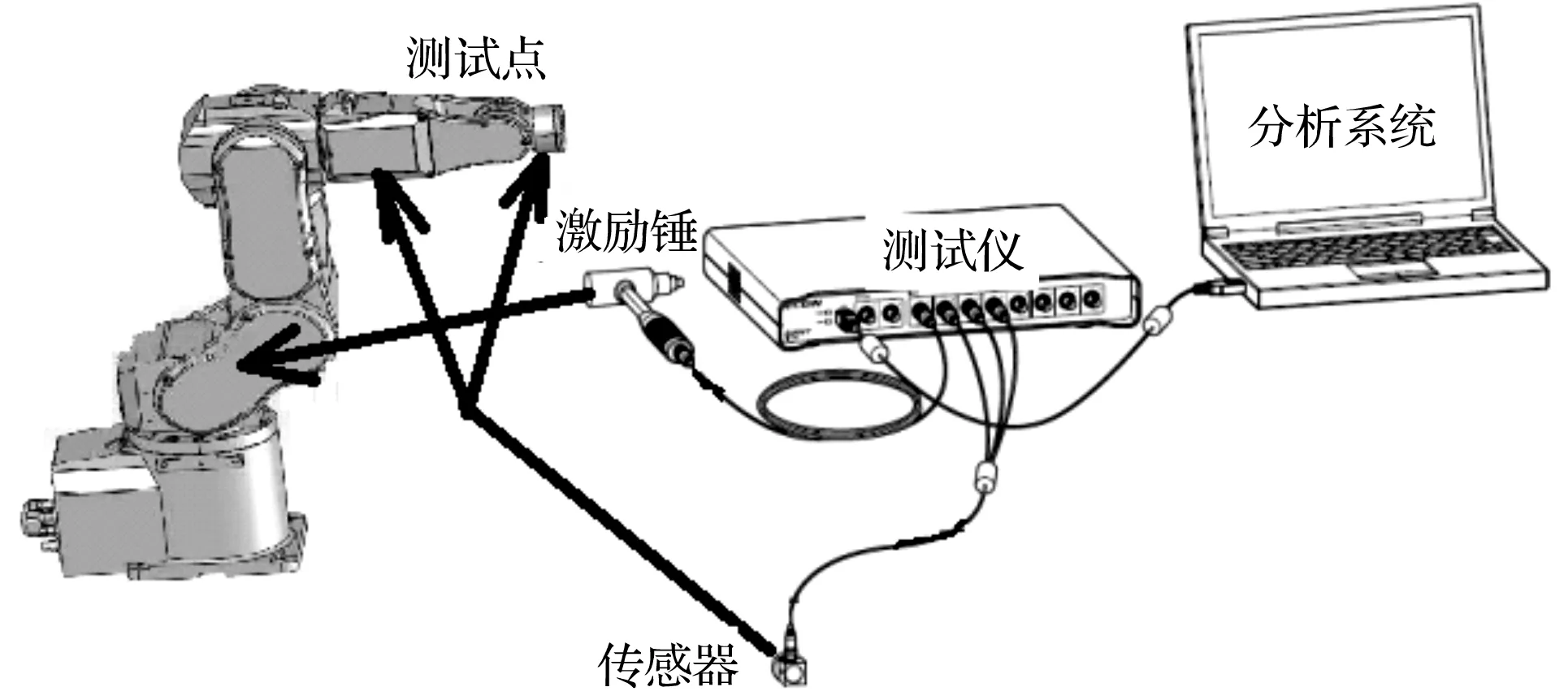
图4 振动测试过程

2.2 本体振动模态测试

按照上述测试方案，机器人机械臂以设定的工作姿态的位置静止时，利用力锤敲击测试获取其机器人本体的频响函数。

机械臂X，Z向频率响应测试结果如图5所示。

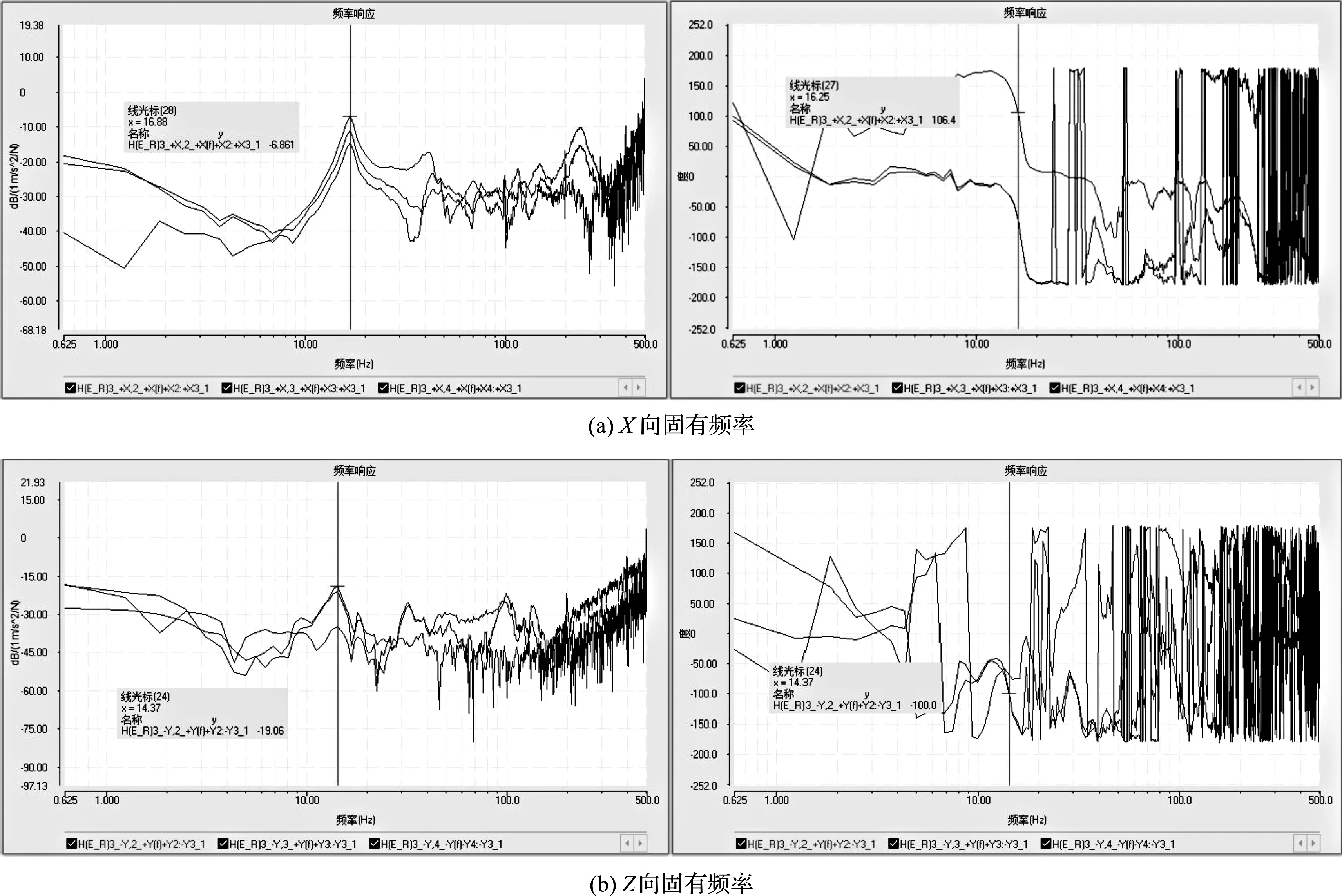
图5 机械臂X，Z向频率响应图

由图5(a)可获得，机器人机械臂本体在设定位置姿态的X向一阶固有频率为18.25 Hz，二阶固有频率为38 Hz；

由图5(b)可获得，Z向一阶固有频率为18.05 Hz，二阶固有频率为34.26 Hz。

2.3 单体振动模态测试

根据机械臂结构和使用特点，动力传动和能量消耗主要是前三轴，振动源也主要来自这三轴。

为了减少测试工作量，笔者只对前三轴工作运行激励下测试末端振动情况，获得一、二、三轴单独运转激励下末端件的振动，如图6所示。

从图6(a)可知：一轴单轴启动和停止瞬间抖动相对剧烈，抖动范围达到±0.6 G，平稳运行时抖动范围在±0.1 G；选取单程运行分析，运行中机器人末端抖动，结合启动和停止时末端的晃动数据，在0.7 Hz～45 Hz频率范围抖动频率较为复杂，抖动频率主要分布在1.25 Hz～9.94 Hz之间；

从图6(b)可知:二轴单轴启动和停止瞬间抖动相对剧烈，抖动范围达到±0.6 G，而平稳运行时抖动也较大，抖动范围在±0.4 G；选取单程运行分析，运行中机器人末端抖动，结合启动和停止时末端的晃动数据，抖动频率主要分布在12.37 Hz～18.85 Hz之间；

图6 一、二、三轴单独运转激励下末端件的振动

从图6(c)可知：三轴单轴抖动范围主要在±0.15 G；选取单程运行分析，运行中机器人末端抖动主要在9.84 Hz。

3 测试结果分析

综合以上数据，仿真所获得固有频率和实验测试的数据比较接近，说明测试方案可行性；且前二阶固有频率都介于10 Hz～40 Hz之间，但前二阶固有频率都较低，这说明结构的整体强度较低，需要通过结构的改进或材料强度的增加，来提高结构的低阶固有频率。

由于机械臂在运行过程中四轴没有转动，五轴和六轴转速较低，可以排除四、五、六轴对工作状态运行中机器人末端抖动的影响。

机械臂在运动过程中，监测到一、二、三轴单关节运动的电机转速分别为163 r/min、257 r/min、600 r/min。根据机器人关节安装特点，一轴主要影响z向的抖动，并且转速过低，排除一轴激励对机器人末端X向和Z向的影响。

通过测试二、三轴单轴运动抖动数据显示：图6(a～c)中横轴表示抖动频率，纵轴表示振动加速度，二轴电机以257 r/min单轴运动时，抖动表现为±0.6 G范围波动，主要频率在12.37 Hz～18.85 Hz之间；三轴电机以100 r/min单轴运动时，抖动表现为±0.1 G范围波动，主要频率为9.84 Hz。

测试结果显示，二轴单轴以600 r/min运动时的主要振动频率与工作状态下运动时的末端抖动频率接近。因此，可以推测机器人工作中的末端抖动的主要影响因素是由于二轴运动过程的振动引起。

4 结束语

针对某新型机器人末端执行件工作当中出现严重抖动问题，笔者构建了一种激励+单体+本体+末端振动的路径传递模型，提出了一种机器人本体固有频率测试和单轴工作模式振动测试相结合的模态试验方法，该方法有效地推测出了机器人过激抖动的原因，验证了测试方案的可行性。结论如下：

(1)通过对本体进行锤击激励响应测试，获取系统固有频率，可有效地找到结构共振频率区域，并且发现本体一、二阶固有频率相对较低，需要改进机器人本体刚度和强度来提高低阶本体固有频率；

(2)二轴转速在600 r/min时末端振动频率与本体振动固有频率接近，推测为二轴运动造成末端振动过激的原因，可以通过优化二轴的结构、更换二轴电机或者更换谐波齿轮来改善机械臂振动；

(3)通过对仿真分析和试验模态分析结果的对比，可以看出两种方法的本体模态分析的结果存在微弱差异，这主要是对结构进行模态仿真计算时需要对模型进行简化，从而达到在误差允许范围内尽量减少计算量的目的。因此，分析的结果势必与实际结果存在误差，而通过实验的方法，对本体进行模态分析的误差则主要来源于实验员的误操作、节点的选择或者电机的振动的微弱影响。

笔者在研究各关节单体运动对末端执行机构的抖动影响时，忽略了各关节耦合作用对结构的影响，研究过程存在一定的片面性，因此，今后将以此作为进一步研究的方向。