基于MATLAB的微轴承动力学特性的数值分析*
兰正义,伍 林*,吕刚磊
(1.上海应用技术大学 机械工程学院,上海 201418;2.郑州科技学院 机械工程学院,河南 郑州 450064)
0 引 言
目前,微机电系统下微轴承—转子系统稳定性的判断分析,主要是结合微轴承的动力学特性系数进行分析而获得,但大部分的动力学特性参数计算是在基于不考虑气体滑移的连续模型下获得的[1-2]。
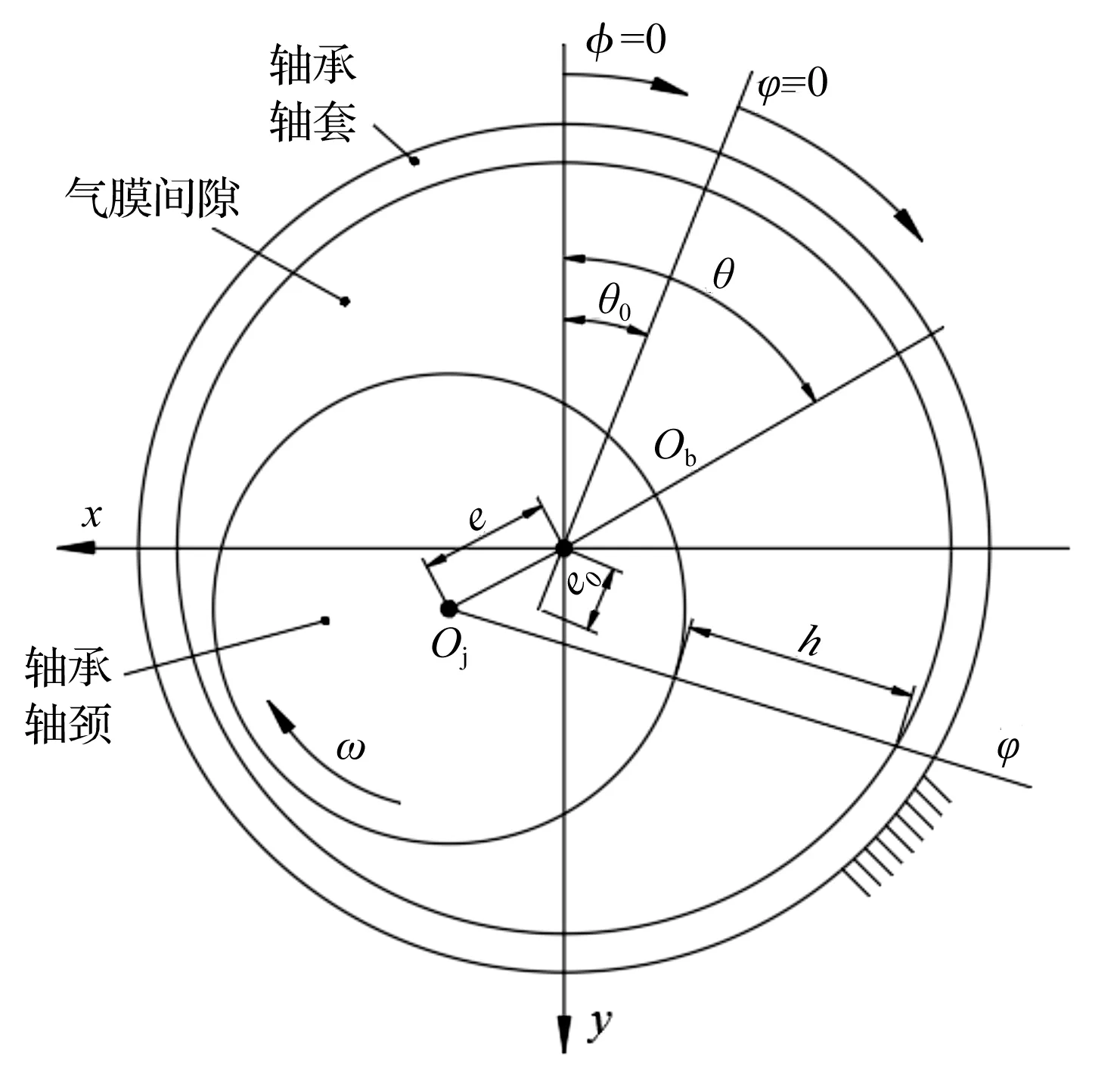
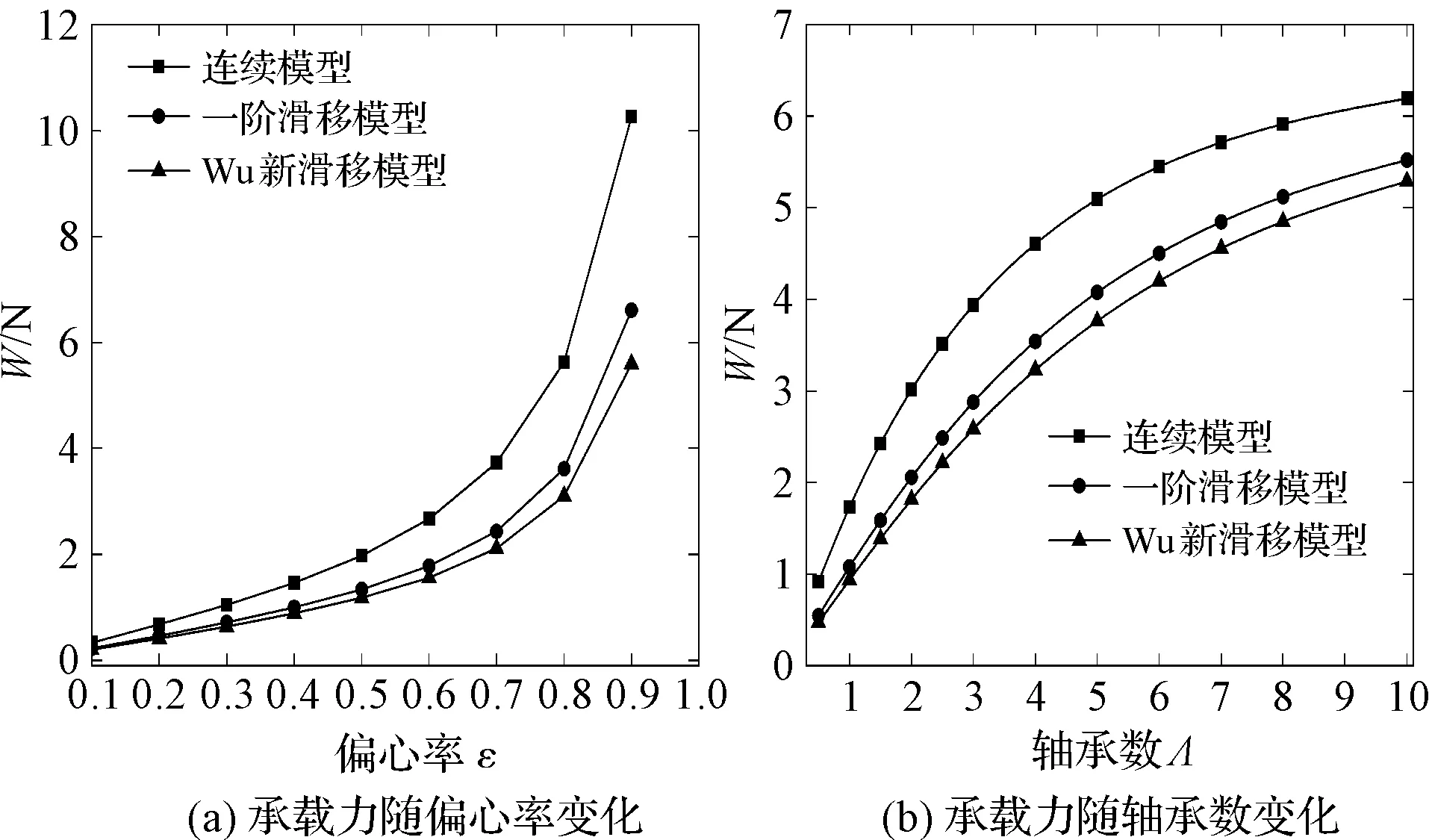
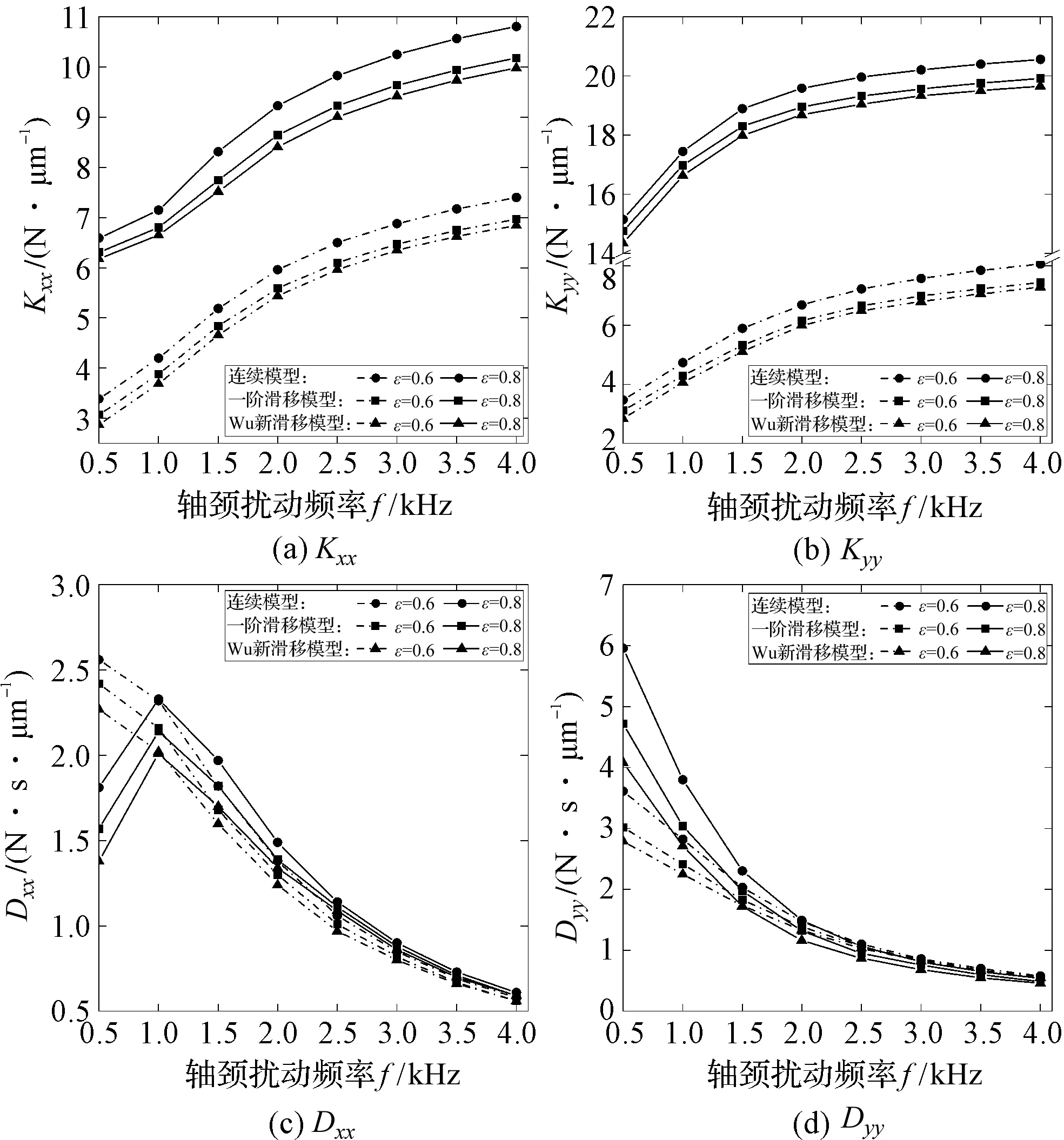
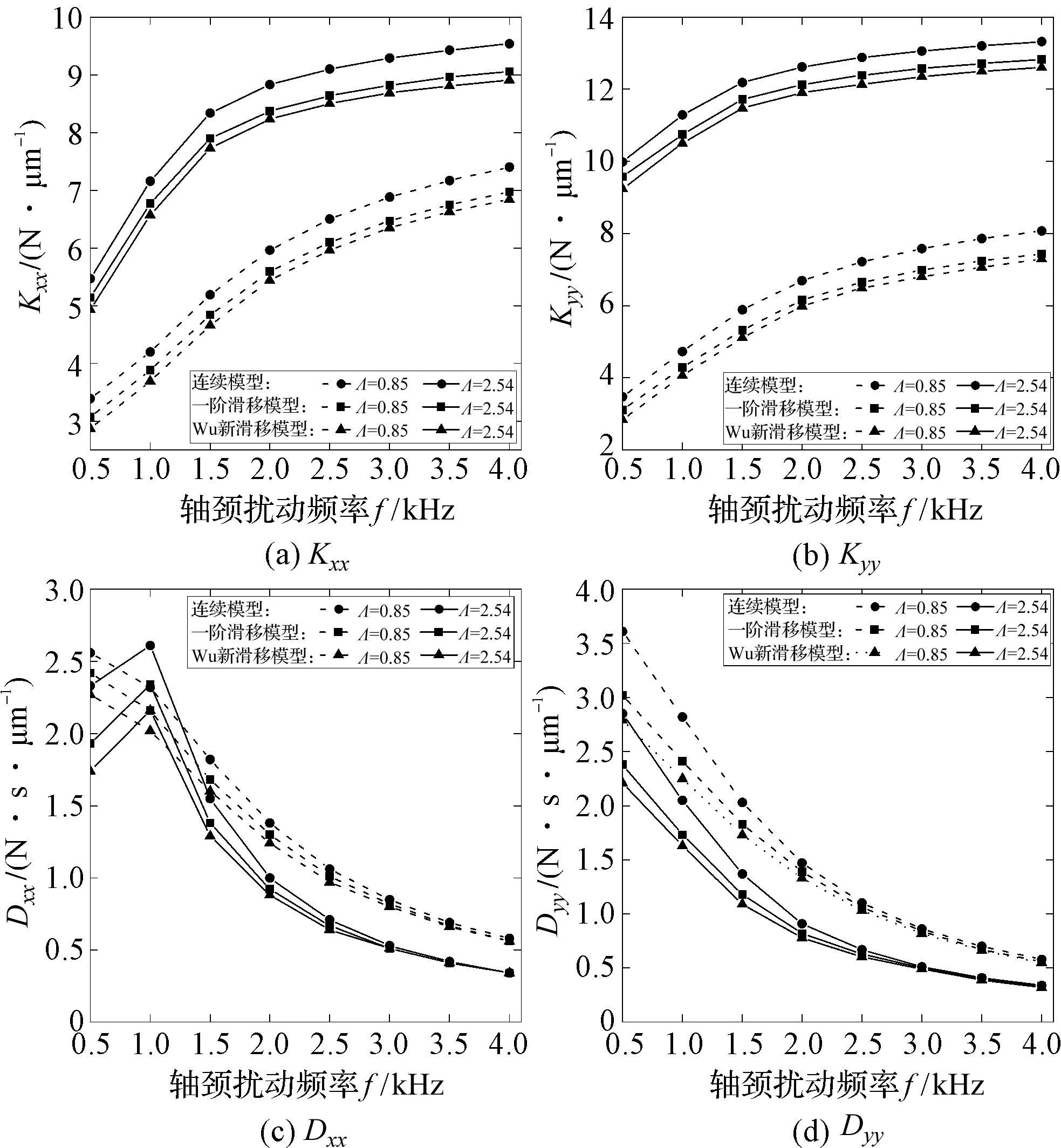
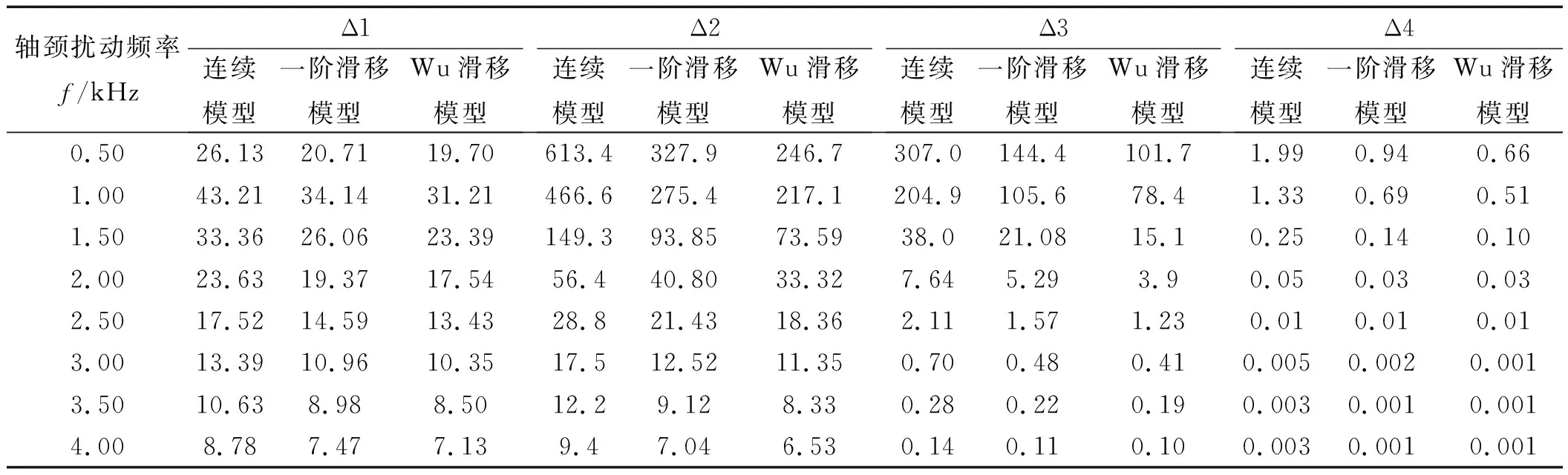
然而随着微机电系统尺寸的不断微型化,其关键支撑部件轴承间的润滑气膜将会变得极薄,气体将会处于稀薄状态,其间的气体将会在固壁表面发生滑移,此时若采用不考虑滑移影响的传统连续模型分析轴承转子系统的动力学特性,将影响其准确性。因此,需考虑滑移效应下提出的修正模型对其进行动力学特性分析[3-4]。文献[5]指出了当轴承最小气膜间隙处的克努森数Kn值处于气流过渡流动区域(0.1 针对以上问题,以MEMS下的微轴承为研究对象,本文推导考虑一阶滑移修正及Wu新滑移修正的动力学雷诺方程,采用MATLAB编程软件编制不同模型下用于数值计算动力学雷诺方程的程序,比较不同轴承数、偏心率、轴颈扰动频率下连续模型、一阶滑移模型和Wu新滑移模型的动力学特性系数,进而分析研究气体滑移对微轴承动力学特性的影响规律;在此数值计算基础上,对比分析微轴承刚性转子系统在连续模型、一阶滑移模型和Wu新滑移模型下的稳定性。 微动压气体轴承,依靠轴承与轴套之间充入的黏性气体,形成楔形间隙而发生相对运动,从而自动产生气膜压力,实现轴承转子的动压悬浮。 微轴承动压作用示意图如图1所示。 图1 微轴承动压作用示意图ω—角速度;e—偏心距;h—轴承间隙 在定常、等温条件下,传统连续、一阶滑移及Wu新滑移修正模型下的润滑Reynolds方程的无量纲形式为: (1) 为方便计算,笔者将3种模型的系数做归纳处理。 模型系数如表1所示。 表1 模型系数 Kn0—参考克努森数,Kn0=C1/ph=C1/(pahmPH);C1—最小气膜间隙,C1=6.8×10-3;α—协调系数;f—取值函数,f=min[1/Kn0,1] 结合式(1)、表1可得到在小扰动工况下修正的静态雷诺方程,及关于PE和PΘ的修正偏微分动态雷诺方程。 修正的静态雷诺方程为: (2) 静态气膜厚度为: H0=1+εcosφ (3) 无量纲静态求解边界条件为: (4) 关于PE修正后的动态雷诺方程为: (5) 相应的动态气膜厚度为: HE=cosφ (6) 相应的无量纲边界条件为: (7) 关于PΘ修正后的动态雷诺方程为: (8) 相应的动态气膜厚度为: HΘ=sinφ (9) 相应的无量纲边界条件为: PΘ(φ,±B/2)=0 (10) 1.3.1 静态承载力、偏位角求解表达式 联立式(2~4),基于MATLAB编制静态雷诺方程有限差分程序,迭代求解可得到静态气膜压力P0分布的数值解,从而得到轴承静态承载力W和轴颈偏位角θ的求解表达式,即: (11) (12) 式中:Wn—轴颈承载力在偏心方向的分量;Wt—轴颈承载力在垂直偏心方向的分量。 1.3.2 动态刚度系数和动态阻尼系数求解表达式 根据式(5~10),基于MATLAB编制动态雷诺方程有限差分程序,通过迭代求解可得到微轴承的动态气膜压力PE和PΘ,从而可以得到滑移效应下,微轴承的动特性系数求解表达式: (13) 转换式(13)中的系数代入到直角坐标系中,可求解直角坐标系下的动特性系数,即: (14) 结合文献[8]可知,该系统的力平衡运动方程为: (15) (16) 将上述微分方程组合并,则该方程组的通解为: (x,y)=(x0,y0)est (17) 式中:s—为复频率,s=u+iwj;u—复数的实部(阻尼);ωj—虚部(轴颈自然涡动频率)。 联立式(15~17),整理可得: (18) 由线性代数理论可知,式(18)有非零解的充要条件是该方程组的系数行列式为0,即: (19) 展开式(19)的2阶行列式,可得到微轴承—刚性转子系统的特征方程式: a4s4+a3s3+a2s2+a1s+a0=0 (20) (21) 根据系统稳定性Routh-Hurwitz判别准则[9]可知,只需要判断特征值s的解是否都有负实数部,就可以判断轴承转子系统是否稳定。因此,通过计算式(20)中的特征值,就可预估微轴承刚性转子系统的稳定性。 针对如图1所示的微轴承结构,微轴承设定最终微小间隙下气膜收敛精度为10-6。 数值仿真计算参数如表2所示。 表2 数值仿真计算参数 为进行微轴承动力学特性的数值分析[10],本文采用MATALB编程平台编制程序,进行微轴承动力学特性的数值分析。 数值仿真流程图如图2所示。 图2 数值仿真流程图 为验证本文用于微轴承动力学特性分析时程序的正确性,基于如图2所示的数值仿真流程图,笔者采用有限差分法进行数值计算,并将得到的结果与文献[11]的数值结果进行对比。 数值仿真程序验证图如图3所示。 图3 数值仿真程序验证图 对比结果表明:本文程序得到的动特性系数与文献中的数据几乎完全一样;使用该程序计算得到的动力学特性系数与文献中的数据相对误差均在3%以内,由此验证了本文程序的准确性。 为分析微轴承的静态特性,笔者从微轴承静态雷诺方程出发,对比分析最小膜厚度处微轴承在3种模型下的静态气膜压力分布及轴承数(描述气体可压缩性对动压效应影响程度的一个压缩系数,标量)、偏心率(描述轴颈运转时的偏心程度,标量)分别对轴承的静态承载力、偏位角的影响规律。 基于如表2所示的轴承结构参数,在φ=180°、偏心率0.6及轴承数为1.7时,3种模型下的气膜压力分布图如图4所示。 图4 3种模型下的气膜压力分布图 对比3种模型下的气膜压力分布发现:在最小气膜厚度处,3种模型得到的气膜压力差异明显,这是因为在最小气膜厚度处,和气体滑移效应密切相关的流体粘性剪切应力最强,致使在该区域的气流速度分布发生变化,进而使该区域的气压分布发生变化;同时,可以得到连续模型预测的气膜压力最高,一阶滑移模型次之,Wu新滑移模型预测的气膜压力最低。 为进一步分析微轴承的静态特性,笔者采用数值分析方法,得到3种模型下承载力与偏心率、轴承数之间的关系,如图5所示。 图5 3种模型下承载力与偏心率、轴承数之间的关系 从图5可以看出:在相同条件下,考虑气体滑移影响时,随着偏心率、轴承数的变化,气体滑移影响下的承载力明显下降,相比滑移模型预测的结果而言,连续模型预测的承载力偏大;且随着偏心率、轴承数的增大,各模型之间的承载力偏差在逐渐变大,这是因为偏心率和轴承数的增大,直接导致了最小气膜处的间隙变大,剪切应力增强,气体滑移效应变得显著,进而使最小气膜间隙处的气膜压力降低,轴承的承载力下降。但连续模型并没有考虑气体滑移的影响,所以预测得到的承载力值相对较高。 综合上述的分析可知,连续模型预测的承载力偏差最大、一阶滑移模型次之、Wu新滑移模型最小;对比一阶滑移模型和Wu新滑移模型预测的轴承气膜压力可知,一阶滑移模型较高地预估了滑移效应下轴承的承载力。 因此,在对滑移下微轴承的动力学特性分析时,需考虑精度更高的Wu新滑移模型。 为分析气体滑移对微轴承动态特性的影响,笔者按表2所示的轴承结构参数(气膜收敛精度为10-6),从微轴承动态雷诺方程出发,研究了气体滑移影响下轴颈扰动频率、偏心率、轴承数与轴承动态刚度和动态阻尼系数的变化关系。 3种模型下,动态特性系数与偏心率之间的关系如图6所示。 图6 3种模型下动态特性系数与偏心率之间的关系 从图6中可以看出: (1)在相同条件下,考虑气体滑移的影响时,轴承的动态刚度系数,受偏心率的影响较大,轴承的动态阻尼系数,几乎不受偏心率的影响;其中,当轴颈的扰动频率大于2.5时,动态主阻尼系数几乎不受偏心率的影响; (2)在相同轴颈扰动频率下,大偏心率对应着大的动态主刚度系数和主阻尼系数,且由于只有垂直方向受外力作用,垂直方向上大偏心率对应的动态主刚度系数Kyy、主阻尼系数Dyy相对小偏心率较大。 基于静特性数值分析计算结果,3种模型下动态特性系数与轴承数之间的关系如图7所示。 图7 3种模型下动态特性系数与轴承数之间的关系 从图7中可以看出:在相同条件下,考虑气体滑移影响时,不同轴承数下的动态主刚度系数Kxx、Kyy均随轴颈扰动频率的增大而增大,主阻尼系数Dxx、Dyy随轴颈扰动频率的增大而减小,且气体滑移对阻尼系数的影响也在逐渐减弱;大的轴承数对应着大的动态主刚度系数、小的动态主阻尼系数,这主要是因为,大转速意味着高气膜压力,会使相对应的轴承轴颈位置发生变化,轴承的动态主刚度随着转速的增加而变大,相对应的动态主阻尼系数随之变小。 由图(6,7)可知,在气体滑移影响下,不同轴承数、偏心率对应的动特性系数均有所下降,且Wu新滑移模型计算的值远低于连续模型和一阶滑移模型,这主要是因为气体滑移会使润滑气体的速度有所降低,进而气膜压力降低,从而导致轴承动特性系数减小。 在偏心率为0.6、轴承数为1.7时,结合3种模型下的动特性系数与轴承转子系统稳定性判别理论,可求得各扰动频率下特征值对应的所有子行列式的值,判断在该扰动频率下是否满足稳定性条件,为轴承稳定性设计提供理论依据。 在相应扰动频率下,3种模型各子阶行列式的值如表3所示。 表3 在相应扰动频率下3种模型各子阶行列式的值 从表3可知,3种模型在各扰动频率下的各子行列式的值都为正数,且Wu新滑移模型计算的值相比连续模型、一阶滑移模型低;即在轴承数为1.7的情况下,微轴承刚性转子在相应扰动频率范围内是稳定的,且连续模型较高地估计了转子系统的稳定性。 针对微机电系统下传统连续模型无法准确描述气体滑移对微轴承动力学特性影响规律的问题,笔者推导了考虑一阶滑移修正及Wu新滑移修正的动力学雷诺方程,比较了不同轴承数、偏心率、轴颈扰动频率下连续模型、一阶滑移模型和Wu新滑移模型的动力学特性系数,进而研究了气体滑移对微轴承动力学特性的影响规律;在此数值计算基础上,笔者对比分析了微轴承刚性转子系统在连续模型、一阶滑移模型和Wu新滑移模型下的稳定性。 研究结果可知,气体滑移下轴承的动力学特性与轴承的轴承数、偏心率及轴颈扰动频率密切相关,在微小气膜间隙、高转速工况下,不考虑气体滑移影响的连续模型较高地估计了轴承刚性转子系统的稳定性,且Wu滑移模型下得到的值最小。 综上所述,结合物理理论依据和微小间隙下气体滑移的影响,在设计微机电系统下的微轴承时,为得到气体滑移下更准确的轴承设计参数,应使用Wu新滑移模型对传统连续模型下的动力学雷诺方程进行滑移修正。 为计算方便,笔者使用的MEMS下的微轴承结构较为简单。在今后的研究中,笔者将会引入更复杂的微轴承结构,来验证分析该理论的适用性;同时,考虑使用数值仿真与试验相结合的方法,笔者在不同的算例条件下,分析气体滑移对微轴承动力学特性的影响,为设计更优的MEMS下微轴承提供帮助。1 滑移修正下的动力学方程
1.1 微轴承的滑移修正雷诺方程
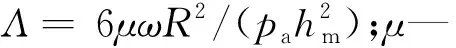

1.2 滑移修正下的静、动态雷诺方程
1.3 动力学特性系数求解表达式
2 微轴承转子系统稳定分析方法
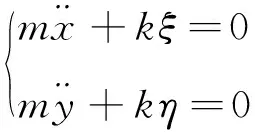
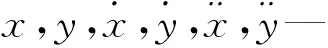
3 数值仿真实验及结果分析
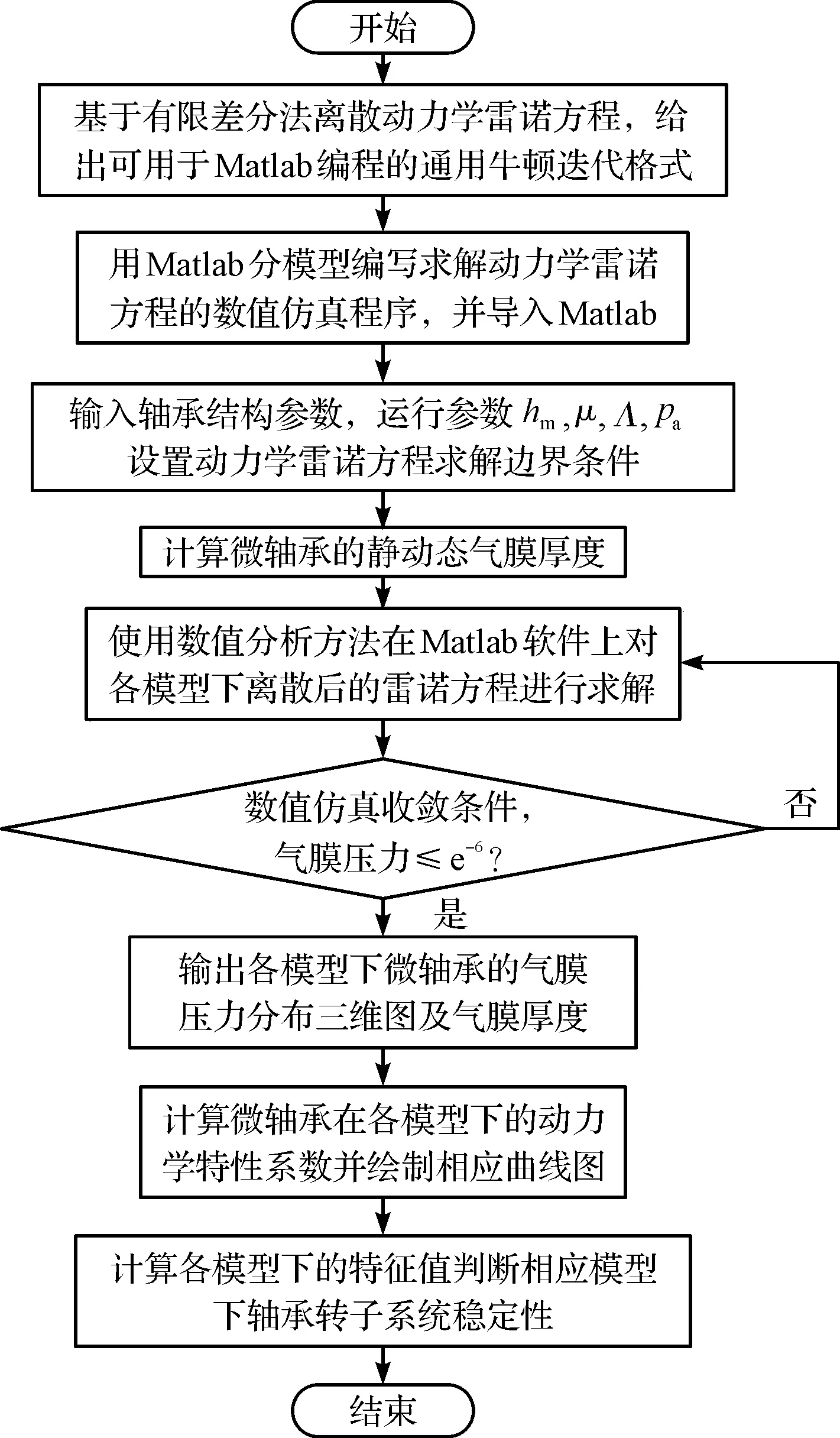
3.1 数值仿真程序验证
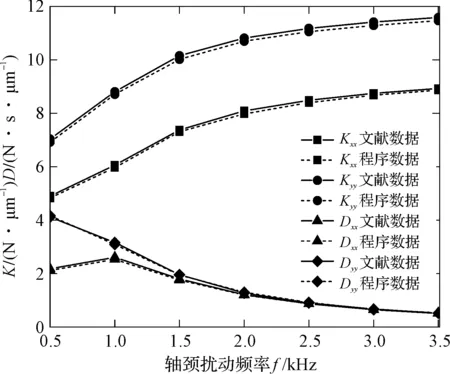
3.2 静特性系数数值仿真结果分析
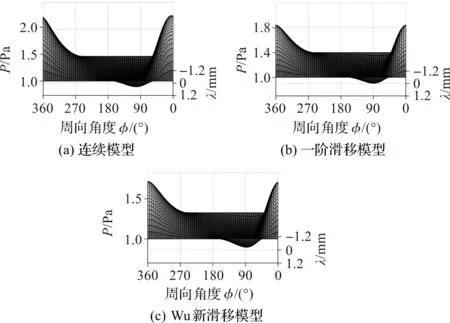
3.3 动态特性系数数值仿真结果分析
4 微轴承转子系统稳定性分析
5 结束语

