高精度挤出橡胶在线定重分剪机设计与启停抑振控制研究*

王嘉恩，聂晓根

(福州大学 机械工程及自动化学院，福建 福州 350108)

0 引 言

橡胶是一种具有可逆形变的高弹性聚合物材料，具有电绝缘性、耐磨性等优良特性，被广泛运用于各种密封场合[1-2]。橡胶密封件虽小，但对工作系统的性能影响重大，所以对橡胶密封件的原料及其加工质量都有较高的要求。当前，橡胶密封件生产工艺流程主要包括：塑炼、混炼、成型、硫化等[3]。在压铸型之前，需要对经过炼胶后的挤出橡胶进行高精度称重和分剪。企业现有的挤出橡胶称重和分剪通常由人工手动操作完成，分剪过程往往需要多次反复的称量和剪切才能达到称量精度要求，生产效率低下，操作者劳动强度大。

在橡胶定重分剪研发方面，陈耿[4]研制了X、Y轴龙门式橡胶裁剪机，该设备刀具由单个刀片构成，并由曲柄滑块机构驱动；邓肖粤等[5]在橡胶轮胎生产线上使用PLC作为控制器，设计了一把由电机旋转带动的切刀；张国文等[6]发明了一种橡胶冲切装置，在橡胶定位完成后，利用液压杆冲压下料，然后进入收料仓收集。以上均是对块状或片状橡胶进行定重分剪，尚未见对挤出橡胶的高精度动态定重分剪的研究报道。

笔者针对现有精密橡胶制品高精度备料要求，以提高橡胶制品备料精度、生产效率、降低操作人员劳动强度和成本为目标，对挤出橡胶在线自动定重分剪一体化设备进行研究。

1 分剪机结构设计

橡胶定重分剪备料加工需要配合现有的橡胶挤出机实现。加工时橡胶挤出机将橡胶原料源源不断地从出料口挤出，形成一条连续运动的橡胶条，挤出橡胶经称量系统定重称量；向控制器PLC发出指令，控制分剪机快速响应进行橡胶条分剪。

为尽可能减少称量系统自身重量对称量精度的影响，称重传感器采用电阻应变片式传感器悬臂布置，该称量系统可与分剪机构分离，避免分剪动作产生的冲击对称量精度造成影响。

悬臂式称量系统结构如图1所示。

图1 悬臂式称量系统结构示意图

在挤出橡胶在线定重分剪加工中，分剪机的响应对系统的称量精度具有重要影响。一方面为了高速高精度分剪橡胶条，要求分剪机应高速响应完成分剪动作；另一方面为了实现高精度称量，要求分剪机高速运行时振动应小。因此，分剪机的结构设计和运动控制对一体机性能具有决定性影响。其中，刀具设计需要综合考虑以下因素：

(1)刀片同步性的保持。执行分剪动作时，两刀片应能以大小相同、方向相反的角速度进行旋转运动。若两刀片旋转的角速度大小无法严格保持一致，则分剪位置将会出现偏离，导致分剪位置偏差，产生剪切冲击，并产生误差；

(2)刀片间距的保持。刀具的剪切力必须能使橡胶条迅速分剪且切口平整。而剪切力除了受电机转矩及传动系统影响外，还受两刀片剪切面间距的影响。若间距过大，则无法进行剪切；若间距过小，则两刀片间接触面配合较紧易造成“卡刀”；

(3)刀片长度的要求。刀片的剪切力来源于电机输出轴，当电机输出转矩一定时，刀片对橡胶条的作用点与刀片转动中心距离越小，则剪切力越大。同时，需考虑分剪机的空间位置限制，刀片应有一定的长度才能保证在剪切橡胶条时不与分剪机产生干涉；

(4)刀片的厚度要求。执行分剪动作时，刀片厚度越薄就越锋利，越容易剪断橡胶条，但过薄的刀片其抗扭强度也相对不足。同时，过薄的刀片也不利于刀片在旋转轴上的轴向定位和周向定位。

为了实现分剪运动，分剪机两刀片需作同轴反向等角度往返回转运动，为此，笔者设计了专用的橡胶分剪机，如图2所示。

图2 同轴双向式分剪机结构旋转剖面图1-电机；2-联轴器；3-主轴；4-胀紧套；5-主动齿轮；6-从动齿轮；7-套杯；8-下刀片；9-上刀片；10-一级从动轴；11-一级惰轮；12-二级从动轴；13-二级惰轮

该分剪机由两条传动链组成，电机通过联轴器和主动轴直连，主动轴另一端通过平键和上刀片固连，再由锁紧螺母固定，构成主传动链。次传动链中，主动轴经过其轴上的齿轮与一级从动轴上的一级惰轮啮合；然后，一级惰轮再与二级从动轴上的二级惰轮啮合，经过二级传动，该从动轴的旋转方向和主动轴的转向一致；再将该二级惰轮与主动轴上的另一齿轮啮合，达到将与主动轴相反方向的旋转运动传回主动轴的目的；最后，将该齿轮和套杯固连，套杯和下刀片固连，构成次传动链。同时，为实现往复分剪，笔者将刀片设计成双侧刀刃结构。

因为齿轮间的啮合传动比均为1∶1，两刀片的同步性在机械结构上得到了保证。同时，刀片间距的保持采用了具有一定弹性模量的弹簧自动进行动态调整。在安装剪切机时，为了可以无级调节两刀片，在合并剪切时，刀片刀尖方向位于橡胶条挤出方向上，这里设计通过胀紧套锁紧方式固定主动轴上的齿轮。

分剪机三维效果如图3所示。

图3 同轴反向式分剪机三维效果图

2 分剪动作分析

执行分剪动作时，需要精确控制刀具刀片的位置，即需要对步进电机的角位移进行定位控制。同时，为避免分剪过程中产生的机械振动对称重系统的影响，减少机械柔性冲击，需要对步进电机的启停作加减速控制。

根据橡胶高精度分剪要求，笔者对电机的运动控制采用三段控制方法：第一阶段为电机开始转动到刀刃刚接触到橡胶条；第二阶段为刀刃切入橡胶条到橡胶条被完全剪断；第三阶段为刀片分剪完成并继续旋转至反向零点位置。

由于热熔融状态下的橡胶具有很大的黏度，与刀片之间存在较大的摩擦力，橡胶条与刀片之间的相对滑移可忽略不计。

分剪动作第一阶段与橡胶条实验抽象成的几何模型如图4所示。

图4 分剪动作第一阶段示意图

图4中，电机开始转动到刀刃刚接触到橡胶条，这个阶段可看作是电机的空载运行，用于电机的加速运动。

图4中，虚线标识为初始位置，实线标识为目标位置，两位置间步进电机转过了α角度，即：

α=λ-δ

(1)

式中：λ—在刀片的初始位置时刀片中心线与橡胶条的挤出平面夹角；δ—在刀刃刚接触到橡胶条时刀片中心线与橡胶条的挤出平面夹角。

要求α，需对夹角δ进行求解。为方便推导计算，将刀具剪切橡胶条实验抽象成几何模型。

其中：圆A为橡胶条横截面，点O为刀具旋转中心，点B为刀刃与橡胶条接触点，点C为刀尖点。

已知橡胶条横截面中心与刀具旋转中心距离OA、刀具长度OC、橡胶条横截面半径R和半个刀尖角θ的值，求δ的值。作辅助线，过点A作AB⊥CM于点B。

在△MOC中，由正弦定理得：

(2)

其中：

(3)

sin∠CMO=sin(π-(θ+δ))=sin(θ+δ)

(4)

将式(3，4)代入式(2)中，得：

(5)

所以，可得到：

(6)

将式(6)代入式(1)中，可以求出步进电机第一阶段转过的角度α为：

(7)

分剪动作第二阶段与其几何模型如图5所示。

图5 分剪动作第二阶段示意图

图5中，刀刃切入橡胶条到橡胶条被完全剪断，这个阶段电机对外做功，用于电机的匀速转动。

两位置间步进电机转过了β角度，即：

β=δ-ε

(8)

式中：δ—在刀刃刚接触到橡胶条时刀片中心线与橡胶条的挤出平面夹角；ε—在刀刃完全剪断橡胶条时刀片中心线与橡胶条的挤出平面夹角。

同理，要求β，需对夹角ε进行求解。

其中，点N为刀刃完全剪断橡胶条时，刀刃与橡胶条的交点。已知橡胶条横截面中心与刀具旋转中心距离OA、刀具长度OC、橡胶条横截面半径R和半个刀尖角θ的值，求ε的值。

在△NOC中，由正弦定理得：

(9)

其中：

ON=OA+R

(10)

sin∠CNO=sin(π-(θ+ε))=sin(θ+ε)

(11)

将式(10，11)代入式(9)中，得：

(12)

所以，得到：

(13)

将式(13)代入式(8)中，可以求出步进电机第二阶段转过的角度β为：

(14)

在第三阶段，刀片剪切完成并继续旋转至反向零点位置，为下一个工作循环做准备。

分剪动作第三阶段如图6所示。

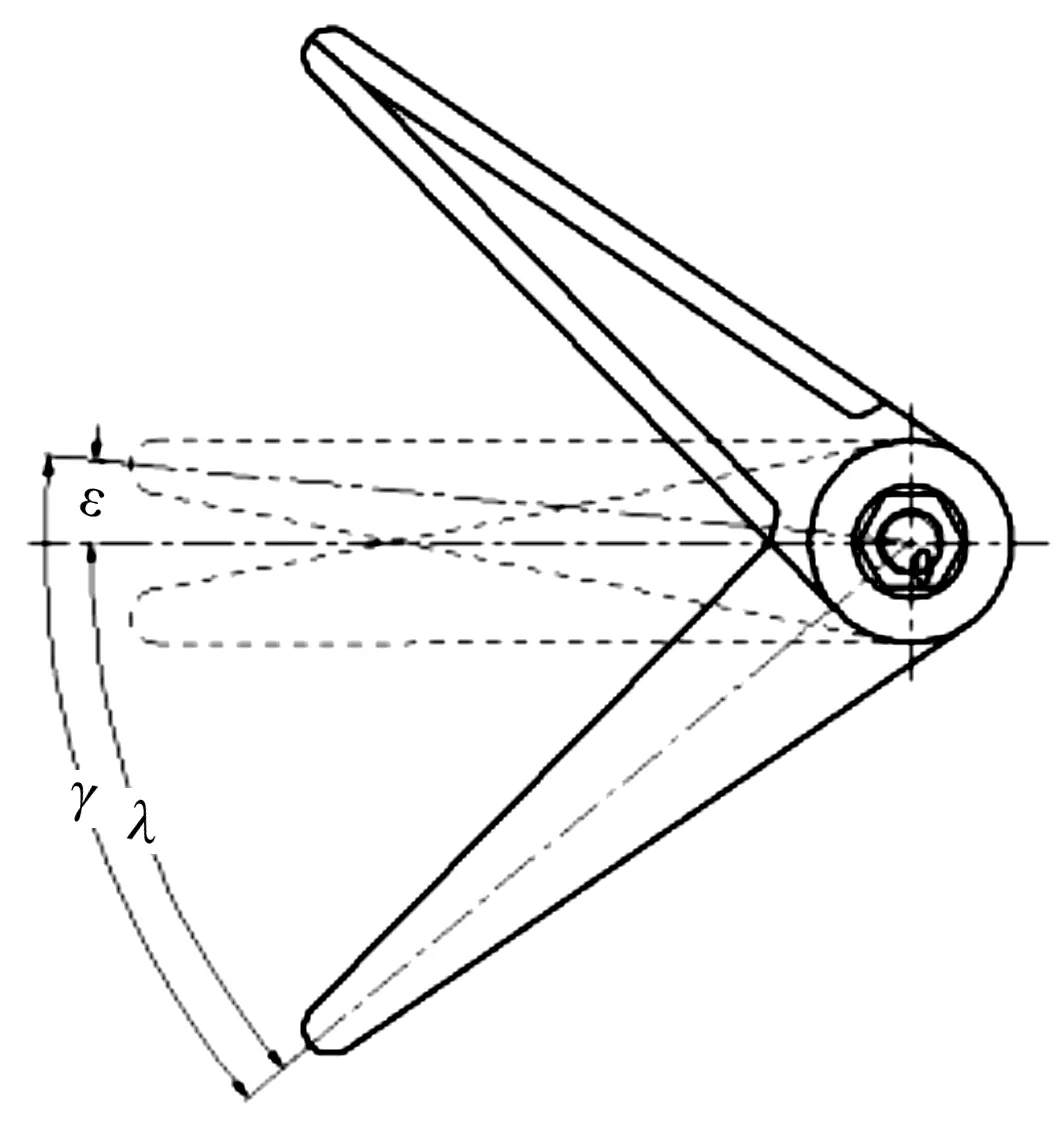
图6 分剪动作第三阶段示意图

从而可以求出步进电机第三阶段转过的角度γ为：

γ=λ+ε

(15)

(16)

3 加减速算法

PLC自带加减速功能的脉冲输出指令PLSR，在确定最大转速、位移和加减速时间后，可以直接输出加减速脉冲信号。但是，其速度变化为一次函数，加速度在启停时会发生突变，对系统产生了较大的振动。

PLC加减速脉冲输出如图7所示。

图7 PLC加减速脉冲输出图

所以，为减少步进电机启停时的机械振动对称重系统的影响，需要对电机进行加减速控制。在电机控制领域，传统的加减速算法有直线型、指数型、三角函数型等[7]，许多学者在对加加速度研究的基础上，更加深入地对加加速度进行探索，提出了S形加减速曲线等[8-10]。

笔者结合实际应用，提出一种适配刀片旋转运动的加减速算法，其电机加减速运动学关系如图8所示。

图8 电机加减速运动学关系图

图8中，电机在启动时先作加速度增加的加速运动和加速度减少的加速运动，然后作匀速运动，最后作减速运动。同时，为避免加速度的突变造成的机械柔性冲击，本文将加加速度函数设计为连续的分段函数。

要求出具体时间的速度值，需要求出速度的函数解析式，因为加速、匀速和减速阶段的求解原理类似，所以本文以加速阶段为例进行函数求解。

在[0，t1]中，加加速度函数为3段一次函数，设为：

(17)

式中：k—加加速度函数斜率；t1—电机加速时间。

然后，对加加速度的各分段函数进行逐次积分，再将边界条件代入，求出带有参数k的加速度函数：

(18)

再对加速度的各分段函数进行逐次积分，求出带有参数k的角速度函数：

(19)

最后，对速度的各分段函数进行逐次积分，求出带有参数k的角位移函数：

(20)

求出角速度和角位移函数后，当t=t1时，有vmax=v3(t1)，s3(t1)=α，即：

(21)

式中：t1—电机加速时间；α—加速阶段刀片的角位移。

经整理得：

(22)

即可求出函数中的待定系数，得到加速阶段的速度、加速度和加加速度的函数解析式。

4 基于PLC的加减速控制

为适应复杂的工作环境，系统采用PLC作为控制器。称量系统将称重信号实时在线发送给仪表，仪表与PLC之间采用RS485通讯，当仪表收到的重量信息达到定重要求时，发送信号给PLC，再由PLC控制分剪机执行分剪动作。

PLC程序控制流程如图9所示。

图9 PLC程序控制流程图

在对电机加减速运动进行定量求解后，得到关于参数k和t1的函数解析式，由式(22)可知，需要确定加速阶段的角位移α和vmax。

通过对刀片分剪动作的分析，可以求出电机在加速阶段转过α的角度，匀速阶段转过β的角度，减速阶段转过γ的角度。所以，笔者将刀片设计尺寸和橡胶条空间位置尺寸代入式(7)中,经计算可求出：α=3π/20。

在匀速阶段剪切橡胶条时，因为橡胶条具有独特的弹性和黏性，需要采用样本实验的方法求出最大的剪切速度。经实验得，取步进电机在匀速阶段的转速为5 r/s，即vmax=10π rad/s。

所以，将α、vmax的值代入式(22)中，得：

(23)

再将式(23)代入式(19)中，得：

(24)

根据上式速度公式，取步进电机步距角为1.8°，则可以得到关于时间t的脉冲频率关系式为：

(25)

若通过PLC实时计算上述数据，再输出相应脉冲信号，则由于单次PLC扫描时间内计算量过大，导致PLC无法及时输出相应脉冲信号。需要对速度曲线进行离散化处理。

笔者采用等时长离散化的方法，即将加减速各阶段的总时长划分为许多小区间，在每个小区间上用其中某一点处的速度值来近似代替同一个小区间上的速度值。

等时长离散化处理如图10所示。

图10 电机加减速曲线的等时长离散化处理

通过等时长离散化处理，从而可计算出各分段时间步进电机脉冲序列，如表1所示。

表1 步进电机脉冲序列表

因此，笔者将预先计算好符合S形曲线运动规律的脉冲频率数以数据表的形式存放在PLC存储器中，当PLC按给定规律运行进行速度计算时，直接调用数据库中相应的脉冲频率，可实现分剪机高速、平稳响应，并保证系统的定重分剪精度。

5 结束语

笔者针对高精度挤出橡胶在线定重分剪一体机进行了研究，设计了一种由步进电机控制的同轴反向回转式分剪机构，对分剪机刀具在分剪过程中的运动进行了分析；针对分剪运动及其抑振要求，规划了橡胶分剪运动转角与转速运动规律，推导了一种电机平滑加减速列表控制表达式；基于PLC的控制系统，建立了与实时刀具剪切速度相匹配的脉冲频率数据库，提高了PLC平滑速度控制的实时性。

通过样机试验证明：挤出橡胶在50 g～100 g称量范围内，备料精度稳定地达到±1%的精度，实现了挤出橡胶在线的高精度定重、分剪。