基于制动压力变化率的商用车电控气压转向制动平顺性分析*

杜诗源，杨 凡，李刚炎

(武汉理工大学 机电工程学院，湖北 武汉 430070)

0 引 言

高速行驶的车辆在前方遇到障碍时，通常会执行转向制动操作来确保车辆的行驶安全。但是，当车辆气压制动时，由于供给压力波动、压力传输时延、易泄漏欠压以及电气控制阀的非连续性开关动作等因素影响，导致实际制动压力响应和期望制动压力响应之间存在压力偏差或时间偏差。

通常可采用单位时间制动压力的变化—制动压力变化率，作为电控气压制动系统的评价指标和控制指标[1]。根据力学基础原理，压力变化率对应物体受到的加加速度(Jerk)，对于车辆转向制动过程而言，加加速度能反映车辆的平顺性，且平顺性较车辆安全性和稳定性层级更高。

目前，针对制动压力变化率的研究多集中在乘用车液压制动系统领域。齐志权等[2]基于液压制动系统仿真模型，定量分析了制动系统阶梯减压控制周期和压差与轮缸压力变化率的关系；郜大伟等[3]推导出了轮缸压力变化率模型，并开发了轮缸压力估计车载试验台；徐哲等[4]为了降低液压制动系统内的压力波动，提出了采用稳态压力变化值及压力变化率表征压力动态特性，并推导得到了稳态压力变化值的计算公式；BARTLETT W D[5]提出了在商用车初始增压过程中，由于压力上升速率较慢，而导致车辆实际减速度低于预期，增大制动距离存在危险隐患；王智深[6]提出了由于微泄漏会导致实际制动过程存在欠压，明确了欠压对制动距离和减速度的影响；覃涛[7]定量推导了客车气压制动系统的时延特性，并分析了时延对制动性能的影响。以上研究主要集中在供气压力波动、微泄漏欠压以及制动时延与车辆的制动安全性、稳定性关联分析中，鲜有考虑制动压力变化率对制动平顺性的影响。

本文针对电控气压制动压力变化率概念，采用制动气室充气过程的制动压力变化率计算模型，然后建立制动压力变化率影响下的商用车八自由度整车动力学模型，推导出商用车加加速度的计算模型，并进行分析。

1 车辆电控气压制动压力变化率

GB12676-2014《商用车辆和挂车制动系统技术要求及试验方法》[8]中要求，行车制动系统应能控制车辆行驶，使其安全、迅速、有效停住，制动作用应是渐进的。

为满足车辆行驶安全性、稳定性和平顺性的要求，同时保证制动作用是循序渐进的，需控制单位时间制动压力的变化—制动压力变化率：

(1)

式中:Δpbij—车轮的制动压力偏差，Pa;Δt—制动时间偏差，s；dpbij/dt—制动压力变化率，Pa/s。

制动气室的制动压力响应曲线和制动压力变化率响应曲线如图1所示。

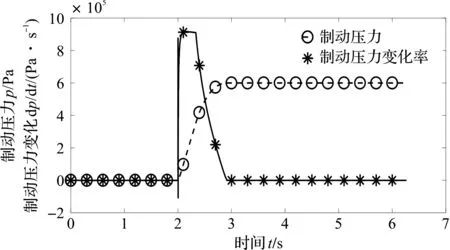
图1 制动气室制动压力和制动压力变化率响应曲线

由图1可知：商用车的制动气室压力上升过程中，制动压力变化率跟随着改变，说明制动气室制动压力响应和制动压力变化率响应同步。

2 转向制动时加加速度计算模型

商用车转向制动时制动压力变化率过大造成加加速度过大，会使车辆受到纵向冲击。假设，商用车关于x-z平面对称，整车质量分为悬挂质量和非悬挂质量两部分，忽略空气阻尼、轮胎滚动阻力、非悬挂质量的侧倾效应以及横纵坡，各轮胎与地面的接触条件相同。

2.1 整车系统动力学模型

商用车转向制动受力模型如图2所示。

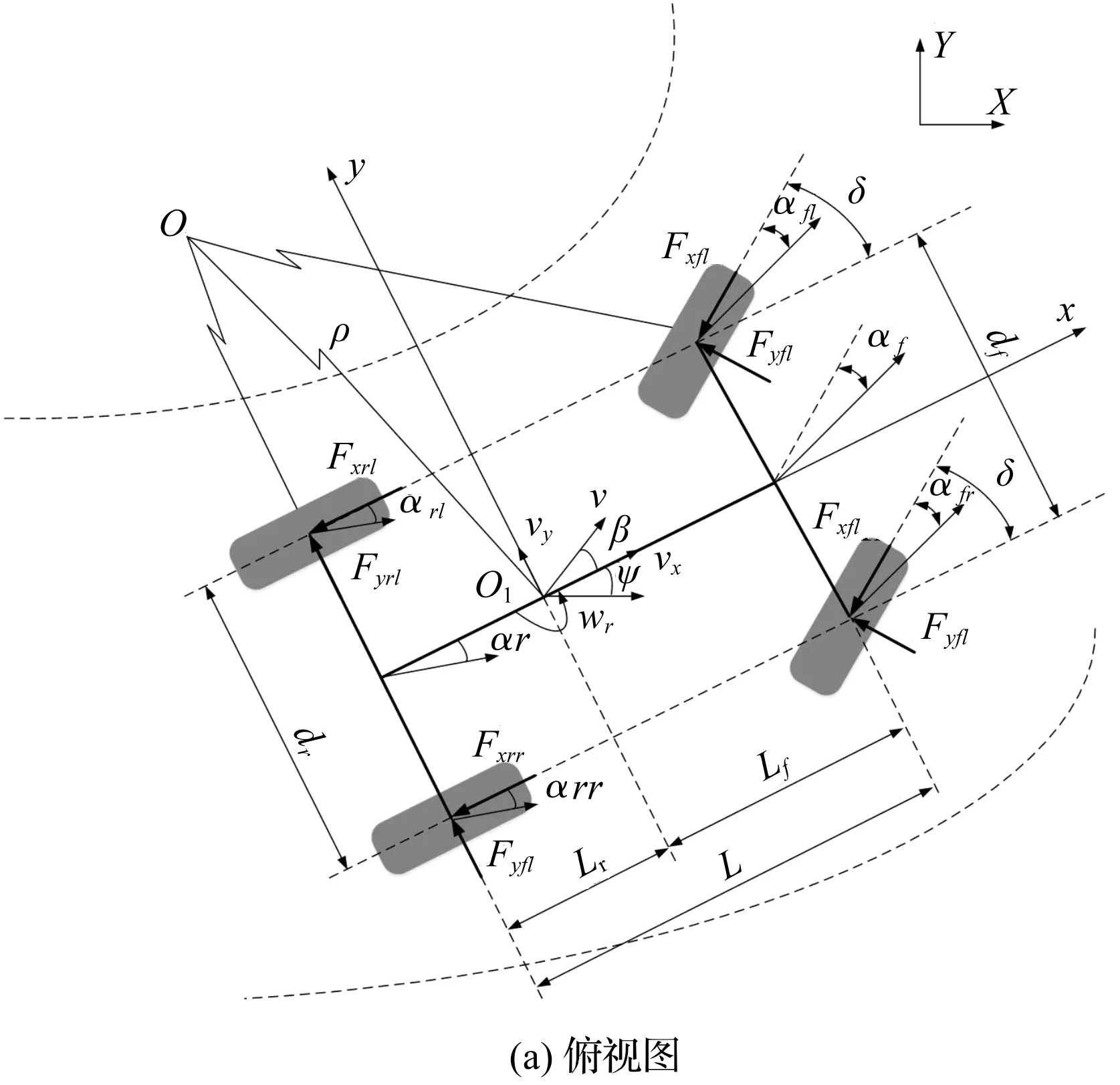
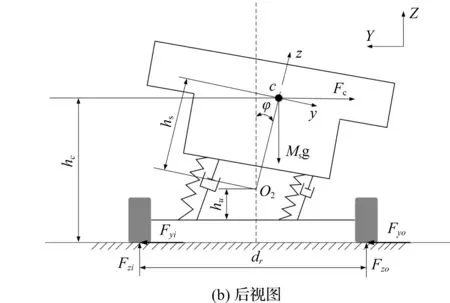
图2 商用车转向制动受力模型

由图2可知：根据假设建立商用车双轴四轮八自由度整车动力学模型，8个自由度包含4个车轮转动，车身纵向、横向、横摆及侧倾运动。

车辆运动基本方程，如下所示：

(2)

(3)

(4)

(5)

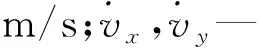
将图2中的地面坐标系与车辆坐标系进行坐标转换；通常商用车左右对称，则Ixz=0；并对式(2～5)求解，可得商用车转向制动行驶状态动力学方程：

(6)

2.2 车轮转动模型

在商用车行车制动过程中，车轮旋转运动如图3所示。

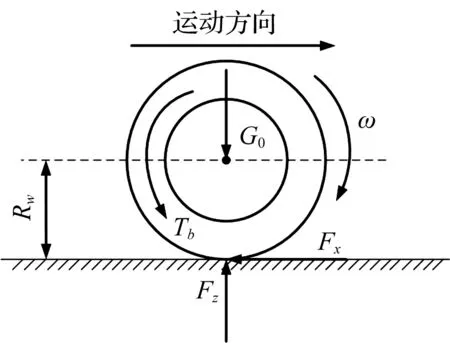
图3 车轮旋转运动

根据各个车轮转动时的力矩平衡，可以得到车轮旋转运动方程：

(7)

式中:ωij—车轮角速度，rad/s；Iwij—车轮转动惯量kg·m2;Tbij—制动器制动力矩，N·m；Rw—车轮滚动半径，m。

2.3 制动器模型

选取盘式制动器作为电控气压制动系统的执行机构。制动压力和制动力矩之间的关系为：

Tbij=AwμbRbpbij=Kbpbij

(8)

式中：Aw—轮胎的制动面积，m2；μb—盘式制动器的摩擦系数；Rb—制动半径，m；Kb—盘式制动器的制动效能因数，N·m/kPa；pbij—车轮的制动压力，kPa。

联立式(7，8)，可推导出制动压力、车轮纵向力、车轮角速度三者之间的关系式：

(9)

2.4 轮胎模型

为了计算方便，轮胎的侧向力计算公式选用轮胎线性模型。为了研究商用车在不同路面上的制动平顺性，轮胎的纵向附着系数选用Burckhardt模型[9-10]，轮胎纵向力计算公式为：

Fyij=-kαij

(10)

(11)

式中:k—轮胎侧偏刚度，N/rad；αij—轮胎侧偏角，rad；Fzij—车轮垂直载荷，N；C1，C2，C3—路面参数，在干沥青路面条件下分别为1.280 1、23.99、0.52。

2.5 车轮侧偏角与纵向滑移率计算模型

各个车轮的轮胎侧偏角为：

(12)

各车轮中心处沿其转动方向的轮速为：

(13)

各车轮的纵向滑移率为：

(14)

2.6 车轮垂向载荷计算模型

考虑侧向加速度和侧倾影响，可得各个车轮的垂直载荷为：

(15)

式中:L—商用车前后轴轴距，m；hc—整车质心高度，m；Mu—商用车非悬挂质量，kg；hu—商用车非悬挂质量质心高度，m；ax—整车纵向加速度，m/s2；ay—整车横向加速度，m/s2。

2.7 制动压力变化率变化时加加速度计算模型

商用车在行车制动过程中，易受到由纵向冲击引起的加加速度。采用加加速度(Jerk)衡量制动平顺性，即：

(16)

式中:v—车身质心行驶速度，m/s；t—制动时间，s。

当Jerk的绝对值在[0 m/s3，5 m/s3]，车辆制动很平顺；当Jerk的绝对值在[5 m/s3，10 m/s3]，车辆制动较平顺；当Jerk的绝对值大于10 m/s3时，车辆制动不平顺[11]。

商用车转向制动时前轮转向角、侧倾角和横摆角通常不超过±15，则可假设sinx≈x,cosx≈1(式中：x-可表示δ、φ和ψ)，联立式(10～12)，则车轮纵横向合力可简化为：

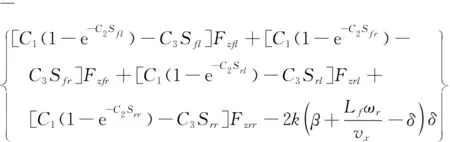
(17)

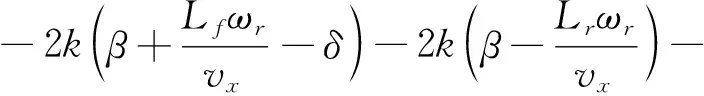
(18)

式(17，18)中的车轮垂直载荷可由式(15)求得，同时纵向滑移率可通过联立式(9，13，14)求得，即：

(19)

其中，pbij可由含有制动压力变化率的函数表示：

(20)

式中：Vc—制动气室的容积，L；Gc—气体质量流量，kg/s；R—气体常数，287J/(kg·K)；θc—制动气室内腔温度，K；dθc/dt—温度变化率，K/s；dVc/dt—制动气室容积变化率，L/s。

联立式(6，16～20)，可以计算出制动压力变化率变化影响下的加加速度：

(21)

由式(21)可知：制动气室压力波动决定制动压力变化率的振荡幅度，进而影响制动器制动力矩的大小，制动力矩又决定车轮纵向滑移率的大小，而纵向滑移率和前轮转向角共同决定轮胎力的大小，从而轮胎力的变化最终影响商用车转向制动过程中的加加速度，且加加速度的大小将反映商用车制动平顺性。

3 基于制动压力变化率的转向制动动力学模型验证

3.1 仿真分析方法与仿真对象

在MATLAB/Siumlink中，笔者搭建基于制动压力变化率的商用车八自由度动力学仿真模型。设定在干沥青路面转向制动，前轮转向角阶跃输入δ=0.04 rad，制动初速度Vc0=20 m/s。

结合工程实际中膜片式制动气室结构参数和工作参数，某型商用车仿真参数如表1所示。

3.2 仿真结果与分析

笔者对制动压力变化率影响下的商用车八自由度动力学模型进行仿真。

商用车转向制动状态参数变化曲线如图4所示。

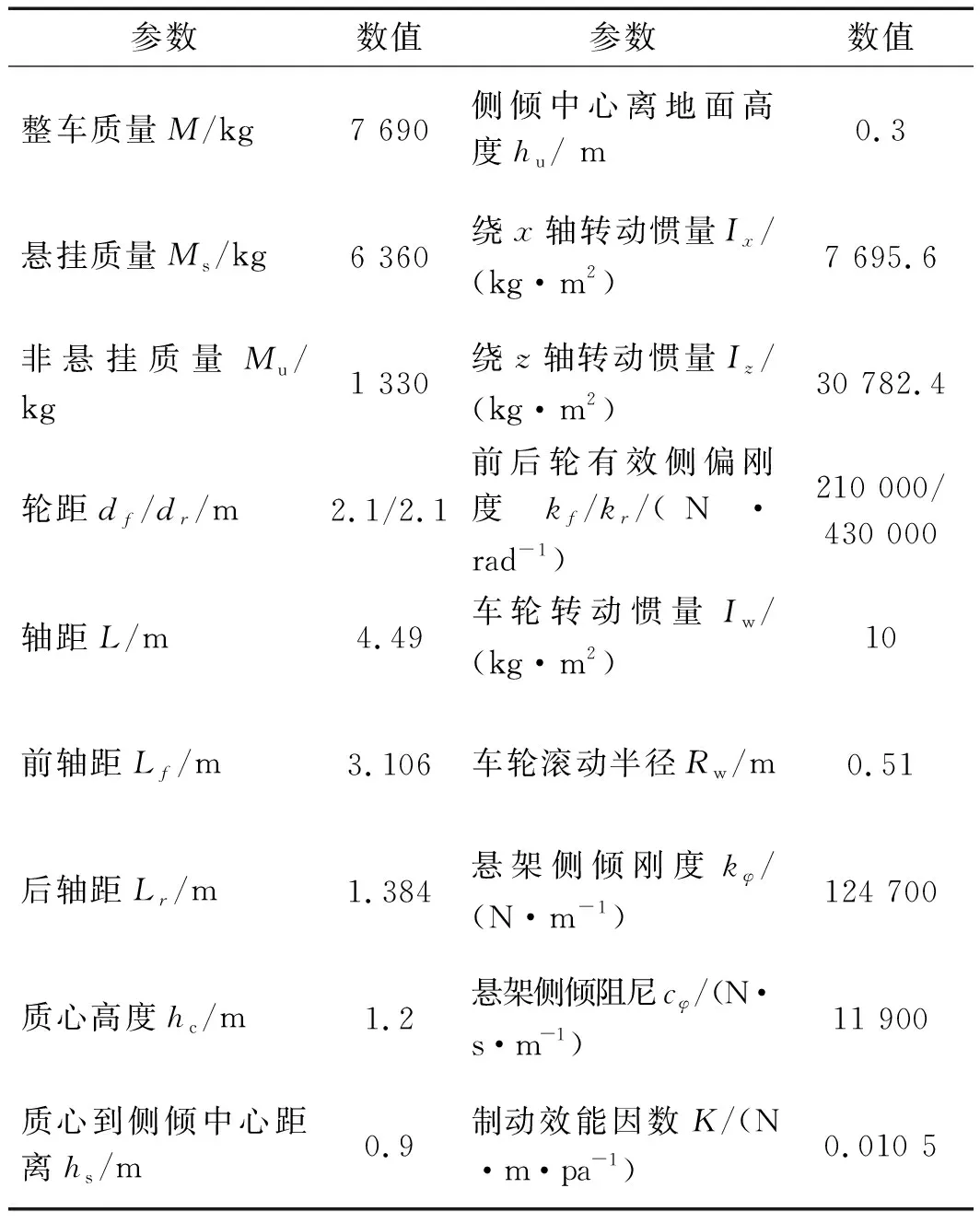
表1 某型商用车仿真参数

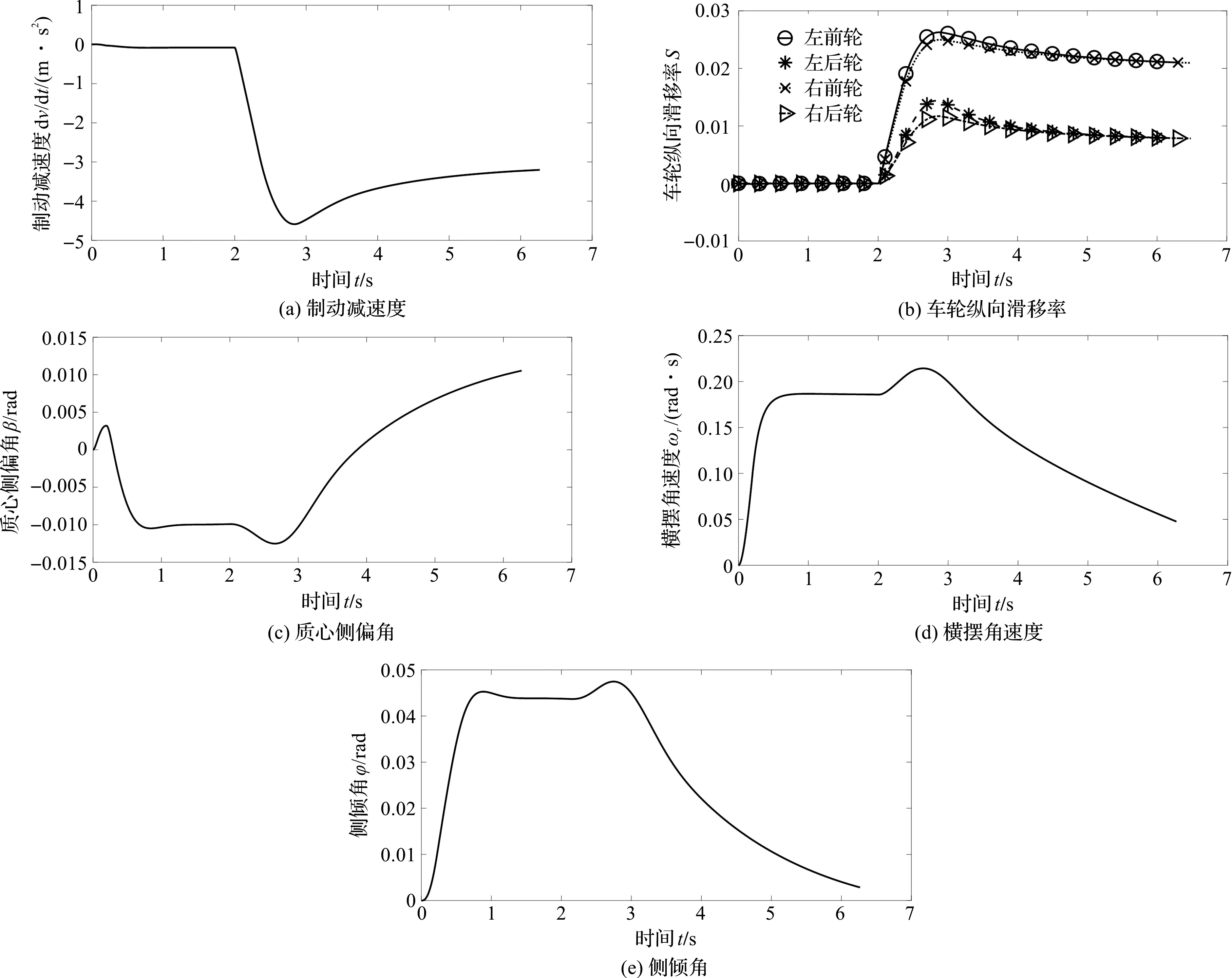
图4 商用车转向制动状态参数变化曲线

由图4可知：商用车的制动减速度逐渐增大再减小，然后趋于稳定；各个车轮的纵向滑移率较小，没有出现车轮抱死的情况；横摆角速度开始时随着前轮转向角输入的增大而增大，到达峰值后又随车速的减小而减小，没有出现异常的变化；质心侧偏角和侧倾角都较小。从定性角度说明，商用车处于稳定行驶状态，在较低车速、前轮转向角输入较小的情况下轻度制动，商用车会保持动力学稳定性。因此，所建立的动力学模型是可用的。

4 转向制动工况下整车平顺性影响分析

4.1 转向制动工况对整车平顺性的影响

笔者采用MATLAB/Simulink软件对整车平顺性模型进行仿真，采用表1数据，以制动压力变化率和前轮转向角为变量，采用单一变量进行分析。前轮转向角为阶跃输入，前轮转向角在0.2 s后上升为最大值，并保持不变；当时间达到2 s时，输入供气压力。设置供气压力ps=600 kPa，改变音速流导，使得制动压力变化率稳态值分别为0.4 MPa/s，0.6 MPa/s，0.8 MPa/s；前轮转向角分别为0.01 rad，0.03 rad，0.05 rad。以制动压力变化率稳态值为变量时，前轮转向角保持0.01 rad不变；以前轮转向角为变量时，制动压力变化率稳态值保持0.4 MPa/s不变。制动初速度设定为20 m/s，仿真结束判断条件为车速，当车速降到5 m/s时，仿真结束。

不同变量下Jerk随时间的变化情况如图5所示。

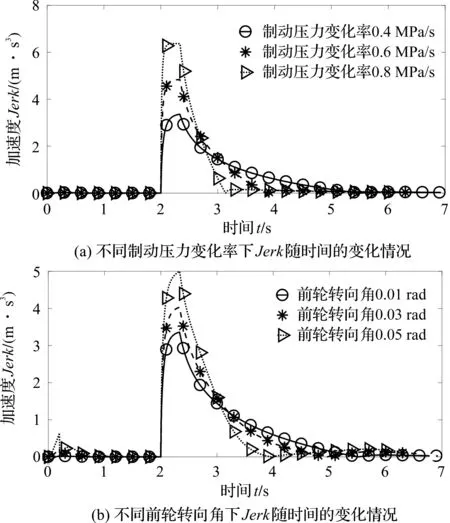
图5 不同变量下Jerk随时间的变化情况

从图5可知：

(1)在转向制动工况下，制动压力变化率稳态值增大，加加速度稳态值随之增大；制动压力变化率稳态值越大，加加速度响应时间越短。因此，制动压力变化率改变对加加速度的大小和响应时间均有影响；

(2)在转向制动工况下，前轮转向角越大，加加速度稳态值越大；随着前轮转向角增大，加加速度响应时间越短。因此，前轮转向角对加加速度的大小和响应时间也均有影响。

通过单一变量下的转向制动工况的加加速度对比，在转向制动的瞬间，加加速度快速上升到稳态值，说明此时整车的制动减速度有一个跃变，而制动压力变化率越大，前轮转向角越大，加加速度达到的稳态值就越大，且响应时间就越短，车辆受到的纵向冲击越剧烈。

4.2 制动压力变化率与整车加加速度的关系

将图1与图5进行比较可发现，Jerk的变化趋势与制动气室制动压力变化率相似，在开始转向制动之后2.4 s左右达到最大值，然后迅速减小，在开始转向制动之后0.4 s左右达到稳态值。

将制动压力变化率与加加速度的数据进行拟合，制动压力变化率上升过程中加加速度变化情况如图6所示。

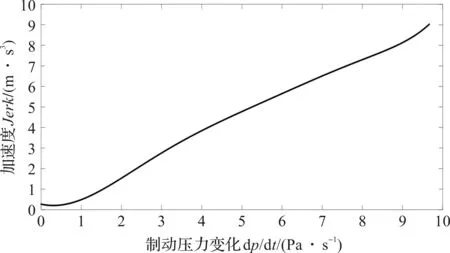
图6 制动压力变化率上升过程中加加速度变化情况

由图6可知：转向制动时，制动气室的压力波动在影响制动压力变化率的同时，也会影响加加速度，从而影响商用车的平顺性。

然后，选择前轮转向角δ=0.01 rad，供气压力ps=600 kPa，制动初速度Vc0=20 m/s进行仿真。

前轮转向角-制动压力变化率临界关系曲线如图7所示。

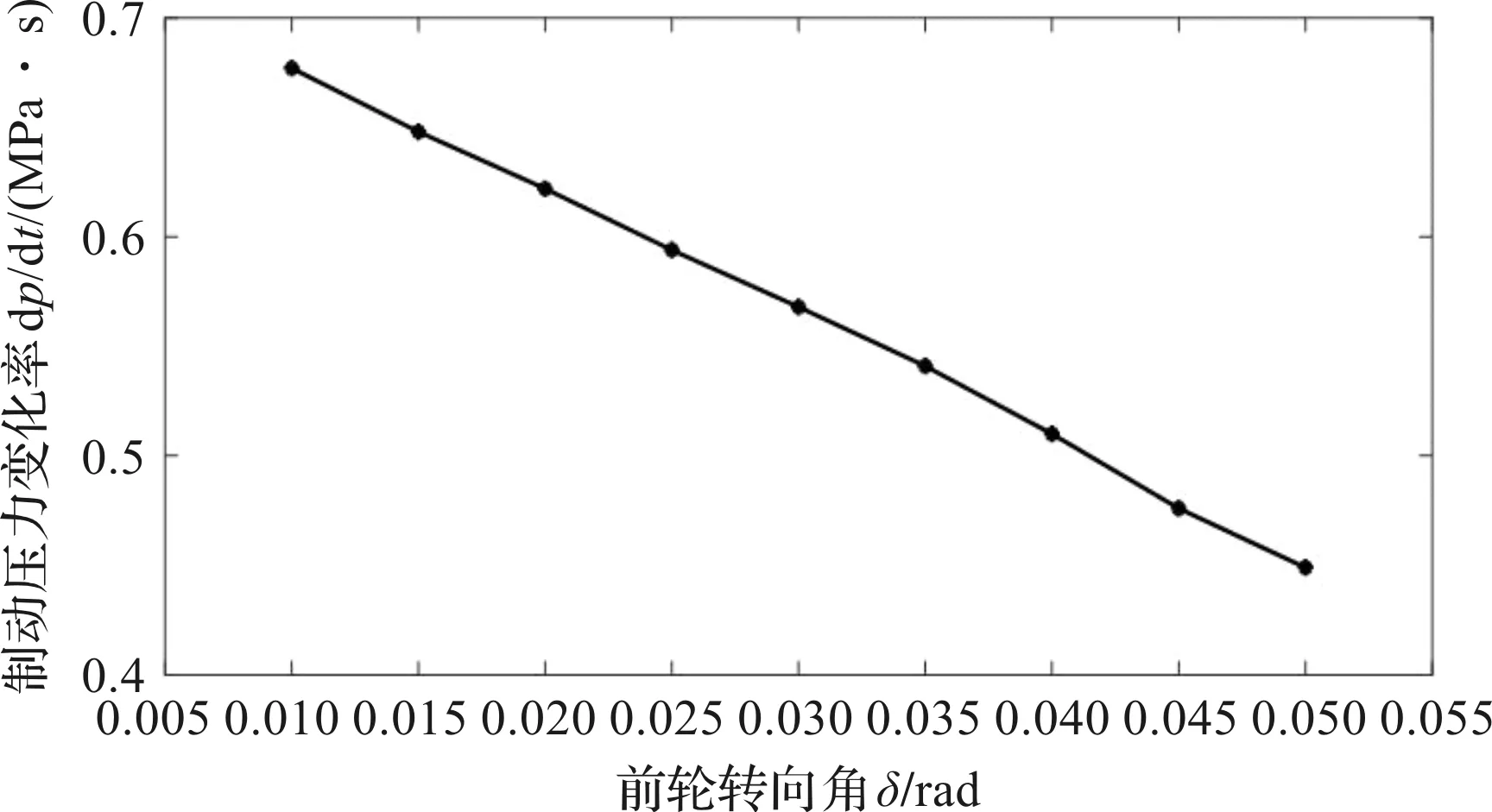
图7 前轮转向角-制动压力变化率临界关系曲线

由图7可知：

(1)曲线下方即为商用车转向制动平顺的前轮转向角以及制动压力变化率；

(2)该前轮转向角下，制动气室临界制动压力变化率约为0.677 MPa/s。通过该方法，分别可以得到前轮转向角为0.015 rad、0.02 rad、0.025 rad、0.03 rad、0.035 rad、0.04 rad、0.045 rad、0.05 rad的制动气室临界压力变化率分别为0.648 MPa/s、0.622 MPa/s、0.594 MPa/s、0.568 MPa/s、0.541 MPa/s、0.510 MPa/s、0.476 MPa/s、0.449 MPa/s。

5 结束语

(1)本文采用制动气室充气过程中的制动压力变化率数学模型，在转向制动工况下，建立了商用车八自由度动力学模型，得到了考虑制动压力变化率变化的加加速度的计算模型；

(2)由建立的商用车整车模型Simulink仿真结果可知，该模型可较好地反映转向制动行驶状态；

(3)通过对制动压力变化率以及整车平顺性的仿真可知，制动压力变化率与加加速度的变化规律相似，且供气压力一定时，制动压力变化率越大；同时，前轮转向角越大，加加速度越大，发生的纵向冲击越剧烈，转向制动平顺性越差；

(4)通过对前轮转向角与制动压力变化率关系进行分析，得出了该车型前轮转向角与制动压力变化率临界关系曲线：当商用车的前轮转向角以及制动压力变化率在该曲线下方时，商用车转向制动是平顺的，纵向冲击在驾乘人员的忍受范围之内。