基于有限元的汽车传动轴模态参数优化研究*

赵生莲，唐 熊，张 健

(攀枝花学院 交通与汽车工程学院，四川 攀枝花 617000)

0 引 言

随着生活水平的普遍提高，用户对商用车的安全性、可靠性、舒适性等方面提出了更高的要求[1]。这也为各大汽车生产商的产品研发指明了方向[2]。

传动轴作为汽车传动系统的重要部件有着较为完善的理论模型。据研究表明，造成传动系统弯曲振动的主要原因是发动机运动部件往复惯性力和传动轴自身的不平衡[3]，并已证实发动机是引起动力传动系统振动的主要原因[4]，当外激振频率与传动轴的一阶固有频率重合时会发生明显的共振，损坏传动轴[5]。此外，来自变速器和地面对车身结构的作用也会引起传动轴的共振，由于外部激励复杂多变，业内普遍通过提高传动轴固有频率避免共振，其方式主要有两种:采用中间支撑，分段传动[6]或采用空心轴传动[7]。

某轻型卡车传动轴在设计阶段进行了模态仿真分析，满足设计要求，但在整车试验阶段存在明显噪声峰值，经过排查，确认与传动轴的振动有关[8]。由于传动轴实际工况复杂,此前学者多以单根轴的自由模态为研究方向[9]，而传动轴在实际工作中存在一定的约束且通常由多段轴通过万向节连接而成。

本研究根据前面学者研究的不足，提出以下改进措施：分别对传动轴各段轴和总成进行相应的模态分析，判断其1阶固有频率是否需要优化；然后进一步利用控制变量法推导出两端无支承、均匀壁厚的传动轴结构与其模态参数的函数关系，并将其作为优化模态参数的依据；最终提出优化并验证可行性。

1 传动轴几何模型建立

本研究根据所选车型传动轴结构参数，利用三维建模软件CATIA建立模型，在保留基本特征的前提下进行适当简化后导入到模态分析软件ANSYS中，并对模型进行材料设置和网格划分，设置材料为40CrNi，材料参数如表1所示。

表1 材料参数

最终所建立的传动轴总成模型单元数是150 886个，节点数281 073个。

2 模态分析理论

2.1 模态分析一般理论

要研究传动轴的动态特性，首先要建立该系统的运动微分方程[10]。一般的，多自由度的动力学的通用方程如下式所示：

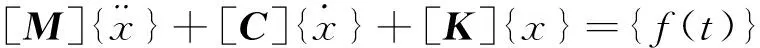
(1)

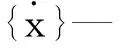
由于只有结构的刚度特性和质量分布影响结构的固有频率和主振型[11]。系统的无阻尼自由振动方程如下式所示：

(2)

其对应的特征方程如下式所示：

([K]-ω2[M]){φ}=0

(3)

式中:ω—系统的固有频率;{φ}—模态振型向量。

求解式(3)可得到传动轴的固有频率和振型。

2.2 模态参数优化标准

发动机是传动轴振动的主要激励源，但变速器与地面的影响同样不可忽视。传动轴的最高转速取决于最高的行驶车速，传动轴最大工作频率与车速关系[12]如下式所示：

(4)

式中:Va—最高车速;fj—传动轴最大工作频率;ij—变速器最高档传动比;io—主减速比;kj—发动机转矩主谐量的阶数;r—车轮半径。

该车最高车速为95 km/h，变速器最高挡传动比为0.784，主减速比为7.02，发动机转矩主谐量的阶数为2，轮胎半径为0.385 m。

经计算，传动轴最大工作频率为120 Hz，考虑到传动轴在使用一段时间后，由于磨损、变形等因素会引起自身不平衡加剧，需要保证传动轴的一阶模态频率比其临界转速对应的频率高15%[13]，经计算为138 Hz。

2.3 传动轴结构对模态参数的影响

笔者采用控制变量法，根据两端自由支撑、壁厚均匀的传动轴临界转速的经验公式，分别分析传动轴长度和壁厚对其模态参数影响的变化规律，结果如下：

(5)

式中:nC—传动轴第一阶固有频率;L—传动轴长度，取两万向节之中心距;d，D—轴管的内、外径。

3 有限元模态分析

3.1 主传动轴自由模态

本研究对主传动轴进行自由模态分析，得到其前六阶自由模态振型，主传动轴各阶振型及位移图如图1所示。

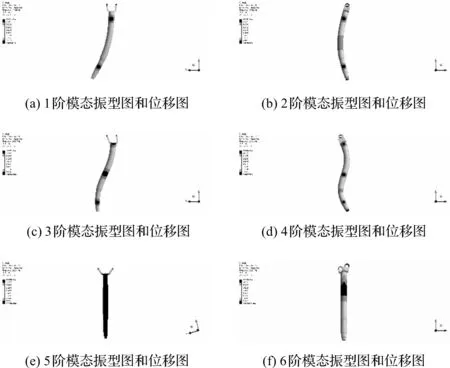
图1 主传动轴各阶振型及位移图

图1(a)为传动轴一阶模态计算结果，其一阶固有频率为447.89 Hz，模态变形表现为传动轴绕X轴方向一阶弯曲;图1(b)为传动轴二阶模态计算结果，其二阶固有频率为455.821 Hz，模态变形表现为传动轴绕Z轴方向一阶弯曲;图1(c)为传动轴三阶模态计算结果，其三阶固有频率为1 151.50 Hz，模态变形表现为传动轴绕X轴方向二阶弯曲;图1(d)为传动轴四阶模态计算结果，其四阶固有频率为1 231.10 Hz，模态变形表现为传动轴绕Z轴方向二阶弯曲;图1(e)为传动轴五阶模态计算结果，其五阶固有频率为1 319.40 Hz，模态变形表现为传动轴法兰叉扩张振动;图1(f)为传动轴六阶模态计算结果，其六阶固有频率为1 521.70 Hz，模态变形表现为传动轴呼吸振动。

3.2 中间传动轴自由模态

笔者对中间传动轴进行自由模态分析，得到其前六阶自由模态振型，中间传动轴各阶振型及位移图如图2所示。

图2 中间传动轴各阶振型及位移图

图2(a)为传动轴一阶模态计算结果，其一阶固有频率为103.12 Hz，模态变形表现为传动轴绕X轴方向一阶弯曲;图2(b)为传动轴二阶模态计算结果，其二阶固有频率为103.14 Hz，模态变形表现为传动轴绕Z轴方向一阶弯曲;图2(c)为传动轴三阶模态计算结果，其三阶固有频率为284.09 Hz，模态变形表现为传动轴绕X轴方向二阶弯曲;图2(d)为传动轴四阶模态计算结果，其四阶固有频率为284.75 Hz，模态变形表现为传动轴绕Z轴方向二阶弯曲;图2(e)为传动轴五阶模态计算结果，其五阶固有频率为544.27 Hz，模态变形表现为传动轴绕X轴方向三阶弯曲;图2(f)为传动轴六阶模态计算结果，其六阶固有频率为546.61 Hz，模态变形表现为传动轴绕Z轴方向三阶弯曲。

3.3 传动轴总成约束模态

为还原传动轴总成的装车工作状态，本研究对传动轴总成进行相应的约束，传动轴总成施加约束结果如图3所示。

图3 传动轴总成施加约束结果

本研究分析得到传动轴总成前六阶约束模态振型，传动轴总成各阶振型及位移图如图4所示。

图4 传动轴总成各阶振型及位移图

图4(a)为传动轴一阶模态计算结果，其一阶固有频率为132.82 Hz，模态变形表现为中间轴绕Z轴方向一阶弯曲;图4(b)为传动轴二阶模态计算结果，其二阶固有频率为135.87 Hz，模态变形表现为中间轴绕X轴方向二阶弯曲;图4(c)为传动轴三阶模态计算结果，其三阶固有频率为244.66 Hz，模态变形表现为主传动轴绕-X轴与Y轴角平分线方向一阶弯曲;图4(d)为传动轴四阶模态计算结果，其四阶固有频率为245.86 Hz，模态变形表现为主传动轴绕X轴与Y轴角平分线方向一阶弯曲;图4(e)为传动轴五阶模态计算结果，其五阶固有频率为379.94 Hz，模态变形表现为中间轴绕Z轴方向二阶弯曲;图4(f)为传动轴六阶模态计算结果，其六阶固有频率为388.46 Hz，模态变形表现为中间轴绕X轴方向二阶弯曲。

通过模态分析对比发现中间传动轴一阶固有频率与发动机激振频率存在重合，因而需进行模态参数优化。

4 传动轴结构与模态参数的关系

4.1 传动轴长度与模态参数的关系

笔者分别取传动轴轴管长度为815 mm、1 015 mm、1 215 mm、1 415 mm、1 615 mm，得到不同轴管长度的传动轴一阶固有频率如表2所示。

表2 不同轴管长度的传动轴固有频率

根据分析结果作传动轴轴管长度与传动轴一阶固有频率关系图如图5所示。

图5 传动轴轴管长度与其一阶固有频率关系图

由图5(a)可以看出，传动轴的第一阶固有频率值随轴管长度的变化分布近似于一条二次曲线，利用数值分析方法中的最小二乘法对后3个离散点进行曲线拟合，设频率与轴管长度的关系可用二次方程来表示，则求出的曲线方程为：

nC=201L2-773.88L+884.12

(6)

由图5(b)可以看出:除了长度为0.815 m的点外，可以看出两者具有很好的一致性，说明当传动轴的长度大于1 m后，可以近似认为轴管长度与其一阶固有频率呈线性关系。而当轴管长度小于1 m时，传动轴第一阶固有频率随着长度的减小增大较快。

4.2 传动轴壁厚与模态参数的关系

笔者分别取传动轴壁厚为4 mm、4.5 mm、5 mm、5.5 mm、6 mm，得到不同轴管壁厚的传动轴一阶固有频率如表3所示。

表3 不同轴管壁厚的传动轴固有频率

根据分析结果作传动轴轴管壁厚与传动轴一阶固有频率关系图如图6所示。

图6 传动轴轴管壁厚与其一阶固有频率关系图

由图6(a)可以看出，传动轴一阶固有频率与轴管厚度的关系曲线近似于一条二次曲线，同样使用最小二乘法求解其近似二次方程，求得的二次方程表达式为：

nC=-0.26D2+10.93D+152.32

(7)

由图6(b)可以看出:所求二次方程曲线与计算真实值具有极高的一致性，说明传动轴的轴管厚度与其一阶固有频率呈二次线性关系。

5 传动轴的改进

笔者通过对比汽车发动机激振频率120 Hz和最大危险共振频率138 Hz，发现其与传动轴总成一阶固有频率132.82 Hz存在重合，传动轴在工作中有存在共振的可能，因此需对传动轴进行结构改进，以避开共振频率范围。

经过多次模态分析比对，笔者得出保持传动轴内径不变，通过减小中间传动轴轴管厚1 mm能有效避开共振频率范围。

根据ANSYS计算求解结果，笔者提取优化后的传动轴总成的前六阶非刚体约束模态参数。

改进前后模态数据对比如表4所示。

表4 结构改进前后模态数据对比

6 结束语

(1)笔者以某轻型卡车的传动轴为研究对象，根据影响传动轴模态参数的因素，利用控制变量法和最小二乘法推导出了模态参数与轴管长度和壁厚的线性变化关系函数；

(2)将上述关系函数作为模态优化的依据，结合仿真分析验证发现，通过减小中间传动轴轴管壁厚能有效提高传动轴总成一阶固有频率，因此采用了在保证中间传动轴内径不变的情况下，减小其轴管壁厚1 mm的方法进行了优化；

(3)优化结果显示，在保证传动轴轴管强度前提下，传动轴总成一阶固有频率从原来的132.82 Hz提高到138.49 Hz，高于发动机激振频率120 Hz 的15%，满足了避免共振的要求。