参数化局部特征尺度分解及其在复合故障诊断中的应用研究*

朱文民，喻 宇，薛海峰

(1.中铁隧道集团一处有限公司，重庆 401121；2.昌九城际铁路股份有限公司，江西 南昌 330000；3.重庆大学 机械传动国家重点实验室，重庆 400030)

0 引 言

机械设备作为工业生产中的基础设施，其安全、高效的运行是生产的保障。在机械设备中，齿轮和滚动轴承作为其中最为重要的两个零件，往往是影响设备安全运行的重要因素[1]。因此，对于齿轮和滚动轴承的状态监测显得尤为重要。目前，对于单个部件的故障分析已具有较成熟的理论研究和实践分析，但对于其组合故障的研究甚少[2]。

机械设备的检测往往是通过信号进行表征，但是无法从信号中读取该设备的健康状态。

时频分析方法作为一种常用的信号处理方法，其可以对信号进行深层次的处理，得到具有明显状态特征的信息量。

小波分析作为一种典型的信号分析方法，其可以把一个复杂的信号分解为若干具有特征意义的单分量，但是小波分析无法实现参数的自适应[3-4]。

经验模态分解(EMD)和内禀时间尺度分解(ITD)作为典型的时频分析方法，其通过极值点的包络分析，分别经过包络筛分和插值得到若干单分量信号[5-6]。但是EMD方法仍然存在严重的包络和模态混淆问题[7]，ITD方法没有阐述合理的数学物理含义[8-9]。

通过对ITD方法的进一步探讨，郑近德等人[10-11]提出了具有明确物理意义的局部特征尺度分解(LCD)方法，但是LCD中三次样条插值在一阶求导处容易发生突变，致使分解的单分量失真；文献[12]将Hermite插值与ITD方法相结合，使得信号分解更加完全，分解分量更加真实，适合于非线性复杂信号。但是Hermite插值在确定插值空间时，其拟合曲线将固定，无法再次调整曲线达到理想效果[13-14]。鉴于此，论文提出了结合Hermite插值，并植入参数，在LCD基础上提出了参数化局部特征尺度分解(PLCD)方法。PLCD方法利用参数化Hermite插值进行了包络，并依据中间极值对称为最优拟合判定原则，建立了合适的分解基函数，并进行了迭代更新来实现最终的分解，其既克服了EMD方法的包络问题，也改善了Hermite插值的性能。

基于以上分析，本文针对机械设备复合故障信号的多个分量信号耦合特性以及强非线性，通过在Hermite插值中植入参数，使其变得具有可调性，得到更具光滑性、可靠性的参数化内禀尺度分量(PISC)；通过分析仿真信号和复合故障信号，以证明所提方法具有良好的分解性能。

1 参数化局部特征尺度分解方法

LCD方法采用三次样条插值解决了信号的分解过程中毛刺现象，使得分解具有明确的物理意义，但是其本身的三次样条插值在一阶求导处常表现出突变状态，致使分解得到的分量出现能量泄露、失真等现象[15-17]。

针对该问题，Hermite插值作为一种成熟的曲线拟合方法，其获得的曲线具有平滑性，并且插值更具效率性，有效地克服了三次样条插值的不足。但是，Hermite插值在插值完成后，无法进一步修正，不具可调性。

鉴于Hermite插值的缺点，笔者在Hermite插值中引入可调参数，构造参数化Hermite插值方法，通过调整可调参数可以进一步逼近理想曲线，提高拟合精度。

参数化Hermite插值方法通过调整参数，可以有效地完成信号的有效分解，解决突变、平滑性等问题。

PLCD方法的具体流程可以表述为：

第一步：找出输入信号X(t)中的所有极大值点和极小值点(Xk(k=1,2,…,M))，并记录相应的时刻(τk(k=1,2,…,M))。

根据PLCD算法的要求，必须设置一个构造参数a，并建立基线信号表达式：

(1)

第二步：利用参数化Hermite插值对基线信号进行插值，同时，设定步长，调整可调参数λi，利用式(2)的参数Hermite插值对式(1)的基线信号Lk进行插值，最终可以得到最佳的L1。

其参数化Hermite插值表达式如下式所示：

Fi(t)=1+(λi-3)t2-(2λi-2)t3+λit4
Fi+1(t)=-(λi-3)t2+(2λi-2)t3-λit4
Gi(t)=t+(λi-2)t2-(2λi-1)t3+λit4
Gi+1(t)=-(λi+1)t2+(2λi+1)t3-λit4

(2)

式中：Fi(t)，Fi+1(t)，Gi(t)，Gi+1(t)—参数化Hermite插值可调基函数；λi—可调参数。

第三步：执行X(t)-L1，分离出L1，最终可以获得P1。判断P1是否是一个合适的PISC分量，给出两个约束条件：

(1)对于分解出的PISC，相邻的极值点具有符号差异性；

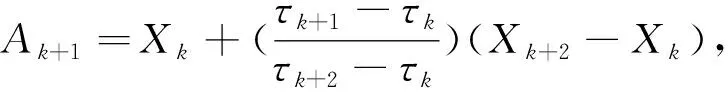
第四步：判定P1如果满足上述两个约束条件，即为第1个PISC。同时，对于一个满意的PISC，其Lk+1应满足为0的条件，但是实际信号具有复杂性，不可能达到理想的效果，这时设定一个允许的变动量Δ，即满足|Lk+1|≤Δ。

第五步：判定P1如果不满足上述两个约束条件，则进一步把P1作为待分析原始信号，然后执行第一步至第四步，当执行k次后，得到的Pk符合约束条件，这时将得到第1个理想分量PISC1。

第六步：从x(t)中分离出得到的第1个分量，然后获得余量信号r1，将余量信号r1作为一个新的信号来重复第一步至第五步，即可得到第2个分量。以此类推，当执行n次时，得到满足约束条件的n个单分量。执行完一次循环之后，判断余量信号是否为单调函数，如果是则终止分解，否则再次循环。因此，可以表述为下列公式：

(3)

由此可见，通过结合参数化Hermite插值和LCD算法，可以实现分量信号的平滑性，避免了分量失真和能量泄露。同时，调整可调参数λi，可以使得拟合曲线逼近于理想分解曲线。

2 复合故障信号仿真分析

为了测试所提PLCD方法的应用效果，本文拟构造一复合故障仿真信号进行分析，复合故障包含齿轮故障和滚动轴承故障。

构造等式如下式所示：

x2(t)=

(1+0.6+0.5cos(20πt))sin(0.2(sin20πt))+

0.5cos(2π×5t)

x(t)=x1(t)+x2(t)+n(t)

(4)

式中：n(t)—高斯白噪声。

设定信噪比为5 dB；固有频率为fn=3 000 Hz；齿轮转频为fr=40 Hz；滚动轴承的故障频率为fg=100 Hz；采样频率为fs=8 192 Hz；给定位移数为x0=5；阻尼系数为ε=0.1；固有圆频率为ωn=2πfn。

复合故障仿真信号时域波形图如图1所示。

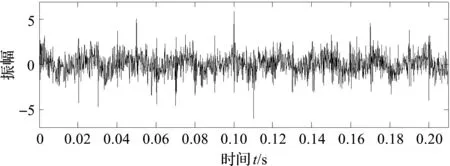
图1 复合故障仿真信号波形图

在图1中，其时域图表现出一定的调幅调频特征，但无法读取该信号的故障状态。因此有必要对该信号进行进一步分析。

频谱分析和包络谱分析作为经典的特征表征和信息增强方法，其可以突出信号的故障特征，均取得了良好的应用效果，信号x的包络谱图如图2所示。

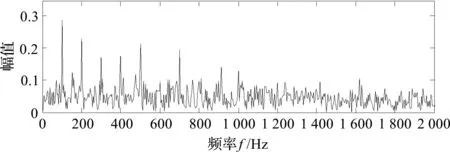
图2 复合故障仿真信号包络谱图

从图2中可以看出：在滚动轴承的故障频率及倍频处具有明显的峰值，可以判定滚动轴承具有故障。但是，在齿轮的故障频率处并没有明显的谱线，无法判断齿轮故障。

因此，需要对信号进行分解分析，把齿轮故障分量信息和滚动轴承故障分量信息从原始信号中分离出来，完成对轴承故障的有效判断。

这里笔者采用EMD、LCD和PLCD方法分别对原始信号进行分解，其分解结果如图3所示。

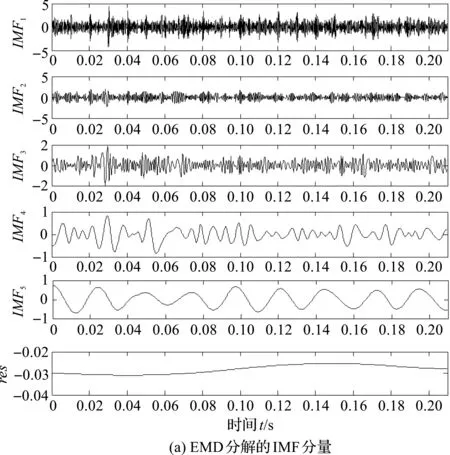
从图3中可以发现：所得分量信号都具有更加明显的幅值调制信息，可以大致判定该信号存在故障，但是具体故障仍无法判断。

因此，笔者对3种方法得到的分量做包络谱分析。

包含主要特征信息的前几个分量包络谱如图4所示。

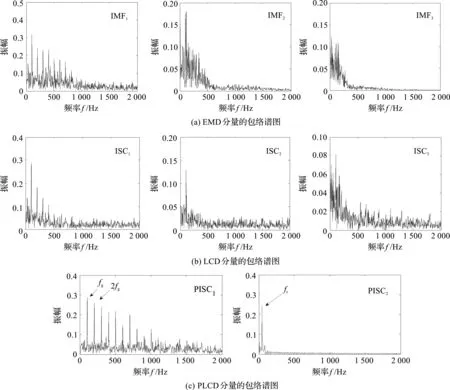
图4 3种分解方法的包络谱

从图4中可以看出：

(1)EMD方法的分量包络谱给出了更加明显的滚动轴承特征频率及倍频，坚定了滚动轴承故障的存在，但是对于齿轮故障信息还是无法获取；

(2)LCD的包络谱相比较于EMD有更加明显的优势，噪声干扰成分更少，不过齿轮故障信息仍没有被分离；

(3)PLCD方法采用参数化Hermite插值，使得拟合曲线更加趋近于理想分量曲线，筛选出齿轮故障信息，所得包络谱中突出了齿轮故障特征。

因此，通过3种方法的分解对比分析可以证明，笔者所提的PLCD方法具有更优越的分解性能。

3 实际复合故障信号分析

通过仿真信号的分析，证明了所提方法的优越性能，但是在实际信号中的效果如何，需要进一步探讨。因此，笔者据此搭建了一复合故障模拟试验台。

复合故障实验台如图5所示。

图5 复合故障实验台

在图5中，笔者选择6307型号的滚动轴承进行实验，同时在轴承的外圈上切割一个深0.15 mm和宽0.15 mm的线槽，用来模拟滚动轴承外圈故障。

另外，实验选用的一对齿轮均为37齿，在从动轮的齿根部切割一个深0.12 mm和宽0.12 mm的线槽，用来模拟齿轮裂纹故障。

在实验过程中，笔者拟采用加速度传感器来拾取振动信号，轴的转速为900 r/min，设定采样频率为8 192 Hz。通过计算可得齿轮的故障频率为fr=15 Hz，滚动轴承外圈的故障频率为f0=31 Hz。

为了判断该振动信号的故障状态，笔者做出了该信号的时域波形图和包络谱。

复合故障信号的时域波形图和包络谱如图6所示。

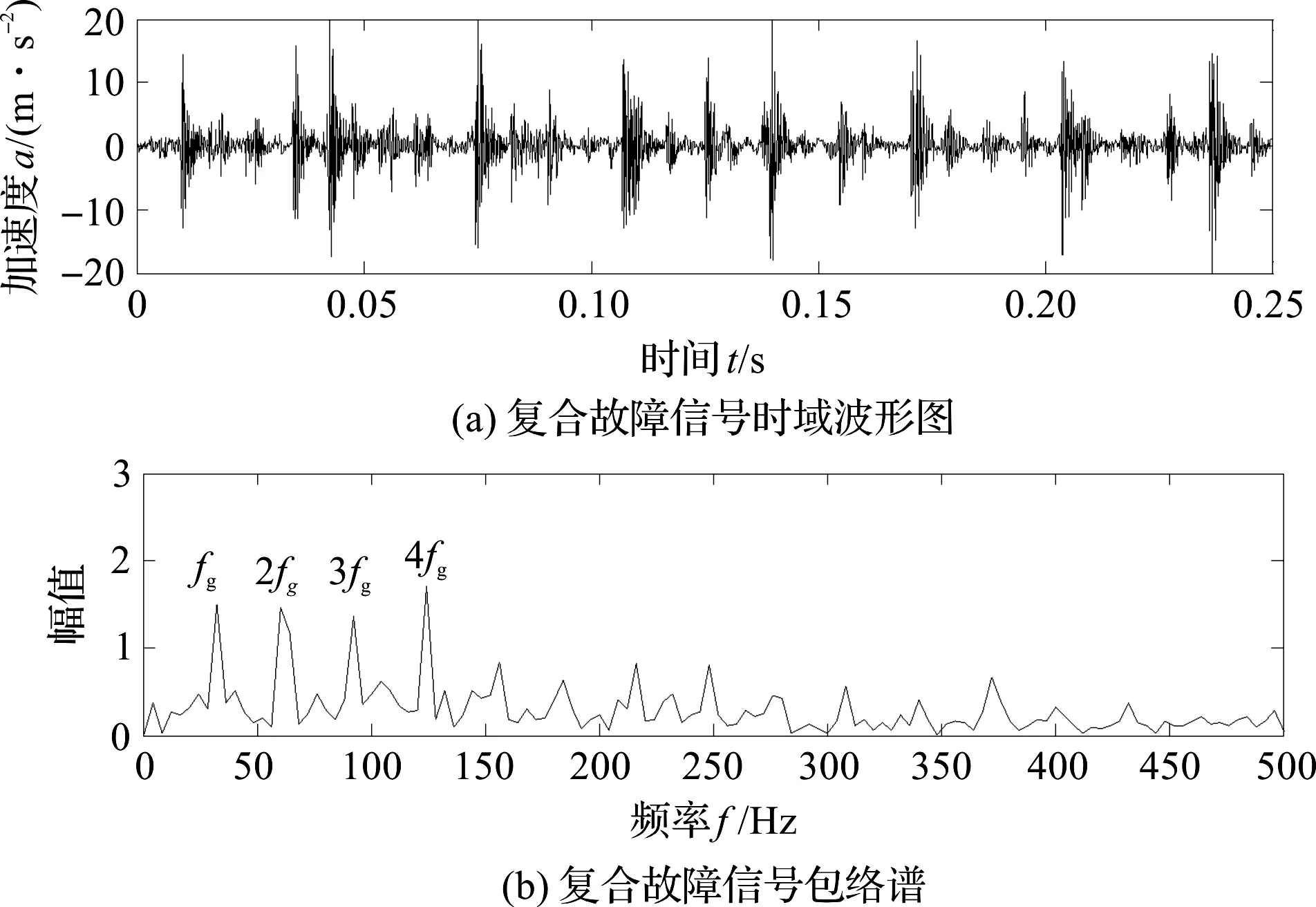
图6 复合故障信号的时域波形图和包络谱

从图6可以看出：

通过分析时域波形图中的冲击成分和包络谱中的故障频率，可以断定其具有滚动轴承外圈故障，但无法断定齿轮的状态。针对这种状况，笔者拟对时域信号进行分解，将齿轮故障信息从滚动轴承及噪声分量中分离出来，完成故障的诊断。

由于实际工况的多变性，以及机械设备内部结构的复杂性，采集的信号往往包含多种对象的分量信号，它们之间相互耦合，构造出一个非线性调幅调频信号。

笔者采用EMD、LCD和PLCD方法分别对复合故障振动信号进行分解，分解结果如图7所示。

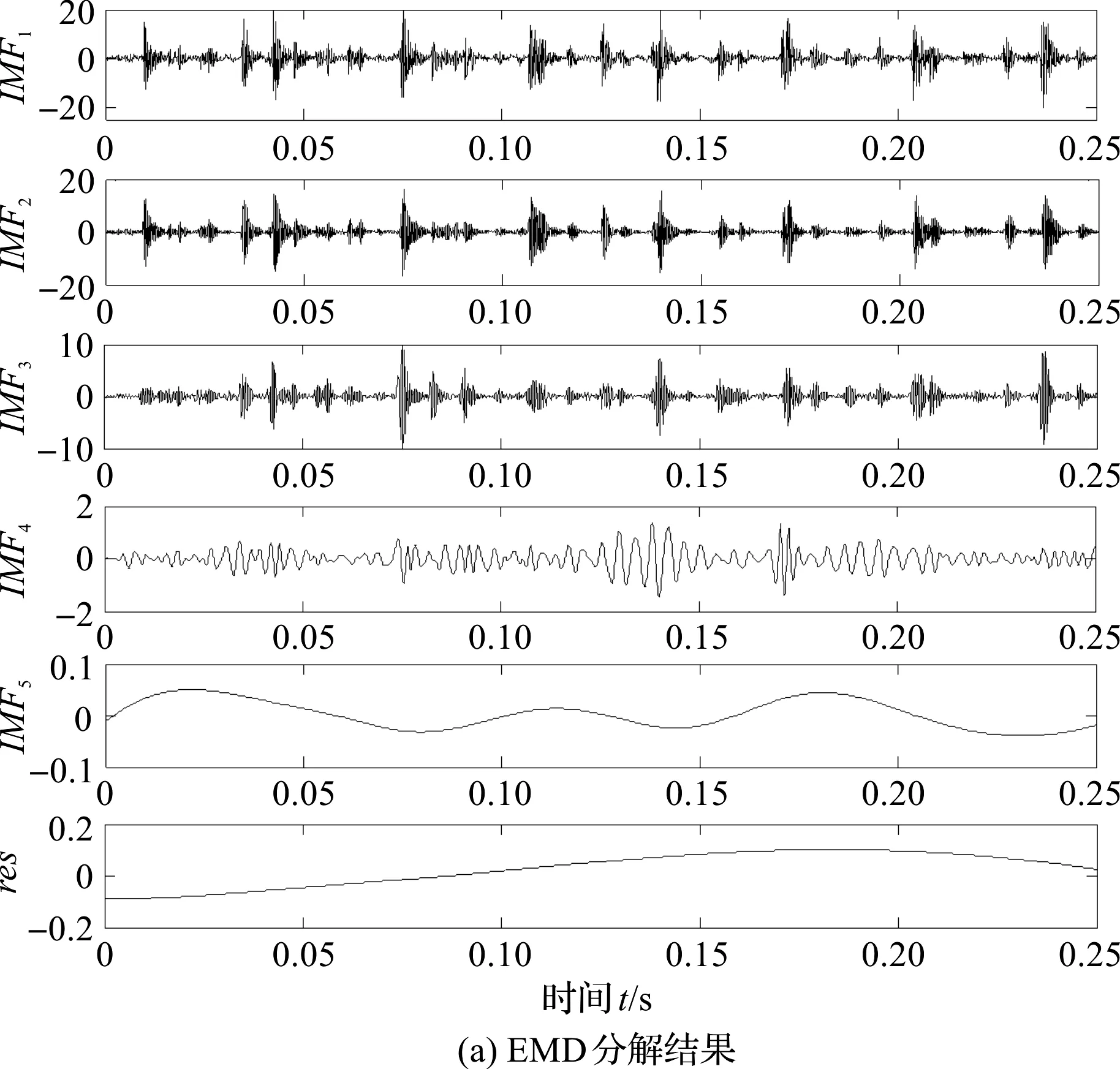
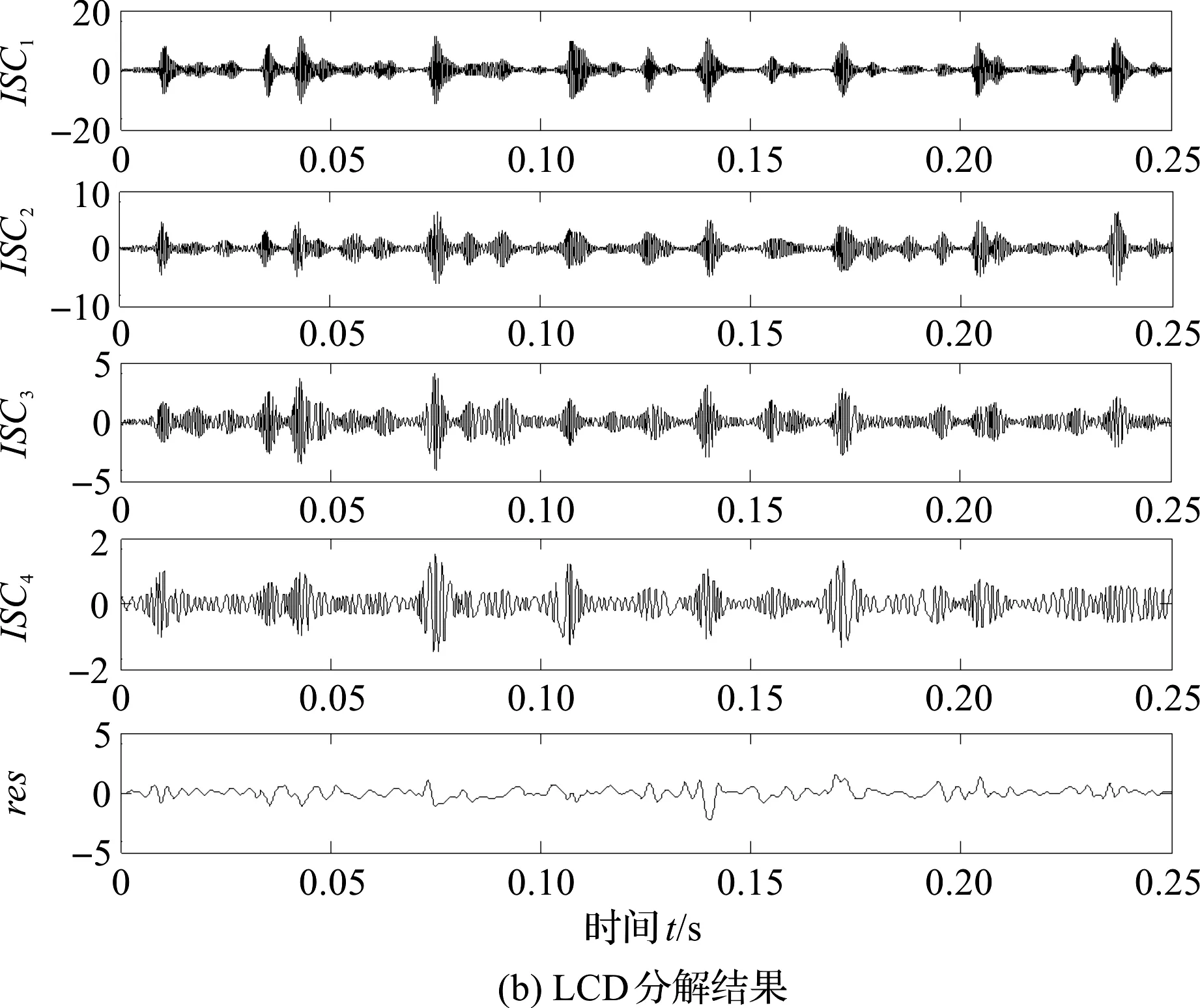
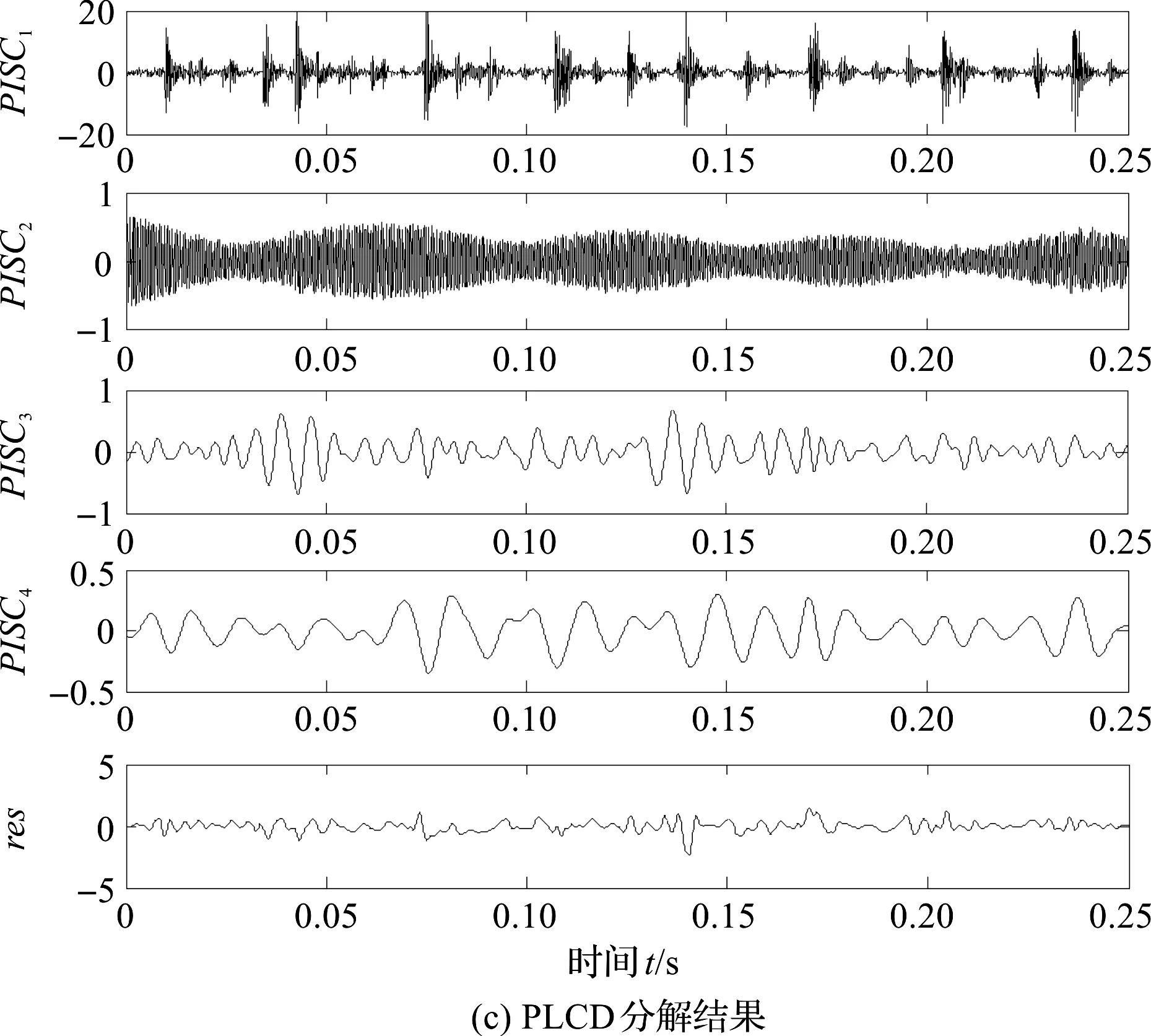
图7 3种分解方法的分解结果

图7(a)中，前几个分量均表现出明显的幅值调制信息，但齿轮故障信息无法捕捉；

图7(b)中，有用信息更加集中，幅值调制更加明显，但是仍然难以凸现齿轮的故障信息；

图7(c)中，PLCD只分解出3个分量，第1个分量和第2个分量具有明显不同的调制信息，第1个分量冲击较为明显，与滚动轴承故障特征相吻合。第2个分量调制较为缓慢与齿轮啮合故障相契合，可以初步判定极可能出现齿轮故障。

因此，仅从时域波形进行分析时，可以证明PLCD具有优越的分解性能。

为了准确判断滚动轴承和齿轮是否具有故障，笔者进一步做出分量包络谱，分析结果如图8所示。

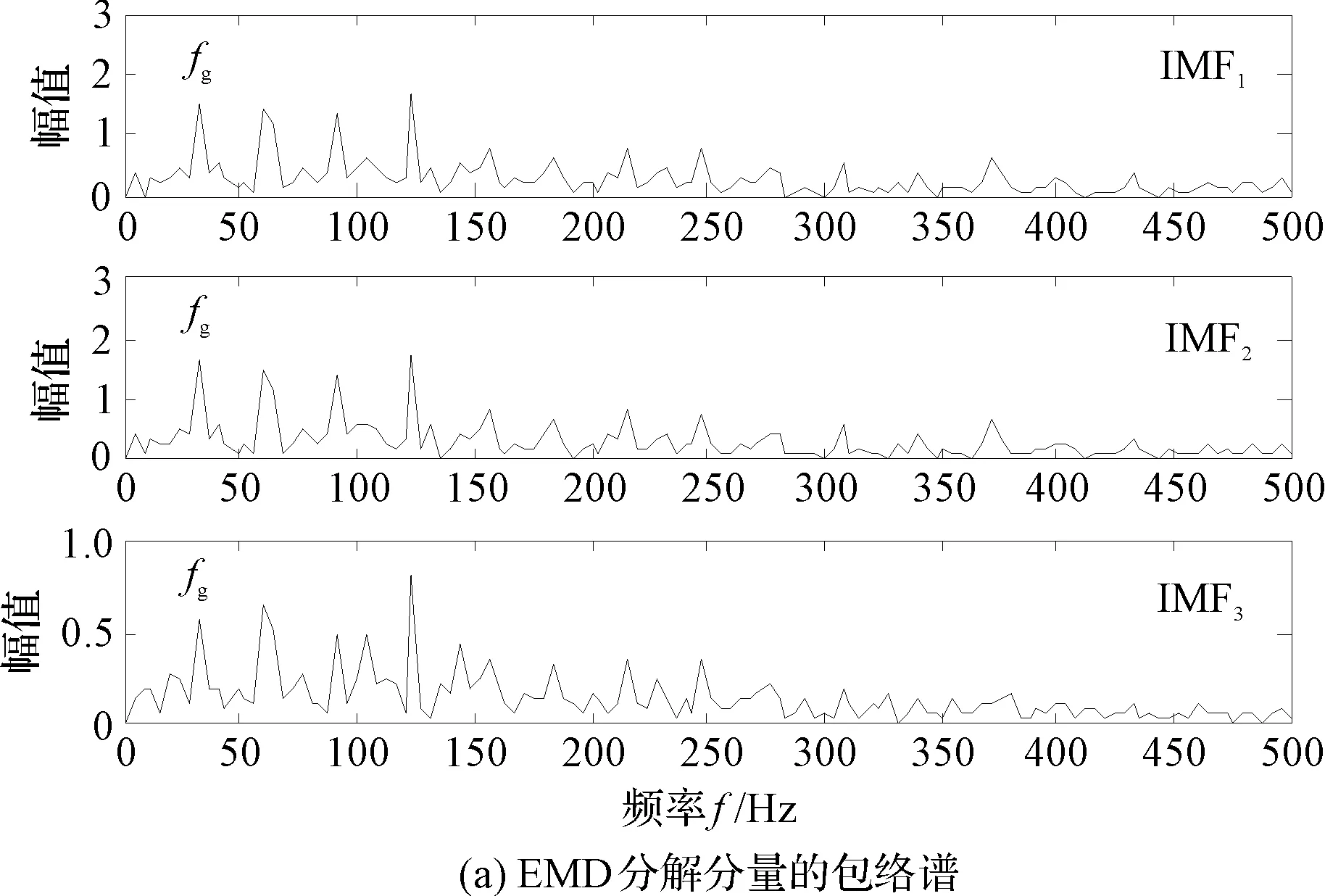
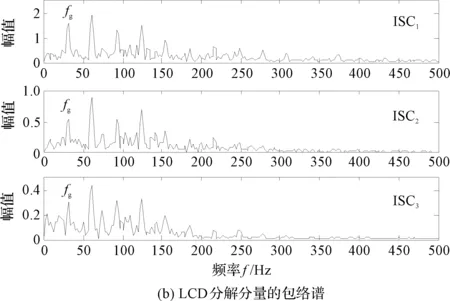
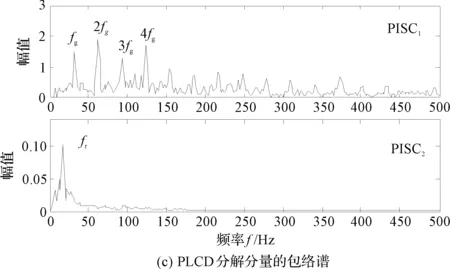
图8 3种分解方法的包络谱分析

图8(a)为EMD分解分量的包络谱，可以发现齿轮的故障信息仍然没有被凸现出来，无法判定齿轮故障；

图8(b)为LCD的前4个分量包络谱，其仍然只能展示滚动轴承故障信息；

图8(c)为PLCD分解得到的前2个分量包络谱，第1个分量展示了滚动轴承外圈故障信息，具有明显的外圈故障特征频率及倍频成分。第2个分量在齿轮的故障频率处具有一个明显的峰值，可以判定该齿轮发生故障。

因此，从3种方法的包络结果可以看出，PLCD方法可以有效地分解出齿轮故障成分，明显优于EMD和LCD方法。

评判一个分解方法的优劣，除了分解性能之外，分解效率也是一个重要指标。

笔者利用4种分解方法分解同一个复合故障振动信号，其分解效率(时间)如表1所示。

表1 3种分解方法的分解效率比较

从表1可以看出：EMD、LCD和PLCD都具有极高的分解效率，EMD效率最佳、PLCD次之、LCD最差。

但是3种方法都可以满足工程的需要，因此，PLCD在具有更加优越的分解性能前提下，也具有极高的分解效率，满足工程实际的需要。

综上所述，笔者分别从分解性能和分解效率两方面比较了3种分解方法。从比较分析中可以看出：

(1)EMD虽然是一个比较经典的分解方法，具有不错的分解性能，但是其对于复杂信号的分解并不能让人满意；

(2)LCD脱胎于EMD方法，比EMD具有更好的分解效果。但是其在分解信号时的三次样条插值对信号的类型比较敏感，无法分离复杂信号中的微弱有用信息；

(3)PLCD继承了LCD的优点，并采用参数化Hermite方法进行插值拟合，具有良好的分解效果，并保持了其分解效率。

4 结束语

本文提出了一种参数化局部特征尺度分解方法，并将其应用于仿真复合故障诊断和实际复合故障诊断中，均获得了良好的应用效果，从中可以得出以下结论：

(1)所提方法利用参数化Hermite进行曲线拟合，通过调整可调参数让拟合曲线更加趋近于理想曲线，可以获得更加光滑、连续的拟合曲线；

(2)将所提方法应用于复合故障诊断中，其可以从复杂信号中将有用的微弱信息完成分离，便于故障诊断的有效进行。

但是任何一种方法都不是完美无瑕的，笔者所提参数化局部特征尺度分解方法同样存在一些问题需要进一步研究：如参数化Hermite的参数设置，如何自适应地选择一个最合适的可调参数等，这将是下一步的研究重点。