支持RFID供应链路径追溯查询的偏增向量编码策略
廖国琼 杨乐川 张海艳 杨仙佩
(江西财经大学信息管理学院 南昌 330013)
无线射频识别(radio frequency identification, RFID)技术是一种非接触性自动识别技术[1].由于具有无需人工干预、批量识别等优点[2-3],该技术已广泛应用于供应链、图书馆、交通等领域,以实现对物品的全程跟踪及监控.但如何对物品在流通过程中产生的海量信息进行编码以支持路径追溯查询,是基于RFID供应链系统面临的主要挑战[4-6].
通常,衡量一个编码策略性能指标主要有查询效率、更新开销及存储开销等[7].然而,供应链环境中路径编码还应考虑3个问题:
1) 环路问题.物品在供应链中流通时,可能多次经过同一地点,即在路径中出现环路.例如,在路径A→B→A中,物品2次经过地点A.因此,良好的路径编码策略应能对环路进行描述.
2) 实时更新问题.为满足实时查询需求,编码策略应能及时将来自RFID读写器的原始数据转化成编码数据,即能对位置信息进行实时更新,实现随到随编.
3) 溢出问题.海量RFID数据会导致编码的码值超出规定数据类型的表示范围,称为溢出现象.一个好的编码策略应能减缓码值的增长速率.
RFID供应链中物品最初提出的路径编码方法为素数编码[8-9],即对路径中结点分配唯一素数,并利用素数乘积因式分解唯一的特性进行解码.素数编码在查询方面具有较高效率,但其不能解决环路问题,且面对海量RFID数据时,素数增长过快,码值容易溢出.为解决单一编码的不足,文献[10]提出了一种素数编码与区间编码相结合的复合编码(composite coding, CC)策略,即对路径的位置信息采用素数编码,时间信息采用区间编码[11-12],并针对溢出问题提供了路径分裂方法,能满足路径查询需求,但此方法不能描述环路,且更新代价较大,不利于实时更新.
针对环路问题,文献[13]提供了一种在素数编码下描述环路的方法,其主要思想为将环路中重复的位置给予相同的素数,在计算同余值时按结点重复次数以幂次进行计算区分.此方法有效地编码了环路,但增加了同余值计算复杂度,且未考虑时间信息.文献[14]提出一种改进的素数编码方法,位置信息编码充分利用值较小的素数,时间信息编码则利用可持久的区间编码(durable region based numbering, DRB)方法编码,能减缓素数溢出,但减缓程度有限,且解码时耗较大,影响查询效率.文献[15]提出了一种路径分裂策略对路径编码树进行分裂,但查询会涉及多张表,导致查询开销增加.
RFID供应链系统还有一类针对减少存储空间的压缩编码策略,如pid编码[16]和基于T树的路径压缩策略[17].类似前缀编码,pid编码存储会产生较大冗余.基于T树的策略不涉及具体编码,而是用T树来构造编码树提升查询效率,但此方法在构建树的过程中开销较大.
综上所述,已有RFID对象路径编码方法都只适用于一定场合,不能完全解决供应链环境路径编码的环路、实时更新及溢出等问题.
向量编码(vector coding)是针对XML文档提出的一种层次编码方法[18],该编码基于2个向量之间可以无限插入向量的思想对一个对象分配一对向量,具有较高的查询效率和更新效率.但向量编码的码值是基于区间编码产生的,即先对结点进行区间编码,然后再将区间转化成向量进行编码,不能随到随编,实现实时更新.而且,不能解决海量RFID数据导致的码值溢出现象.
本文将在原始向量编码基础上,研究一种偏增向量编码(offset addition vector coding, OAVC)策略及优化策略.该策略可直接对RFID对象的时空信息进行向量编码,可有效提高编码效率,且在综合考虑查询效率、更新效率及支持环路、溢出等方面具有较好性能.
1 供应链下RFID路径表示及编码框架
附有RFID标签的物品在供应链上流通时,会被不同位置的阅读器识别,生成形如(TagID,Loc,Time)形式的原始数据流,其中TagID是标签对象的唯一标识,Loc和Time分别表示识别地点及时间.图1是来自不同阅读器48条未加工原始数据样例.
通常,RFID读写器会以固定周期扫描其探测区域内RFID标签对象,因此同一个标签对象可能被同一读写器扫描多次,故原始数据中存在大量冗余信息.实际上,我们只需记录标签在某位置的进入时间和离开时间,即将同一个标签对象在同一个位置的多条原始数据转换成1条数据存储,即TagID:Loc[ST,ET],其中ST表示TagID对象进入位置Loc的时间,ET表示TagID离开Loc的时间.

Fig.1 RFID raw data record图1 RFID原始数据记录
图2(a)是图1中48条原始数据转换后的数据.可以看出,每条数据可描述某物品在某位置的停留时间.例如Tag1:B[4,6]表示标签对象Tag1在时刻4进入位置B,时刻6离开,故Tag1在位置B的停留时间为2.
为便于查询,我们在转换后的数据中再添加1个层级属性l,用于描述对象在移动路径中的位置序号.例如Tag1:B[4,6,2]表示B是Tag1路径中第2个经过的位置.
于是,我们将属于同一标签对象的数据进行组合,即可得到形如TagID:L1[ST1,ET1,l1]→L2[ST2,ET2,l2]→…→Ln[STn,ETn,ln]的路径信息,如图2(b)所示.

Fig.2 RFID data after processing图2 加工后的RFID数据
我们将包含时间和位置信息的每个路径结点Loc(ST,ET,l)称为时空数据结点,并以此为编码对象进行编码,以支持路径追溯查询.本文采用的编码框架如图3所示:

Fig.3 Framework of RFID path coding图3 RFID路径编码框架
首先,各RFID读写器将原始数据上传给中央服务器.然后,中央服务器对数据进行转化处理,并对每条时空信息进行编码.最后,将每个物品对象,按经过的位置顺序生成各自路径信息,且将每条路径中结点的编码根据时空顺序形成路径树,以表的形式存入数据库供应用层查询.
2 偏增向量编码策略
本节将在文献[18]所提出的向量编码上研究一种能支持追溯查询且溢出速率较低的偏增向量编码策略.
2.1 基本向量编码
偏增向量编码仍采用平面直角坐标系中的第一象限中的向量进行编码.该方法跳过基本向量编码中的区间转化的过程,直接根据结点进入顺序按更新规则得到向量编码.
对于向量编码,有如下定义及定理[18]:
定义1.一个向量V可表示为平面直角坐标系第一象限中的1个坐标(x,y),其中x,y都为整数,如图4(a)所示.
定义2.对于任意2个向量V1(x1,y1),V2(x2,y2)和1个标量r,则有:
V1+V2=(x1+x2,y1+y2),
(1)
r×V1=(r×x1,r×y1).
(2)
定义3.设G(V)为向量V(x,y)的倾斜度,则可表示为G(V)=y/x,即图4(a)中的tanθ.
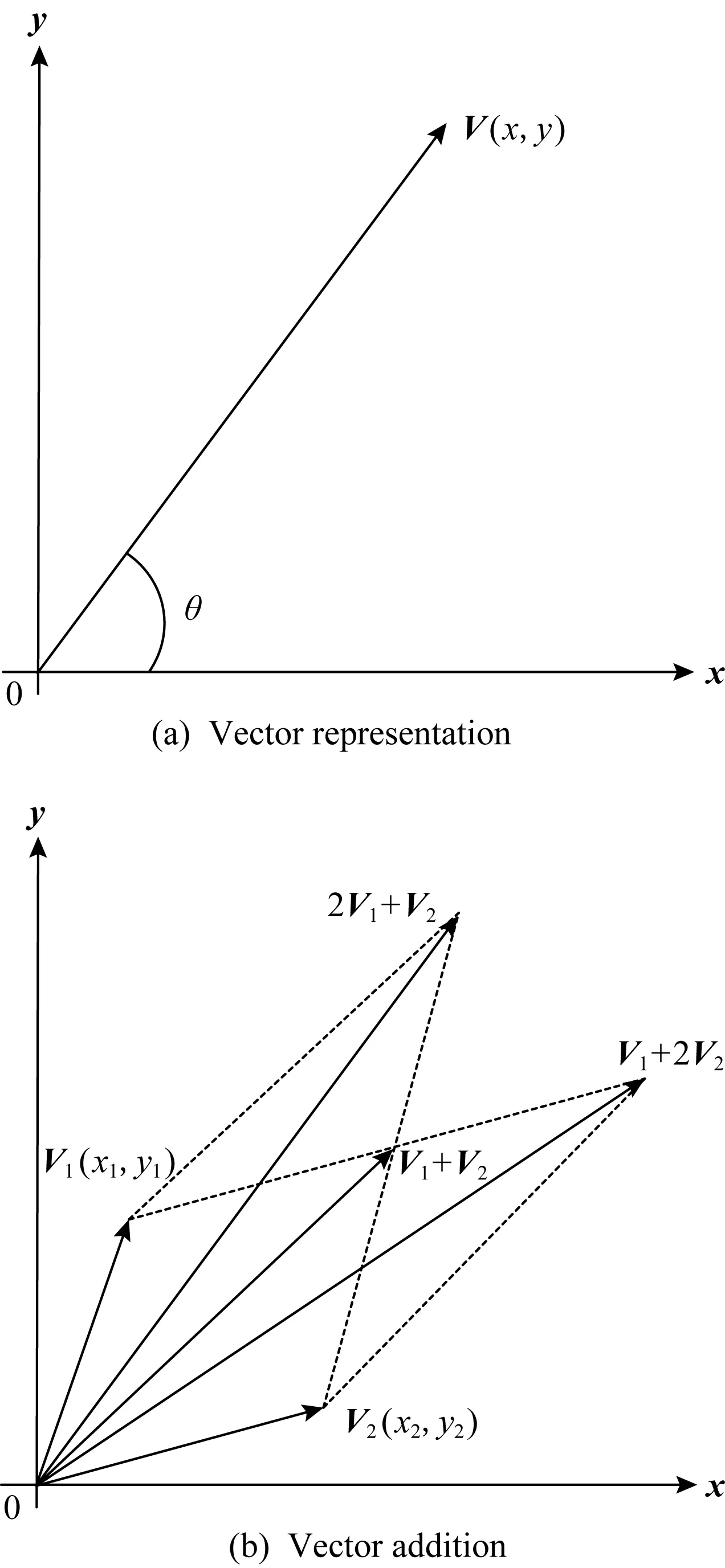
Fig.4 Vector diagram图4 向量示意图
定义4.设GS(V)为向量V(x,y)的粒度,则可表示为GS(V)=x+y.
定理1.给定2个向量V1(x1,y1)和V2(x2,y2),若y1x2>x1y2,则G(V1)>G(V2).
定理2.给定2个向量V1和V2,若V3=V1+V2且G(V1)>G(V2),则G(V1)>G(V3)>G(V2).
定理3.给定2个向量V1和V2,则一定存在无数个向量,其倾斜度都在G(V1)和G(V2)之间.
根据定理2和定理3,如图4(b),向量2V1+V2,V1+V2,V1+2V2都会在向量V1和V2之间.
因此,可以根据结点位置不同,选择(V1+V2,V1+2V2)或(2V1+V2,V1+V2)进行编码.因在V1和V2之间可以反复进行向量加法运算,得到无数个不重复向量,故结点更新变得容易.
2.2 偏增向量编码原理
基于上述原理,给出偏增向量编码(OAVC)策略的基本规则:
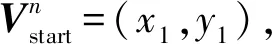
规则2.路径编码树的根定义为虚结点,其码值固定为((1,0)(0,1),0).
编码结点按其更新位置分为4类:无兄弟结点、仅有左兄弟结点、仅有右兄弟结点、既有左兄弟结点又有右兄弟结点.根据其位置不同,确定合适的偏置向量进行编码.
规则3.设编码结点n,其层级为l,p是其亲代结点,cps是最邻近n的左兄弟结点,cfs是最邻近n的右兄弟结点,v1和v2为n的偏置向量,则有4种情形:

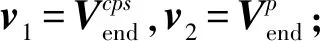

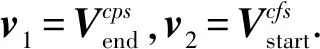
为尽可能减小码值,应考虑v1,v2的粒度大小以决定最后的码值,因此有规则4:
规则4.若GS(v1)>GS(v2),则其编码为((v1+v2,v1+2v2),l);反之,则为((2v1+v2,v1+v2),l).
为了判别结点之间子亲代关系,有定理4.

在编码时,若数据全部按时间先后顺序,每个结点的ST值从小到大进入服务器,同层级自左向右编码,则只需进行规则3的情形1)2)编码.然而,各地阅读器由于距离与速度等原因,到达中央服务器的时间会不一样.因此,当到达顺序发生错乱时,可用规则3的情形3)4)调整顺序.这样做的好处在于:一方面能做到任意时刻任意位置进行实时更新;另一方面能保证整棵编码树完全按时间先后顺序排列,在进行基于时间的查询时提高查询效率.
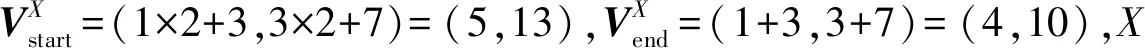
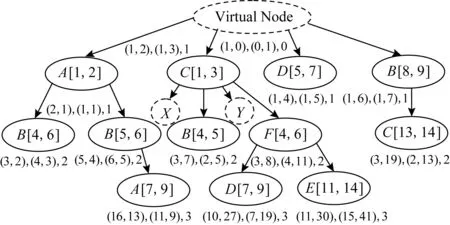
Fig.5 Coding tree of offset addition vectors图5 偏增向量编码树
通过编码树的生成过程可以知道,偏增向量编码的本质是在一定角度内无限地划分角度来表示结点,其思想与区间编码划分区间来表示结点十分类似.但是,区间编码通常是整数区间,需等待数据到达后再进行编码,否则会因整数不可再分而出现大面积更新.而偏增向量编码结点更新时不会影响其他结点,可做到随到随编,满足实时更新及查询需求.
同时,偏增向量编码的对象是时空数据结点,环路问题也能得以解决,因为环路的本质是物品经过同一位置多次.我们可以用编码中的时间信息区分同一位置的每一次经过.例如图5中路径A[1,2]→B[5,6]→A[7,9],A[1,2]与A[7,9]表示2个不同结点,因为它们经过A的时间不同.
然而,偏增向量编码是通过向量相加的形式得到新结点的编码,码值增长较快.对于海量RFID数据,可能会导致码值溢出,故需进行优化.
2.3 向量码值优化
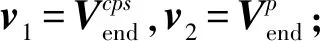


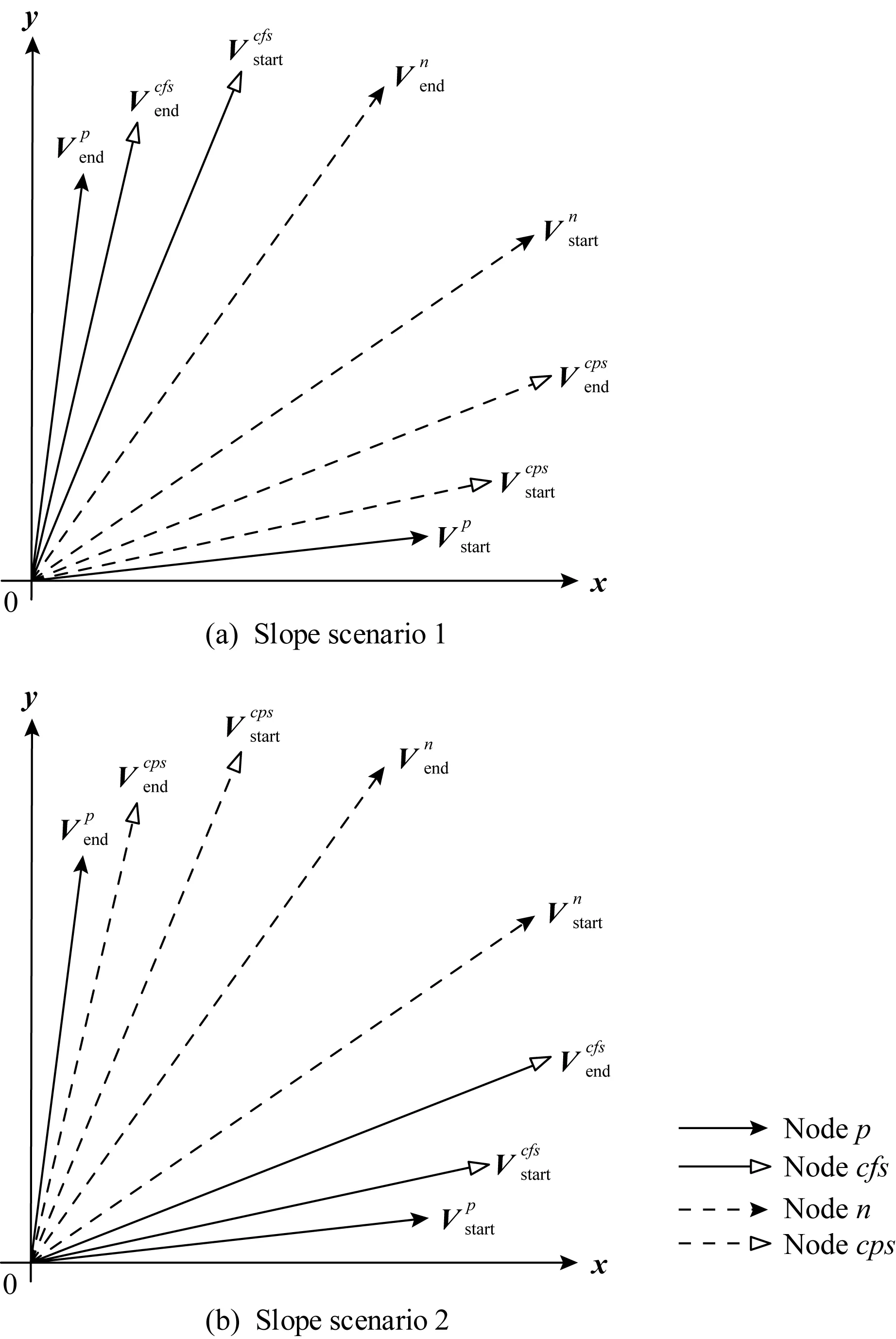
Fig.6 The coded graph in different slope order图6 不同斜率顺序排列下编码示意图
根据上述优化思想,可得优化偏增向量编码(optimized offset addition vector coding, OOAVC)算法如算法1所示.
算法1.优化偏增向量编码算法.
输入:结点n其父结点、最近邻左、右兄弟结点的编码p,cps,cfs;
输出:结点n的编码code.

②flag=0; /*斜率如图6(a)所示排列*/
③ ifn有左兄弟结点

⑤ else

⑦ end if
⑧ ifn有右兄弟结点

⑩ else
根据优化后的算法可以得到新的编码树如图7所示,图7中结点X的码值为(4,11),(5,14),2,结点Y的码值为(5,12),(7,17),2.
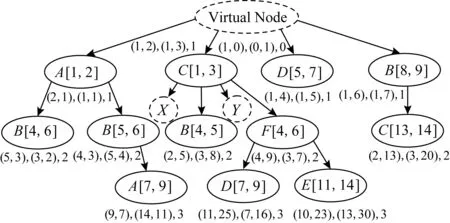
Fig.7 OOAVC coding tree图7 OOAVC编码树
从结果上对比可以看出,OOAVC相比于OAVC,亲兄弟结点中首个结点码值会略微偏大,但其后所有兄弟结点的码值都会偏小.
2.4 优化偏增向量编码亲子代关系证明

证明.




由1)2)可得:
又由定理2得,G(v1) 因2v1+v2=(v1+v2)+v1,得G(v1) 因v1+2v2=(v1+v2)+v2,得G(v1+v2) 综上,优化偏增向量编码仍满足亲子关系. 证毕. 为了便于查询,我们将路径树转化3个数据库中的表进行存储. 1) 标签表(tag table).存储标签号(TagID)及路径编号(PathID),以方便查询物品所在路径,如表1所示: Table 1 Tag Table表1 标签表 2) 路径表(path table).存储路径编号及该路径当前末尾结点的编码((VSx,VSy),(VEx,VEy)),用于根据子亲代判断定理确定整条路径,如表2所示. 3) 时间表(time table).存储编码值以及结点时空信息,其中((VSx,VSy),(VEx,VEy),Level)表示编码,Loc(ST,ET)表示时空信息,如表3所示. 为提高查询和更新效率,在进行路径查询或更新时,我们将从表3提取数据构建编码树到内存中,再结合表1~2信息(也存放在内存)进行查询. Table 2 Path Table表2 路径表 Table 3 Time Table表3 时间表 供应链中的典型追溯查询如表4所示,大致可分为3类:追踪查询如Q1、面向路径查询Q2和Q3、聚合查询Q4~Q6,下面对其做具体说明. Table 4 Query Classification Table表4 查询分类表 1) 追踪查询 查询某标签的历史路径,包含访问过的每个位置及进出时间.首先,在表1中找到对应的PathID,通过PathID确定末尾结点的码值,然后从根结点出发,根据子亲代判定定理查出整条路径,详见算法2.从算法2中我们可以看出,追踪查询效率的高低关键在于子亲代判断速度的快慢. 算法2.追踪查询. 输入:标签号TagID、编码树的根结点root; 输出:TagID所经过的路径P. ① 在标签表中找到TagID对应的PathID; ② 在路径表中找到PathID对应的编码code; ③ for (i=0;root.child[i]的编码!=code; i++) ④ ifcode与root.child[i]满足子亲代判定 ⑤ 将root.child[i]存入P; ⑥root=root.child[i]; ⑦ end if ⑧ end for ⑨ ifP≠∅ ⑩ 将code代表的结点存入P; 2) 不含时间的面向路径查询 查询访问过某位置的标签集合.此查询需先确定位置信息匹配的结点,再根据结点找到路径和标签号,详见算法3. 算法3.面向路径查询(不含时间). 输入:位置loc、编码树的根结点root; 输出:查询到的标签集合T. ① 从root遍历树: ② if 结点曾访问过loc ③ 将结点的编码存进codelist中; ④ end if ⑤ 遍历路径表,找到PathID对应的code: ⑥ ifcode在codelist里 ⑦ 将对应的PathID存进Plist中; ⑧ end if ⑨ 遍历标签表,对TagID对应的PathID: ⑩ ifPathID在Plist里: 从算法3可知,面向路径的查询牵涉到多张表的完全遍历,因此较于追踪查询开销较大.其次,面向路径的查询效率同样与子亲代关系判断速度有关,且因查询的只是位置信息,所以也与编码信息有关. 3) 含时间的面向路径查询 与算法3类似,在输入时增加进入时间和离开时间约束,在算法3的行②增加时间约束即可.因增加了约束,查询时比较次数会提高,开销增大.同时因查询的不是单一信息,而是时空信息,单独编码位置的方法会不适用. 4) 聚合查询 聚合查询是比前3类查询更为复杂的查询,其查询的条件比较多,且通常需要在查询结果的基础上添加聚合函数. 算法4.聚合查询. 输入:编码树的根结点root、查询条件condi、聚合函数aggfunc; 输出:最后的查询结果Q. ① 从root遍历树: ② if 结点满足查询条件condi ③ 搜索相关表,查询结点对应的记录; ④ 将记录存进Qlist中; ⑤ end if ⑥Q=aggfunc(Qlist); ⑦ 返回Q. 本实验将从2个方面进行实验. 1) 将所提出的偏增向量编码及优化策略OAVC,OOAVC与3种近年来RFID路径编码方法对时空数据进行编码,比较查询开销、更新开销、初始编码时间开销、最大编码值等.选用的对比编码策略为: ① 区间编码(region coding, RC).该编码利用先序遍历的方法,给每一个结点分配2个值,从根结点出发编码第1个值,编码孩子结点后回到孩子结点编码第2个值.2个码值如同区间的左右,若有结点的码值在区间范围内,则为其孩子结点. ② 素数编码(prime coding, PC).该编码给每个结点分配唯一的素数,利用素数积因式分解唯一性进行子亲代判断. ③ 复合编码(composite coding, CC).该编码利用区间编码对时空数据结点进行编码,同时针对位置信息单独再用素数编码建立不含时间的位置路径树.对不同查询,灵活运用2棵树信息进行查询. 2) 比较OAVC和OOAVC的最大编码值,分析优化效果. 本实验的数据集通过仿真实验产生.我们构造一棵深度为M的满N叉树,将时空数据结点作为树的结点,并按一定规律随机赋值,在位置信息上允许路径有重复的位置出现,即位置信息有环路.其中:M表示树的层数(虚结点的孩子结点为第1层),其含义为路径长度的最大值,用来控制树的深度;N代表每个结点的孩子数,以控制树的宽度. 为分析树的深度、宽度对不同编码的影响,我们分别生成数据集D1~D6,如表5~6所示.其中,数据集D1~D3是固定N=5,只增加树的深度(即3~5)生成;数据集D4~D6是固定M=4,只增加树的宽度(即6~8)生成. Table 5 Dataset Increases by the Depth of the Tree表5 数据集深度递增 Fig.8 Query overhead on the D1~D6图8 不同编码在数据集D1~D6上的查询开销 Table 6 Dataset Increases by the Width of the Tree DatasetMNumber of NodesNumber of RecordsND441555528186D5428011059317D6446811520918 1) 查询开销 我们对表4中每种查询随机生成查询条件,在数据集D1~D6中分别重复实验,计算平均时间,作为查询开销的评价指标. 图8为各种编码策略在数据集D1~D6中各类查询的时耗图,其中横坐标为数据集类别,纵坐标为平均查询时耗. 对于Q1而言,OOAVC和OAVC在判断子亲代关系时,由于一个编码有4个值要比较,因此会略慢,但与其他编码相差不大. 对于Q2,除复合编码外,OOAVC和OAVC与其他编码大致相同.而对于复合编码,尽管其额外编码了位置信息,相当于降低了搜索范围,本应在此类查询上占据优势,但本实验数据集在位置上存在环路,一个位置可能对应多个编码,导致在解码时要遍历整张表,此外编码与位置对应的表存在外存中,因此整体上表现最差,这也体现出环路问题会使只考虑位置信息编码变得更为复杂. 对于Q3而言,查询包含时间和空间信息,此时所有编码的编码对象都为时空数据结点,开销主要影响因素为子亲代判断速度,OOAVC和OAVC尽管子亲代判断过程稍复杂,但查询速度与其他编码相差不大.可以发现,Q3整体开销略高于Q2,这是因为每次查询要多比较时间信息,从而开销增大. 对于聚合查询Q4,Q5涉及到时间信息,因此各编码整体上与Q3结果类似,而Q6只涉及空间信息,结果与Q2类似. 综合各类查询上来看,素数编码的效率最高,而OOAVC与OAVC尽管不占优势,但差距并不大,能支持和满足大多数查询. 2) 更新开销 同样地,我们随机选取树中的某个结点,插入1个叶子结点作为其孩子并进行编码,在数据集D1~D6中分别重复操作,计算平均更新开销作为评价指标,结果如图9所示: Fig.9 Comparison of update cost of each encoding on D1~D6图9 各编码在数据集D1~D6上更新开销比较 由图9可看到,相比于区间、素数、复合编码,所提出的2种偏增向量编码更新开销几乎为零.区间编码是因为编码码值都连续,没有空位留给新插入的结点,1个结点的插入会导致大面积结点需要重新编码.素数编码是因为当编码到一定大小时,搜索新的素数也需要花费时间,因此效率也偏低.复合编码在查询时继承了2个编码缺陷,更新开销最大. 3) 初始编码时间开销 初始编码时间开销是指给定一棵树结构,对其每个结点进行编码所需要的时间.同样,我们在数据集D1~D6中统计编码平均时间作为评价指标,得到图10所示: Fig.10 Comparison of initial cost of each encoding on D1~D6图10 各编码在数据集D1~D6上初始编码开销比较 可以发现,OOAVC与OAVC的初始编码开销均较大程度优于其余策略.在数据集较小的情况如D1,D2,D4,区间编码的开销是要大于素数编码的,但当数据集变大时,搜索新素数导致素数编码开销更大.同时,复合编码由于有2棵树需要编码,开销最大. 4) 最大编码值 最大编码值即为路径编码的最大值.对于OOAVC,OAVC,RC而言,路径编码用路径中叶子结点的编码来表示,最大编码值即为结点编码的最大值;对于PC,CC而言,路径编码由根结点到最后一个叶子结点编码的乘积得到. 表2中存储了每条路径的路径编码,可直接从表2中找到最大的码值.由于不同编码的码值差距过大,我们用编码值的lb对数表示,结果如图11所示. 由图11我们可以看到,素数和复合编码的最大编码值已经远远超过了其他编码的码值.理论上,复合编码的最大码值应小于等于素数编码,这取决于位置信息相同的路径多少,而从图11中看出,两者最大编码值相差并不大,说明都存在严重的溢出问题. 而通过观察对比,在更深的树如数据集D3上,最大码值会比更宽的树如数据集D5上更大,这也与素数的乘积增长极快相吻合.事实上,再在数据集D3上继续提高深度或宽度,都已经会导致超出所定义的数据结构,导致溢出错误. Fig.11 Maximum coded value of each encoding in dataset D1~D6图11 各编码在数据集D1~D6上最大编码值 5) 码值优化比较 为了更清晰地观测不同编码的码值,我们将各类编码具体的码值表给出,如表7所示.我们可以发现,尽管同素数相比,向量编码的码值较小,但与区间编码相比码值增长同样十分迅速,因此对OAVC的码值进行优化是十分有必要的,可以发现,OOAVC码值得到了一定减少,而当数据集逐渐变大时,优化的效果也更明显. 同时,表7中素数编码与复合编码的最大编码值相差有限,说明溢出问题仍是复合编码的难点,而相较于复合编码的最大编码值,无论是OOAVC还是OAVC都要小得多. 综合实验结果,我们将各编码策略整体表现归纳如表8所示. Table 7 Table of Maximum Encoding Values表7 最大编码值表 Table 8 Comparison of Comprehensive Performance of Each Code表8 各编码综合性能比较 可以看出,所提出的偏增向量编码能较好地满足各类追溯查询要求,具有编码速度较快、码值溢出较为缓慢、更新效率高且支持环路的特点,因此是一种效率较高且具有强鲁棒性的编码策略. 本文根据基于RFID供应链环境中标签对象路径追溯查询需求,提出了一种能支持环路、实时更新的偏增向量编码策略.同时,对该编码潜在的码值溢出问题提出了优化方法,并对其正确性进行了证明.在模拟数据集上完成了实验,结果表明:所提出的编码策略能基本满足大多数查询需求,且具有健壮、强鲁棒的特点,能较好地适应供应链复杂环境. 目前,已有编码策略大多仅在集中式环境下使用,下一步拟研究分布式供应链向量编码策略.
3 路径追溯查询
3.1 存储模式



3.2 追溯查询实现

4 编码实验与结果分析
4.1 实验目的
4.2 数据集

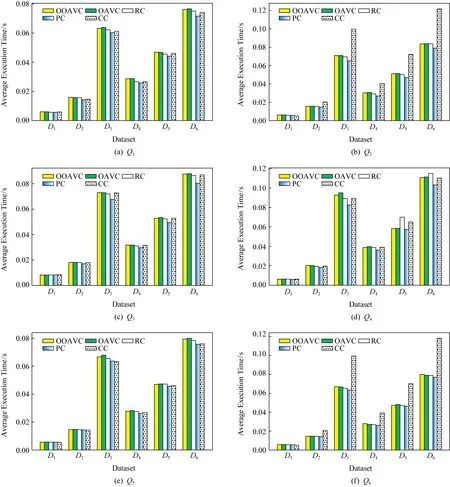
表6 数据集宽度递增
4.3 结果分析




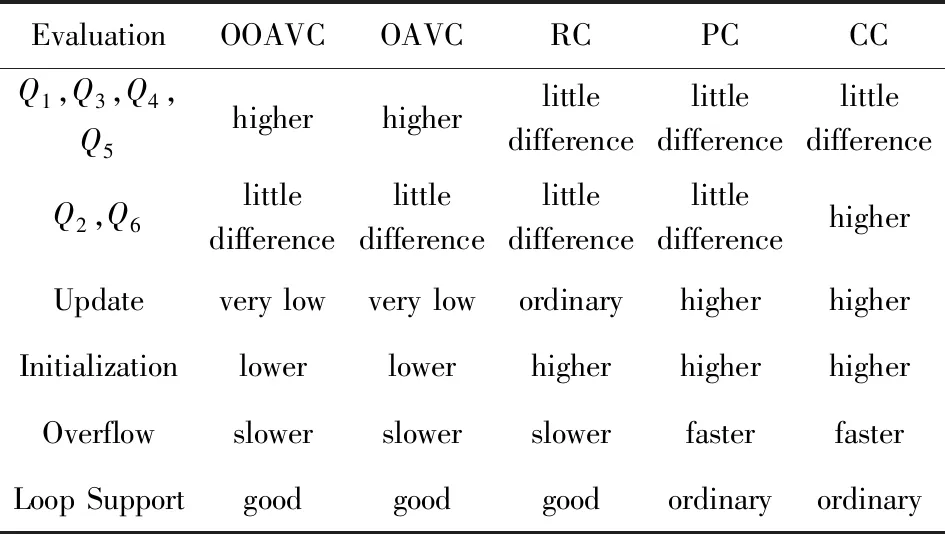
5 总结及展望

