RGNE:粗糙粒化的网络嵌入式重叠社区发现方法
赵 霞 张泽华 张晨威 李 娴
1(太原理工大学信息与计算机学院 太原 030024)2(伊利诺伊大学芝加哥分校计算机科学学院 美国芝加哥 60607)
互联网技术的快速演进,社交网络已成为大数据时代的重要载体.通过社区结构对网络进行描述,可简化对整个网络的功能、交互及其演化的研究.社区发现有助于更深地了解网络的本质,获取推荐信息、预测网络的演化等.社区发现的目标是利用网络拓扑结构信息或者网络节点的属性信息,从复杂的网络中获得模块化的社区结构.社区发现旨在探测复杂社交网络中具有共性特征或紧密关系的群体,例如有相同的爱好、属于同一个研究领域等.目前它在社会学、生物医学和计算机科学等领域都有广泛应用[1].
社区发现研究已有众多工作,主要方法有:1)基于模块度优化的方法,主要思想是优化模块度Q值[2].如Newman等人[3]提出的GN算法,它虽然结果较为精确但是计算复杂度太高.2)基于谱分析的社区发现算法,例如Shi等人[4]提出的方法结合一种经典的计算特征值的方法来进行局部社区发现.这类算法多通过将节点对应的矩阵特征分量视为空间坐标,从而可将网络节点映射到多维向量空间,再采用传统的聚类算法将它们聚集成社团.但由于需要计算矩阵的特征值,通常计算开销很大.3)基于标签传播的算法(label propagation algorithm, LPA)[5-6],这类算法时间复杂度低、收敛速度快,但易受随机游走的影响,划分结果不稳定.4)基于聚类的社区发现方法,它的基本思想是在网络中增加或是删除边[7].以上这些硬划分方法都有一个前提条件,就是要保证社区是易分离的,每个元素都可被划分到某个社区.然而现实中复杂网络存在大量不确定因素,如数据含有噪声、节点属性不完备等,这也导致一些节点属于多个社区形成重叠社区[8-9],使用硬划分可能会造成划分冲突现象.如何利用这些不确定性信息挖掘更加精确的社区结构成为一大挑战.
针对社区边界不确定社区漂移的情况,张泽华等人[10]提出了基于邻域粗糙化的社区局部扩张方法,通过给出的结构稳定性度量进行局部扩张生成重叠社区.本文则进一步考虑融合多源信息解决不确定网络中的社区发现问题.由于社区发现的结果很大程度会受到节点间距离测度的影响,对于复杂空间中分布的数据使用传统的距离测度方法难以取得较好的效果.为了得到良好的社区发现结果,节点对之间的相似性度量起重要的作用.直观认知若2个节点相似,则很可能会有共同或类似的邻居节点.而本文采用网络嵌入方法获得的节点表示有效融合了网络的结构和属性信息,可以更好地描述节点结构和节点间的相似性.但由于现实不确定性的广泛存在,噪声数据、节点属性或结构不完整,均会导致难以进行社区发现或是得到的社区结构不准确.
因此,本文提出了粗糙粒化的网络嵌入(network embedding based on rough granulation, RGNE)方法进行社区发现.首先,使用网络嵌入将网络节点映射到一个低维连续的特征向量空间,同时还能保持网络的拓扑结构和节点内容信息,这样考虑到了多层次的信息以便于对社区结构进行更有意义的理解.然后,结合粗糙粒化的方法来处理社区中不确定性区域.最后生成重叠社区.
本文的主要贡献包括3个方面:
1) 提出了融合多源信息解决不确定网络的社区发现方法RGNE,该方法采用网络嵌入方法来表示节点,同时考虑了网络拓扑和节点属性等多种信息.
2) 为了解决含有不确定信息的重叠社区发现问题,通过将传统的聚类方法与粗糙粒化方法结合来准确地处理网络不确定区域.
3) 在公开数据集上与传统的社区发现算法相比,RGNE方法的有效性明显提升,并且对主要参数进行讨论;在人工数据集上本文算法显示出分析较大规模网络的优势.
1 相关工作
1.1 网络嵌入
复杂的信息网络可以看做是由顶点和边(链接)构成的有向或是无向图,其中可能包含数十亿的顶点和边,在这样的网络上进行推理和分析会非常困难.因此合理地对网络进行表示学习变得尤为重要.网络嵌入方法(network embedding)[11]通过将网络节点映射到一个连续低维的特征空间中,得到的节点表示有利于后续的机器学习任务如社区发现、分类、链路预测、可视化等[12].近年来网络嵌入的研究如火如荼.早期的降维算法SVD(singular value decomposition)[13]是将所定义的矩阵压缩为一个较小的矩阵,但是这样的方法只能用于线性结构的数据;后来受到深度学习的启发,基于词向量模型的表示学习算法相继被提出.最有代表性的是Perozzi等人[14]提出DeepWalk算法,该算法采用SkipGram模型[15]来学习节点嵌入,克服了网络稀疏性问题;由于DeepWalk只适用于无权网络,Tang等人[16]提出适用于多种类型网络的LINE模型,通过一阶相似性和二阶相似性来捕捉网络局部和全局结构;Le等人[17]提出了一种半监督的模型Doc2Vec,该模型利用了丰富的文本信息来对词向量和文档向量建模,对文本信息丰富的网络具有较好的效果.然而,这些基于DeepWalk的改进模型或是只利用了网络的结构信息,或是只利用了属性信息,无法全面地表示整个网络.所以,Pan等人[18]提出了将DeepWalk和Doc2Vec结合的TriDNR模型,该模型使用网络结构信息、节点内容信息和标签信息来对节点进行表示.为了捕获高度非线性的网络结构,Wang等人[19]提出了一种半监督的深度模型SDNE,该模型通过一组非线性函数来优化一阶相似性和二阶相似性,能将数据映射到高度非线性的空间.
从上述方法看来,现有网络嵌入方法多仅利用单一的信息,但是结合多种信息源对网络能有更加精准的描述,所以本文核心工作就是利用多源信息对网络节点进行建模.
1.2 粗糙集理论
1982年由波兰数学家Pawlak[20]提出的粗糙集理论是粒计算的一大支撑理论.它将概念粒子用集合来表示,不同粒度的粒子可视为对集合的划分.作为一种被广泛使用的智能计算方法,粗糙集理论能够很好地处理不确定性问题,目前已经被广泛应用到分类决策、知识发现、人工智能等领域[21-25].
人类认识事物的过程就是对事物的理解从不确定到确定的过程,不确定是客观事物在发展过程中表现出的随机性和模糊性等基本特征[26].从粗糙集理论看,在某种信息粒度层面上,确定性和不确定性存在相互转化的关系,而且在不确定现象中还隐藏着一些重要的规律.所以研究如何表示不确定问题并从中获得某些确定的规律,并且通过计算机建立模型来模拟认知过程尤为重要.由于粗糙集可以有效处理信息不完备的情况,所以本文选择用它来发掘不确定性数据中隐藏的相关性,获得不确定知识的表达.有关粗糙集的一些基本定义为:
定义1.等价类.设W是非空集合,R是等价关系.对于w∈W,节点w的R等价类定义为[20]
[w]R={x|x∈W,(w,x)∈R},
(1)
(2)
W/R={[w1]R,[w2]R,…,[wN]R},
(3)
其中,N是等价类个数,且当i≠1时,[wi]R∩[wj]R=∅,W/R是集合W的等价划分.
定义2.对于集合O⊂W的上近似集U(O)、下近似集L(O)和边界域B(O)的定义为[20]
U(O)={w|w⊂W,[w]R∩O≠∅},
(4)
L(O)={w|w⊂W,[w]R⊂O},
(5)
B(O)=U(O)-L(O),
(6)
显然,它们有∅⊆L(O)⊆O⊆U(O)的关系.
2 粗糙粒化的网络嵌入社区发现方法
粗糙粒化的网络嵌入社区发现方法RGNE的主要思想是先通过随机游走得到网络G(无向无权)的结构信息和属性信息,然后结合这2部分信息得到每个节点的低维向量表示;根据粗糙集理论处理不确定区域,将社区划分为上近似集区域和下近似集区域,再通过定义的距离度量将节点划分到近似集中,迭代至收敛得到最后的社区发现结果,方法主要步骤如图1所示.

Fig.1 The schematic illustration of RGNE图1 RGNE方法示意图
2.1 获得节点表示
网络嵌入的目的是将节点嵌入到低维的空间中,而且能够保留节点之间的关系,可以通过局部信息或是全局信息来捕获节点间的关系.节点相对于其他节点的相似性称之为上下文信息,从网络结构信息获得的上下文称为结构上下文,从节点属性信息而来的称为属性上下文.在网络嵌入的阶段主要包括3个步骤:网络生成、随机游走和学习节点表示,如算法1所示:
算法1.网络嵌入算法.
输入:网络G=(V,E)的邻接表;
参数:步长ηs和ηa、步数φs和φa、窗口大小t、嵌入维度D;
输出:节点的向量表示Ω、出现频率最多的前K个节点.
步骤1.从G中获得结构图Gs和属性图Ga.
步骤2.对于V∈Vs∪Va,初始化所有节点向量Ω(V).
步骤3.在结构图上进行随机游走,
Ws=RandomWalk(Gs,Vs,ηs,φs).
步骤4.在属性图上进行随机游走,
Wa=RandomWalk(Ga,Va,ηa,φa).
步骤5.Ω=SkipGram(Ws,Wa,t)结合式(7)~(9)学习节点的最终嵌入表示.
步骤6.返回节点表示Ω.
2.1.1 网络生成
在网络生成阶段,将原始的网络G=(V,E)分为结构图Gs=(Vs,E)和属性图Ga=(Va,A,Ea).其中Ga是一个二部图,结构节点Vs∈V,内容节点Va∈V,A是属性节点,Ea是属性节点和内容节点的边.内容节点之间的路径包含属性节点,形成了属性上下文.
2.1.2 随机游走
在随机游走阶段,通过短随机游走同时获得结构上下文和属性上下文,短随机游走已经被证明可以获得较高相似度的节点上下文[14].在Gs上的随机游走捕获了结构上下文信息,对于每个节点都进行步长为ηs的φs步随机游走并构建节点库S,si为随机游走序列(节点库S)中的第i个节点;在Ga上的随机游走,更关注内容节点共同出现的频率,因此忽略了属性节点A,而且根据经验所得,相似的节点会有更大的概率在随机游走中一起出现,同理,对每个内容节点都进行步长为ηa的φa步随机游走并建立节点库C,cj为随机游走序列(节点库C)中的第j个节点.
2.1.3 节点嵌入学习
在节点嵌入阶段,借助语言建模Word2vec[27]中的Skip-Gram模型来学习节点的向量表示.由于Skip-Gram是用单词预测上下文的模型,通过将窗口内单词之间的共现概率最大化来学习向量表示.所以借鉴这个模型,将网络节点当作语言模型中的单词,随机游走得到的节点序列当作语言模型中的句子作为Skip-Gram的输入,输出的可以是结构节点、属性节点亦或是两者的共同节点.
利用结构上下文的嵌入学习过程为
(7)
其中,m≠i,t为窗口大小,p(sm|si)表示当中心节点是si时第m个节点在上下文中出现的概率,它衡量了节点间的相似度.
利用属性上下文的嵌入学习过程为
(8)
其中,n≠j,p(cn|cj)表示当中心节点是cj时第n个节点在上下文中出现的概率.
给定一个目标节点,假设节点的上下文节点相互独立[11].本文的目标是最大化结构上下文和属性上下文的概率,所以目标函数为
L=Ls+Lc.
(9)
计算目标函数的难点在于计算p(sm|si)和p(cn|cj),本文选择使用Softmax来近似地计算这2个条件概率:
(10)
其中,γ(·)表示上下文节点,Ω(·)表示目标节点.同理可以计算出p(cn|cj).
2.2 粗糙粒化的社区发现
传统的社区发现方法一般将社区内的所有节点“一视同仁”.对于一些处在不确定性区域的节点,如果使用硬划分方法很可能会产生局部冲突.如图2所示,节点被划分为2个社区Z1和Z2,节点4和9分别是2个社区的中心,对于节点6根据现有的认识无法准确判断出它属于哪一个社区.所以本文提出了结合粗糙集理论的社区发现算法来解决这样的问题,该方法将社区Z分为上近似社区U(Z)和下近似社区L(Z),其中U(Z)包括核心节点和边缘节点,L(Z)只包含核心节点,而社区的边界B(Z)包含属于U(Z)不属于L(Z)的节点(如图3所示),这样就可以描述社区的不确定性区域.算法的主要步骤由算法2给出.

Fig.2 Community drift图2 社区漂移

Fig.3 Rough community description图3 粗糙社区描述
2.2.1 社区中心
社区发现任务中准确找出中心节点Z*是一个非常重要的任务,找出正确的中心节点对社区发现来说事半功倍,错误的中心节点会导致算法收敛速度降低,甚至会得到错误的社区结果.在对社区进行初始化时,先将网络嵌后获得的前K个出现频率最高的节点作为初始中心节点,由于K值需要预先指定,本文将在实验部分讨论K值对最后的社区发现效果产生的影响.


(11)
其中,|L(Zk)|表示社区Zk下近似集包含的节点数,|B(Zk)|表示边界域的节点数.θL和θB分别是对应近似域的加权参数,且θL+θB=1.
认识来源于实践,反过来又为实践服务。高效节水灌溉一时的挫折或失败,是人们在实践中还没有充分认识到其技术和条件适应性的结果,这些问题会随着人们的认识水平不断提高而得到解决,因此必须要勇于实践,不断从实践中提高认识水平,又反过来进一步指导新的灌溉实践。
2.2.2 社区划分
通过判断节点与社区中心节点的关系,可以得出节点与社区的关系,从而将其划分到社区的近似集中.根据粗糙集理论,节点与社区的近似集之间的关系满足3个性质[28]:1)一个节点只能属于一个社区的下近似集;2)如果节点属于一个社区Z的下近似集,那么这个节点也同样属于社区Z的上近似集;3)如果节点不属于任何社区的下近似集,那么它一定属于2个或更多社区的上近似集.
首先,对每个节点向量分别计算它们与各个社区中心节点的距离d(v,Z*)和距离最近中心节点的最小距离dmin.对于节点与社区中心节点距离的计算用到了欧氏距离,欧氏距离也称欧几里得距离,是最常见的距离度量,衡量的是多维空间中2个点之间的绝对距离.关于节点与第k个社区的中心节点距离计算为
(12)
其中,N为节点个数.用d(v,Z*i)/d(v,Z*j)来表示节点和2个社区的关系,其中1≤i,j≤K,且i≠j.然后通过节点与社区近似集之间的3条性质,得出节点与各个社区的关系.引入参数δ,0<δ≤1,当dmin/d(v,Z*)≥δ时,表示该节点属于对应中心节点和距离最近社区的上近似集中,否则节点将属于距离最近社区的上下近似集中.值得注意的是,参数δ的大小表示了社区边界域的大小,随着δ的减小,边界区域将包含更多的节点.实验中设置δ=0.8.
算法2.社区发现算法.
输入:网络节点向量表示Ω、社区个数K;
输出:社区集合Z={Z1,Z2,…,ZK}.
步骤1.将算法1得出的出现频率最多的前K个节点作为初始中心节点;
步骤3.根据dmin/d(v,Z*)≥δ,计算节点与社区中心的距离,并将其划分到相应的近似集中;
步骤4.根据社区近似集更新中心节点,
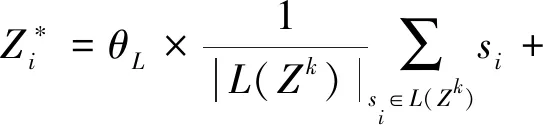
步骤5.返回社区结果Z.
3 实验与分析
在不同规模的数据集上分别与4个适用于社区发现的算法进行对比,验证算法RGNE的有效性并且对参数设置进行讨论.又在人工数据集上分析网络规模和网络度分布对社区划分结果的影响.
3.1 评测数据集
本文使用公开数据集中的DBLP数据集是从4个研究领域的34个会议中提取的参考书目数据.将数据集中的作者作为节点,选取了60 744个节点,论文标题作为节点内容,将数据集中出现频率3次以上的词作为节点属性.另外2个公开数据集是Zachary Karate Club和College Football Network.其中,Zachary Karate Club是一个空手道俱乐部的成员关系网络,共有34个成员和以管理员和教练为中心的2个小组;而College Football Network是2000年美国大学足球橄榄球联盟比赛网络,115支队伍被分为12个联盟进行比赛.数据基本情况如表1所示:

Table 1 Datasets Statistics表1 测试数据集
此外,使用LFR合成人工数据集[29],用于有向、加权或重叠社区实验评测.LFR数据集可通过参数控制人工社区的度分布和社区大小,通过增加网络节点个数和改变网络度分布来分别分析网络规模和社区边比率大小对本文算法的效果影响.其中,涉及到的控制参数有:网络规模N、混合参数λ(社区内的边与其他社区边的平均比率).
3.2 实验设置
在节点表示阶段进行的随机游走过程中,设置步数φs和φa分别为10,步长ηs和ηa分别为80,Skip-Gram模型的窗口大小t=5,节点表示的维度D=128.在社区发现的阶段,将下近似集和边界域的权重设置为θL=θB=0.5.
3.3 评价指标和对比方法
本文使用评价社区发现算法效果常用的标准化互信息(normalized mutual information,NMI)[30]和模块度Q值作为标准,分别为式(13)(14).
给定2个划分结果X和Y,M为混淆矩阵,Mij是属于结果X的社区i和结果Y的社区j的节点数.
(13)
其中,MX是X的社区数,MY是Y的社区数,N为节点数.NMI用来衡量2个结果的相似度,取值范围是[0,1],数值越大代表社区发现的结果越好.
(14)
其中,i为所属社区号,K是社区总数,li是社区i的总边数,di是社区i节点的总度数,m是整个网络的总边数.Q值越大说明社区划分效果越好,取值范围是[-0.5,1],当Q值在0.3~0.7之间时,说明社区发现的效果良好.
通过与4个社区发现的典型算法对比,对本文提出的RGNE算法性能进行评估.
1) LPA[5].基于标签传播的社区发现算法,该算法为所有节点指定一个标签,通过标签传递和更新.算法计算复杂度较低,易于快速收敛.
2) GN[3].算法定义一条边的介数为网络中所有节点之间的最短路径中通过这条边的数量,而介数高的边要比介数低的边更可能是社区之间的边.每次都删除网络中介数最大的边,直至网络中的所有边都被删除.
3) Louvain[31].一个基于多层次优化的启发式算法.该算法的主要思想是将每个节点划分到相邻节点的社区中使得模块度Q值不断增大,直到Q值不再变化,此时再根据生成的社区结构重构网络.
4) DeepWalk[14].利用网络结构中随机游走序列的信息来代替语言建模中的句子,将节点向量映射到一个低维稠密的空间中.对节点序列用SkipGram模型进行网络节点的表示学习与预测.Node2Vec[32]则采用了不同的随机游走策略,通过定义参数p和q,同时考虑局部和宏观的信息分别进行广度优先和深度优先搜索,其结果较依赖于参数的优化过程.
3.4 实验结果分析
在3.1节中公开数据集上进行实验,并与其他4种算法作比较验证RGNE算法的有效性,所有方法均采用网络嵌入方法得到节点的表示.由图4和图5可得,LPA的较差,因为该算法比较依赖初始中心节点的选取,随机性很大.算法GN表现良好,但是由于要遍历网络中所有的边,所以时间复杂度较高,只适用于小规模网络.Louvain采用层次凝聚的方式对网络进行聚类,它的优点在于能够体现网络的不同粒度的层次结构,易于理解和计算较便捷.但值得注意的是,不同节点上的遍历顺序对结果有一定扰动,在一定程度上会影响计算时间.此外,由于Q函数的约束,GN和Louvain算法都倾向于发现规模相似的网络,对稀疏网络效果一般.DeepWalk略优于2种传统的社区发现算法,但它只利用了网络的拓扑结构忽略了属性信息,所以节点表示不够全面.
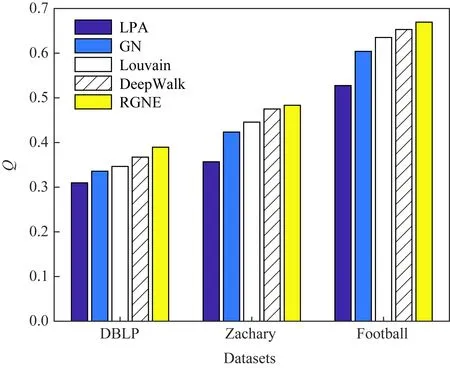
Fig.4 Comparison of Q on three datasets图4 3个数据集下各算法的Q值对比

Fig.5 Comparison of NMI on three datasets图5 3个数据集下各算法的NMI对比
综上所述,RGNE算法效果普遍优于其他算法,在DBLP这样的大规模数据集上更加突出.相较于传统的社区发现算法,RGNE在处理较为稀疏的网络方面具有更大的优势;相较于同样是网络嵌入方法的DeepWalk来说,RGNE能同时利用节点的结构信息和属性信息,所以社区发现效果更好.而且利用粗糙粒化的社区描述对网络不确定区域的节点处理更符合实际社区分布.

Fig.6 Impact of network size on community detection图6 网络规模对社区发现的影响
在人工数据集上,通过增加网络节点和边的数量来生成更为复杂的网络,以此来验证各个算法的可扩展性.设置混合参数λ为实验最优值0.3,将网络规模由2.5万个节点递增到10万个节点.图6则表明,随着网络规模的增大,各种算法的NMI值出现了不同程度的下降,网络嵌入方法的性能显然较优,其他的算法由于计算复杂度较高,网络规模倍增时算法受影响较大,RGNE算法表现出良好的稳定性.
继续在人工数据集上进行实验,首先固定网络大小为1 000个节点,然后改变混合参数λ的大小,λ∈[0,1].图7显示了在不同λ值下各算法的NMI值变化.所有算法均在λ增加的情况下,即社区结构不清晰时NMI值逐渐降低.对于较小的λ,所有算法的差别不是很大,但是当λ≥0.3时,RGNE算法显示出优势,很明显地曲线下降趋势缓和,而其他算法在λ增加至某一值时NMI值降为0,原因是本文的方法可以有效融合网络的结构信息和属性信息而且同时能正确处理不确定信息.

Fig.7 Effect of λ on NMI图7 混合参数λ对NMI的影响
3.5 参数讨论
由于预先指定了社区中心个数K,确定合适的K值会对最后的社区发现效果产生很大影响,采用手肘法来确定K值,评估指标是误差平方和E[33].它的核心思想是:随着划分数K值的增大,划分变得更加精细,每个社区内的聚合度增加,E值会减小;当K小于真实划分数时,K值增大会使每个社区内聚合度增加,所以E的降幅增大;当K值达到真实划分数后,再增大K值聚合度不会有很大改变,所以E降幅减缓趋于平缓.
(15)
其中,v是社区Zk中选取的样本节点,Z*是Zk的中心,K越大,E越小,样本的聚合程度越高.在Zachary和Football这2个数据集上对K值进行讨论.
由图8可得,在达到真实的社区数前,E的降幅较大,因为划分得更精细会使社区内的聚合度增加;2个数据集分别在K=2和K=12时到达真实划分数,之后曲线的降幅骤减,此时再增加K值的回报很小.
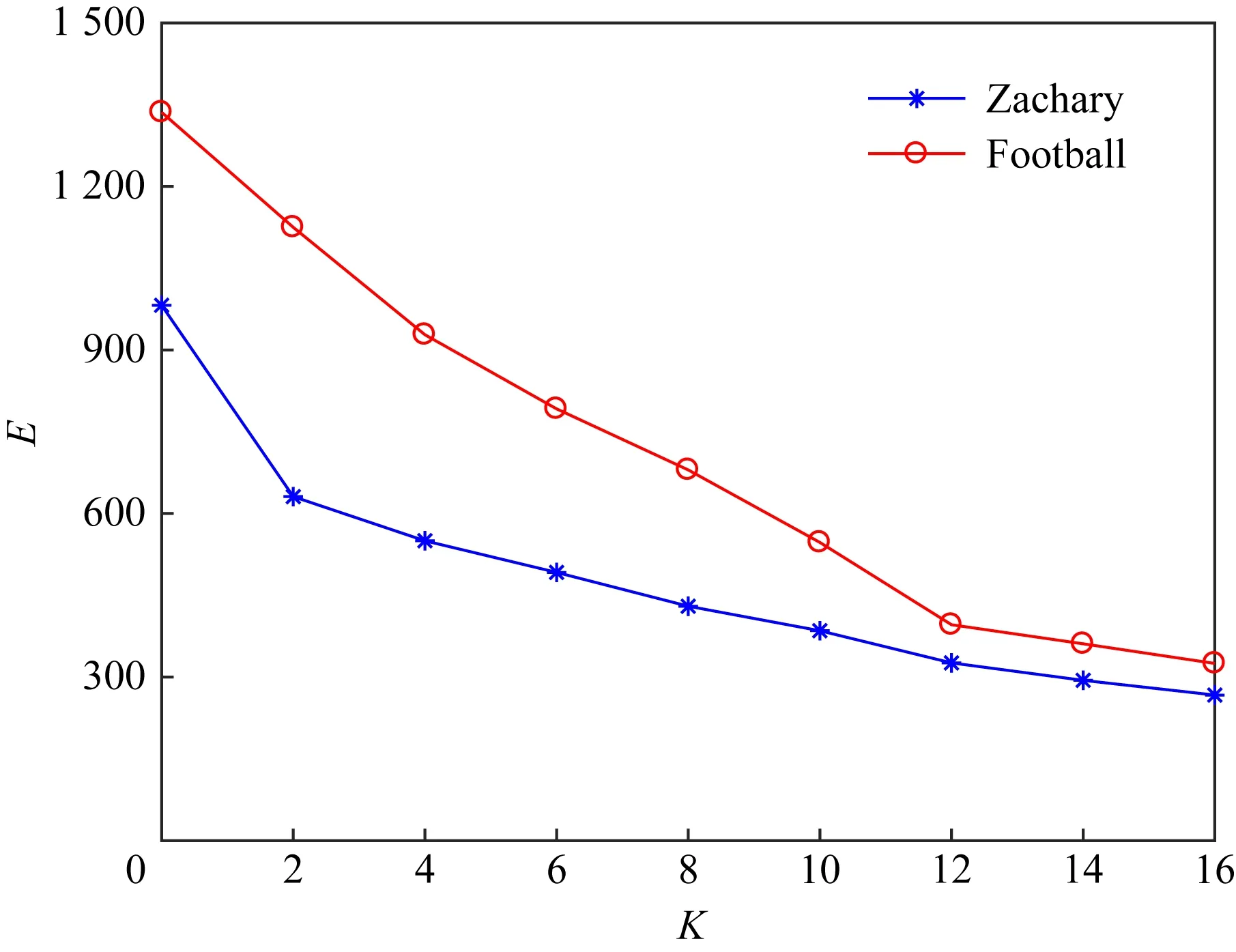
Fig.8 K analysis on two datasets图8 在2种数据集上的K值分析
此外,社区发现算法中的参数δ对社区发现结果会有一定的影响,为了更好地了解造成的影响,本文在DBLP数据集上进行参数分析.由于δ的值代表社区边界区域的大小,随着δ的减小,边界区域将包含更多的节点,此时社区发现的难度也会增大.选择在区间[0.5,1.0]内讨论参数影响.
由图9可得,在参数δ=0.8时5种算法均能取得最好的效果.这是因为当δ过小或是过大,即社区边界域太大或太小都不利于社区发现.当边界域较大时社区包含更多不确定性的节点,社区发现的困难增大,此时结合粗糙集理论的RGNE算法明显优于其他算法;当边界域较小时,各个社区之间的边界模糊,社区结构不清晰同样难以得到良好的结果.

Fig.9 Effect of δ on Q图9 参数δ对Q值影响
4 结 论
由于现实中复杂网络存在不确定性数据,使用传统的硬划分方法可能会造成划分冲突.而这些不易划分的元素在社区发现中是不可忽视的,利用这些不确定性元素可以挖掘出更加精确的社区结构.本文提出的RGNE算法先是通过网络嵌入获得融合结构信息和属性信息的节点表示,并且可以将相似的节点映射到距离相近的低维连续的向量空间.然后结合粗糙集理论来处理不确定性信息进行社区发现,从而得到更为精准的社区发现结果.目前本文的研究是在中小型规模的网络上进行,在未来的工作中可以着眼于大规模网络的社区发现.

