即时车辆共乘问题的多策略解空间图搜索算法
郭羽含 张 宇 沈学利 于俊宇
(辽宁工程技术大学软件学院 辽宁葫芦岛 125100)
车辆共乘(ride-sharing),也称车辆合乘,指对一定时空范围内的车主和乘客进行匹配组合和路径规划,以降低车辆空载率,从而提升运输效率、缓解交通拥堵、降低环境污染并节省出行资源.车辆共乘根据车主属性可分为顺风车模式(hitch-mode)和出租车模式(taxi-mode).在顺风车模式中,车主和乘客均指定自身所在地和目的地,需最大化车主乘客对的匹配价值之和.而在出租车模式中,车主以运输乘客赚取利润为目的,即只有当前所在地而无自身目的地,该种模式下仅需最小化车主所在地与乘客所在地间的低效能路程.即时车辆共乘则指车主和乘客在发布出行信息后即时出发,需尽可能最小化其等待时间,因此需在相对较短时间内生成车主乘客匹配方案,对计算速度有一定敏感性.本文针对顺风车模式的即时车辆共乘进行研究.相对于经典路径规划问题[1-2],国内外对于车辆共乘问题的研究较少,文献[3-4]对本问题进行了综述,将其研究方向主要归纳为问题模型[5-12]和求解算法[13-19]2方面.在问题模型方面,Baldacci等人[5]提出一种最小化总行驶距离的精确算法模型.Ece等人[6]设计了一种最小化总行驶时间的模型.齐观德等人[7]对乘客候车时间进行了模拟和预测.Schilde等人[8]针对时间性和随机性因素对行驶速度的影响提出2套元启发式解决方案.谭家美等人[9]研究了信任水平对动态共乘匹配效果在仿真模型上的影响.Stiglic等人[10]以一种基于会面点的模型来提高匹配方案的效率和灵活性.Ta等人[11]建立了一种最大化共享路程比率的模型.肖强等人[12]基于泊松分布对出租车合乘概率及等待时间进行了模拟.在求解算法方面,Agatz等人[13]提出一种Rolling Horizon策略.Kleiner等人[14]设计了一种基于拍卖机制的激励兼容DRS解决方案.邵增珍等人[15]以一种2阶段聚类启发式优化算法解决该问题.Pelzer等人[16]使用了一种基于分区的动态共乘匹配算法.杨志家等人[17]针对车辆共乘问题设计一种2阶段的分布式估计算法.Alonso-Mora等人[18]构建了一种实时大容量乘坐共享数学模型的约束优化算法.郭会等人[19]提出基于个性化需求的匹配算法.其他一些研究工作则针对更为具体的案例进行了分析以弥补通用模型中的空白,如Calvo等人[20]和Ma等人[21]分别对城市公共交通问题构建了出租车共享系统,Winter等人[22]结合移动地理传感器网络对车辆共乘进行了研究.Amey[23]通过数据驱动的方法在组织级数据规模上估计了车辆共乘的可行性.付瑶等人[24]发现通过城市出行需求量和交通需求聚集度可以确定交通模式是否可以达到稳定状态.
文献中提出的模型在评估匹配质量方面主要使用3个指标之一:1)最小化总行驶距离[5,10,13-16,20,23];2)最小化总行驶时间[6-9,21];3)最大化共享路径比率[11,19].然而,指标1和指标2忽略了车主和乘客间行程的相似性,无法高效利用交通资源,且降低了车主的收入和乘客的满意度.指标3无法控制绕行距离,导致车主额外驾驶路径可能过长,严重降低了实际应用中的可行性.
车辆共乘匹配问题需对所有乘客与车主通过价值函数生成乘客车主对的价值二分图,然后使用二分图最大权匹配算法求出最优匹配方案及匹配后子图权边总和[7].在大型城市的高峰时段,算法需要在短时间内匹配数以万计的车主与乘客,因此对算法的求解效率要求极高.二分图最大权匹配算法时间复杂度较高,因而当算例较大时,该方法的运行时间将成超线性趋势增长.而文献中提出的近似算法也未能较好地解决求解大算例时的效率问题.
本文针对固定时空范围内的即时车辆共乘匹配问题展开研究,提出一种多策略解空间图搜索算法(multi-strategy solution space graph search algorithm).首先在模型层面提出一种约束绕行距离的价值评估方法,然后以一种并行化的价值矩阵生成方案来改进原本低效的生成方法,最后设计多种策略指导算法在解空间图中进行高效搜索.实验结果表明,该算法的求解质量可达最优解的95%以上,且求解效率明显优于实验中对比的其他算法.
本研究的主要贡献有3个方面:
1) 提出了一种基于共享路程比率(shared route percentage, SRP)和绕行距离的价值评估方法.该方法侧重资源利用率的同时兼顾了司机的收益期望.
2) 提出了离散排列问题的解空间图理论,并基于此理论构建了一种多策略搜索算法来解决即时共乘问题,并阐述了其正确性.
3) 基于大量算例进行了实验测试,证明了本算法可以高效求解大型算例并提供高质量的匹配方案.
1 问题建模
1.1 问题形式化
在固定时空范围内,以无向加权全连通图G=P,E表示一个道路网络.其中,顶点集P={pi|i∈[1,nnode]∩}为道路节点集合,其中元素数量为nnode;无向边集合E={(pi,pj)|i∈[1,nnode]∩,j∈[1,nnode]∩,i≠j},其中元素数量为nedge.边(pi,pj)的距离为eij.以集合D={di|i∈[1,m]∩}表示车主集,其中di代表车主i,每个车主具有所在节点ldi和目的节点adi.以集合R={rj|j∈[1,n]∩}表示乘客集,其中rj代表乘客j,每个乘客具有所在节点lrj和目的节点arj.车主和乘客具有身份唯一性,因此D∩R=∅.匹配车主与乘客时,以共享路径比率来评价车主与乘客的匹配价值,定义车主i与乘客j匹配的价值为vij.问题的目标即为求得一种匹配方案,使得所有车主乘客匹配对的价值总和最大.因此,可将本问题的目标函数定义为
(1)
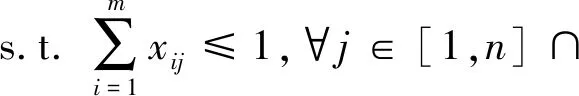
(2)
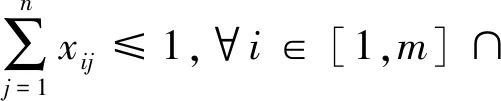
(3)
xij∈{0,1},∀i,j,
(4)
其中,xij表示车主i与乘客j是否匹配,vij表示车主i与乘客j的匹配价值.式(2)~(4)为匹配互斥性约束,式(2)表示每个乘客至多与一个车主匹配,式(3)表示每个车主至多与一个乘客匹配,式(4)限定x取值范围,0表示不匹配,1表示匹配.研究涉及的变量如表1所示:

Table 1 Variables表1 变量表

Continued (Table 1)
1.2 价值评估
本文使用共享路程比率[7](SRP)作为对车主这一主要资源的利用效率的评价标准,并以绕行距离(detour length, DL)对其进行约束,以达到共享效率和方案可行性的平衡.车主与乘客的SRP为乘客的期望路程与车主的总路程的比值.SRP反映出共享资源的利用效率.乘客的期望路程是共享的、高价值的,而车主独自行驶的路程是非共享的、低价值的,因此,该值越大则表示车主的低价值路程相对越短,共享资源利用效率越高,反之则表示车主把大量路程浪费在共享路程之外,对共享资源的利用效率低下.
设有车主dj和乘客存在于道路图G中,则该车主与乘客的共享路程比率为
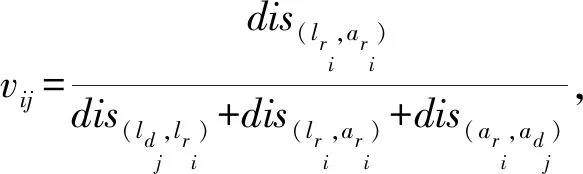
(5)

(6)
lri≠ari,
(7)
ldi≠adi,
(8)
CDL=dis(ldj,lri)+dis(lri,ari)+dis(ari,adj)-
dis(ldj,adj),CDL≤μ×dis(lri,ari),
(9)
其中,dis表示2点之间的路径长度,l表示车主或乘客的所在节点,a表示车主或乘客的目标节点,p表示节点,μ表示车主的利润率.式(6)约束了图的边必定是非负边.式(7)(8)为起点终点互斥性约束,一个车主或乘客的起点和终点应是不同的.式(9)表示车辆的绕行距离及约束,其中CDL表示车主的绕行距离,μ为车主载乘客行驶每公里的收益与车主行驶每公里的花费之比率,式(9)能够约束车主的共享过程处于收益状态之内.
2 多策略单步移动解空间图搜索算法
2.1 算法理论基础
本问题的解可表达为
S=(s1,s2,…,snsolution),
(10)
s.t.si∈DT,
(11)
si≠sj,i≠j,
(12)
其中,S表示问题的一个解向量,即一种全局匹配方案,si表示S在向量维度i的值;DT表示S中元素的可取值集合.本文定义该类解的问题为离散排列向量解问题(discrete permutation vector solution problem, DPVSP),简称离散排列问题.当集合DT中的元素数量等于解向量S的维度nsolution时,称该问题为简单离散排列向量解问题(simple discrete permutation vector solution problem, SDPVSP),否则称为拓展的离散排解向量解问题(extend discrete permutation vector solution problem, EDPVSP),以下首先讨论SDPVSP的求解方法,然后再论述在EDPVSP下对该求解方法的拓展.
定义1.对SDPVSP的解Sα.通过交换解向量中第i和第j位置的值转化为一个新解Sβ,定义这种操作为单步交换操作(single step exchange oper-ation, SSEO),过程为
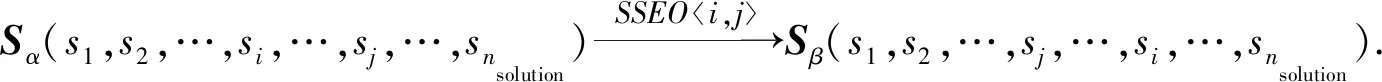
(13)
1) 对于DT元素数量大于向量维度nsolution的情况,将SSEO拓展为

(14)
其中DT-T表示DT与S各维度值的集合T的差集.拓展SSEO过程为,任意2个位置交换,或是某位置与DT中未被该解使用的离散值进行交换.经过拓展之后,仍满足上述性质.
2) 对于DT元素数量小于向量维度nsolution的情况,则对式(11)添加拓展元素null,则:

(15)
将约束式(12)变更为
si=sj,i≠j⟺si=sj=null,
(16)
对SSEO操作追加约束,则:
SSEOi,js.t.si≠null∨sj≠null.
(17)
式(16)表示null元素的可重用性,null元素可被重复使用;式(17)表明null元素的自身不可交换性,null元素不可与其他位置的null交换.
解空间图的解节点数量增多时,解空间图的结构会变得异常复杂,因而搜索高质量解也变得尤为困难.本文基于SDPVSP和单步交换操作解空间图(SSEOSSG),提出一种多策略解空间图搜索算法,简称解空间图搜索算法.该算法能够对解空间图进行快速且高效的搜索.
2.2 并行初始化价值矩阵与最短路径算法
设车主数量为m,乘客数量为n,以价值函数生成m×n的价值矩阵V,其中元素vij表示车主i和乘客j的价值.定义匹配方案矩阵X(m×n),矩阵中元素xij表示车主i与乘客j是否匹配且满足匹配互斥约束性.以下步骤均基于上述假设.
计算共享路程比率SRP过程中最大的计算开销为最短路径的计算.求解无负边的最短路径算法主要有Dijkstra算法和Floyd算法.对于本问题,Dijkstra算法的时间复杂度相较于Floyd算法更低.然而对于大型算例,Dijkstra算法计算开销仍然过大,因此本文对Dijkstra算法进行拆解并与价值矩阵的循环进行合并,可以在很大程度上降低时间开销.
原价值矩阵生成算法流程如算法1所示:
算法1.原价值矩阵生成算法.
输入:车主集合D,m=len(D)、乘客集合R,n=len(R);
输出:价值矩阵V.
① 初始化价值矩阵V[m][n];
② fordinD
③ forrinR
④Dis1=shortest_path(loc(r),dst(r));
/*r所在节点至目的节点的最短路径*/
⑤Dis2=shortest_path(loc(d),loc(r));
/*d所在节点至r所在节点的最短路径*/
⑥Dis3=shortest_path(dst(r),dst(d));
/*r目的节点至d目的节点的最短路径*/
⑦V[d][r]=SRP(Dis1,Dis2,Dis3);
/*根据Dis1,Dis2,Dis3求出d和r的SRP*/
⑧ end for
⑨ end for
Dijkstra算法可拆解为2个元操作:
1) 路径元操作.求所在节点至所有节点的最短路径.
2) 检索元操作.检索所在节点至目标节点的最短路径.
算法1的主要时间消耗在路径元操作.在对乘客进行遍历时,由于车主的所在节点和目标节点不变,因此可将路径元操作转移车主循环层级,即行②~⑨,这样可以减少n-1次路径元操作的计算次数,大幅降低时间开销.由于乘客循环和车主循环的顺序不影响结果,当车主数量少于乘客时,将车主作为外层循环也可降低路径元操作的计算次数.算法过程如算法2.
算法2.改进的价值矩阵生成算法.
总之,培养留守儿童良好的学习习惯需要家庭、学校、社会同关注、齐参与,我们教师作为留守儿童的“家庭外监护人”,在他们的家庭教育缺失的情况下,要通过不断地探索,让他们感受到教师的关爱,培养他们的自信心、自尊心,培养他们的自主学习的习惯,让他们在初中三年的学习和生活中温暖、充实、有收获。
输入:司机集合D,m=len(D)、乘客集合R,n=len(R);
输出:价值矩阵V.
① 初始化价值矩阵V[m][n];
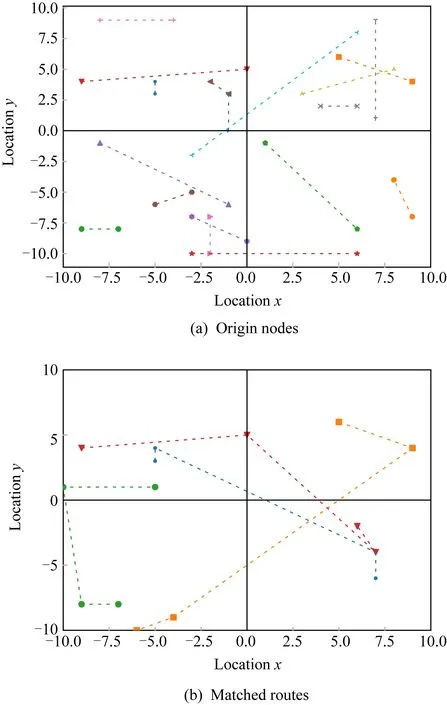
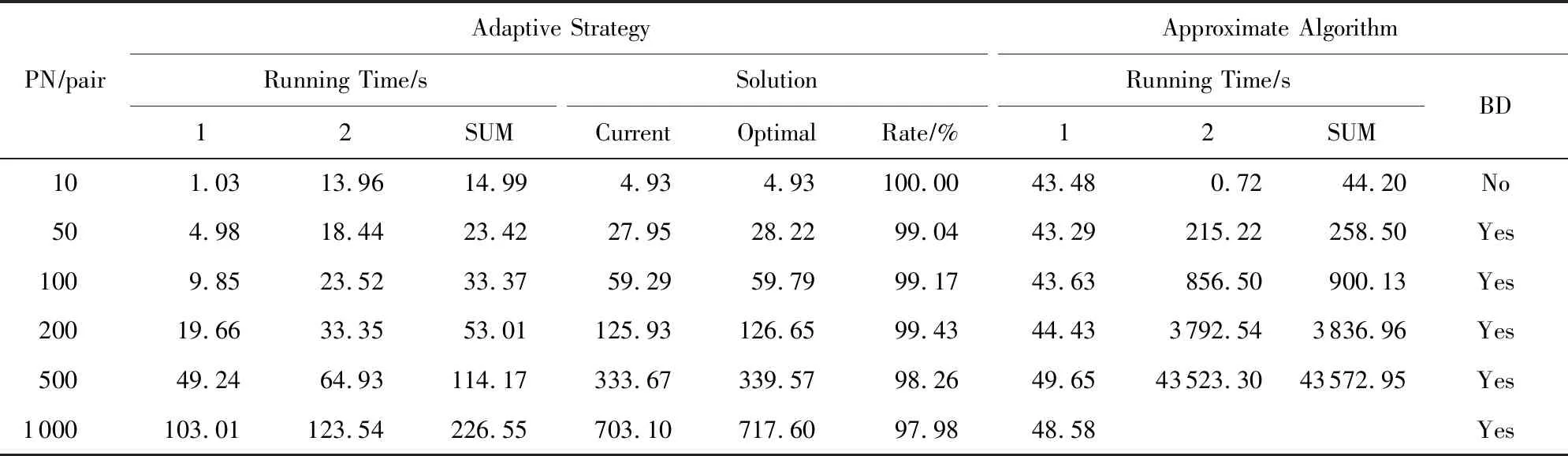
② ifm ③ fordinD ④Dis2Map=shortest_path(loc(d),all); /*d所在节点至所有节点的最短路径*/ ⑤Dis3Map=shortest_path(all,dst(d)); /*所有节点至d目标节点的最短路径*/ ⑥ forrinR /*r所在节点至目的节点的最短路径*/ ⑧Dis2=dis2Map[loc(d)][loc(r)]; /*从Dis2表中检索d所在节点至r所在节点的最短路径*/ ⑨Dis3=dis3Map[dst(r)][dst(d)]; ⑩V[d][r]=SRP(Dis1,Dis2,Dis3); /*根据Dis1,Dis2,Dis3求出d和r的SRP*/ /*所有节点至r所在节点的最短路径*/ /*r目标节点至所有节点的最短路径*/ 时间复杂度分析:在时间上,设道路图中的节点数量为nnode,边数量为nedge,乘客数量为n,车主数量为m,则对于原算法,单次Dijkstra算法使用邻接表和堆结构的时间复杂度为O(nedge×lbnnode),需要执行m×n次,故总体时间复杂度为O(m×n×nedge×lbnnode),通过缩减循环,实际总体执行Dijkstra算法的次数为min(m,n),故时间复杂度为O(nedge×lbnnode×min(m,n)).同时需要强调的是,以上处理并未增加空间开销. 算法在解空间图从1个初始节点开始迭代,初始节点的选择对算法的迭代速度有较大影响.为了保证算法对大算例的求解效率,初始解的生成方式必须是快速而高效的.本文设计一种大值优先算法来构造初始解,其过程如下: 对给定价值矩阵V,初始化解决方案数组X的所有元素置为0.对价值矩阵V的行进行遍历,对当前行所有数值进行排序,从最大值开始进行遍历,对于当前大值,判断匹配方案X中的该索引列的总和是否等于0,若是则将X中的该行该列置为1并跳过本行循环,否则对该行的下一个大值进行判断.重复上述过程,直到满足矩阵X的所有行之和都为1或者所有列之和都为1.算法过程如算法3所示. 算法3.大值优先算法. 输入:价值矩阵V; 输出:匹配方案X. ① 初始化X=zeros[m×n] /*X为m×n的矩阵,且初值为0*/ ② forrowinV ③ ifsum(X.rows)>0 orsum(X.cols)>0 break; ④ end if /*如果X的所有行都大于0或者所有列都大于0则结束*/ ⑤new_row=order_desc(row); /*对该行进行降序排序*/ ⑥ forlocationinnew_row/*对排序列进行遍历*/ ⑦ ifsum(X.col(location))=0 ⑧X[location]=1; ⑨ continue; /*如果当前值在价值矩阵中的位置,对应在匹配方案中的位置列之和为0,则将匹配方案中该位置置为1,并跳过此行*/ ⑩ end if 迭代算子是迭代优化算法的重要组成部分,对于离散排列向量解问题中,任何迭代算子的实质都是做1步或者多步SSEO操作. 本文使用解集覆盖性和收敛性对算子的特性进行分析.解集覆盖性越广,则算法对解集合的覆盖程度的期望越高,从而具有对解空间图更广的搜索范围,可在一定程度上避免解陷入局部最优.收敛性则指解向更优解移动的速度,具有该性质保证了算法在宏观上是收敛的,该性质越强,算法的收敛速度越快,但越容易陷入局部最优.解集覆盖性和收敛性是宏观互斥的. 1) 随机交换算子(random exchange operator, REO) 随机交换算子选取矩阵解X中的任意2行中匹配的位置的列进行交换.该交换算子的实质是使当前解在解空间图中向随机方向做1次SSEO,该算子的解集覆盖性非常强,但收敛性较弱. 数学公式描述为 选择 ∀xij,xkl: (18) s.t.xij=1,xkl=1, (19) (20) i≠k,j≠l. (21) 执行: xij=0,xkl=0,xil=1,xkj=1. (22) 时间复杂度分析:整个过程无循环,时间复杂度为O(1). 2) 上山交换算子(up-hill exchange operator, UEO) 该算子随机寻找矩阵解X某行,找到该行的匹配位置xij与某个价值比匹配位置大的xil,找到xil对应列l的匹配位置xkl,对xij和xkl所在行或列进行试探交换(行列的交换结果相同),如果2个位置交换后总体价值与交换前总体价值之差值非负,则提交交换操作.该算子的实质是向限制方向做1次SSEO.该算子的收敛性较强,解集覆盖性较弱. 数学公式描述为 选择 ∀xij,xkl: (23) s.t.xij=1,xkl=1, (24) (25) i≠k,j≠l, (26) vil≥vij. (27) 如果 vil+vkj≥vij+vkl (28) 执行: xij=0,xkl=0,xil=1,xkj=1. (29) 时间复杂度分析:过程中需对矩阵解X的行进行检索,时间复杂度为X行数O(n). 3) 概率上山交换算子(probability up-hill exchange operator, PUEO) 概率上山算子在随机找到第1行的匹配位置后,依据该行所有位置与当前匹配位置的差值,择取所有差值为正值的位置并依据差值做概率分布来随机选取下个位置,2个位置如果交换后价值增加,则进行交换.该算子的实质是向限制方向做1次SSEO.该算子的收敛性比上山交换算子更强,解集覆盖性则较弱. 数学公式描述为 选择 ∀xij,xkl: (30) s.t.xij=1,xkl=1, (31) (32) i≠k,j≠l, (33) vil≥vij, (34) (35) 如果 vil+vkj≥vij+vkl (36) 执行: xij=0,xkl=0,xil=1,xkj=1. (37) 其中pil表示位置il被选中的概率,当匹配位置价值vij等于最大值时,pij为所有等于最大值位置的数量的倒数,在其他情况下则为该位置与匹配位置价值插值与所有大于匹配位置的价值与匹配位置差值之和的比率. 时间复杂度分析:过程中需对矩阵解X的行进行检索,时间复杂度为X行数O(n). Fig.1 Random operator strategy flowchart图1 随机算子策略流程图 在迭代算子中已经提出,算子的解集覆盖性和收敛性是互斥的,因此本文定义一种结构来指导如何使用算子,通过调度多种算子来综合算法宏观的解集覆盖性和收敛性,使其2方面都达到较好的效果.本文把这种结构称为搜索策略. 搜索策略的终止条件在对比试验中可设为达到最优解一定比率停止,而在实际情况中可设置为固定迭代次数. 1) 随机算子策略(random operator strategy, ROS) 该策略随机使用3种算子,随机算子保证了算法的解集覆盖性,而另外2种算子则保证了算法的收敛性.流程图如图1所示. 2) 终点加速策略(end-charging strategy, ECS) 该策略随机使用随机算子和上山算子,在最后的数次迭代中,使用收敛性最强的的概率上山算子.随机使用随机算子和上山算子使得算法宏观的解集覆盖性较强,在终点前的加速又保证其收敛性.流程图如图2所示: Fig.2 End-charging strategy flowchart图2 终点加速策略流程图 3) 自适应策略(adaptive strategy, AS) 自适应策略基于当前解的迭代轨迹来指导解的搜索.策略监督解的收敛趋势,定义轨迹为每次迭代的解值的记录.由于迭代次数通常数量庞大而单次效果微小,因此只需每隔轨迹步长代数记录1次.自适应策略根据最近记忆长度次迭代值来分析当前收敛趋势,求记忆的轨迹中前几次值的均值与最近1次的值的差值,如果该差值高于高阈值,说明解正处于 收敛高势期,这时的解需要快速向最优解收敛,因此此时采用收敛性最强的概率上山算子,如果处于高低阈值之间,则说明解处于匀势上升期,使用上山算子即可,如果差值低于低阈值,说明解已经陷入局部最优,此时应该使用发散代数次随机算子发散解,使其随机移动到解空间的其他位置,跳出局部最优峰值后继续收敛.流程图如图3所示: Fig.3 Adaptive strategy flowchart图3 自适应策略流程图 本文使用模拟数据进行实验,采用的评估指标是算法运行时间和解的质量.模拟数据中,道路图数据通过OpenStreetMap Overpass API[注]http://www.overpass-api.de/获取,数据范围涵盖成都市2环内路网,并对道路节点进行了筛选和处理,节点与边的数量均为10 000,路网源数据的可视化如图4所示;车主乘客数据基于滴滴盖亚数据开放计划(didi chuxing gaia initiative[注]https://gaia.didichuxing.com),自成都市二环内局部区域轨迹数据中随机选取20/100/200/400/1000/2000/4000/6000名参与者,并随机指定50%为车主,50%为乘客,其中1 000和2 000数据规模的模拟分布图如图5所示.仿真语言为Python3.5,实验运行环境为2.50 GHz Intel Core i5-7300HQ CPU,8 GB RAM.最优解由KM算法[25]得出. Fig.4 Visualization of path network original data图4 路网源数据可视化 Fig.5 Distribution of drivers and riders图5 车主乘客分布 并行的价值矩阵生成算法与普通的价值矩阵生成算法的时间比较见图6和表2.表2记录了乘客车主对数量、普通价值矩阵生成算法和并行的价值矩阵生成算法的运行时间. Fig.6 Graph of running time between concurrence value matrix generation and normal generation图6 并行价值矩阵生成与普通生成的运行时间图 Table 2 Table of Running Time Between Parallel Value Matrix Generation and Normal Generation ParticipantNumber∕pairRunning Time∕sParallel GenerationNormal Generation100.946.67504.67144.121009.42563.1220018.492267.7850047.5613712.901000108.36 通过实验结果可以看出,该算法大幅度节省了时间.在处理500对乘客车主的算例时,改进算法的运行时间仅为普通算法的0.35%. 图7和表3展示了对随机算子策略的评估结果.表3记录了乘客车主对数量、5组达到最优解95%的较优解的时间、占最优解价值的比率及其均值、最优算法时间. Fig.7 Random operator strategy contrast graph图7 随机算子策略对照图 分析所得数据,可以发现随机算子策略获取近似解速度较快,且随着数据规模的增大,该策略与最优算法的时间消耗差异明显.实验结果表明:随机算子策略可以显著提升给出较优方案的时间.在求解规模为500对的算例时,随机算子策略的运行时间为最优算法的61.85%,当算例增大到3 000对时,随机算子策略所需时间仅为最优算法的25.04%. Table 3 Random Operator Strategy Data Size Table表3 随机算子策略数据规模表 Notes: PN represents participant number; OART represents optimal algorithm running time. 3.3.1 终点加速策略中终点距离的影响 本节测试终点距离对算法的影响,对终点距离的实验都是在1 000对乘客与车主的数据规模之下的,实验结果如表4所示.表4记录了终点距离代数、5组达到最优解95%的较优解的时间、占最优解价值的比率及其均值. 实验结果表明这个参数并不会显著地影响该策略的速度,运行时间存在的少许差异可能是运行过程的随机性或者是误差造成的. Table 4 Charge Length for End-Charging Strategy Table 表4 终点加速策略终点长度表 Notes: CL represents charging length. 3.3.2 终点加速策略在不同实验规模下的效果 经过终点长度的实验后,选择长度50作为接下来在不同数据规模下该策略的运行时间的实验,结果如表5所示,对照图如图8所示.表5记录了乘客车主对数量、5组达到最优解95%的较优解的时间、占最优解价值的比率及其均值、最优算法时间. Table 5 End-charging Strategy in Different Data Size Table表5 终点加速策略数据规模表 Notes: PN represents participant number; OART represents optimal algorithm running time. Fig.8 End-Charging strategy contrast graph图8 终点加速策略对照图 终点加速策略也比最优算法运行时间短,但在小算例速度比随机算子策略慢,分析这个过程,终点加速策略中收敛性最强的概率上山算子的运行次数相对较少,这说明概率上山算子对小算例的收敛速度提升的效果较为显著,大算例时概率上山算子对速度的影响变差.当算例超过3 000对时,终点加速策略的运行时间优于随机算子策略. 3.4.1 自适应策略中发散代数的影响 本节研究发散代数对该策略的影响,实验参数为:步长为100,记忆长度为2,高阈值为10-4,低阈值为10-10,乘客车主对数量为1 000对.实验结果如表6所示.表6记录了发散代数、5组达到最优解95%的较优解的时间、占最优解价值的比率及其均值. 从实验结果中可以发现,这个参数对运行速度有影响.以50代的平均运行时间为标准,其他代数运行时间约为50代平均运行时间的80%~140%(不考虑缺省值).从实验结果还可以看出,当发散代数超过90代时开始出现发散现象,此时算法过程不再收敛. 3.4.2 自适应策略中记忆长度的影响 本节研究记忆长度对自适应策略的影响,本节其他参数为步长100,发散代数为20,高阈值为10-4,低阈值为10-10,发散代数为20,乘客车主对数量为1 000对.实验结果如表7所示. 表7记录了记忆长度、5组达到最优解95%的较优解的时间、占最优解价值的比率及其均值. Table 6 Divergence Length for Adaptive Strategy Table表6 自适应策略发散代数表 Notes: DL represents divergence length. Table 7 Memory Length for Adaptive Strategy Table表7 自适应策略记忆长度表 Notes: ML represents memory length. 实验结果表明记忆长度变大会增涨算法的运行时间,记忆长度为9时的平均运行时间是长度为2时的143.35%. 3.4.3 自适应策略中阈值的影响 本节研究高低阈值对结果的影响,由于高低阈值之间存在约束,所以将其放在一起实验.本节其他参数为步长100,记忆长度为2,发散代数20,乘客车主对数量为1 000对.实验结果如表8所示. 表8记录了记忆长度、5组达到最优解95%的较优解的时间、占最优解价值的比率及其均值. Table 8 Threshold for Adaptive Strategy Table表8 自适应策略阈值表 Notes: HT represents negative base-10 logarithm of high threshold; LT represents negative base-10 logarithm of low threshold. 实验结果表明:高低阈值能在一定程度内降低过程的消耗时间.以高阈值为10-2,低阈值为10-8为标况下,高阈值变化会使结果在81.95%~100%范围浮动,而低阈值则处于79.01%~100%.它们的效果都不是特别显著. 3.4.4 自适应策略在不同实验规模下的效果 本节考察自适应策略在不同算例下的运行结果.实验参数为:步长为100,高阈值为10-4,低阈值为10-10,发散代数为20,记忆长度为2.实验结果见图9和表9.表9记录了乘客车主对数量、5组达到最优解95%的较优解的时间、占最优解价值的比率及其均值、最优算法时间. 分析实验结果,自适应策略在1 000对以下,虽然劣于随机算子策略,但此时运行时间较短,差距不超过3 s.自适应策略在1 000对算例以上运行时间开始显著优于随机算子策略和终点加速策略.在1 000对算例时,自适应策略的平均运行时间为随机算子策略的77.67%,标准算法的38.44%.在3 000对算例时,自适应策略的平均运行时间为随机算子策略的72.76%,终点加速策略的78.41%,标准算法的18.22%. Fig.9 Adaptive strategy contrast graph图9 自适应策略对照图 Table 9 Adaptive Strategy in Different Data Size Table表9 自适应策略数据规模表 Notes: PN represents participant number; OART represents optimal algorithm running time. Fig.10 Convergence trend of multiple strategy in iterations times图10 各策略的迭代次数收敛趋势 3种模式的收敛趋势如图10和图11所示.表10展示了在不同的乘客司机对的数量之下不使用共享匹配的总行驶路程、使用共享匹配后的总行驶路程、共享匹配后总节约路程.图12则展示了部分乘客与车主的匹配结果. Fig.11 Convergence trend of multiple strategy in running time图11 各策略的运行时间收敛趋势 Table 10 Route Contrast Table ParticipantNumber∕pairTotal DistanceUnshared WayShared WaySavedDistance5069806435545100140341163923952002771921749597050066332487291760310001322689188240386 Fig.12 Matching result of partial drivers and riders图12 部分车主乘客匹配效果图 本节对本文算法和一种较新的近似值方法[11]进行实验以比较求解效率和质量. 本节选取的策略为自适应策略,参数为:步长为100,发散代数为50,高阈值为10-3,低阈值为10-6,记忆长度为2,迭代次数为10万次.近似值方法的参数为:分区为10区,拟合率为1.05(保证该算法的求解质量达到最优解的95.24%以上). 需要指出的是,本文的问题模型与文献[11]中的模型不同,因此删去了其模型中车主的要求SRP值.此外,该近似方法可能发生退化,在发生退化时,其可获得真实乘客车主二分图的价值矩阵,并使用最优解算法来寻找最优解. 实验结果如表11所示.表11记录了乘客车主数量、自适应策略2个阶段及总体的运行时间、自适应策略的解的SRP值、最优解SRP值、自适应策略的解占最优解的比率、近似值方法2个阶段及总体的运行时间(不包括退化后使用最优算法的时间)、近似值方法是否退化. Table 11 Comparison Between Adaptive Strategy and Approximate Algorithm for Join-based RS表11 自适应策略与基于连接的车辆共乘近似值方法比较表 Notes: PN represents participant number; Rate represents the ratio of current solution to optimal solution in percentage; BD represents whether approximate algorithm has degenerated. 从实验结果中可以看出,本文方法的速度相较于近似值算法有较大提升,在10对算例下,自适应策略运行时间为近似值算法的33.91%,算例达到500对时,自适应策略运行时间仅为近似值算法的0.26%. 本文提出了一种基于单步交换操作解空间图的解搜索算法.首先,提出了一种兼顾资源利用率和方案可行性的价值评估方法;然后对价值矩阵的生成方式作出了改进;接着提出了3种搜索算子,并根据3种搜索算子设计了3种搜索策略;最后通过实验测试了各策略对其相应参数的敏感性,并与标准算法及一种较新的近似值方法作了比较.实验研究表明,本文算法的各个策略都能给出接近最优解SRP 95%以上的高质量解,并且在大部分的算例中运行时间比标准算法和近似值方法有显著的降低. 在下一阶段的研究中,我们将考虑动态时间窗模式下的车辆共乘问题.动态时间窗模式下,车主和乘客的请求将被动态地加载,此时需考虑窗体的划分方法与全局价值的最大化.车辆共乘问题各种模型始终存在一定差异性,下一阶段研究将致力于针对动态车辆共乘问题提出一种可泛化的有效的模型和解决方法.2.3 大值优先算法生成初始解
2.4 迭代算子



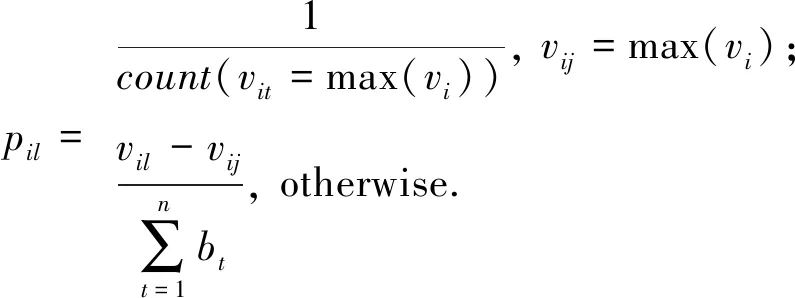
2.5 搜索策略
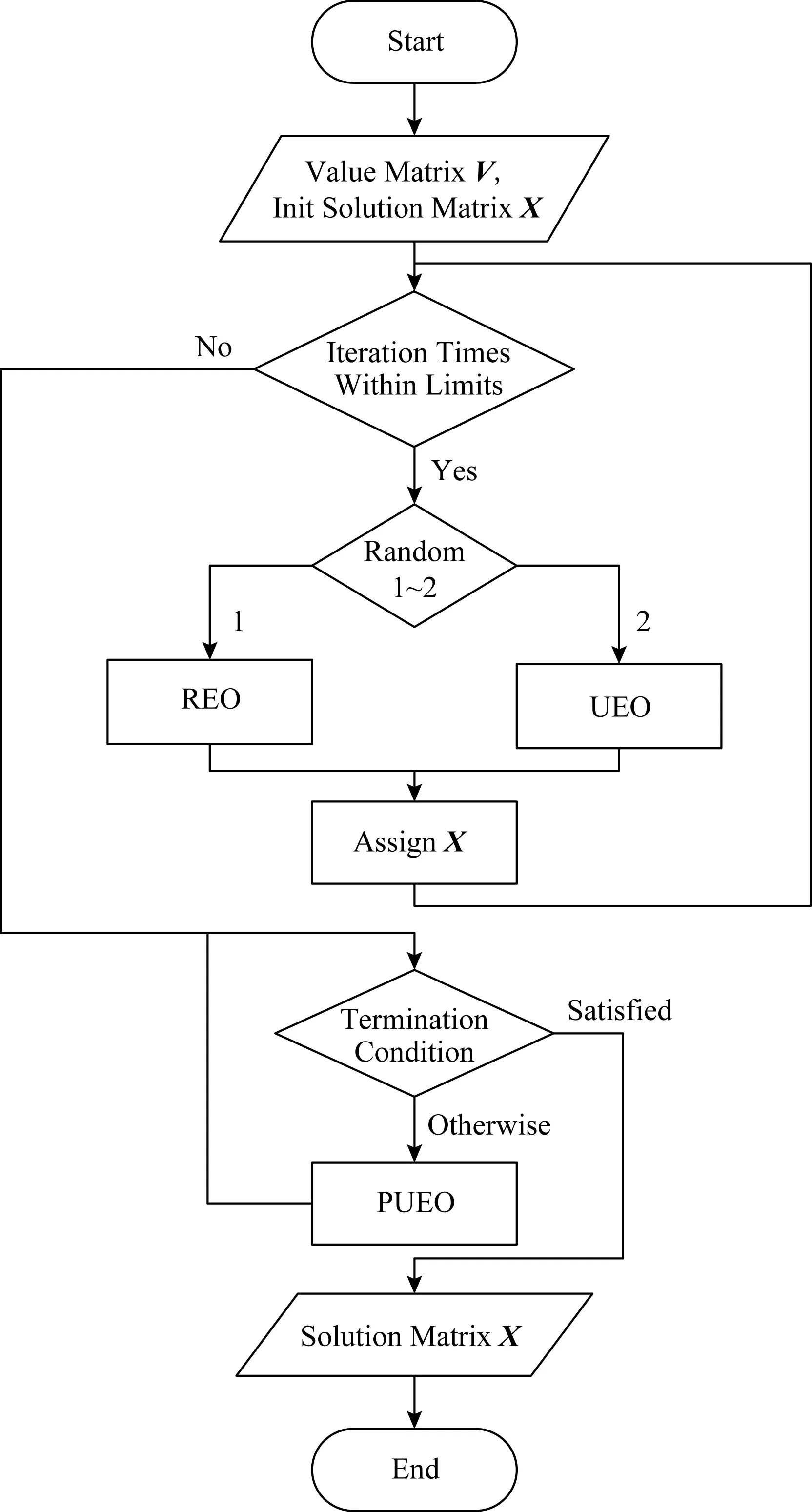
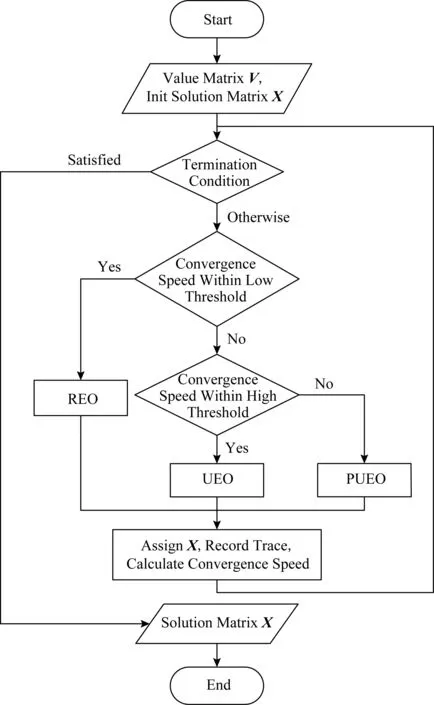
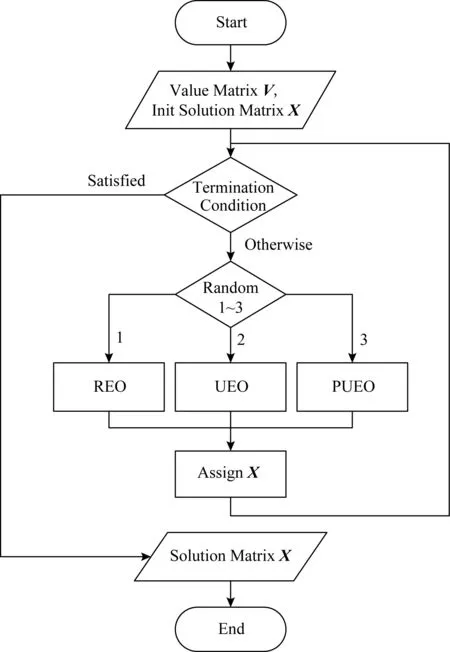
3 实验与分析
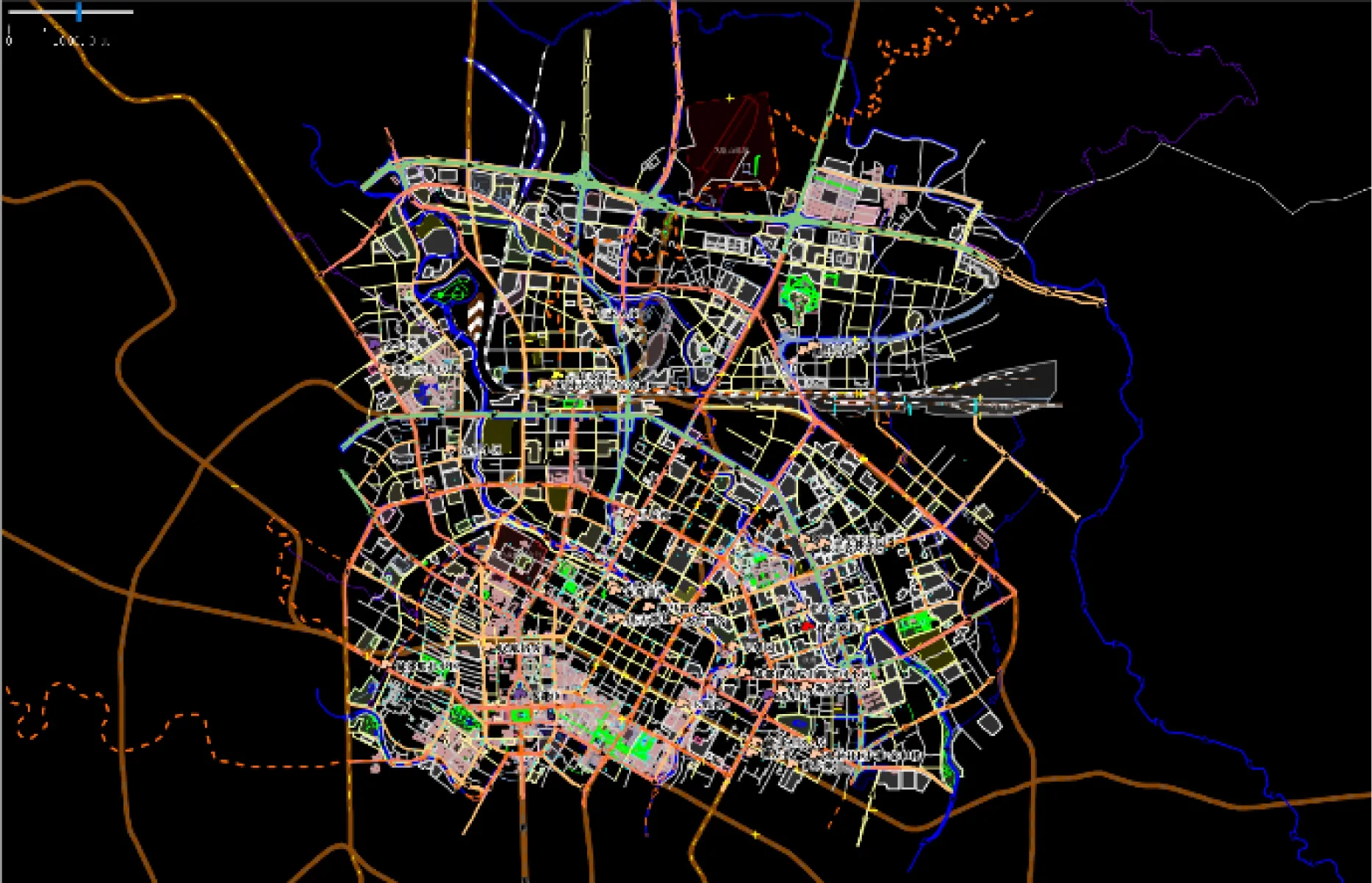
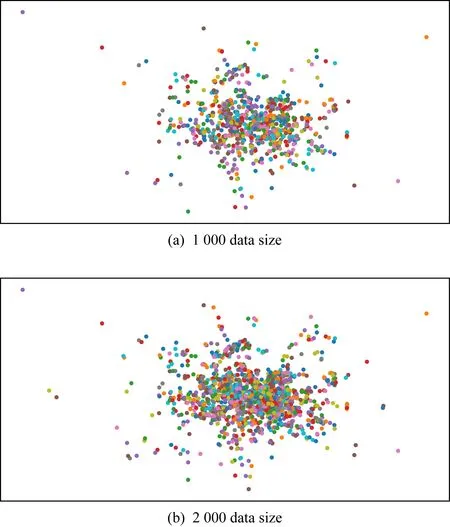
3.1 价值矩阵生成时间对比
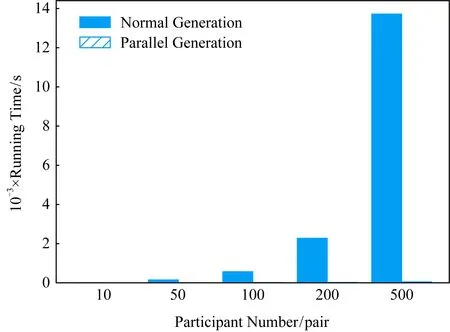
表2 并行价值矩阵生成与普通生成的运行时间表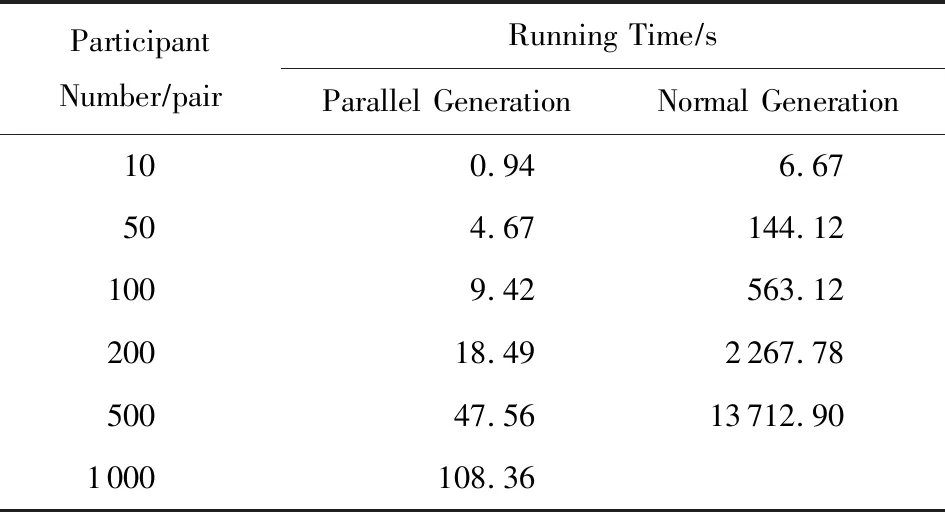
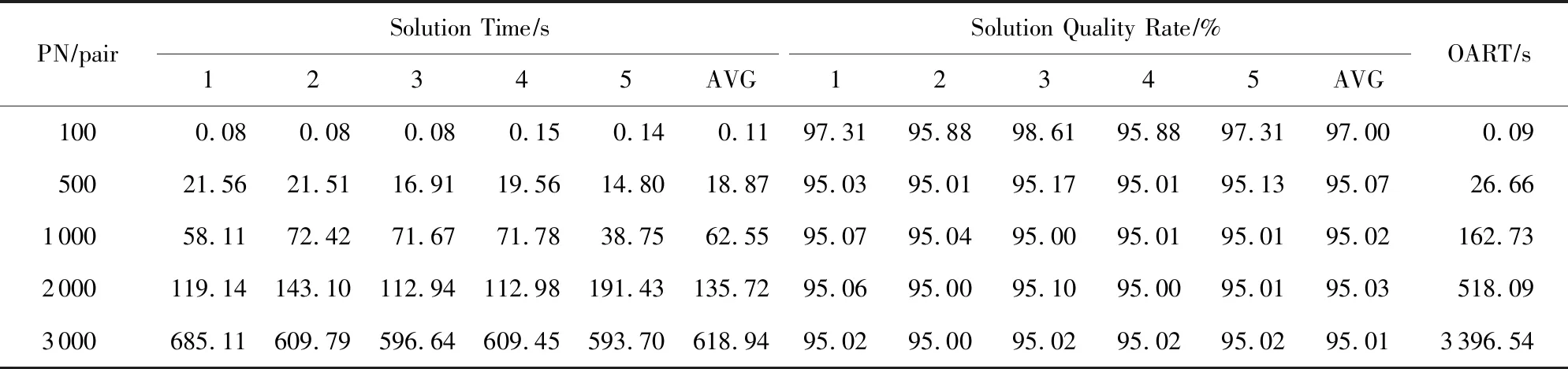
3.2 随机算子策略
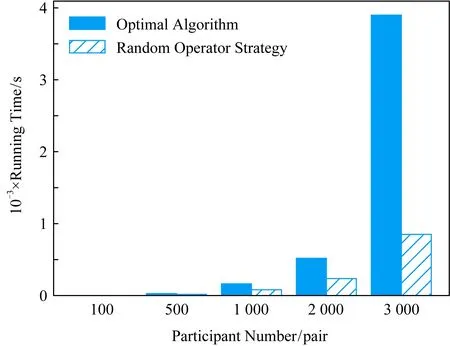
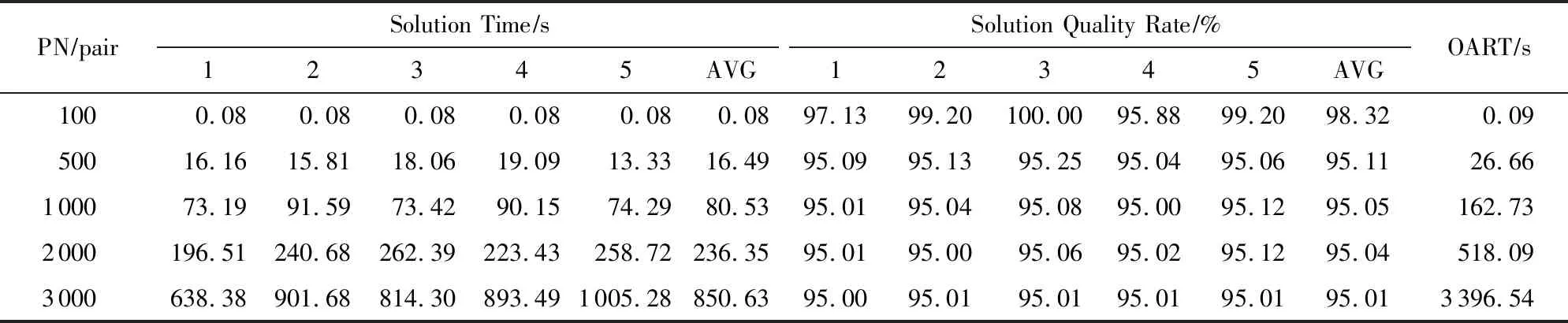
3.3 终点加速策略
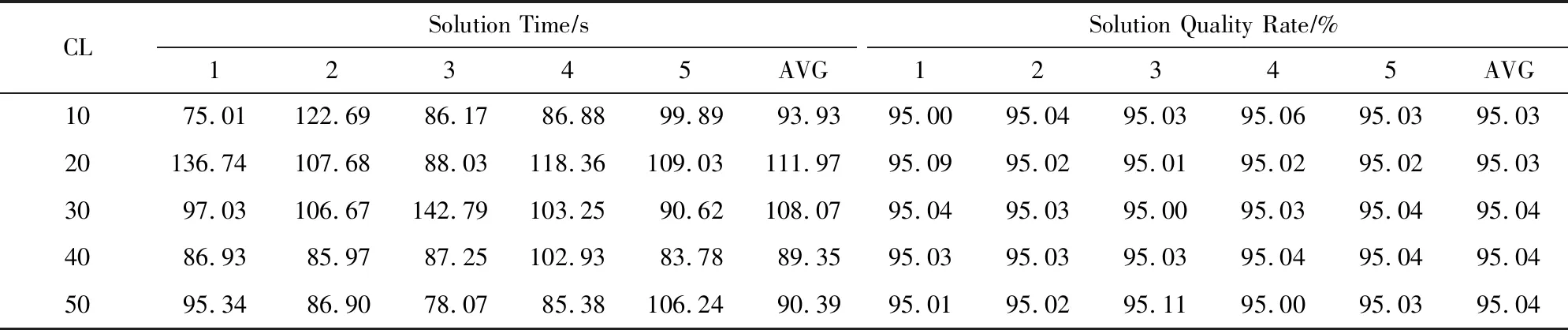
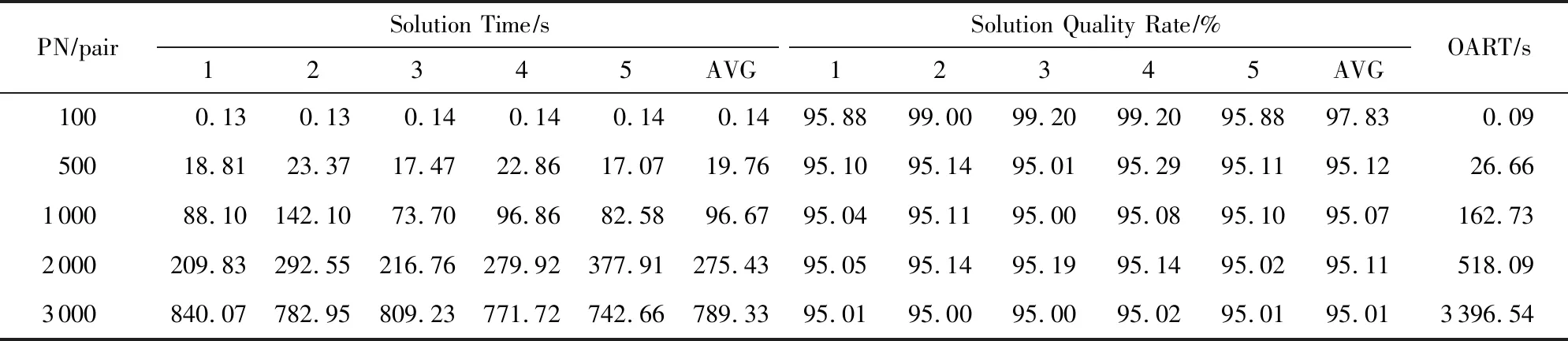
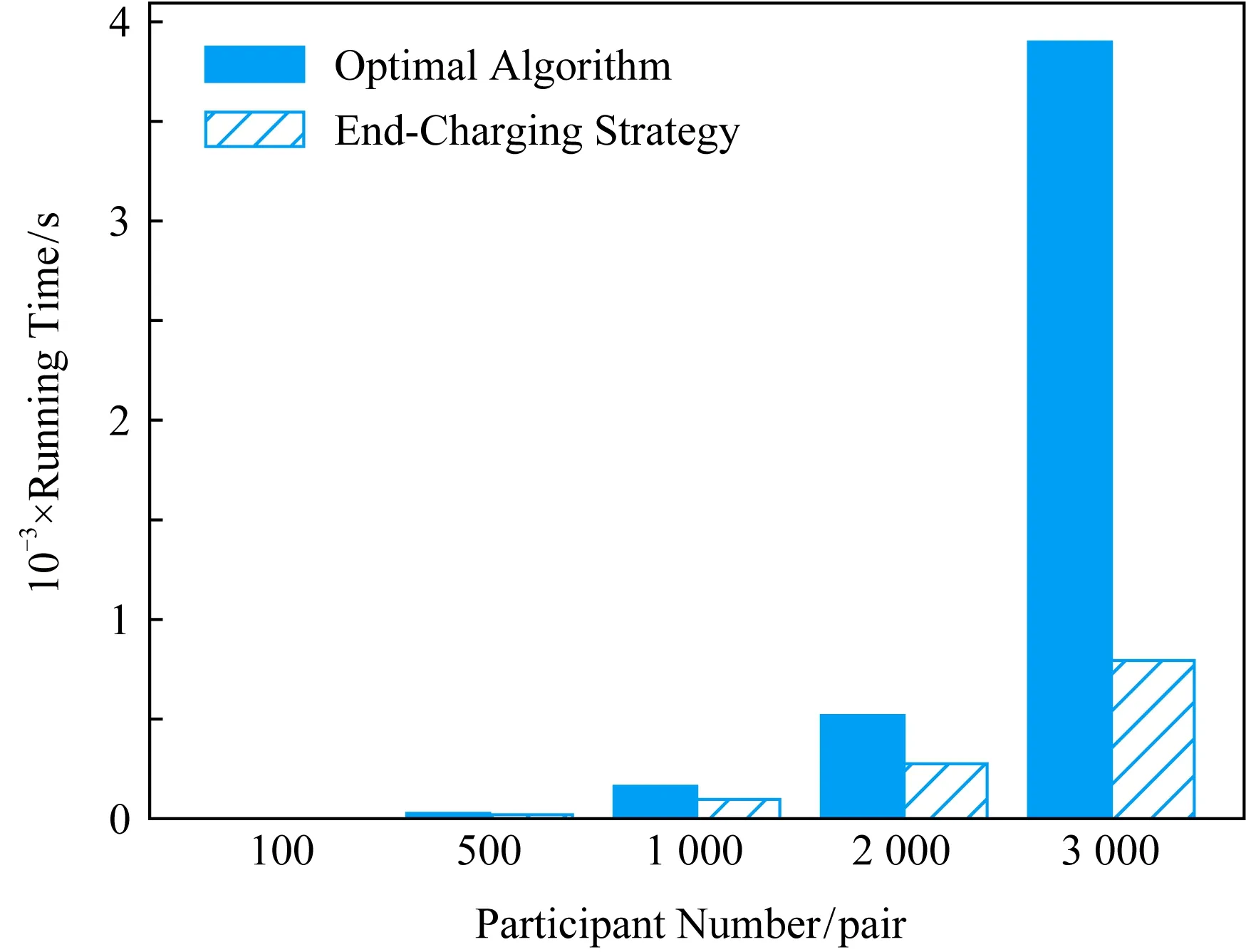
3.4 自适应策略
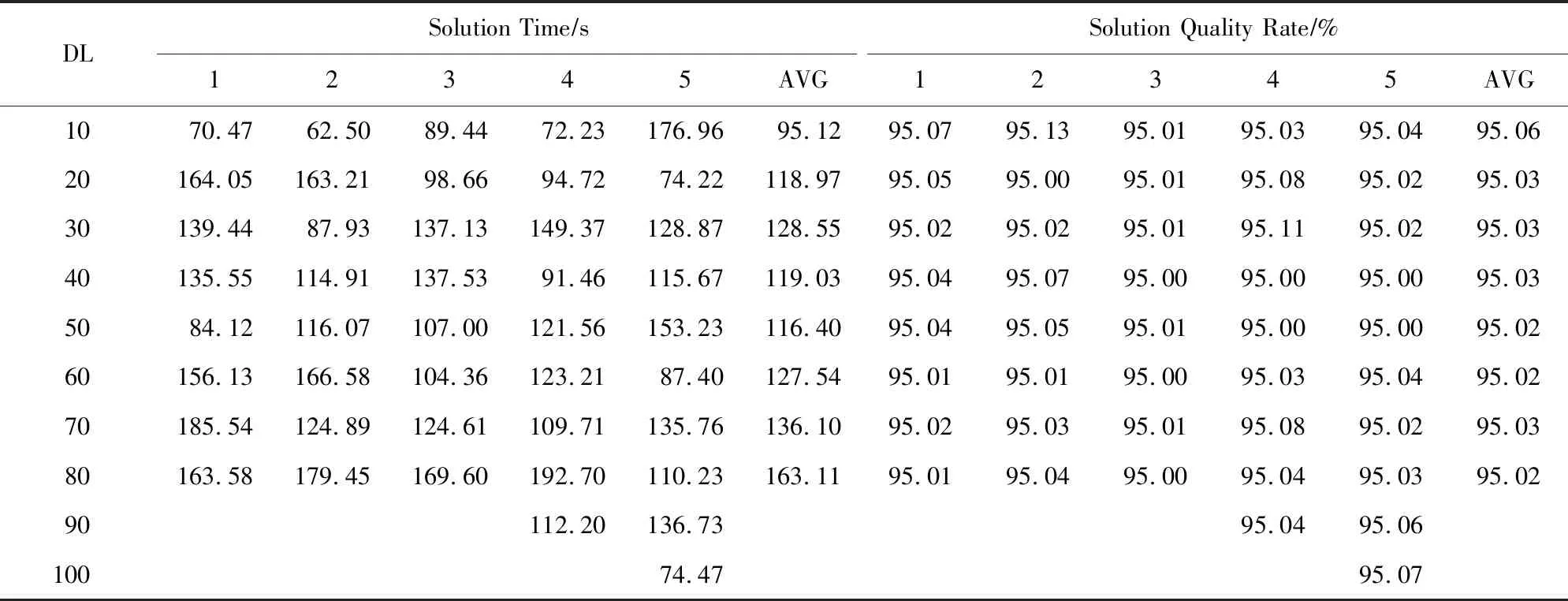
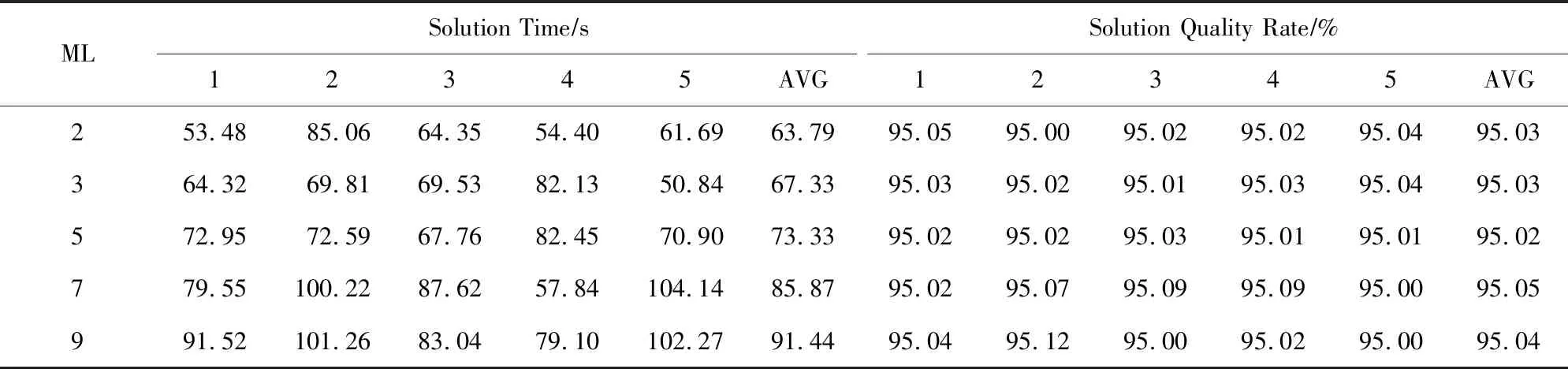
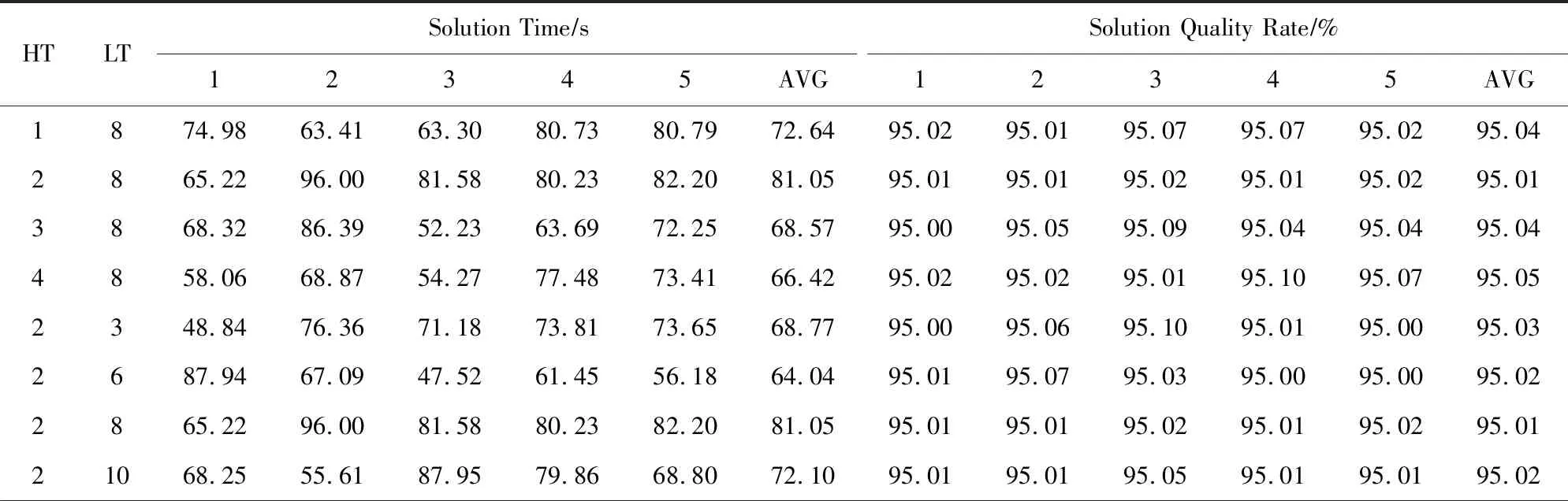
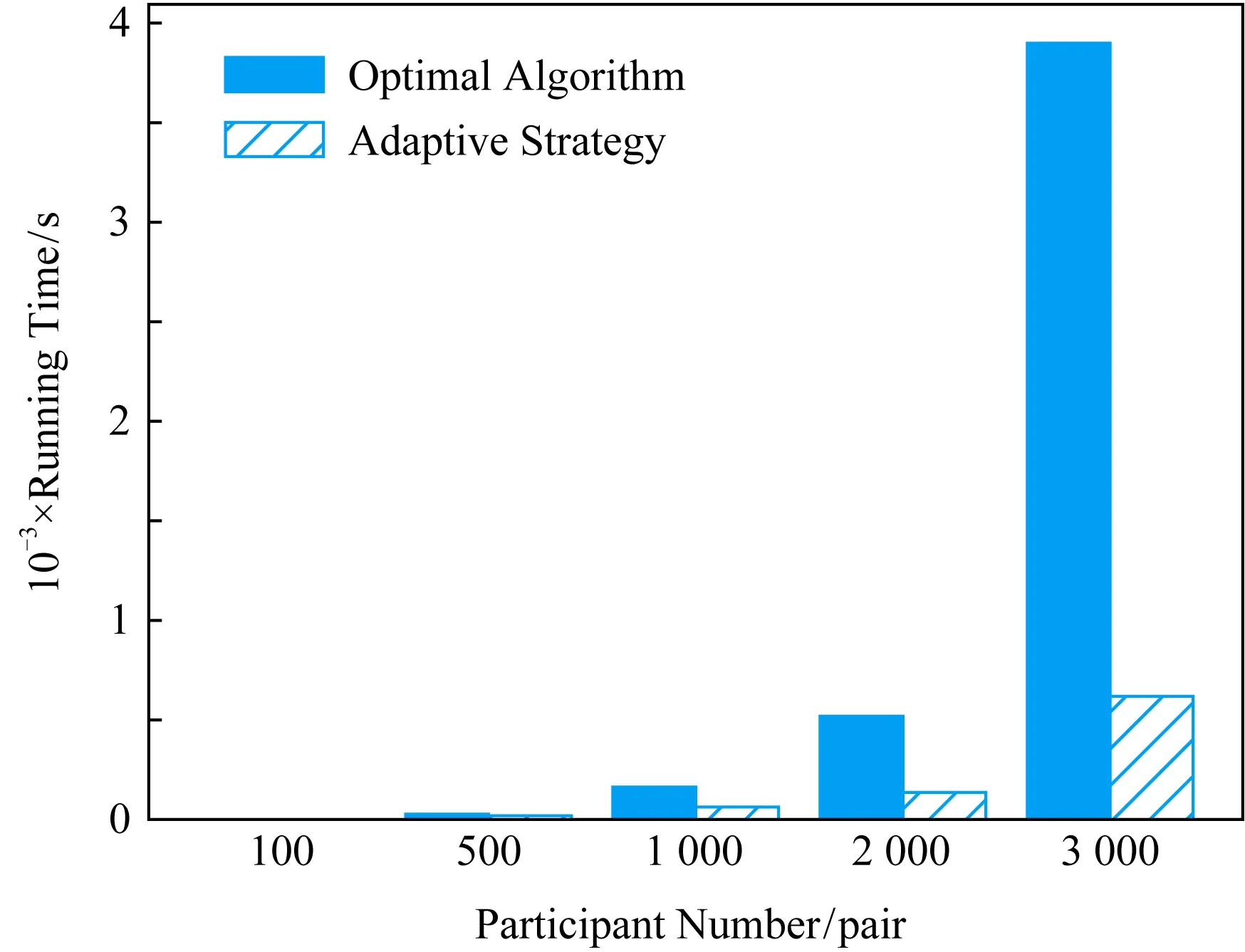

3.5 模式收敛趋势及共享匹配结果
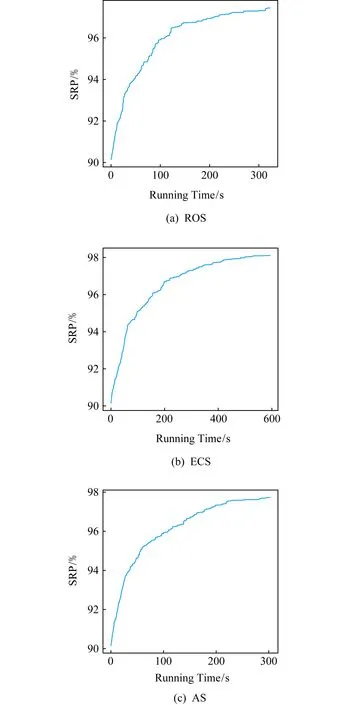
表10 路程对比表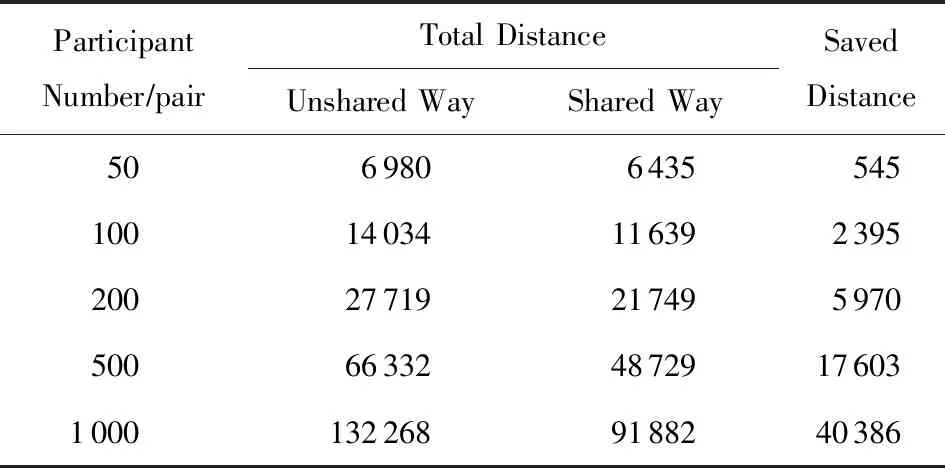
3.6 本文算法和一种基于连接的近似值方法的比较
4 总结与展望

