蜂窝夹层复合材料小质量冲击接触力的分析

李 娜， 尤青文,2

(1.上海飞机设计研究院，上海 201210； 2.上海交通大学航空航天学院，上海 200240)

蜂窝夹层复合材料由上下复合材料面板和中间的蜂窝夹层构成，由于其质量较轻，具有高强度比、高刚度比的特点，同时蜂窝芯材对面板有较好的支撑，使其不易失稳，因此蜂窝夹层复合材料被广泛应用在航空等领域。夹层结构传递载荷的方式和工字梁比较相似，芯材承担由横向力产生的剪应力，而面板主要承担由弯矩引起的面内拉压应力和面内剪应力。上、下面板间的距离使截面惯性矩增大，提高了结构的弯曲刚度以及材料的利用率。

由于有蜂窝芯材的存在，蜂窝夹层板损伤形式包括基体的损伤、面板分层、芯材压溃、纤维断裂、穿透等多种不同的形式[1]。当蜂窝夹层复合材料受到小质量高速物体的冲击之后，面板及蜂窝内部容易产生不易观察的损伤，对于结构强度会有重要影响[2]。更有甚者，当面板出现裂纹之后，水流会沿着裂纹进入到蜂窝夹层复合材料内部，当飞机升空后会结冰，体积变大，损坏内部的结构。

目前在蜂窝夹层复合材料的小质量冲击实验方面，多采用气枪发射小铁球的方式产生冲击。Aktay等[3]利用气枪进行蜂窝夹层复合材料的冲击，然后用有限元的方法进行仿真，可以发现两者结果吻合较好；Hazell等[4]用小钢球对复合材料层压板进行正冲击和斜冲击，并且速度达到可穿透层压板的程度，结果发现不同的冲击速度下，层压板穿透的形式不同，有的是背部的拉伸损伤为主，有的是钢球穿透为主；Stronge[5]探究了斜冲击情况下表面摩擦的影响，如果冲头最初接触层压板表面时有初始的滑动，则这个滑动会伴随着冲击的整个过程，会对层压板的能量吸收产生较大影响；卞栋梁等[6]通过对某型飞机上应用的Nomex蜂窝夹芯板进行冲击实验，研究厚度对其抗冲击损伤能力及冲击后轴压承载性能的影响，结果表明，蜂窝夹芯厚度的增加可以有效提高结构整体的抗冲击性能及能量的吸收；Passieux等[7]使用气枪发射小铁球，撞击覆盖着蜂窝夹层复合材料的机翼模型，同时通过高速摄像机对冲击前后的图像进行拍摄，当改变气枪发射角度时，可以模拟不同角度下的斜冲击情形。同时，通过高速摄像机记录冲击过程中小铁球的运动状态，通过其加速度得到冲击接触力；Messaadi等[8]也利用小铁球冲击层压板，当变换层压板的角度时，可以模拟不同冲击角度的斜冲击情形，通过比较试验和有限元仿真结果之间的关系，发现了冲击角度和物体表面摩擦系数对板表面的破坏机理有很大影响；Zhou等[9]对层合板和夹层板进行不同角度的冲击，并分析损伤结果，最终认为在0°～45°冲击角度冲击下，蜂窝夹层复合材料能够承受较大速度的冲击，但是仅仅对冲击之后的损伤结果进行分析检测，对冲击力等数据并未采集和分析。

Pernas-Sánchez等[10]对复合材料层压板进行了高速冲击，然后分别进行无损和有损检测，同时提出了能量吸收的解析模型，可以发现斜冲击下的损伤面积比正冲击下要小，并且能量吸收主要是由分层和纤维断裂造成；Xie等[11]通过小钢球分别正冲击和斜冲击复合材料层压板，发现不同的冲击形式有着不同的能量吸收准则，因此提出了能量极限值的概念，在极限值以下，正冲击的损伤区域更大，而在极限值以上，情况则是相反的；Gupta等[12]对夹层结构分别进行了高速冲击，发现斜冲击的剩余速度大于正冲击的剩余速度，也就是正冲击时候夹层结构吸收的能量会更多。

可见，目前对于蜂窝夹层材料小质量物体冲击的测试主要采用气枪发射钢珠、子弹等方法，但是这些方法不能够直接测量接触力，因此将测量接触力与理论结果对比的研究也较少。叶文勋等[13]通过研发小质量冲击试验机，发展了复合材料层压板小质量物体冲击测试技术，实现了冲头速度和冲击点挠度的测量。在此基础上，笔者首先对小质量冲击试验机进行改进，使其能够进行斜冲击测试，然后开展多角度的小质量冲击实验，最后通过在以前的理论模型上增加刚度折减模型，模拟出冲击接触力。

1 层压板小质量冲击的工程模拟方法

1.1 局部接触变形模拟

Olsson[14]用冲头和层压板的质量比作为冲击类型划分的依据，对矩形板而言，当冲击体与板的质量比小于0.23的时候，冲击类型为小质量冲击，该类冲击下板的响应中包含高阶的模态。蜂窝夹层板小质量冲击下[15]，当冲头以某一速度冲击到蜂窝夹层板表面时，层压板发生变形，接触力会逐渐增大。其中夹层板的变形值α可以分为两部分，分别是面板的压缩值αH，以及由于面板凹陷发生的变形αF，其中αH通常较小，根据赫兹接触理论，存在以下的关系式：

(1)

(2)

式中：αF为凹陷值，m；F为冲击接触力，N；kH为面板的接触刚度，N/m3/2；QH为等效面外刚度，N/m2；R为冲头半径，m。

对于凹陷值αF，在不同的阶段存在不同的特点，因此求解方法也存在差异。当接触力逐渐增大到蜂窝芯材的压溃力Fcr的时候，局部变形可以用小变形理论求解，其中变形值αF可以表示为

(3)

式(3)中：

(4)

(5)

(6)

(7)

(8)

当冲击接触力大于Fcr，即芯材损坏之后，整体面板分为两部分，分别为芯材损伤区域，该区域均布载荷支撑，以及芯材损伤区域之外的区域，此处仍然为弹性区域，如图1所示[16]。

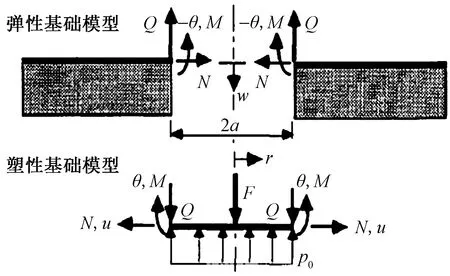
图1 非弹性阶段的受力图Fig.1 The stress in the inelastic range

此时面板变形可以用小变形板理论或者膜理论计算。首先引入无量纲量如下：

(9)

(10)

(11)

式中：pcr为芯材压溃的临界应力，N/m；αi为芯材损伤区域的半径，m；M为芯材损伤区域边界的分布弯矩，N；此时变形值：

(12)

αcr=αF(Fcr)

(13)

当接触力继续增大到Fdth时，面板发生分层。面板分层之后会大大降低弯曲刚度，但是分层不会降低膜的刚度。因此，面板分层之后的接触力响应可以根据膜理论求解，得到的变形值：

(14)

式(14)中：am为是芯材压溃区域半径，m；s1为接触半径和芯材压溃半径的比值;Ff为发生纤维断裂损伤时的接触力，N；wm为当层压板受到集中载荷F时的变形，m。

(15)

1.2 小质量冲击响应模型

考虑了板的等效刚度D*和等效剪切刚度S*之后，剪切变形引起的蜂窝夹层复合材料的位移可以表达成下列积分式[17]：

(16)

(17)

(18)

(19)

(20)

(21)

式中：m为面密度，kg/m2；T为只考虑接触刚度情况下的冲击周期，s，如果初始冲击速度为V0，则T的定义为

(22)

式(22)中：kα为冲头与蜂窝夹层板的接触刚度，N/m3/2，初始条件为

(23)

经过无量纲化后，蜂窝夹层板受到小质量外来物体冲击的运动方程为

(24)

接触刚度kα与接触力和压入的总位移有关，用下式计算：

(25)

如果处于弹性接触状态，kα计算方法为

(26)

当蜂窝夹层复合材料芯材损伤而面板未损伤时，有：

(27)

当最终面板分层以后，面板刚度会剧烈减小，假定面板最大的分层数为nmax，则分层区域的等效弯曲刚度：

(28)

最后，蜂窝夹层板受到小质量外来物体冲击时的接触力为

F=kαα

(29)

2 实验方法

实验用到的小质量多角度冲击设备如图2所示，此设备是在已有小质量冲击试验机[18]的基础上改进而成，改进之后的实验设备可以模拟小质量物体对材料的多方向冲击。

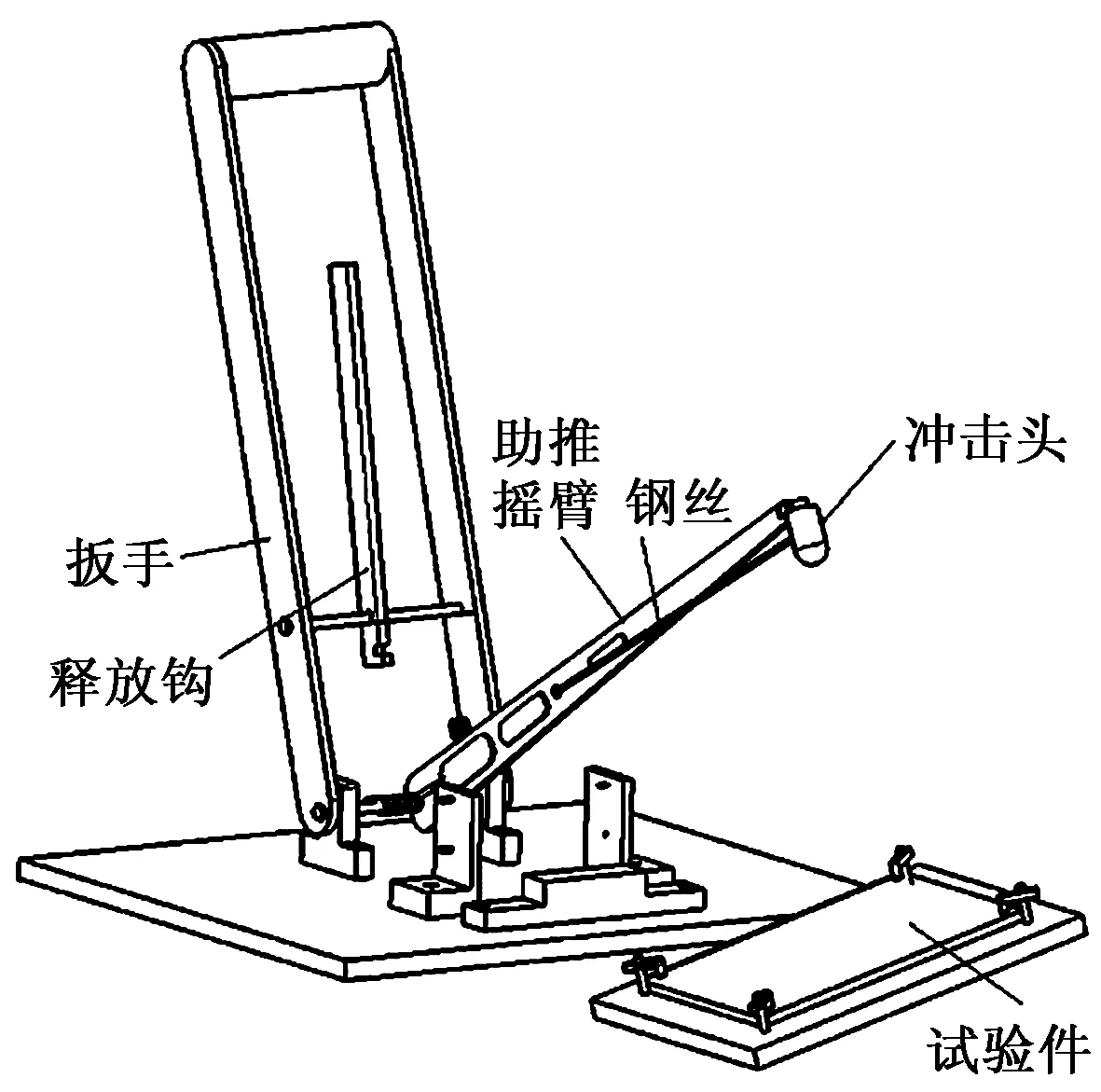
图2 小质量冲击设备简图Fig.2 Configuration of small-mass impact instrument

该设备的冲击头通过细钢丝连接到摇臂上，摇臂端部有卡槽，可推动钢丝和冲击头一起运动。通过扳手带动释放钩，将摇臂、钢丝和冲头拉起。当达到预定角度时，松开释放钩，在扭簧的作用力下，摇臂前端的卡槽推动钢丝和冲击头加速，当摇臂经过光电传感器时，光电传感器会记录到信号，从而可以得到摇臂的冲击速度和冲击能量。当摇臂撞击到撞击支座时，摇臂停止运动，钢丝会脱离卡槽，跟随冲击头继续运动，使冲击头撞击到试验件不会飞出。由于钢丝较细，冲击头在冲击过程中可以近似为无约束运动，可以较好模拟自由物体的冲击。加速度传感器安装在冲头尾部，通过冲击头的加速度计的信号，可以求得冲击接触力。

实验采用的冲头前部为半圆形，后部为圆柱形，质量为30 g，实验时采样频率为1 MHz。

3 实验与仿真结果的对比

当用1.51 J的能量垂直冲击两种试验件时，经过滤波后，最终得到的滤波之后的冲击接触力和理论模拟之后的冲击力对比如图3和图4所示。实验之后，面板出现凹坑，蜂窝夹芯复合材料变为非弹性状态，即发生了芯材的压溃和面板的分层。

表1 单向带的参数Table 1 Parameters of unidirectional tape

表2 蜂窝的参数Table 2 The parameters of honeycomb

图3 实验和仿真的接触力(hf=0.5 mm；E=1.51 J)Fig.3 The experimental force and simulated force (hf=0.5 mm，E=1.51 J)

图4 实验和仿真的接触力(hf=0.8 mm，E=1.51 J)Fig.4 The experimental force and simulated force (hf=0.8 mm，E=1.51 J)

通过对比图3和图4中的接触力可以发现，对于芯材相同的夹层复合材料，相同的冲击能量下，面板层数越多，冲击接触力越大，这是由于面板层数增加的时候，面板的接触刚度会迅速增加，也可见面板刚度对接触力影响明显。

另外也会发现，由于通过加速度计来测量冲击过程的接触力，加速度计可能在冲击过程中会产生抖动，从而干扰测量信号。并且，在夹层板产生损伤，如面板分层、纤维断裂时，所测接触力曲线会有较多的抖动，但是整体的趋势和数值等能够反应真实情况。

当对试验件进行斜冲击时，为了仿真冲击载荷，对冲击力和冲击速度进行法向和切向的分解，如图5和图6所示。实验中加速度计测得的冲击接触力为F，对接触力进行分解，得到在垂直于夹层结构面板方向的接触力为F1。同理，当实验测得的冲击速度为v时，分解得到的垂直于面板方向的速度为v1，最后将用初始速度v1模拟冲击接触力，并和F1进行比较。

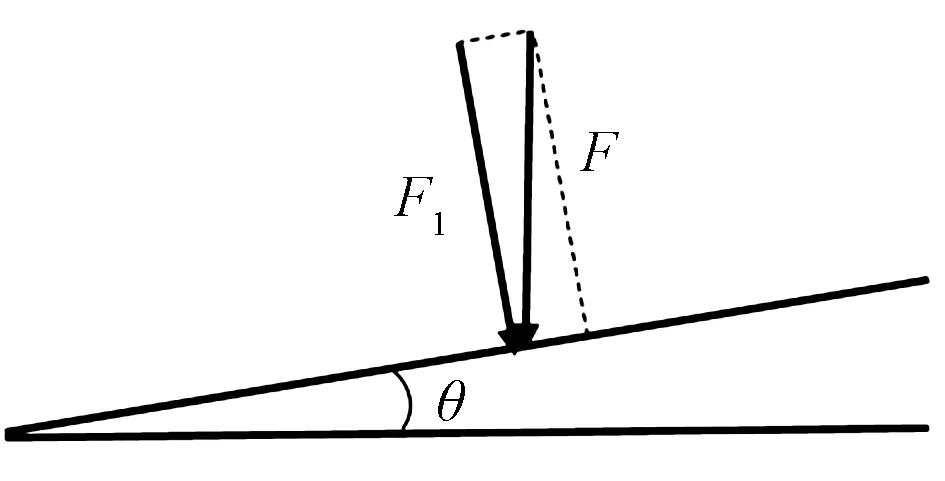
图5 冲击力示意图Fig.5 Diagram of impact force

图6 冲击速度示意图Fig.6 Diagram of impact velocity

对两种不同厚度的面板进行斜冲击测试，冲击能量设为1.51 J左右和3.84 J左右，通过改变试验件支撑组件的角度，可以得到不同冲击角度下的接触力。图7、图8和图9为0.5 mm厚面板的夹层复合材料在冲击角度为10°、20°和30°下的测试和仿真结果。实验后，通过观察发现夹层板的面板纤维发生断裂，可以发现在该种情况下，实验测得的力信号波动较为剧烈，特别是在下降阶段，这种现象更为明显。另外一方面，在图7中，可以发现两种方法得到的接触力信号模拟情况较好，但是在图8和图9中，冲击开始阶段模拟结果与实测结果吻合较好，随后实测冲击力的幅值低于模拟冲击力的幅值，这主要是由于当斜向冲击时，冲击头受到面板的侧向作用力，发生偏转所导致的；另外，斜向冲击对面板造成的损伤面更大一些，也会导致载荷的差异，而模拟时不会考虑这种因素。

图7 实验和仿真的接触力(hf=0.5 mm，E=1.51 J，θ=10°)Fig.7 The experimental and simulated force (hf=0.5 mm，E=3.84 J，θ=10°)

图8 实验和仿真的接触力(hf=0.5 mm，E=1.51 J，θ=20°)Fig.8 The experimental force and simulation force (hf=0.5 mm，E=1.51 J，θ=20°)

图9 实验和仿真的接触力(hf=0.5 mm，E=1.48 J，θ=30°)Fig.9 The experimental and simulated force (hf=0.5 mm，E=1.48 J，θ=30°)

0.8 mm厚面板在冲击能量为3.84 J左右，冲击角度分别为10°、20°、30°的情况下，测量和仿真的接触力分别如图10、图11和图12所示。由于试验件面板较厚，试验件表面均未出现明显的面板纤维损伤的情形。

图10 实验和仿真的接触力(hf=0.8 mm，E=3.84 J，θ=10°)Fig.10 The experimental and simulated force (hf=0.8 mm，E=3.84 J，θ=10°)

图11 实验和仿真的接触力(hf=0.8 mm，E=3.82 J，θ=20°)Fig.11 The experimental and simulated force (hf=0.8 mm，E=3.82J，θ=20°)

图12 实验和仿真的接触力(hf=0.8 mm，E=3.84 J，θ=30°)Fig.12 The experimental and simulated force (hf=0.8 mm，E=3.84 J，θ=30°)

通过对比图10、图11、图12可以发现，当冲击能量为3.84 J左右时，随着冲击角度的增加，冲击接触力的最大值不断减小。冲击角度分别为10°、20°、30°的时候，最大冲击力分别约为662、548、466 N，呈现规律性地减小。随着冲击角度的增大，理论模拟的精度也越来越差。当冲击角度增大的时候，冲头在冲击过程中，除了垂直于面板方向的运动以外，还可能在面板上滑动。而冲击角度越大，这种现象越明显，而仿真模型中没有考虑这个因素，因而仿真精度也随着角度的增大而降低。

4 材料参数对接触力的影响

4.1 面板的等效刚度

当面板厚度为0.5 mm时，其等效刚度为0.75 N·m;当厚度分别为0.44、0.5、0.56、0.63 mm时，对应的等效刚度分别为0.5、0.75、1、1.5 N·m，仿真得到的接触力如图13所示。可以看出，面板刚度对冲击响应的影响明显：随着面板的等效刚度的增加，冲击持续时间减小，冲击接触力的最大值增大。另外，由于面板的分层阈值与厚度有关，在仿真过程中，对应的面板的分层阈值力也随之调整。

图13 面板的等效刚度的影响Fig.13 The influence of effective stiffness of face sheet

4.2 芯材的模量

图14 芯材模量的影响Fig.14 The influence of modulus of core

4.3 芯材的压缩强度

实验所用芯材的压缩强度Pu为1.7 MPa，这里又计算了芯材的压缩强度为0.5、1、2.2 MPa时的接触力，如图15所示。可以发现，芯材的压缩强度对冲击力形态影响较大，压缩强度增大的时候，接触力峰值会增大，相应地，冲击周期会变小。这主要是由于当面板受到冲头冲击的时候，压缩强度较大的芯材能够达到更大的位移而不产生损伤，因此根据接触力的公式，接触力和凹坑深度成正比，因此接触力峰值会更大。

图15 芯材压缩强度的影响Fig.15 The influence of the compressive strength of the core

4.4 芯材的厚度

根据式(7)和式(8)，芯材厚度存在一个临界参考值hcmax，当芯材厚度hc大于hcmax时，材料为薄面板蜂窝夹层复合材料，而当芯材厚度hc小于hcmax时，应采用不同的模型参数计算式，在本项仿真研究中，hcmax值为7 mm。分别选取芯材厚度为3、6、14、20和25 mm，仿真得到的接触力曲线如图16所示。

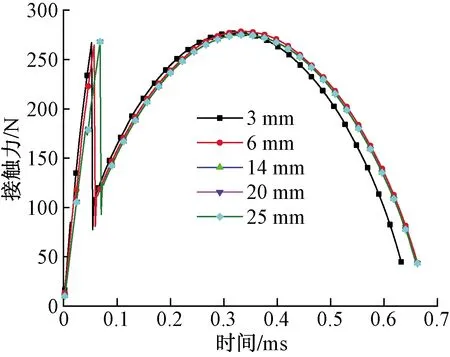
图16 芯材厚度的影响Fig.16 The influence of core thickness

从图16中可以看出，当蜂窝芯材厚度改变的时候，力曲线的最大值几乎不发生改变。根据式(4)，当芯材厚度小于hcmax时，芯材厚度会影响芯材压溃力，当芯材厚度为3 mm时，压溃力大约为83 N，而6 mm芯材的压溃力为107 N。此外，当芯材厚度超过hcmax时，即当芯材厚度分别为14、20、25 mm时，冲击周期有所增大，但各个接触力曲线几乎完全重合，因此对于薄面板蜂窝夹层材料，如果仅仅是芯材厚度不同，则冲击接触力变化不大。

5 结论

改进了小质量冲击试验机，使其能够产生不同角度下的斜冲击。使用该设备对蜂窝夹层复合材料进行不同角度和不同速度的冲击试验。在已有的蜂窝夹层复合材料小质量冲击工程算法基础上，增加面板刚度折减模型，模拟由于面板分层导致的弯曲刚度下降。得到以下结论。

(1)在受到外来小质量物体冲击的时候，蜂窝夹层复合材料会依次出现芯材压溃、面板分层、面板纤维断裂以及穿透损伤。

(2)基于所提出的刚度折减方法仿真不同角度和不同速度下的冲击力曲线，所得结果和实测结果趋势吻合，表明了所用方法的有效性。

(3)参数分析表明，面板的等效刚度和芯材的压缩强度对冲击周期和最大冲击接触力具有较大的影响，而芯材的厚度和模量则对冲击周期和冲击接触力的影响较小。