Cross-sectional deformation of H96 brass double-ridged rectangular tube in rotary draw bending process with diあerent yield criteria

Yangyang XIA, Yuli LIU,*, Mengmeng LIU

a Research & Development Institute of Northwestern Polytechnical University in Shenzhen, Shenzhen 518057, China

b State Key Laboratory Solidification Process, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

KEYWORDS Anisotropy yield criterion;Cross-sectional deformation;H96 double-ridged rectangular tube;H-type rotary draw bending;Inverse method

Abstract Different yield criterion has great difference in predicting the deformation of tube with different material.In order to improve the prediction accuracy of the cross-sectional deformation of the double-ridged rectangular tube(DRRT)during rotary draw bending(RDB)process,Mises isotropic yield criterion, Hill’48 and Barlat/Lian anisotropic yield criteria commonly used in practical engineering are introduced to simulate RDB of DRRT.The inverse method combining uniaxial tensile test of whole tube and response surface methodology was proposed to identify the parameters of Hill’48 and Barlat/Lian yield criteria of small-sized H96 brass extrusion DRRT as well.Then based on ABAQUS/Explicit platform, the FE models of RDB process of DRRT considering Mises,Hill’48 and Barlat/Lian yield criteria were built. The results show that: The variation trend of cross-sectional deformation ratio is same when using different yield criteria. The cross-sectional deformation ratio by using Mises yield criterion is close to that by using Hill’48 yield criterion.However,there is a quite difference between by using Barlat/Lian yield criterion and by using Mises or Hill’48 yield criteria. The prediction values of cross-sectional height deformation by using three yield criteria all underestimate the experiment ones, and the prediction values of cross-sectional width deformation overestimate the experiment ones. By comparing the simulation results of cross-sectional deformation of the DRRT with different yield criteria and experiment ones, Barlat/Lian yield criterion is found to be suitable for describing the RDB process of DRRT.

1. Introduction

Due to the merits of wider operation bandwidth, lower characteristic impedance and lower cutoff frequency, the bent double-ridged rectangular tube (DRRT) has been widely applied in the fields of the microwave communication, radar and electronic countermeasure.1Rotary draw bending (RDB)is commonly used to manufacture DRRT bending parts because of its high bending accuracy, stable forming quality and high productivity.2However, the RDB of DRRT is a high-nonlinearity complex physical process, and defects such as cross-sectional deformation, springback and wrinkling occur easily during RDB process. Moreover, the crosssectional deformation will seriously affect the microwave transmission efficiency, so controlling it becomes a prime priority to improve the precision of DRRT during RDB process. The FE simulation method has been widely used in tube bending research because of its simplicity, high efficiency and accuracy. However, since the tube is generally formed by drawing, extrusion, rolling, etc., which appears to be obvious anisotropy. In order to improve the prediction accuracy of the cross-sectional deformation of DRRT during RDB process, it is very important to select the yield criterion that can accurately describe the anisotropic behavior of the material. Therefore, it is of great significance to study the influence of different yield criteria on prediction accuracy of the cross-sectional deformation of RDB process of DRRT.

At present,domestic and foreign scholars have done a lot of research about the influence of yield criterion on the prediction accuracy of cross-sectional deformation of bending tube.Miller and Kyriakides3used Mises isotropic yield criterion to simulate the bending process of aluminum alloy rectangular tube, the results showed that the prediction value of crosssectional deformation of the tube was seriously underestimated by about 30%. Zhu et al.4introduced Mises, Hill’48 and Barlat91 yield criteria into the bending process of 304 austenitic stainless steel tube, the parameters of these yield criteria were determined by uniaxial tensile tests at 0°, 45° and 90°. Then by comparing section flatness of tube, it was found that the simulated value obtained by Hill’48 yield criterion is more consistent with the experimental value. Hopperstad et al.5obtained the parameters of Hill’48 and Barlat/Lian yield criteria by uniaxial tensile tests at 0°, 45° and 90°, and the above yield criteria were introduced into the bending process of tube,then found that the latter is more accurate for predicting the height deformation of the bending tube. From the above research, different yield criteria have great difference in predicting the deformation of different material tubes. So far,no one yield criterion is suitable for forming process of all material tubes. Moreover, the parameters of the anisotropic yield criterion in the above literatures are determined directly by using uniaxial tensile tests with different angles of tube extrusion direction.

H96 brass DRRT widely used in microwave transmission is small in size and has many edges, so it is difficult to determine the parameters of the anisotropic yield criterion by using uniaxial tensile tests at 45° and 90° with respect to tube extrusion direction. However, the reverse method is to obtain the material parameters backwardly by using FE method to simulate the deformation process of the specimen, and restrictions on the size and deformation of the specimen are relaxed,6therefore, the reverse method is widely applied to determine parameters of anisotropic yield criterion. Yan et al.7determined the parameters of Hill’48 yield criterion of low carbon steel by the inverse method combining plate bending test and orthogonal experiment,and discovered that Hill’48 yield criterion can better describe the deformation behavior of plate during roll bending.Because it is difficult to obtain the specimen that meets the dimensional requirements, Liu et al.8obtained the strength coefficient and hardening exponent of steel tube by the reverse method and flattening test. And the reliability of the reverse parameters was verified by the tube collision test. Chamekh et al.9adopted the inverse method combining the cylindrical cup drawing test to obtain the parameters of the steel’s Hill’48 yield criterion. The result showed that Hill’48 yield criterion determined by the reverse method can well describe the earing phenomenon. Material performance parameters in the above studies were obtained based on the inverse method combining the actual forming process, and the reliability of the reverse parameters was verified by experiment. However, a large number of iterative calculations were required in the reverse process, resulting in lower efficiency. In order to improve the efficiency of determining parameters of yield criterion, inverse method combining response surface methodology (RSM) was proposed,10in which the FE simulations can be executed simultaneously and iterations can be avoided, so the computing time was reduced sharply.

Moreover, the accuracy of parameters of yield criterion is largely determined by the suitability of experimental measurements in the inverse method. Two commonly used methods to determine the parameters of anisotropy yield criterion are based on yield stresses and r-values, respectively. Xue and Liao11determined the parameters of Hill’48 yield criterion by the above two methods of DC05 steel plate, the result showed that Hill’48 yield criterion determined by r-values could describe in-plane principal strain and outline of cross-die deep drawing specimen better. Wang et al.12found the earing phenomenon of 5754O aluminum alloy can be predicted well by Hill’48 yield criterion based on r-values. The above studies showed that the parameters of yield criterion through r-values was more suitable for describing the workpiece deformation problem. Our research group13-16has done a lot of research about the crosssectional deformation of H96 brass DRRT in H-typed bending and E-typed bending by the FE method. The establishment of the FE models are based on Mises isotropic yield13-15and Hill’48 anisotropy yield criterion,16while the parameters of Hill’48 yield criterion are determined based on stress measurements.

Therefore, in order to confirm the yield criterion which is suitable for predicting the cross-sectional deformation of RDB process of H96 brass DRRT,Mises isotropic yield criterion, Hill’48 and Barlat/Lian anisotropic yield criteria widely used in practical forming are selected and the parameters of Hill’48 and Barlat/Lian anisotropic yield criteria are determined based on deformation measurements in inverse method combining RSM. The prediction accuracy of the three yield criteria on the cross-sectional deformation of RDB process of DRRT was evaluated by comparing simulation results and experiment ones.

According to the BBD method,three levels are selected for each parameter.And the three levels value of each parameter is determined as shown in Table 1.Therefore,17 FE simulations of uniaxial tensile test of DRRT need to be executed as shown in Table 2.Fig.3 shows the specimen and FE model of uniaxial tensile test of H96 brass DRRT,and the mechanical parameters of H96 brass DRRT obtained by uniaxial tensile test were shown in Table 3.The constitutive equation in Eq.(14)is used to describe the plastic deformation of DRRT.

The 17 FE simulation results of the uniaxial tensile test of DRRT are also recorded in Table 2.Based on these simulation results, the mathematical models (Eq. (10)) relating three responses ΔW10, ΔW20and ΔW25to the parameters R22, R33and R12were established, as shown in Eqs. (15)-(17):

Table 1 Three parameters R22, R33 and R12 and their respective levels.

So the objective function is constructed by substituting Eqs.(15)-(17)into the Eq.(11).Then the value of R22,R33and R12can be determined by minimizing the objective function shown in Eq. (11). And the parameters of Hill’48 yield criterion can be obtained by plugging value of R22, R33and R12into Eq.(8), as shown in Table 4. The parameters of Barlat/Lian yield criterion can be determined by using same method,as shown in Table 4 too.

3. Influence of yield criteria on prediction accuracy of crosssectional deformation of DRRT

3.1. Description of cross-sectional deformation and selection of characteristic section of DRRT

Fig. 4(a) shows the section of tube before and after deformation. In order to describe the cross-sectional deformation of the DRRT during RDB process,Eqs.(18)-(21)are introduced to describe the different part deformation of characteristic sections.

where ΔHiand ΔBiare the height and width deformation ratio of the tube, respectively, and Δhiand Δbiare the height and spacing deformation ratio of ridge groove of tube,respectively.H and B are the values of height and width of cross-section,while h and b are the values of height and spacing of ridge groove before bending deformation. Hi, Bi, hiand biare the corresponding values after bending deformation.

Meantime,in order to systematically study the effect of different yield criteria on the cross-sectional deformation of tube,the two characteristic sections along the bending direction are selected as shown in Fig.4(b),which are section S2 in the mandrel support zone and section S6 in the non-mandrel support zone.And the distribution of nodes along the height and width direction on characteristic section has been given in Fig. 5(a)and (b).

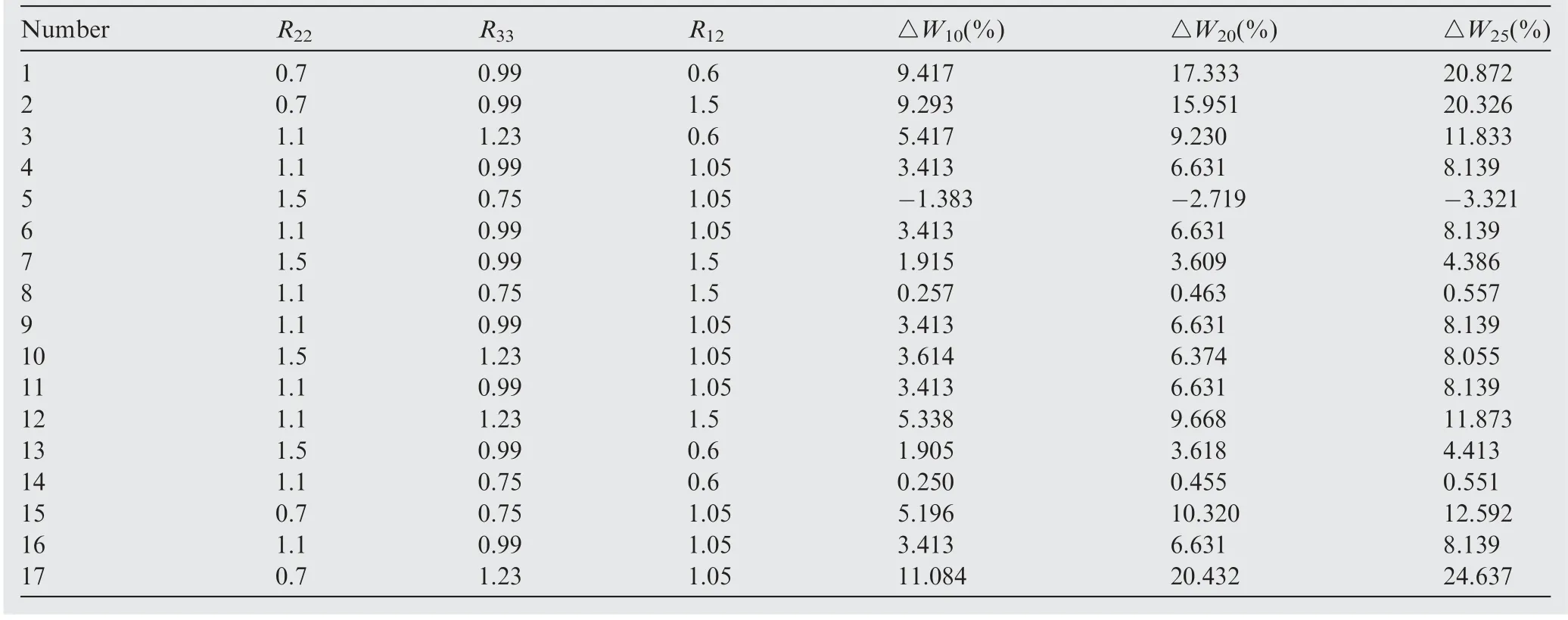
Table 2 The experiment arrangement of BBD and the simulation results of response.

Fig. 3 Specimen and FE model of uniaxial tensile test of DRRT.

Table 3 Mechanical parameters of H96 brass double-ridged rectangular tube.

Table 4 Parameters of Hill’48 and Barlat/Lian yield criteria determined by the inverse method.

3.2. Establishment of FE model of RDB process of DRRT

Based on the mechanical properties of the H96 brass DRRT in Table 3 and the parameters of yield criterion in Table 4, the constitutive models of different yield criteria of H96 brass DRRT are constructed and introduced in the FE model. In order to improve the computational efficiency and accuracy of the FE model, the rigid dies are modeled with 4-node 3D bilinear quadrilateral elements C3D4, meantime the tube is defined as deformable body and described by 4-node doubly curved thin shell elements S4R. And mesh sizes of tube and mandrels are all 1 mm×1 mm, the other rigid dies are 3 mm×3 mm. The friction between tube and dies is modeled with classical Coulomb friction model. Based on the above solved key technologies, the RDB process of DRRT is carried out based on ABAQUS/Explicit, the springback process of DRRT is carried out based on ABAQUS/Standard, and the established FE models considering different yield criteria are shown in Fig. 6. And the tube bender and dies for RDB process are shown in Fig. 7. The process parameters of RDB of DRRT in FE simulation and experiment are shown in Table 5.

3.3. Deformation analysis of characteristic section of DRRT during RDB with different yield criteria

3.3.1. Analysis of height deformation ratio of characteristic section

Fig. 8 shows the distribution of the height deformation of characteristic sections S2 and S6 with Mises, Hill’48 and Barlat/Lian yield criteria.It can be seen that no matter which yield criterion is employed, the height deformation ratio (ΔHi) of characteristic section is symmetrical about the centerline 5-5′(Fig. 5(a)) and presents the variation trend of the ‘‘M” type.ΔHiis all negative values with the three yield criteria, which shows that the inner and outer flanges of the tube have collapsed during RDB process.The height deformation of section S6 is greater than that of section S2 for different yield criteria.ΔHiby using Mises yield criterion is close to that by using Hill’48 yield criterion. However, ΔHiby using Barlat/Lian yield criterion is quite different from ΔHiby using Mises and Hill’48 yield criterion,and prediction value of the height deformation of DRRT by using Barlat/Lian yield criterion is maximal, which is minimal when using Hill’48 yield criterion.

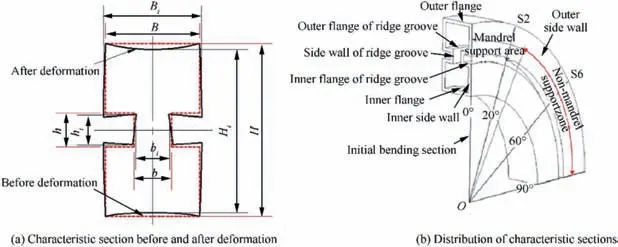
Fig. 4 Sketch of characteristic section before and after deformation and position of characteristic section.

Fig. 5 Distribution of nodes on characteristic section.

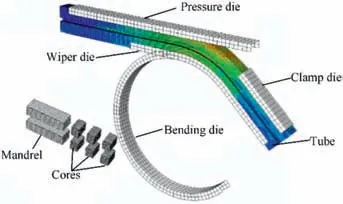
Fig. 6 FE model for RDB of DRRT.

3.3.2. Analysis of height deformation ratio of ridge groove of characteristic section

Distribution of the height deformation of ridge groove in sections S2 and S6 with Mises, Hill’48 and Barlat/Lian yield criteria has been shown in Fig.9.The height deformation of ridgegroove of section S6 is bigger than that of section S2 with the different yield criteria.The height deformation of ridge groove ratio (Δhi) is also systematical about the centerline 5-5′and presents the variation trend of inverse‘‘V”type.Δhiis all negative values with these three yield criteria, which shows that the height of ridge groove produced compression deformation,

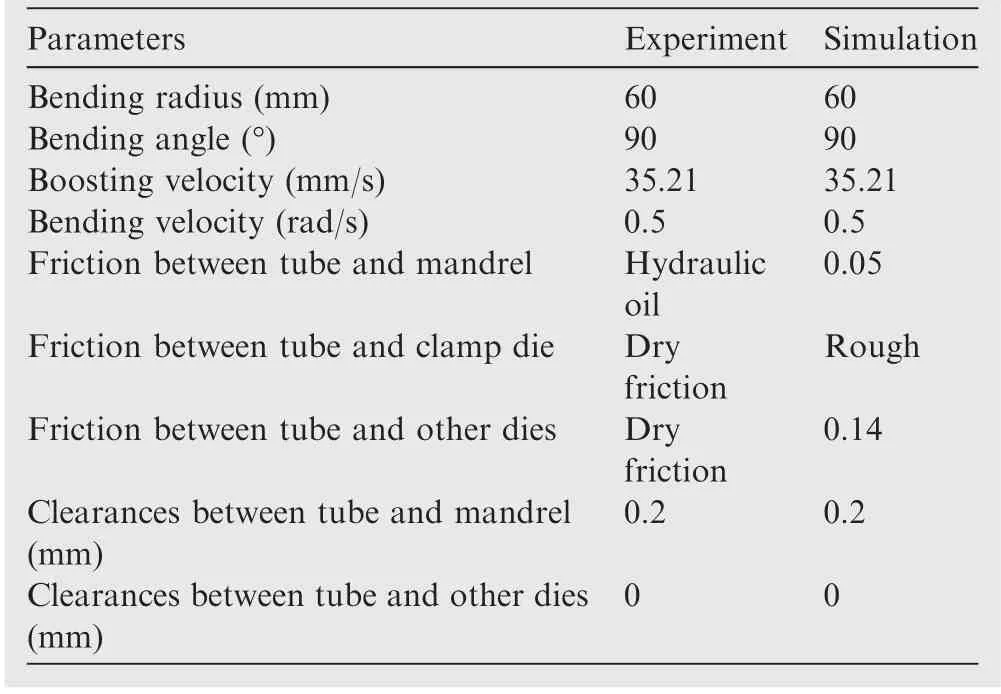
Table 5 Process parameters of RDB of DRRT.

Fig. 7 Tube bender and dies.

Fig. 8 Distribution of the height deformation ratio of sections S2 and S6 with different yield criteria.

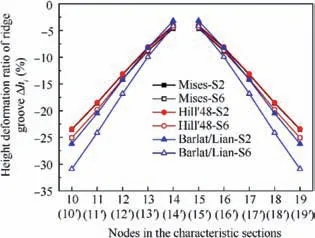
Fig. 9 Distribution of the height deformation ratio of ridge groove of sections S2 and S6 with different yield criteria.

and maximum Δhiis located at nodes 10(10’) and 19(19’),namely at the opening of ridge grooves. This is because the ridge groove is not directly supported by the mandrel, and its stiffness is insufficient during bending process, the ridge groove is severely deformed by radial extrusion from the sidewall of the tube. Like the law of cross-sectional height deformation ratio, the height deformation ratio of ridge groove of characteristic section is very close with Mises and Hill’48 yield criteria, and which is biggest with Barlat/Lian yield criterion.

3.3.3. Analysis of width deformation ratio of characteristic

section

Fig.10 shows the distribution of the width deformation of sections S2 and S6 with different yield criteria. The width deformation ratio (ΔBi) of characteristic section is all negative values with three yield criteria, which shows that the area also produced compression deformation,and width deformation of characteristic section in the outer side of neutral layer is larger than that in the inner side of neutral layer.The absolute value of ΔBiin the outer side of neutral layer from node 20(20′) to node 28(28′) increases after an initial decrease, the maximum deformation is located at node 28(28′), namely the ridge of the outer flange of the ridge groove. The absolute value of ΔBiin the inner side of neutral layer from node 34(34′)to node 42(42′)also increases after an initial decrease,the maximum is reached at node 34(34′), namely the ridge of the inner web of the ridge groove.In conclusion,the maximum width deformation of characteristic section is located at the intersection of side wall and ridge groove. This is because the ridge groove part has been undergone severe contraction deformation during bending process, and the inner and outer flanges of ridge groove collapsed. Due to the deformation coordination effect,the sidewall of the tube is also greatly deformed. ΔBiby using Mises yield criterion is very close to that by using Hill’48 yield criterion, and prediction value of the width deformation of characteristic section by using Mises and Hill’48 yield criteria is bigger than that by using Barlat/Lian yield criterion.

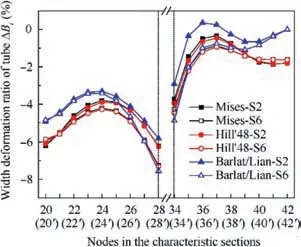
Fig. 10 Distribution of the width deformation ratio of sections S2 and S6 with different yield criteria.

3.3.4. Analysis of spacing deformation ratio of ridge groove of characteristic section

Distribution of the spacing deformation of ridge groove of sections S2 and S6 with different yield criteria has been shown in Fig.11.The spacing deformation ratio of ridge groove of characteristic section(Δbi)is all negative values with three yield criteria, which shows that spacing of ridge groove produced compression deformation. The absolute value of Δbifrom node 29(29′)to node 33(33′)decreases after an initial increase,the maximum is reached at node 30(30′) which is more than 14%. Due to no-mandrel filling, spacing of ridge groove of tube has undergone severe deformation during bending process. Spacing deformation of ridge groove of section S2 with Barlat/Lian yield criterion are smaller than with Mises and Hill’48 yield criteria, and spacing deformation of ridge groove of section S6 with Barlat/Lian yield criterion are larger than with Mises and Hill’48 yield criteria. Regardless of section S2 or section S6, the predicted values of the spacing deformation of ridge groove are close with Mises and Hill’48 yield criteria.

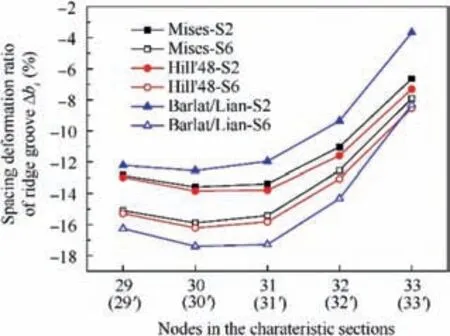
Fig. 11 Distribution of the spacing deformation ratio of ridge groove of sections S2 and S6 with different yield criteria.

3.4. Applicability evaluation of three yielding criteria for describing cross-sectional deformation of DDRT

In order to evaluate the accuracy of the cross-sectional deformation of DRRT predicted by different yield criteria, Fig. 12(a) shows the experimental result of the DRRT bent part adopting conditions shown in Table 5, and Fig. 12(b), (c)and (d) gives simulation results of the DRRT bent part by using different yield criteria under the same conditions. From Fig. 12, it can be qualitatively found that the tube bent by experiment is coincide with the tube bent by using different yield criteria. However, from this figure, it is difficult to directly judge from the intuitional shape which yield criterion is suitable for describing the cross-sectional deformation of DRRT.So Fig.13 shows the quantitative experiment and simulation results corresponding to Fig. 12, which is crosssectional height deformation located at node 1(1′) and crosssectional width deformation located at node 20(20′) along the bending direction.

From Fig. 13(a), it can be seen that the variation trend of cross-sectional height deformation of tube is almost same by using different yield criteria,and the predicted values by using these three yield criteria all underestimate the cross-sectional height deformation of the DRRT. The predicted values with Mises and Hill’48 yield criterion are very close, which are different from that with Barlat/Lian yield criterion, but the predicted value with Barlat/Lian yield criterion are the closest to the experimental values.The average relative errors between experiment value and simulated values of Mises, Hill’48 and Barlat/Lian yield criteria are 14%, 14.1% and 6.8%, respectively. It is visible that Barlat/Lian yield criterion can better predict the cross-sectional height deformation of the DRRT.

From Fig. 13(b), it can be seen that the variation trend of cross-sectional width deformation of tube is also same by using different yield criteria. Different from the height crosssectional deformation,the predicted values by using three yield criteria all overestimate the width cross-sectional deformation of the DRRT, and the predicted values by using Barlat/Lian yield criterion are the closest to the experimental values among three yield criteria, the average relative errors is only 4.8%.However,the average relative errors between simulated values by using Mises and Hill’48 yield criteria and experiment value are 26.5%and 23.9%,respectively, and the maximum relative errors of the experiment and simulation values by using these two yield criteria reach up to 35.8%and 32.5%,respectively.It can be seen that Mises and Hill’48 yield criteria have a poor simulation precision for the cross-sectional width deformation of H96 brass DRRT,and Barlat/Lian yield criterion can better predict cross-sectional width deformation of the DRRT.

Fig. 12 DRRT bent comparison of simulation results by using different yield criteria and experiment result.

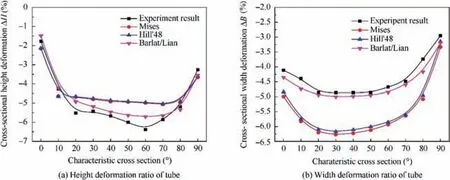
Fig. 13 Simulation results of cross-sectional deformation with three yield criteria and experiment result.

From the above analysis,it can be seen that different yielding criteria have different prediction accuracy for the crosssectional deformation of DRRT, which is mainly caused by the difference of yield criterion in describing plastic anisotropic behavior and predicting the shape of yield locus.5In order to further analyze the differences of predicting the crosssectional deformation of the DRRT by using different yield criteria, the r-value distribution and yield function shape of Mises, Hill’48 and Barlat/Lian yield criteria are given in Fig.14.Compared with Mises yield criterion,the plastic anisotropy of the material is considered by Hill’48 yield criterion,but the difference between the functional shapes of two yield criteria is small, which leads that the prediction values of cross-sectional deformation of the DRRT are relatively close.From Fig. 14(a), it can be seen that the difference of normal anisotropy r-value of the Hill’48 and Barlat/Lian yield criteria is small in different directions,but the functional shapes of the two yield criteria are quite different (as shown in Fig. 14(b)),which leads to a larger difference in the predicted value of the cross-sectional deformation of the DRRT.Therefore,compared with the anisotropy r-value,the difference of yield locus can be used to better explain the difference of prediction accuracy of cross-sectional deformation of DRRT.

The different yielding criteria have different prediction accuracy for the cross-sectional deformation of DRRT,which also can be explained from the tangential stress distribution of the tube bent by using different yield criteria, as shown in Fig. 15. Compared with Fig. 15(a) and (b), the distribution and magnitude of tangential stress of tube is very close by using Mises and Hill’48 yield criterion. But the distribution and magnitude of tangential stress of tube by using Barlat/Lian yield criterion as shown in Fig. 15(c) is obviously different from those as shown in Fig. 15(a) and (b).

In summary, the error between the experimental value and the simulated one by using Barlat/Lian yield criterion is the smallest, which can more accurately predict the crosssectional deformation of the DRRT among three yield criteria.

4. Conclusion

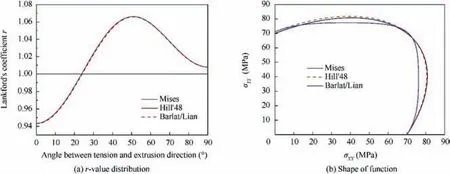
Fig. 14 r-value distribution and functional shape of the three yield criteria.

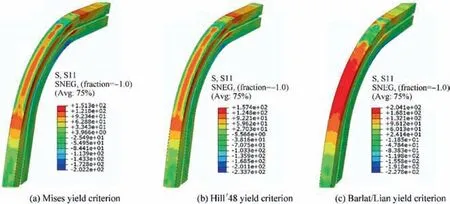
Fig. 15 Distribution of tangential stress of DRRT under different yield criteria.

(1) Mises,Hill’48 and Barlat/Lian yield criteria are selected to describe the RDB process of small-sized H96 brass DRRT, and the parameters of the Hill’48 and Barlat/Lian anisotropic yield criteria are obtained by using the inverse method combining uniaxial tensile test of whole tube and response surface methodology. On the basis of solving the key problems of model,3D FE models of DRRT considering different yield criteria are established.

(2) The variation trend of cross-sectional deformation ratio of tube is same when using different yield criteria.The deformation of each part of the characteristic section located in non-mandrel support zone is greater than that mandrel support zone. The cross-sectional deformation by using Mises yield criterion is close to that by using Hill’48 yield criterion. However, when using Barlat/Lian yield criterion,the cross-sectional deformation is greatly different.

(3) The prediction values of cross-sectional height deformation by using three yield criteria all underestimate the experiment ones, and the prediction values of crosssectional width deformation overestimate the experiment ones. The prediction values of cross-sectional deformation by Barlat/Lian yield criterion agree well with the experimental ones, while those by using Mises and Hill’48 yield criteria have a larger error with the experiment ones.

Acknowledgments

The research is supporting by the Science and Technology Project of Shenzhen of China(Nos.JCYJ20170306160003433 and JCYJ20180306171058717) and the National Natural Science Foundation of China (No. 51375392).