Application of a PCA-DBN-based surrogate model to robust aerodynamic design optimization

Jun TAO, Gng SUN, Liqing GUO, Xinyu WANG

a Department of Aeronautics & Astronautics, Fudan University, Shanghai 200433, China

b Department of Mechanical & Aerospace Engineering, University of California, Irvine 92697, USA

KEYWORDS Aerodynamic design optimization;Deep neural networks;Particle swarm optimization;Principal component analysis;Surrogate model

Abstract An efficient method employing a Principal Component Analysis(PCA)-Deep Belief Network (DBN)-based surrogate model is developed for robust aerodynamic design optimization in this study. In order to reduce the number of design variables for aerodynamic optimizations, the PCA technique is implemented to the geometric parameters obtained by parameterization method.For the purpose of predicting aerodynamic parameters, the DBN model is established with the reduced design variables as input and the aerodynamic parameters as output,and it is trained using the k-step contrastive divergence algorithm. The established PCA-DBN-based surrogate model is validated through predicting lift-to-drag ratios of a set of airfoils, and the results indicate that the PCA-DBN-based surrogate model is reliable and obtains more accurate predictions than three other surrogate models. Then the efficient optimization method is established by embedding the PCA-DBN-based surrogate model into an improved Particle Swarm Optimization (PSO) framework, and applied to the robust aerodynamic design optimizations of Natural Laminar Flow(NLF) airfoil and transonic wing. The optimization results indicate that the PCA-DBN-based surrogate model works very well as a prediction model in the robust optimization processes of both NLF airfoil and transonic wing. By employing the PCA-DBN-based surrogate model, the developed efficient method improves the optimization efficiency obviously.

1. Introduction

Aerodynamic design occupies a very crucial position in the research and development of a commercial aircraft. Over the past few decades, CFD has played an increasingly important role in aerodynamic design. For Aerodynamic Shape Optimization (ASO) problem, one of the main challenges is the expensive computational cost during the optimization process,which makes it prohibitive when a large number of highfidelity CFD simulations are required. Moreover, another key factor which affects the optimization efficiency is the number of design variables. When a large number of design variables are employed, the global searching efficiency of the optimization could be decreased obviously. Therefore, the development of efficient optimization methods for ASO problems of aircraft is of great interest and necessity.

Optimization methods based on CFD simulations can be classified into two categories1which are gradient-based methods and gradient-free methods. The gradient-based methods such as adjoint method usually converge very fast to obtain an optimization result, but these methods do not possess global searching ability and thus the solution often traps into a local optimum.2The gradient-free methods such as Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) are capable of obtaining global optimum,and are of great interest for ASO of aircraft.However,the computational cost of these methods could easily become prohibitive when high-fidelity CFD simulations are employed during the optimization process.

In order to reduce the computational amount of ASO,surrogate models have been developed to substitute for the highfidelity CFD simulations during the optimization process.Surrogate model is a type of approximation model which makes use of previously obtained sampling data in order to predict the values of objective functions at untried points. Different surrogate models have been developed and studied over the past few decades. There are mainly two categories3of surrogate models which are parametric (e.g., polynomial regression,4Kriging5) and non-parametric (e.g., projection-pursuit regression,6radial basis functions,7artificial neural network8)models. The parametric surrogate models assume that the global functional relationship of the response variable and the design variables is known, while the non-parametric surrogate models establish an overall model by using different types of simple, local models in different regions. Each surrogate model has different characteristics, and some comparisons among these surrogate models have been described in Refs. 3, 9-11.

Great efforts have been made to apply these surrogate models to the field of aerodynamic optimization in recent years,and positive results have been achieved. Jiang et al.12conducted the integrated optimization analyses of aerodynamic/stealth characteristics for helicopter rotor based on Radial Basis Functions(RBF)surrogate model,and obtained satisfied results by choosing suitable object function and constraint condition. Pehlivanoglu and Yagiz13completed aerodynamic optimizations for airfoil, multi-element airfoil and active flow control of airfoil by employing Response Surface Method(RSM) surrogate model, and their results indicated computational amount reductions of 50%, 70% and 50% respectively for these three optimizations. Tao and Sun14used Artificial Neural Network (ANN) surrogate model to predict aerodynamic parameters for the noise reduction optimization of a multi-element airfoil, and the results indicated that the surrogate model serves very well in predicting aerodynamic parameters. Han et al.15proposed the weighted gradient-enhanced Kriging surrogate model and applied it to the inverse design of a transonic wing. Their results indicated that the proposed surrogate model is much more efficient than the Kriging surrogate model without using any gradient,and thus is more practical for higher-dimensional problems. In addition, infill sampling criterion and constraint handling are important issues for SBOs(surrogate-based optimizations).Sasena et al.16reviewed several different infill sampling criteria, and investigated the effect of them on the optimization results. Zhang et al.17investigated three different constrained aggregation approaches for wing structural design, and combined them with an in-house SBO code within the framework of a gradient-free optimization. They concluded from their test cases that the most efficient way of handling large-scale constraints for wing SBO is to aggregate constraints within subdomains and with a relatively large constant parameter.

For the purpose of overcoming the shortcoming that too many design variables can decrease the optimization efficiency greatly,an effective way is to reduce the number of design variables via dimension reduction techniques.This can be realized by using Principal Component Analysis (PCA) technique.Asouti et al.18used the PCA technique to better guide the application of evolution operators and train metamodels in Metamodel-Assisted Evolutionary Algorithms (MAEAs). By reducing the design variables, the PCA-assisted method is applied to multi-objective,constrained,aerodynamic optimization problems. Wang et al.19developed a PCA-ANN-based inverse design model, and applied it to the stall lift robustness design for high-lift devices. Their results indicated that the design efficiency is improved obviously by using the PCAANN-based inverse design model. Since surrogate models are usually trained on the basis of a database, PCA technique can be implemented to the database to reduce design variables.It is very suitable and convenient to apply PCA technique to the SBOs discussed in this study, and thus the optimization efficiency is expected to be improved. Furthermore, by reducing the number of design variables, the number of samples needed for training the surrogate model can be reduced correspondingly.

Given the above, this study aims to develop an efficient method to improve the optimization efficiency of ASO problems of aircraft. On one hand, the PCA technique is used to reduce the number of design variables. On the other hand, a Deep Belief Network (DBN) surrogate model is built and trained on the basis of the reduced design variables to predict aerodynamic parameters during the optimization process.Then an efficient optimization method is established by embedding the well trained PCA-DBN-based surrogate model into an improved PSO algorithm, and applied to the robust aerodynamic design optimizations for Natural Laminar Flow(NLF) airfoil and transonic wing.

This paper is organized as follows. In Section 2, numerical methods and validations of the CFD code are introduced. In Section 3, an improved PSO algorithm is presented and validated. In Section 4, the PCA-DBN-based surrogate model is established and validated.In Section 5,applications of efficient optimization method to the robust aerodynamic design optimizations of NLF airfoil and transonic wing are performed.Finally, in Section 6, some conclusions are drawn according to the previous results and analyses.

2. Numerical methods and validation

In this study,the PCA-DBN-based surrogate model is applied to the robust optimizations of NLF airfoil and transonic wing.A Reynolds-averaged Navier-Stokes CFD code is employed for establishing the databases and validating the optimization results. The two-equation k-ω SST turbulence model20shown below is employed for turbulence simulation.

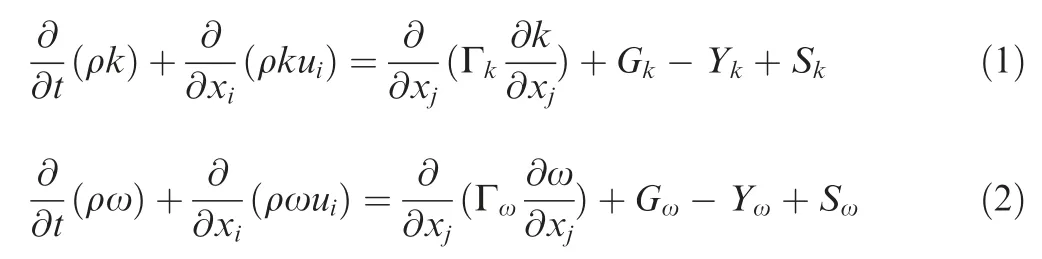
where the specific definitions of terms in these two equations are introduced in Ref. 20.

As for transition prediction,there are mainly two engineering applicable transition methods,which are eNmethod and γ-Reθttransition model-based method. eNmethod was firstly developed based on Linear Stability Theory (LST),21and has been successfully applied to transition location prediction of a flat plate. In order to address the problem existing in the LST/eNmethod, some improved methods have been developed. Wu et al.22proposed a High-Order Dynamic Mode Decomposition (HODMD)-based eNmethod, and used it to predict transition locations of airfoils. Their results indicated that the transition locations predicted by the HODMD/eNmethod agreed well with experimental data and were compared favorably to those obtained by some existing methods.γ-Reθttransition model23,24is a local correlation-based transition model which is described by an intermittency factor (γ)equation and a momentum thickness based Reynolds number(Reθt) equation. For the NLF airfoil optimization case in this study, the γ-Reθttransition model is adopted. The γ equation and Reθtequation are described as

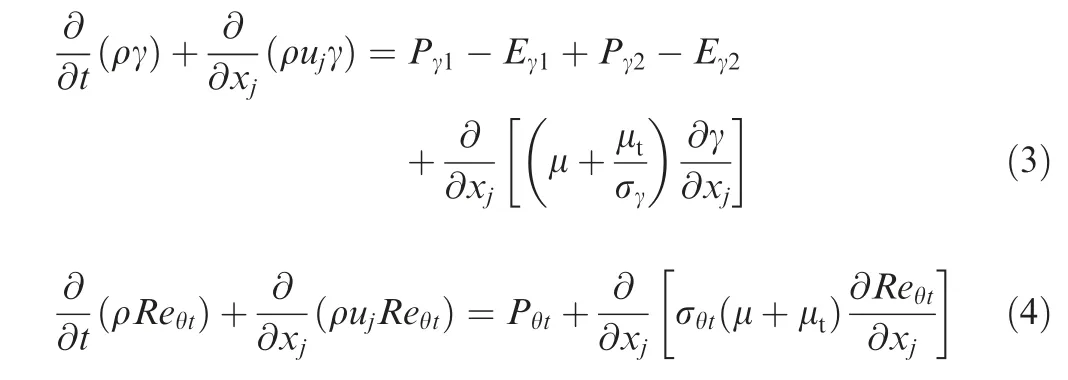
where specific definitions of source terms in these two equations are introduced in Ref. 23.

In order to validate the reliability of the CFD code,numerical simulations are conducted to the NLR7301 airfoil and the DLR-F6 wing-body model.

Fig. 1 shows three computational grids around NLR7301 airfoil, which are coarse grid, medium grid and fine grid,respectively. Table 1 shows the node number and average Y+ of the three grids. For the purpose of investigating mesh convergence, numerical simulations are conducted based on these three grids. Computational conditions are set as:Ma=0.748， Re=2.2×106.

Fig. 2 shows the lift and drag coefficients (CLand CD)obtained by CFD simulations on the basis of the three grids compared with those by experiments.25As can be seen, the computational results from the fine grid are better than those from the other two grids,and are very close to the experimental results. Therefore, the fine grid is selected for further validating computations.

Fig. 1 Computational grids around NLR7301 airfoil.

Table 1 Node number and average Y+ of three grids.

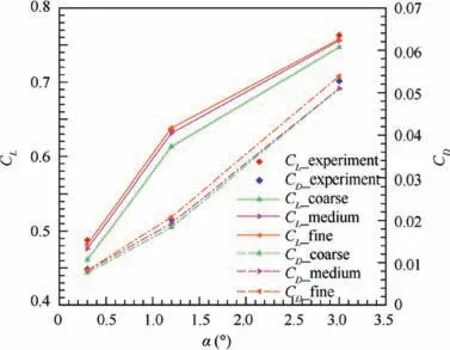
Fig.2 Computational lift and drag coefficients on basis of three grids compared with those by experiments.25

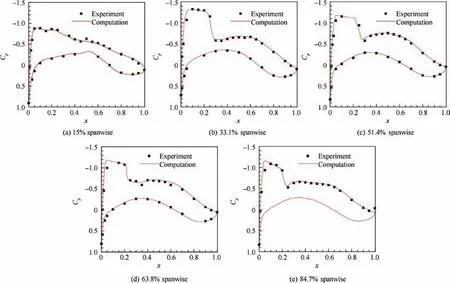
Fig. 6 Comparison of pressure coefficients distribution at different spanwise locations.

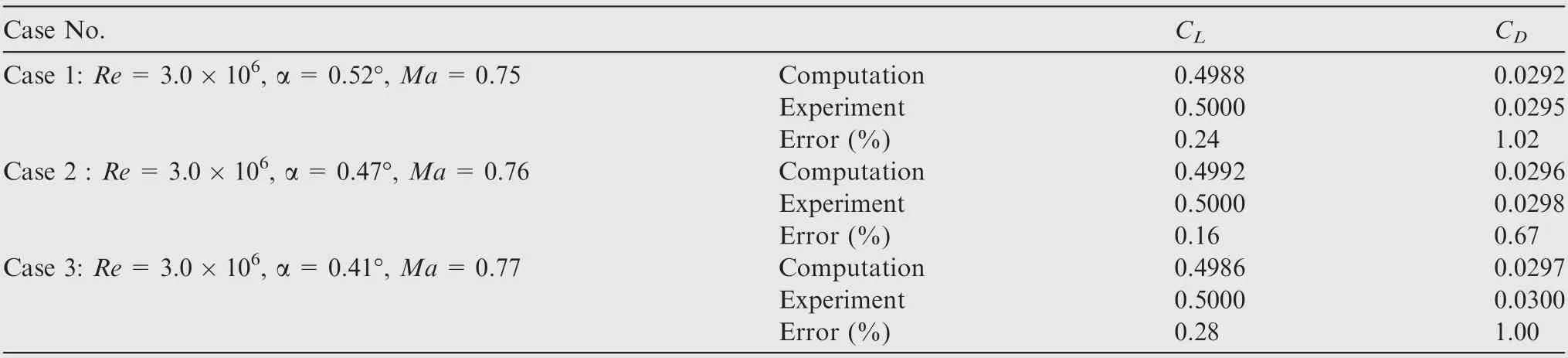
Table 2 Comparison of aerodynamic coefficients for DLR-F6 wing-body.

Fig. 8 shows original positions of the particles with LHS method compared to those without LHS method. As can be seen,original positions of the particles are generated more dispersedly and reasonably by adopting LHS method, which can lead to a faster convergence rate and improved optimization results.

Besides adopting LHS method, a second-order oscillating scheme and an FDR item are employed to update velocities and positions of the particles. The velocity and position of each particle are updated as

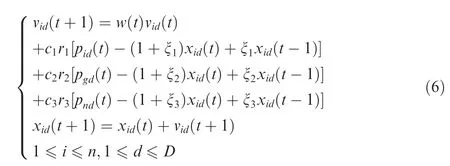
where ξ1, ξ2and ξ3are random numbers.c3r3［pnd（t）-（1+ξ3）xid（t）+ξ3xid（t-1）］ is called FDR item,and

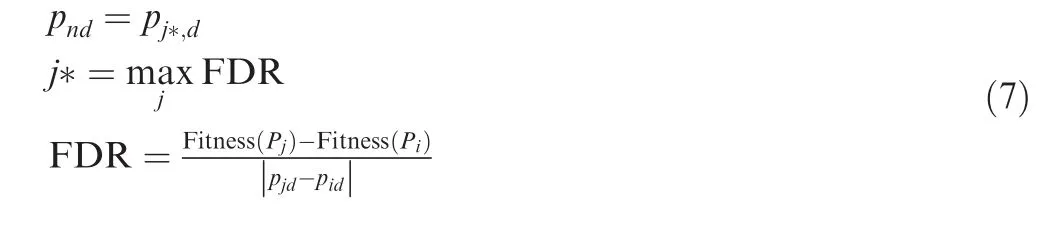
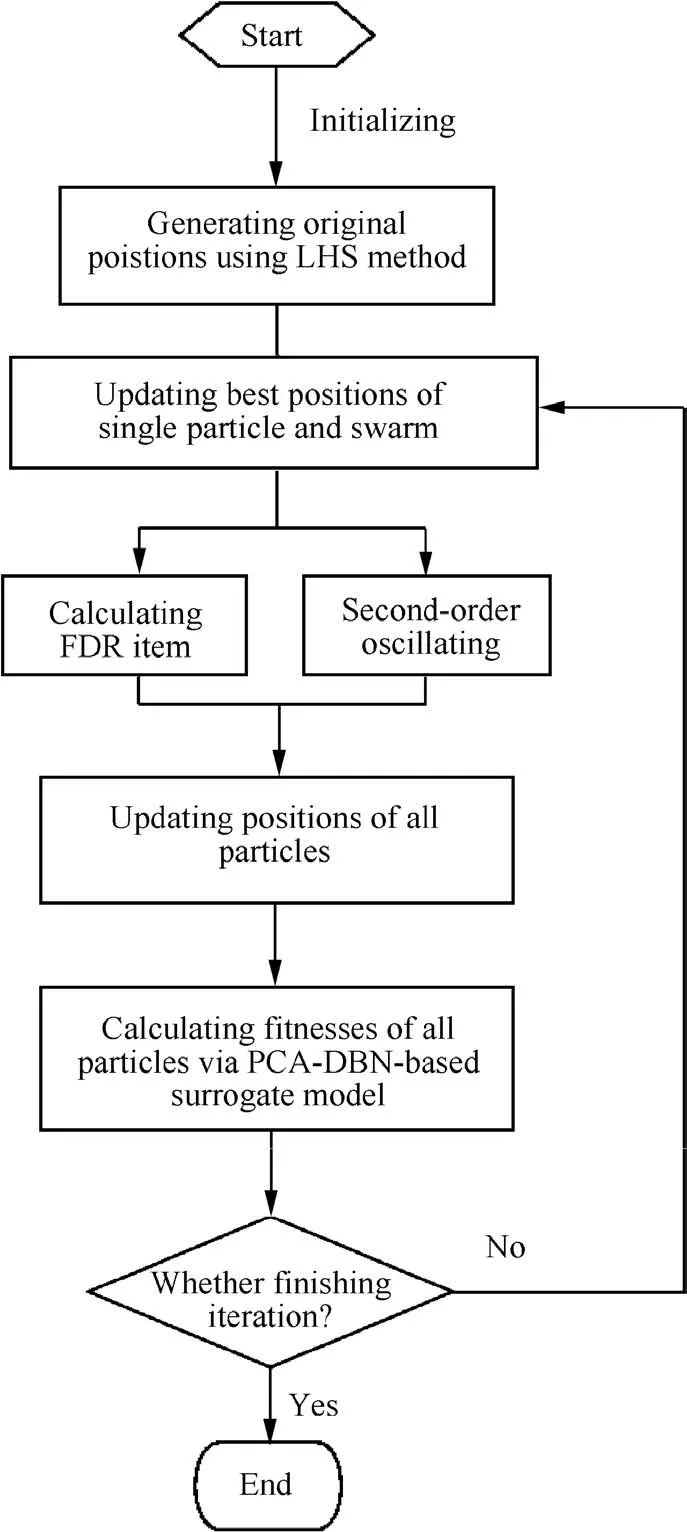
Fig. 7 Process of LHS-FDR-SOPSO algorithm.

The value of FDR refers to the ratio between the fitness difference and the distance from the ith particle to the jth particle.By introducing the FDR item,the position of the ith particle is updated to approach the j*th particle with the maximum FDR in the iteration.

In order to enable the improved PSO algorithm to have strong global searching ability and fast convergence rate, ξ1,ξ2and ξ3are assigned as the following rules:

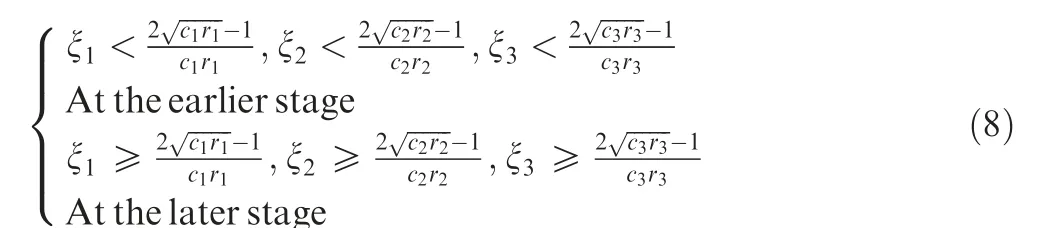
For the purpose of balancing global and local searching abilities, the inertia weight factor w is set to vary as follows:

where T is the maximum iterations, winitialis the initial inertia weight factor, and wfinalis the final inertia weight factor at the last iteration. In this study, winitialand wfinalare set to be 0.9 and 0.4, respectively.

In order to validate the optimization efficiency of LHS-FDR-SOPSO algorithm, Griewank function shown in Eq. (10) is selected to test its performance.

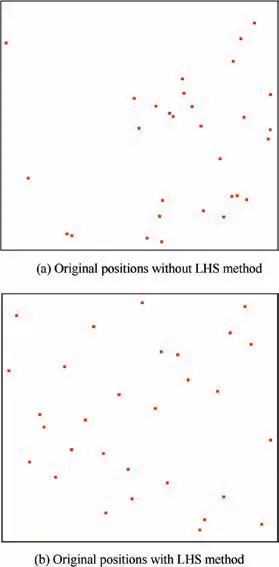
Fig. 8 Original positions with LHS method compared to those without LHS method.

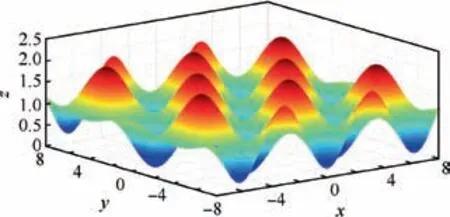
Fig. 9 Spatial surface of Griewank function.

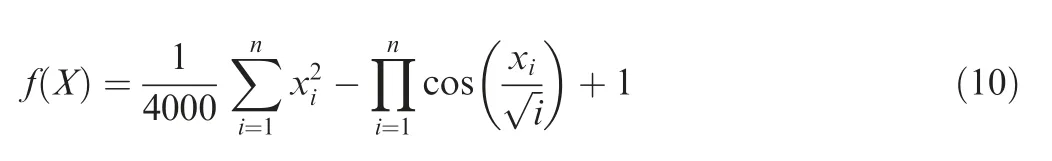
Fig. 9 shows the spatial surface of Griewank function, and it has a global minimum of 0. Fig. 10 shows the results of fitness varying with iterations via LHS-PSO algorithm,LHS-FDR-PSO algorithm and LHS-FDR-SOPSO algorithm.For all the three algorithms, original particles are distributed by LHS method, and the number of particles for each algorithm is set to be 50. It is obvious that LHS-FDRSOPSO algorithm has the fastest convergence rate in searching the global minimum.

Therefore,from the test results of Griewank function,it can be observed that, the convergence rate and global searching ability are improved obviously by adopting LHS-FDRSOPSO algorithm.

where F1, F2, ..., Fpare called the principal components of original data. As can be seen, the dimension of the transformed dataset is p, which is lower than the dimension of the original dataset namely m. Thus the design number is reduced from m to p. For a set of reduced design variables [v1, v2, ...,vp], it can be returned to the original design variables [u1, u2,..., um] through

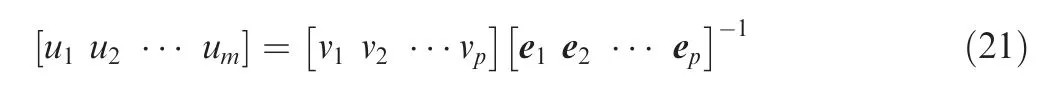
4.2. Establishment and training of DBN

DBN32is a type of deep learning network and is adopted in this study.Fig.11 shows the structure of DBN,and it is a type of multi-layer neural network consisting of one input layer, n hidden layers and one output layer. In this study, the input layer of the DBN represents the reduced design variables obtained via PCA, while the output layer of the DBN represents the aerodynamic parameters.

Distinguishing from conventional multi-layer neural networks,DBN employs a series of Restricted Boltzmann Machines (RBMs). The training of DBN is divided into two procedures.Firstly,a series of RBMs are trained layer by layer forward through unsupervised learning to preliminarily construct the DBN, and this procedure is also called pretraining of the DBN.Secondly,a Back Propagation(BP)neural network is established between the last two layers of the DBN to tune the weights of entire network backward in a supervised manner,and this procedure is also called fine tuning of the DBN.

Fig.12 shows the structure of a single RBM,and it consists of a visible layer and a hidden layer,which are connected bidirectionally. wij(i=1, 2, ..., m; j=1, 2, ..., n) is the weight associated with the connection between the hidden unit hjand the visible unit vi, biis the bias weight of the visible unit vi, and cjis the bias weight of the hidden unit hj.

The k-step contrastive divergence algorithm33incorporating Gibbs sampling method34is employed to train the RBM.By using this algorithm,estimations for all the weights are able to be obtained in k iterations.

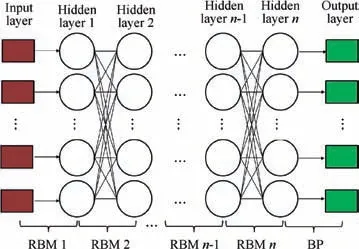
Fig. 11 Structure of DBN.

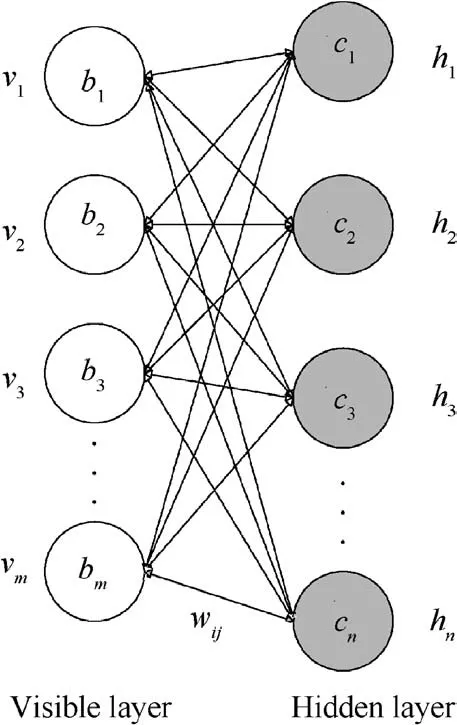
Fig. 12 Structure of a single RBM.

The original sample values are assigned to the visible layer of the first RBM, and the hidden layer of the first RBM is taken as the visible layer of the second RBM. And so on,the hidden layer of the previous RBM is taken as the visible layer of the next RBM. The purpose of training the RBMs is to obtain initial values of the entire network, and then all the weights of the network are tuned backward by the BP network in a supervised manner. By employing RBMs, DBN overcomes the shortcomings that BP network traps into local optimum easily and costs long training time caused by initializing the network randomly.

4.3. Validation of PCA-DBN-based surrogate model

In order to validate the accuracy of the PCA-DBN-based surrogate model, predictions for lift-to-drag ratios are conducted to a set of airfoils via BP-based surrogate model, Kriging surrogate model, DBN-based surrogate model and PCA-DBNbased surrogate model, and the prediction results are compared among these surrogate models.

Firstly, a database containing 30 airfoils is established via LHS method for training surrogate models. All the airfoils are parameterized with the six-order CST method,35and thus the number of variables for each airfoil is 14.Lift-to-drag ratio(L/D) of each airfoil is obtained through CFD simulations,and the computational conditions are set as: α=0°,Ma=0.7, Re=3×106. Next, PCA is implemented to the database to reduce the number of variables. Fig. 13 shows the contribution rates of principal components.As can be seen,the cumulative contribution rate of the first eight components reaches 95.57%, and thus the number of variables is reduced from 14 to 8.Then, a test group containing 5 airfoils is generated, and CFD simulations are performed to the 5 airfoils under the same computational conditions.Finally,predictions for lift-to-drag ratios are conducted to the 5 airfoils via different surrogate models.

Fig.14 shows the prediction results of lift-to-drag ratios for the 5 airfoils via different surrogate models compared with CFD results. As can be observed, the predictions by PCADBN-based surrogate model are closest to the results by CFD simulations.

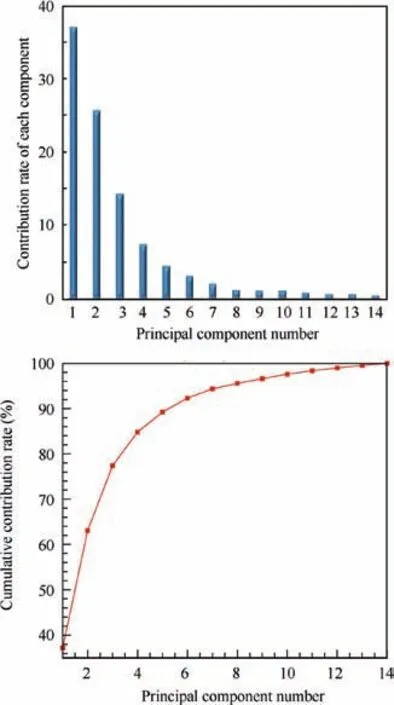
Fig. 13 Contribution rates of principal components for validation database.

Table 3 shows the average errors between predictions by different surrogate models and CFD results. Average error of PCA-DBN-based surrogate model is the smallest, which is only 3.11%.BP-based surrogate model has the largest average error of 5.91%.Average error of DBN-based surrogate model is slightly smaller than that of Kriging surrogate model.Therefore, from the comparison results of average errors, the PCADBN-based surrogate model established in this study obtains more accurate predictions than the other three surrogate models. Such results demonstrate that the PCA-DBN-based surrogate model is highly reliable, and it lays the foundation of aerodynamic optimizations.

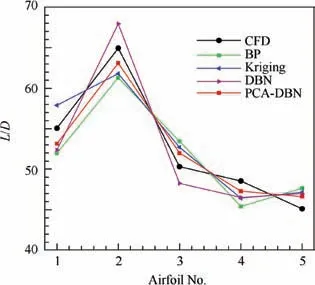
Fig. 14 Prediction results of lift-to-drag ratios via different surrogate models compared with CFD results.

5. Applications of PCA-DBN-based surrogate model

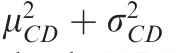
5.1. Robust optimization for NLF airfoil

NLF technology is an effective way to reduce drag for aircraft,and has attracted great attentions because it does not need any additional control mechanism or energy consumption compared to Laminar Flow Control (LFC) or Hybrid Laminar Flow Control (HLFC) technologies. Rashad and Zingg36achieved ASO for NLF airfoil using a discrete-adjoint approach, and obtained great drag reduction effect. Han et al.37conducted ASO of NLF wing using SBO approach,and achieved significant drag reduction.Their results indicated that SBO is feasible and effective for ASO of transonic NLF wings.

In this study, NLF (1)-0115 airfoil is selected as the original airfoil for the robust optimization under uncertainty of Mach number. The cruise conditions of NLF (1)-0115 airfoil are: Ma=0.65, CL=0.65, Re=3×106, and thus the range of Mach number for the robust optimization is set as[0.60, 0.70].

In order to build and train the PCA-DBN-based surrogate model for the NLF airfoil robust optimization, a database composed of 100 airfoils with both geometric parameters and aerodynamic parameters is generated via LHS method and CFD simulations. Each airfoil in the database is parameterized with the six-order CST method, and thus the original number of design variables is 14. Aerodynamic parameters are obtained by CFD simulations.For the robust optimization in the Mach number range of[0.60,0.70],aerodynamic parameters are mean drag coefficient CDmean, variance of drag coefficient Variancecd(Variancecd=, where σCDis the standard deviation of the drag coefficient), mean transition location on upper surface Xtrupmeanand mean transition location on lower surface Xtrlomean, respectively.

For the purpose of reducing the number of design variables,PCA is implemented to the geometric parameters of the airfoils in the database.Fig.15 shows the contribution rates of all the 14 principal components.As can be observed,the contribution rates of the first six components are 48.47%, 21.24%, 9.77%,7.10%, 5.74% and 2.79%, respectively, and the cumulative contribution rate of these six components reaches 95.09%.Therefore, the first six principal components are selected asthe new design variables, and thus the number of design variables is reduced from 14 to 6.

Table 3 Average errors between predictions by different surrogate models and CFD results.

After the new design variables are obtained, the DBN model is established and trained. The network consists of one input layer, 11 hidden layers, and one output layer. The input layer contains 6 units which represent the 6 design variables, the output layer contains 4 units which represent the 4 aerodynamic parameters, and each hidden layer contains 6 units. In this study, exponential linear unit described in Eq.(22) is selected as the activation function.

The well trained PCA-DBN-based surrogate model is then embedded in the improved PSO framework to predict aerodynamic parameters. For the robust optimization of NLF airfoil under uncertainty of Mach number, the optimization problem via the improved PSO framework can be described as follows:

Fig. 15 Contribution rates of principal components for NLF airfoil robust optimization.

The number of particles is 30,and the maximum iteration is 50. The NLF(1)-0115 airfoil is treated as an original particle for the improved PSO algorithm,and the convergent condition is satisfied at the 18th iteration as shown in Fig. 16. Fig. 17 shows the geometry of the optimized airfoil obtained via the robust optimization compared with the geometry of the original airfoil. After obtaining the optimized airfoil, CFD simulations are conducted to verify its aerodynamic characteristics in the Mach number range of[0.60,0.70],and aerodynamic characteristics of the optimized airfoil are compared with those of the original airfoil obtained by CFD simulations.

Table 4 shows comparison of aerodynamic parameters between the PCA-DBN-based surrogate predictions and the CFD results. As can be seen, the error of Variancecdreaches 10.58%, which is much larger than the other three errors.The reason for such a large error is that the fluctuation range of Variancecdis much larger than that of other aerodynamic parameters.However,because Variancecdis much smaller than, such an error of 10.58% contributes very little to the fitness function, and it can be deemed as acceptable. Besides the error of Variancecd, the errors of the other three aerodynamic parameters are all less than 3%, so it can be assumed that the PCA-DBN-based surrogate model serves very well during the optimization process.

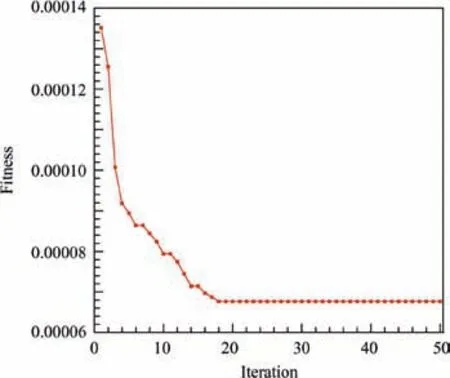
Fig.16 Convergence history of robust optimization for NLF(1)-0115 airfoil.

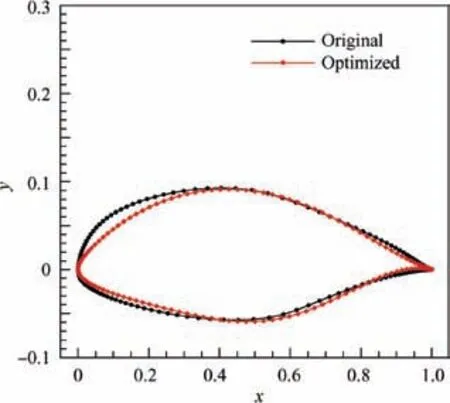
Fig. 17 Geometry comparison of airfoils.

Fig. 18 shows the skin friction coefficients on both upper and lower surfaces of the optimized airfoil compared with those of the original airfoil under the cruise conditions. The position where skin friction coefficient increases dramatically is viewed as the transition location.On upper surface,the transition location of the original airfoil is 49.97% of the chord length, while that of the optimized airfoil is 56.21% of the chord length.On lower surface,transition location of the original airfoil is 59.36% of the chord length, while that of the optimized airfoil is 61.25% of the chord length. Therefore,compared with the original airfoil, laminar flow length of the optimized airfoil is extended under the cruise conditions.

Fig. 19 shows the transition locations on both upper and lower surfaces of the optimized airfoil compared with those of the original airfoil in the Mach number range of [0.60,0.70].As can be seen,on either upper surface or lower surface,compared to the original airfoil, transition locations of the optimized airfoil are all moved backward in the Mach number range of [0.60, 0.70]. Therefore, compared with the original airfoil, laminar flow lengths of the optimized airfoil are extended dramatically in the Mach number range of [0.60,0.70].

Fig. 20 shows the drag coefficients of the optimized airfoil compared with those of the original airfoil in the Mach number range of [0.60, 0.70]. As can be observed, the drag coefficients of the optimized airfoil are all lower than those of the original airfoil in the Mach number range of [0.60, 0.70].Moreover, as Mach number increases, the variation gradient of drag coefficient of the optimized airfoil is smaller than that of the original airfoil as well.

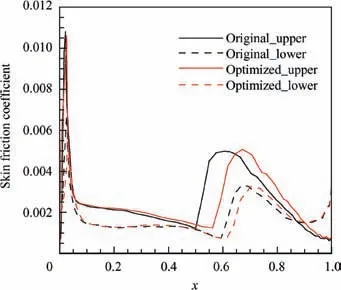
Fig. 18 Skin friction coefficient comparison under cruise conditions.

Fig.19 Transition locations comparison in Mach number range of [0.60, 0.70].

To sum up the above results, the PCA-DBN-based surrogate model works very well in the improved PSO framework for the robust optimization of NLF airfoil under uncertainty of Mach number, and the CFD results indicate that the optimized airfoil has much better aerodynamic characteristics than the original airfoil in the Mach number range of [0.60, 0.70].

Table 4 Comparison of aerodynamic parameters between PCA-DBN-based surrogate predictions and CFD results.

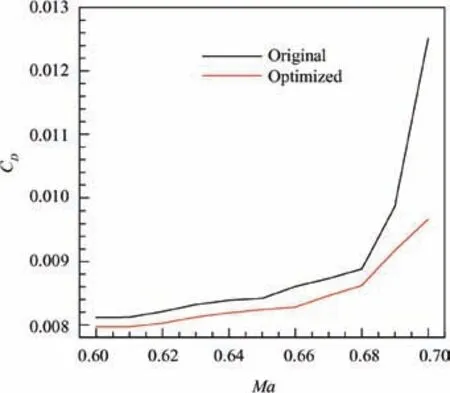
Fig. 20 Drag coefficients comparison in Mach number range of[0.60, 0.70].

5.2. Robust optimization for transonic wing

As shown in Fig. 21, the initial wing is installed on a wingbody model, and the geometric shape of the body remains unchanged during wing optimization process. Semi span of the wing is 17.204 m,leading sweepback angle is 27.4217°,root chord is 6.18 m, and tip chord is 1.518 m. Three control profiles are positioned at the root, the kink and the tip, respectively, the six-order CST method is employed to parameterize each control profile, and thus the number of design variables for each control profile is 14. Besides the CST variables of the three control profiles, the twist angles of three control profiles are also deemed as design variables.Thus, the initial number of design variables reaches 45.The cruise conditions of the wing-body are: Ma=0.785,CLwingbody=0.575, Re=2.3×107, and the range of Mach number for the robust optimization is set as [0.765, 0.805].

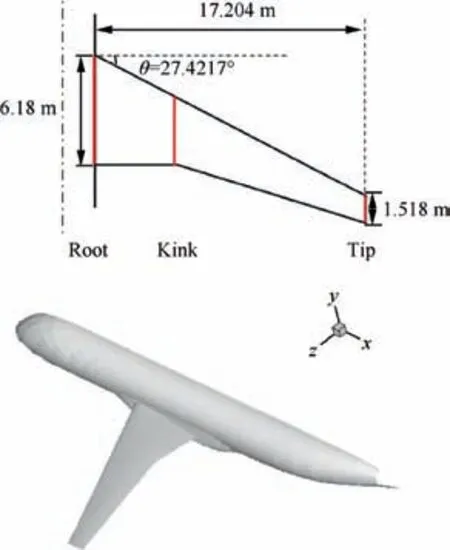
Fig. 21 Platform of wing and schematic of wing-body model.

In order to build and train the PCA-DBN-based surrogate model for the transonic wing robust optimization, a database composed of 130 wing-body configurations with both geometric parameters and aerodynamic parameters is generated via LHS method and CFD simulations. Geometric parameters include the CST parameters and the twist angle at each control profile, while aerodynamic parameters are obtained by CFD simulations.For the robust optimization of the transonic wing in the Mach number range of [0.765, 0.805], aerodynamic parameters are the drag coefficients at five different Mach numbers, namely CDMa=0.765, CDMa=0.775, CDMa=0.785,CDMa=0.795 and CDMa=0.805, respectively.

For the purpose of reducing the number of design variables,PCA is implemented to the geometric parameters of each control profile of the wing-body configurations in the database.Fig.22 shows the contribution rates of the 14 principal components at each control profile. As can be observed, the cumulative contribution rates of the first six components at the three control profiles are 95.31%,95.69%and 95.87%,respectively.Therefore, the first six principal components at each control profile are selected as the new design variables, thus the number of design variables for each control profile is reduced from 14 to 6, ant the total number of design variables is reduced from 45 to 21.

Based on the new design variables and aerodynamic parameters of the wing-body configurations in the database, the DBN model is established and trained. The network consists of one input layer, 18 hidden layers, and one output layer.The input layer contains 21 units which represent the 21 design variables,the output layer contains 5 units which represent the drag coefficients at the five different Mach numbers, and each hidden layer contains 21 units.Similarly,the exponential linear unit described in Eq.(22)is selected as the activation function.

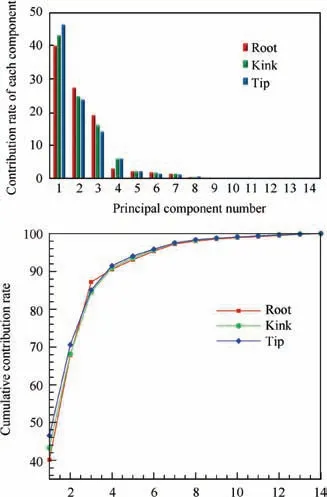
Fig. 22 Contribution rates of principal components for transonic wing robust optimization.

The robust optimization of transonic wing is performed via the improved PSO framework with the well trained PCADBN-based surrogate model. The optimization problem can be expressed as follows:

where μCDis the expectation of drag coefficient in the Mach number range of[0.765,0.805], and σCDis the standard deviation of drag coefficient in the Mach number range of [0.765,0.805].

The number of particles is 20,and the maximum iteration is 50.The initial wing-body configuration is treated as an original particle for the improved PSO algorithm,and the optimization is converged at the 23rd iteration as shown in Fig. 23. Fig. 24 shows the geometric shape of the optimized wing and the comparison of the three control profiles between the initial wing and the optimized wing. After obtaining the geometry of the optimized wing, CFD simulations are conducted to verify the aerodynamic performance of the wing-body configuration in the Mach number range of [0.765, 0.805].

Fig. 25 shows the comparison of sectional pressure coefficients of the initial wing and the optimized wing at different spanwise locations by CFD simulations under cruise conditions.As can be seen,the shock waves of the optimized configuration are weakened compared to the initial configuration,which makes a contribution to the drag reduction.

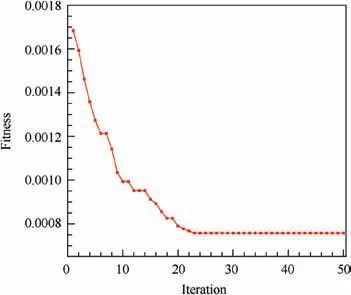
Fig. 23 Convergence history of robust optimization for transonic wing.

Fig. 24 Geometric shape of optimized wing and comparison of three control profiles.

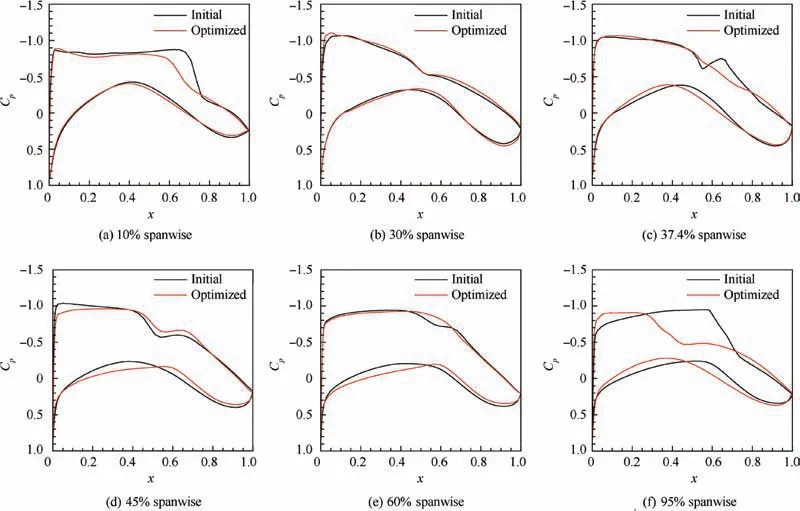
Fig. 25 Comparison of sectional pressure coefficients at different spanwise locations.

Fig. 26 Comparison of drag coefficients for transonic wing robust optimization.

Fig. 26 shows the comparison of drag coefficients among the CFD results of the initial wing,the CFD results of the optimized wing, and PCA-DBN-based surrogate predictions for the optimized wing. As can be seen, the drag coefficients of the optimized wing are much lower than those of the initial wing in the Mach number range of[0.765,0.805],and the gradient of the drag coefficient is decreased greatly by the robust optimization.The drag coefficients by PCA-DBN-based surrogate model are all slightly greater than those by CFD simulations for the optimized wing. The reason for such differences between surrogate predictions and CFD results is the tradeoff between the training cost and the accuracy of the surrogate model. In order to reduce the training cost of the surrogate model, limited training samples are used and thus the prediction accuracy is influenced.In addition,the variation tendency of the surrogate prediction in the Mach number range of[0.765, 0.805] is basically in accordance with that of the CFD result.

To be more specific, Table 5 shows the errors between the PCA-DBN-based surrogate predictions and CFD results.The errors of the drag coefficients at five different Mach numbers are all less than 3%, and the largest one is only 2.67%.

Given the above results, the PCA-DBN-based surrogate model serves very well as a prediction model in the robust optimization process of the transonic wing.Compared to the initial wing, the drag coefficients of the optimized wing are reduced greatly by the robust optimization. By employing thePCA-DBN-based surrogate model,the computational amount is reduced a lot, and thus the optimization efficiency is improved obviously.

Table 5 Errors between PCA-DBN-based surrogate predictions and CFD results.

6. Conclusions

In this study, an efficient optimization method employing a PCA-DBN-based surrogate model is developed and then applied to the robust aerodynamic design optimizations of NLF airfoil and transonic wing.

The six-order CST method is used to parameterize the airfoil and control profiles of the wing. The PCA technique is implemented to the CST parameters in order to reduce the number of design variables.After obtaining the reduced design variables, the DBN model is established with the reduced design variables as input and the aerodynamic parameters as output.The DBN model is trained using the k-step contrastive divergence algorithm. The PCA-DBN-based surrogate model is validated via predicting lift-to-drag ratios of 5 airfoils in a test group, and the results indicate that the PCA-DBN-based surrogate model has a strong competence and obtains more accurate predictions than BP-based surrogate model, Kriging surrogate model and DBN-based surrogate model.

For the purpose of improving the convergence rate and global searching ability, an improved PSO algorithm is proposed with several improvements implemented to the standard PSO algorithm. LHS method is conducted to distribute original positions of the particles, and a second-order oscillating scheme along with an FDR item are used to update velocities and positions of the particles. The test results for Griewank function indicate an obvious increment of convergence rate by the improved PSO algorithm. Then the PCA-DBN-based surrogate model is embedded in the improved PSO framework to predict aerodynamic parameters in the optimization processes.

The robust optimizations of NLF airfoil and transonic wing are performed via the improved PSO framework with the PCA-DBN-based surrogate model. The number of design variables is reduced from 14 to 6 for the robust optimization of NLF airfoil,while the number of design variables is reduced from 45 to 21 for the robust optimization of transonic wing.The results indicate that the prediction values by the PCADBN-based surrogate model are close to CFD results for both two robust optimizations.The developed efficient optimization method serves very well in the optimization processes, and improves the optimization efficiency obviously.

Acknowledgments

This study was co-supported by Aeronautical Science Foundation of China (No. 2015ZBP9002) and China Scholarship Council.