Hybrid integration method for highly maneuvering radar target detection based on a Markov motion model
Yingxio ZHAO, Zengping CHEN, Yue ZHANG,*, Jie CHEN,Jiong YANG, Yunsheng XIONG
a National Key Laboratory of Science and Technology on ATR,National University of Defense Technology,Changsha 410073,China
b School of Electronic and Communication Engineering, Sun Yat-sen University, Shenzhen 518107, China
KEYWORDS Binary integration;Dynamic programming;Long-time integration;Maneuvering targets;Markov motion model;Radar target detection;Radon-Fourier transform
Abstract To detect highly maneuvering radar targets in low signal-to-noise ratio conditions, a hybrid long-time integration method is proposed, which combines Radon-Fourier Transform(RFT),Dynamic Programming(DP),and Binary Integration(BI),named RFT-DP-BI.A Markov model with unified range-velocity quantification is formulated to describe the maneuvering target’s motion.Based on this model,long-time hybrid integration is performed.Firstly,the whole integration time is divided into multiple time segments and coherent integration is performed in each segment via RFT.Secondly,non-coherent integration is performed in all segments via DP.Thirdly,2/4 binary integration is performed to further improve the detection performance.Finally,the detection results are exported together with target range and velocity trajectories. The proposed method can perform the long-time integration of highly maneuvering targets with arbitrary forms of motion.Additionally, it has a low computational cost that is linear to the integration time. Both simulated and real radar data demonstrate that it offers good detection and estimation performances.
1. Introduction
With the development of aerial technology, many types of weak, high-speed, and highly maneuvering targets have been developed, which are difficult for radars to detect.1,2RacerX,the fastest electric Unmanned Aerial Vehicle (UAV) known,can fly at a maximum speed of 0.22 Ma with a weight of only 0.8 kg.3Dark Sword, a stealth UAV from China, can fly at a speed of 1 Ma.4Released from the pilot’s physiological limits,its maneuvering accelerations can easily exceed 10 g.Pioneer,a new missile developed by Russia, can fly at a speed of 20 Ma with a maneuvering acceleration of 100 g.5
Long-time integration is an effective method for improving the Signal-to-Noise Ratio (SNR) to enable maneuvering weak radar target detection. The two main types of long-time integration are coherent integration and non-coherent integration.
In coherent integration methods, both the amplitude and phase information of echo waves are used. Moving Target Detection (MTD)6is a basic method of coherent integration via Doppler filter banks. However, for maneuvering targets,Across Range Unit (ARU) effects and Doppler Frequency Migration (DFM) can easily occur among the echo waves of the moving target, and thus range and phase compensation should be implemented respectively.
To perform range compensation when using coherent integration, the methods mainly used are the Keystone7,8,Radon9-11, SCaled Inverse Fourier Transform (SCIFT)12,Frequency-Domain Deramp-Keystone Transform(FDDKT)13, generalized Keystone14, generalized Radon15-18,and Adjacent Cross Correlation Function(ACCF)19methods.The Keystone, Radon, SCIFT, and FDDKT methods are applied in one-order range migration.The generalized Keystone and generalized Radon methods are applied in high-order range migration.The ACCF method is for arbitrary forms of motion but yields poor performance at low SNR conditions.
To perform phase compensation when using coherent integration, the methods mainly used are the Fourier Transfrom(FT)6,10,de-chirp20,FRactional Fourier Transform(FRFT)16,LV’s Distribution(LVD)17,chirp-let21,Dicrecte Chirp Fourier Transform (DCFT)22, FRactional Ambiguity Function(FRAF)18, generalized de-chirp14, and Polynomial-Phase Signal(PPS)23,24methods.The FT method is for one-order phase changes.The de-chirp,FRFT,LVD,and chirp-let methods are for two-order phase changes. The FRAF method is for threeorder phase changes. The generalized de-chirp and PPS methods are for high-order phase changes.
Most coherent integration algorithms compensate for range walk and phase modulation respectively in sequence, such as the Keystone-dechirp20, Radon-FRFT16, Radon-LVD17,Radon-FRAF18,ACCF-LVD19,and General Keystone Transform and General De-chirp (GKTGDP)14algorithms. Based on the coupling relationship between range walk and phase changes, Xu et al.10proposed in 2011 the Radon Fourier Transform (RFT) and Generalized Radon Fourier Transform(GRFT)algorithms.They can compensate for range migration and phase changes simultaneously.
In non-coherent integration methods, only the amplitude information of echo waves is used. The main non-coherent integration methods are the Hough transform25, maximum likelihood26, dynamic programming27-30, recursive Bayesianbased31,32, and random finite sets-based33-35methods. For the Hough transform and maximum likelihood methods,actual target movement must correspond to the built motion model. For the recursive Bayesian-based and random finite sets-based methods, additional target maneuverability can be allowed by adding a random variable to the target motion model. In general, they are realized using particle filtering,which may not cover all possible target motions.The Dynamic Programming (DP) approach, given the scope of the target state transition, is equivalent to performing an exhaustive search but has a much lower computational cost. Moreover,specific forms of motion, such as one-order or two-order motion need not be assumed. Thus, DP is a more suitable method for highly maneuvering targets.
However, problems still exist in current research. Firstly,when using coherent integration methods, longer integration times result in higher Doppler resolution, which sharply increases computational costs and worsen the tolerance to target maneuvering. An excessively long coherent integration time even leads to the inner-target Doppler resolution effect,according to the theory of Inverse Synthetic Aperture Radar(ISAR)36,37, which causes the target energy to disperse in multiple resolution units. Secondly, when using noncoherent integration methods, they exhibit poor performance and may even become invalid at low SNR conditions.Thirdly, most of the above-mentioned methods are based on polynomial target motion models.38As the integration time increases, more orders are needed to describe the motion of highly maneuvering targets, which leads to huge computational cost. Additionally, polynomial models are not appropriate when the acceleration or jitter suddenly change, such as during the ignition of an engine, when a plane is affected by rapid airflows, or in the precise moment when a baseball is hit. Although some papers tried to solve the three abovementioned problems, the effectiveness may be not satisfactory in some circumstances. In Refs.39-43, hybrid integration is adopted which combine inner-segment coherent integration and across-segment non-coherent integration to make a balance of performance and computation cost. However, those methods use polynomial target motion model, which can’t solve the third problem. In Ref.44, dynamic programming is introduced to coherent integration, which can fit arbitrary maneuvering target motion with a low computation cost.However, its simple Markov target motion model may bring too much extra noise which deteriorates the integration performance, and it can’t fit multi-target scene with intersecting trajectories.
To deal with the three above-mentioned problems, this paper proposes a hybrid integration algorithm called RFTDP-BI. A Markov target motion model with united range and velocity quantification is built to describe arbitrary forms of maneuvering target motion. Based on the model, coherent RFT is made in each time segment, non-coherent DP is made across all segments,and 2/4 binary integration is made via window shift of the whole integration time. Under this model,RFT acquires the maximum time length of valid integration,and DP has much less false alarms than traditional DPbased algorithms with the redundant state series cleared.RFT-DP-BI shows good detection and estimation performance for highly maneuvering targets with low computational cost.The rest of this paper is organized as follows.In Section 2,the system model and integration problem are formulated. In Section 3, the hybrid integration method is proposed. In Section 4, the computational cost is analyzed. In Section 5,numerical experiments are provided.In Section 6,experiments with raw radar data are conducted. In Section 7, conclusions are given.
2. System model and problem formulation
In this section, the signal model and the maneuvering target motion model are built,and the long-time integration problem is formulated.


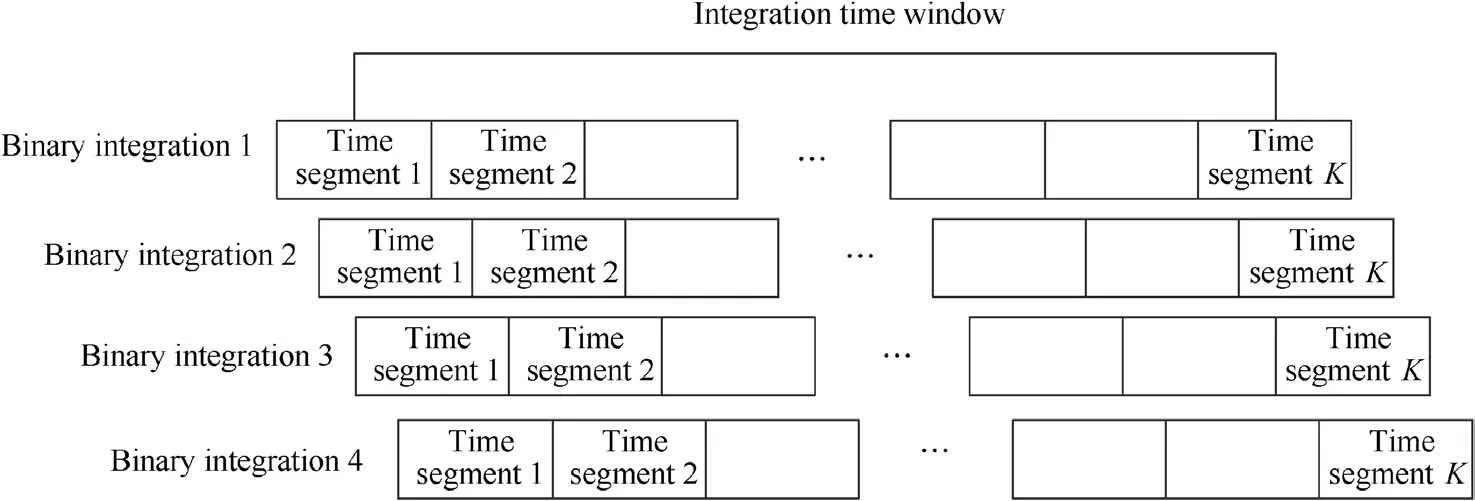
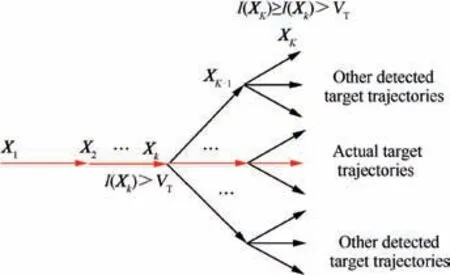
Fig. 2 Window shift of 2/4 binary integration detection.
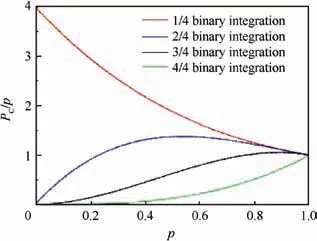
Fig. 3 Curves of PC/p in binary integration.
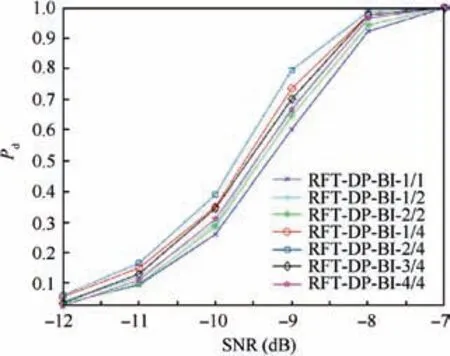
Performance of RFT-DP-BI with different binary integration principles will be further compared through numerical results in Section 5,which verifies the superiority of 2/4 binary integration.
3.4. Acquirement of target trajectories via DP backtracking
Next, the target trajectories ^X1: ^XKwill be attained through DP backtracking.To fit binary integration and filter extraordinary trajectories, some adjustments to traditional DP backtracking procedure is made in this study.
Find all detected states ^XKafter 2/4 binary integration,i.e.:
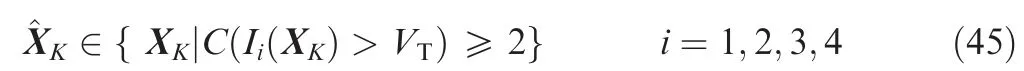
For each ^XKin Eq. (45), the group number l of DP results should be identified, which has maximum Ii(^XK), i.e.:

Then the correspondent target trajectory ^X1: ^XKis attained in the l - th DP results group,where traditional DP backtracking is applied27, i.e.:
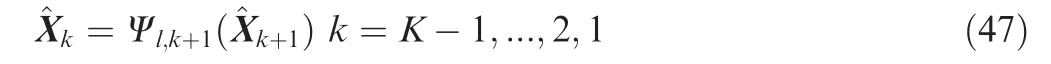
where Ψl,k()denotes the DP backtracking index function Ψk()of Eq. (41) in the l - th DP results group.
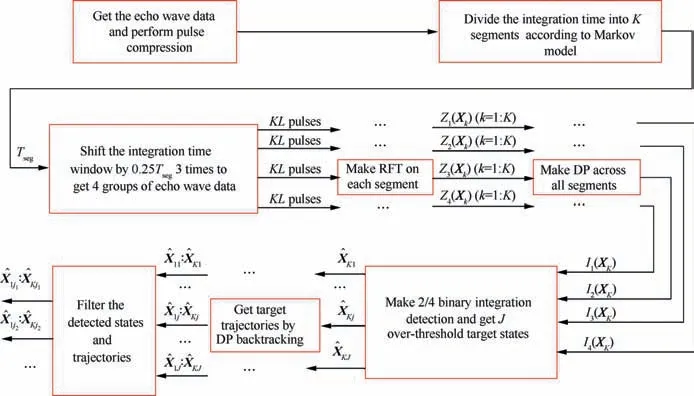
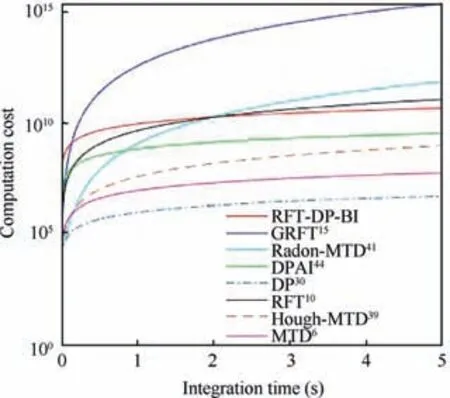
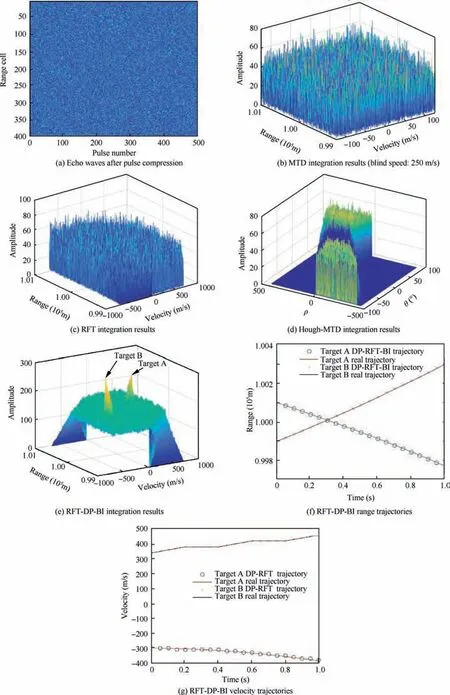
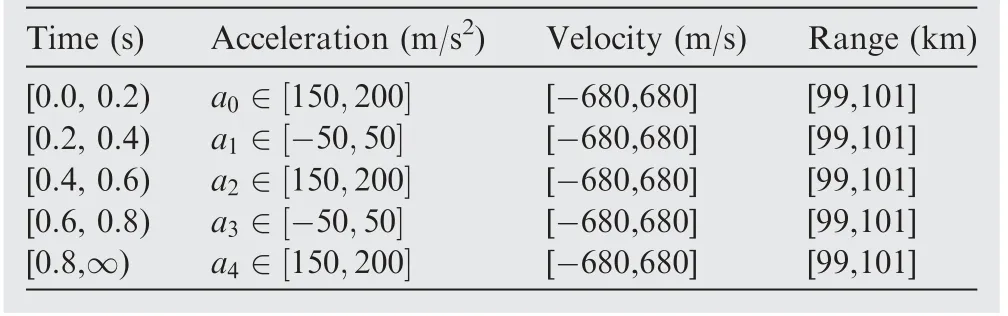
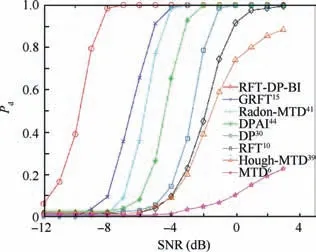
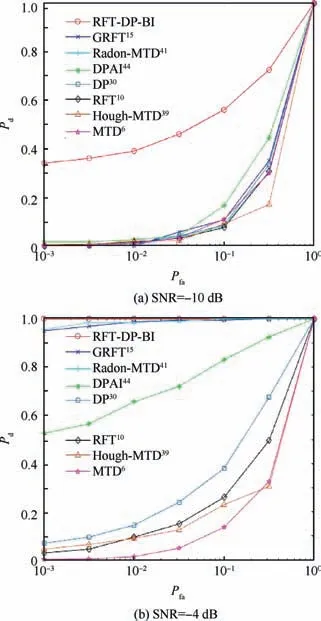
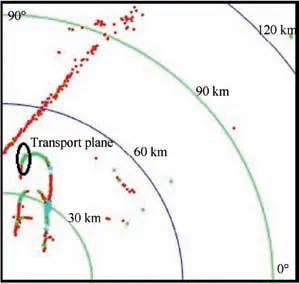
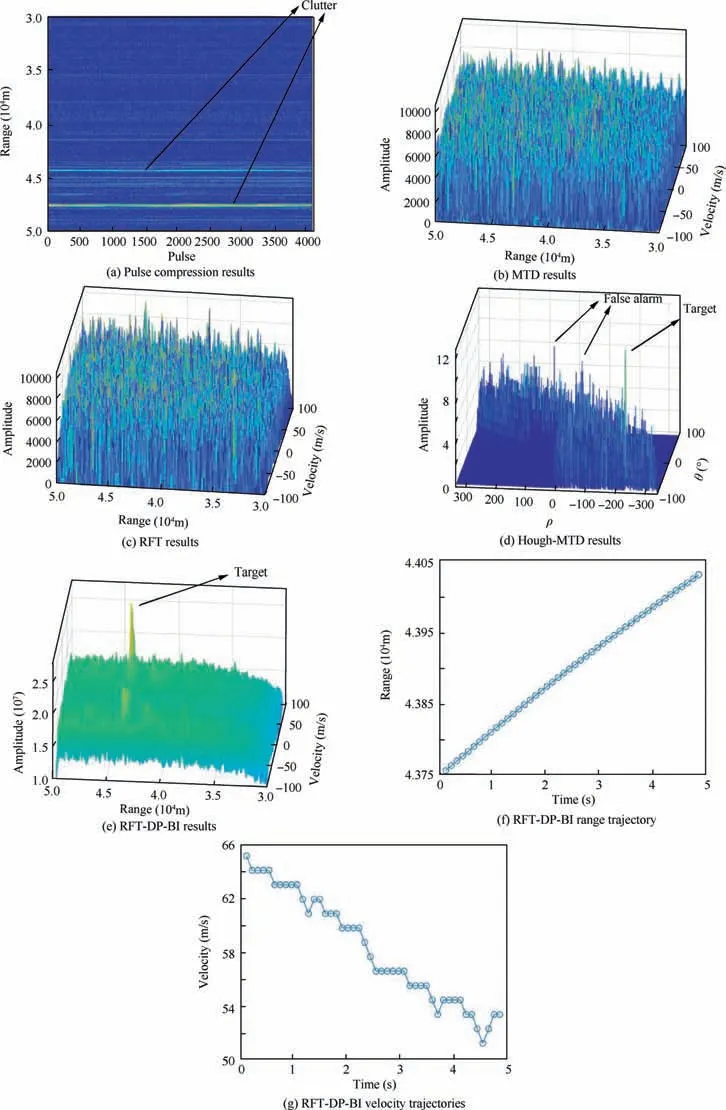
After DP backtracking, multiple trajectories with a common state node may be attained,which are from the same target. According to Eq. (40), if I(Xk)>VT,k The extraordinary states and trajectories will increase false alarms and bring huge pressure to subsequent signal processing. Thus, they should be further filtered. Some restrictions are constructed in the proposed algorithm. ^XKshould be the locally maximum point, and trajectories with W common states ^X1: ^XWshould be cleaned, i.e.: where Xk(XK) denotes the state Xkwhich is backtracked from XK. In this study,parameters D1,D2,W are set up as Eqs.(50)-(52).Their values can be adjusted in actual application according to target characteristics. In Sections 3.1-3.4, a hybrid integration method RFT-DP-BI was proposed. The complete procedure is summarized as follows, with the flowchart shown in Fig. 5. Step 1. get the echo wave data and perform pulse compression. Fig. 4 Recovered trajectories from the same target. Fig. 5 Flowchart of RFT-DP-BI. Step 2.the integration time is divided into K time segments.The time segment length Tsegis calculated according to Eq. (23). Step 3. the integration time window is shifted by 0.25Tsegsubsequently, acquiring 4 groups of pulse compression data.For each group of data, Steps 4 and 5 are carried out. Step 4.RFT results Z(Xk)is attained in each time segment according to Eqs. (30)-(32). Step 5. using Z(Xk) (k=1,2,...,K), DP results I(XK) is attained, according to Eqs. (38)-(41). Step 6. using 4 groups of Ii(XK) (i=1,2,3,4), the detected states ^XKare attained via 2/4 binary integration,according to Eq. (45). Step 7.for each detected state ^XK,the correspondent target trajectory ^X1;^XKis attained through DP backtracking according to Eqs. (46) and (47). Step 8.the detected states and trajectories of targets are further filtered according to Eqs. (48) and (49). According to Eq. (30), Eqs. (40), and (43), which is the main computation in RFT, DP and BI respectively, the main computational cost of RFT-DP-BI is where M is the total pulse number,NRand NVare the number of range and velocity units, respectively, K is the number of time segments, ICAand IRArepresent complex and real addition, respectively, ICMstands for complex multiplication, and Imax3is the maximum operation among three real numbers. Replacing parameters M, NR, NV, and K with n, the computational cost is O(n3), which is in the equal level to that of RFT. Let rwdenote the range search scope,vwdenote the velocity search scope and Tintdenote the integration time, the computational cost of RFT-DP-BI in Eq.(53)can be further derived as To make a comparison on computation cost,several typical integration methods were selected, including coherent methods, namely MTD6, RFT10, two-order GRFT15, and DPAI44,a non-coherent method, namely DP30, and hybrid integration methods, namely Hough-MTD39, three-order Radon-MTD.41For Ts=20 ns, Tr=200 ms, λ=1 m,amax=100 m/s2, rw=2 km, and vw=340 m/s2, a plot of the computational cost versus the integration time is shown in Fig. 6. Fig. 6 Computational cost of eight integration methods versus integration time. From Fig.6,the computation cost of RFT-DP-BI makes a slower growth with than RFT, Radon-MTD, and GRFT.Their computation cost is linear toandrespectively. The polynomial motion model, which used in the above 3 Radon-based algorithms, requires smaller resolution unit of motion parameters for longer integration time,which will bring extra orders of Tintin the expression of computation cost. Thus, the polynomial motion model is not suitable to make fast implementation in the scenario of highly maneuvering targets or long integration time. In contrast,using the Markov motion model, the computation cost of RFT-DP-BI is linear to Tintaccording to Eq. (54), which is easier to make fast implementation of long time integration.Although RFT-DP-BI has higher computation cost than DPAI, Hough-MTD, DP, and MTD, it has better performance in highly maneuvering target detection and estimation,which will be further discussed in Section 5. In this section,numerical simulations are presented to evaluate the performance of the RFT-DP-BI method. The parameters of the radar are shown in Table 1. Two maneuvering targets were simulated. Target A made accelerated motions and uniform motions alternately with a duration of 200 ms. It moved from 99.9 km with an initial velocity of 340 m/s2and an initial acceleration of 200 m/s2.Target B made three-order motions from 100.1 km with an initial velocity of -340 m/s, an initial acceleration of -10 m/s2,and a jitter of -180 m/s3. Their trajectories were intersected in the r-tmplane. Set the SNR after pulse compression as-5 dB.Integration results were acquired via RFT-DP-BI and several typical integration methods,including MTD,RFT,and Hough-MTD,as shown in Fig.7.From Fig.7(a),it can be seen that the targets were totally buried in the noise. Because of the complicated ARU and DFM effects,the typical coherent integration methods MTD and RFT became invalid,as shown in Fig.7(b)and Fig. 7(c). The results of the typical hybrid integration method Hough-MTD are shown in Fig. 7(d), where ρ and θ are the parameters in Hough transform. ρ denotes the distance from the origin to the trajectory line, and θ denotes the angle of the trajectory line’s normal vector. Hough-MTD also showed poor results, because low SNR after MTD makes the subsequent non-coherent integration invalid. In contrast, the RFT-DP-BI method yielded good integration results with a clear distinction between the noise and the targets, as shown in Fig. 7(e). In Fig. 7(f) and Fig. 7(g), it can be seen that the recovered range and velocity trajectories by RFT-DP-BI were consistent with the true trajectories. Several typical integration methods were selected to make a comparison with RFT-DP-BI on detection performance,including coherent methods, namely MTD6, RFT10, two-order GRFT15, and DPAI44, a non-coherent method, namely DP30, and hybrid integration methods, namely Hough-MTD39and three-order Radon-MTD.41To further verify the superiority of 2/4 binary integration which has been demonstrated in Section 3.3, different binary integration principles for RFT-DP-BI are also compared. For simplicity, only one target was used in the simulations. To simulate arbitrary maneuvering targets,the target’s motion parameters were random selected in each Monte Carlo trial, and the acceleration changed every 200 ms, as shown in Table 2. Gaussian noise was added to the target echoes.One thousand Monte Carlo trials were made for each SNR, ranging from -12 dB to 3 dB after pulse compression. Table 1 Parameters of radar. The curves of target detection probability Pdversus the SNR for different binary integration principles of RFT-DPBI are shown in Fig. 8, with the false alarm probability in the whole state space set as Pfa=10-2. In Fig. 8, RFT-DPBI-1/1 has the lowest Pdin each SNR, indicating that the detection performance is improved after binary integration.RFT-DP-BI-2/4 has the highest Pdin each SNR, indicating that 2/4 binary principle is an optimum selection for RFTDP-BI, which is consistent with the theoretical analysis in Section 3.3. The curves of target detection probability Pdversus the SNR for different integration algorithms are shown in Fig.9,with the false alarm probability in the whole state space set as Pfa=10-2.To make a more comprehensive comparison,the ROC curves for different integration algorithms are also plotted as shown in Fig. 10(a) and (b), with the SNR set as-10 dB and -4 dB, respectively. The simulation results in Figs.9 and 10 show that the RFTDP-BI algorithm acquires better detection performance than the others in the case of highly maneuvering target motion. MTD exhibited poor performance because of serious ARU and DFM effects. Hough-MTD showed better detection performance than MTD with the help of Hough transform to overcome ARU effects, but it became invalid in low SNR because low SNR after MTD can’t support subsequent noncoherent Hough transform. Radon-based algorithms (RFT,Radon-MTD, and GRFT) exhibited lower performance than RFT-DP-BI because the target acceleration undergoes sudden changes four times during the integration time,which is not fitted to the polynomial model used in these algorithms.Although the DP-based algorithm(DP and DPAI)can fit arbitrary forms of target motion, it shows poor detection performance at low SNR, because too simple restrictions are added to the target state transition, without considering the specified target maximum acceleration and the coupling relationship of the range and velocity. Consequently, many redundant state trajectories and extra false alarms are brought into the dynamic programming. By contrast, based on the proposed Markov target motion model, the RFT-DP-BI method has no redundant state trajectories, decreasing the false alarms of traditional DP-based methods. Moreover, RFT-DP-BI acquires the maximum time segment length for RFT according to the specified maximum target acceleration,which can make full use of the superiority of coherent integration. Thus, the proposed RFT-DP-BI algorithm shows a better detection performance for highly maneuvering weak targets. Fig. 7 Integration results for targets A and B. Table 2 Target motion parameters in Monte Carlo trials. Fig. 8 Detection probability of RFT-DP-BI with different binary integration strategies. Fig. 9 Detection probability of eight integration methods for different SNRs. Fig. 10 ROC curves of eight integration methods. Next,the performance of target state estimation was compared among the above-mentioned algorithms. They had different defined target state spaces with different motion parameters.To make a unified comparison, the Root Mean Square Error(RMSE) of the range and velocity values at tm=1 s was estimated for these algorithms. Maximum-likelihood estimation was applied to the integration results. For the DP algorithm,the target state space only comprises range information, and its velocity estimation is not performed. The RMSE results are shown in Fig. 11. From Fig.11(a)and(b),we can see that the RMSEs of the RFT-DP-BI method were lower than those of the other algorithms, and the former rapidly converge to zero as the SNR increases. The other methods yielded low estimation performances with unfit models for highly maneuvering motion. In Fig. 11(b), it can be seen that the velocity RMSE of the MTD and DPAI algorithms could not even converge to zero because of their low capability for overcoming velocity ambiguities. Fig.11 RMSE of eight integration methods for different SNRs. Fig. 12 The L-band staring array radar. Table 3 Parameters of the L-band staring array radar developed by NUDT-ATR laboratory. In this section, we use the raw radar data to verify the effectiveness of our proposed detection algorithm. The raw data were recorded using an L-band staring array radar developed by NUDT-ATR laboratory; it is shown in Fig.12.It has a low-power broad transmit beam and multiple receive beams. And long-time integration should be made before target detection. The parameters of the radar are listed in Table 3. With the L-band staring array radar, we carried out a field experiment near an airport. The echo waves from a transport plane about 40 km far away were received and analyzed,whose flight trajectory in the azimuth-range plane is shown in Fig. 13. When the transport plane making a turning flight, it had high maneuverability with the radial velocity decreased rapidly. The relevant data segment is acquired, comprising 4096 pulses in total. And the processing results are shown in Fig.14.In Fig.14(a),the target is buried in the noise and clutter and can’t be seen after pulse compression. So, long-time integration methods should be further implemented. The RFT-DP-BI is compared with several typical coherent or hybrid integration methods, including MTD, RFT, and Hough-MTD, which are commonly applied in engineering.The integration results are shown in Figs. 14(b)-(g). Fig. 13 Measured flight trajectory in azimuth-range plane. Fig. 14 Processing results of the echo waves. In Figs. 14(b) and (c), the typical coherent methods MTD and RFT even becomes invalid,because of low SNR and serious DFM and ARU effects caused by the turning flight. In Fig. 14(d), the hybrid integration method Hough-MTD acquires obviously better results than MTD and RFT, with the target observable after integration. Although the radial velocity of the transport plane changed rapidly in the turning flight, the range unit migration was approximately linear because of large range resolution unit of the experiment radar.Under this occasion, Hough transform is still valid and can further improve the SNR after MTD. However, after Hough-MTD, the noise still has strong fluctuation with the existence of some false alarms, because the maximum operation along the Doppler dimension after MTD and the threshold-crossing binary operation before Hough transform makes part of the target information lost, decreasing the integration effectiveness. In Fig. 14(e), RFT-DP-BI shows better integration performance than Hough-MTD, with a clear distinction between the noise and the targets. With the help of the proposed Markov target motion model, the RFT-DP-BI method can describe maneuvering target motion more flexibly and more accurately with smaller velocity and range quantification unit than the Hough-MTD method. The velocity and range trajectory attained by RFT-DP-BI after DP backtracking are shown in Figs. 14(f) and (g) respectively, which are basically consistent with the turning flight of the transport plane. In conclusion, the proposed algorithm RFT-DP-BI has been verified by the processing results of the real data,showing a good effectiveness of maneuvering target detection and estimation. In this paper, a hybrid integration method called RFT-DP-BI was proposed to detect weak maneuvering targets. A Markov target motion model with unified range and velocity quantification is built to describe maneuvering target motion, based on which coherent RFT, non-coherent DP, and 2/4 binary integration are applied to make hybrid integration. It offers the following advantages. (1) It supports arbitrary forms of target motion. Only the maximum acceleration,the velocity scope,and the range scope need to be set up. The number of target motion orders needn’t to be restricted and sudden changes of motion parameters (acceleration, jitter, etc.) are permitted. (2) It exports detection results with target range and velocity trajectories, integrating detection and tracking. (3) It has a low computational cost which is linear to the integration time. Results of both simulation and real data demonstrate its superiority over existing methods. This study was supported by the National Natural Science Foundation of China (No. 6157010118). And thanks for the engineers Cong CHEN, Yunfeng FU, Qiang SONG, Dingyi LIU, Yanshuang WANG of NUDT-ATR laboratory for developing and operating the L-band staring array radar.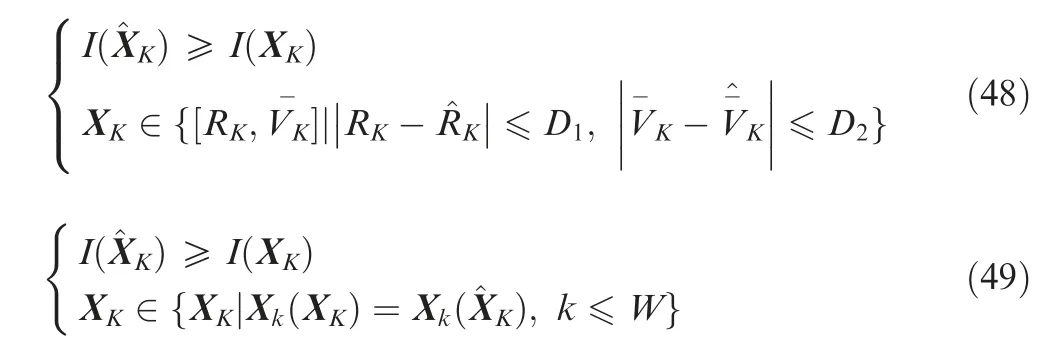

3.5. Complete procedure of RFT-DP-BI
4. Computational cost
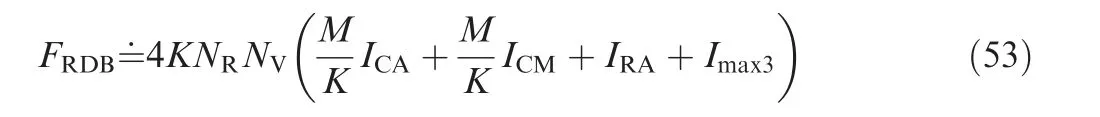
5. Numerical results
5.1. Integration results for maneuvering targets
5.2. Comparison of detection performance

5.3. Comparison of estimation performance


6. Experiment with raw radar data
7. Conclusions
Acknowledgements
 CHINESE JOURNAL OF AERONAUTICS2020年6期
CHINESE JOURNAL OF AERONAUTICS2020年6期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- A novel variable structure multi-model approach based on error-ambiguity decomposition
- Multi-block SSD based on small object detection for UAV railway scene surveillance
- A new online modelling method for aircraft engine state space model
- Cross-sectional deformation of H96 brass double-ridged rectangular tube in rotary draw bending process with diあerent yield criteria
- Application of a PCA-DBN-based surrogate model to robust aerodynamic design optimization
- Numerical exploration on the thermal invasion characteristics of two typical gap-cavity structures subjected to hypersonic airflow
