Model-free adaptive optimal design for trajectory tracking control of rocket-powered vehicle

Wenming NIE, Huifeng LI, Ran ZHANG,*

a School of Astronautics, Beihang University, Beijing 100083, China

b Key Laboratory of Spacecraft Design Optimization and Dynamic Simulation Technologies, Ministry of Education, Beijing 100083, China

KEYWORDS Adaptive dynamic programming;Dynamic neural network;Model-free;Solid-rocket-powered vehicle;Trajectory tracking

Abstract An adaptive optimal trajectory tracking controller is presented for the Solid-Rocket-Powered Vehicle (SRPV) with uncertain nonlinear non-affine dynamics in the framework of adaptive dynamic programming. First, considering that the ascent model of the SRPV is non-affine, a model-free Single Network Adaptive Critic (SNAC) method is developed based on the dynamic neural network and the traditional SNAC method.This developed model-free SNAC method overcomes the limitation of the traditional SNAC method that can only be applied to affine systems.Then,a closed-form adaptive optimal controller is designed for the non-affine dynamics of SRPVs.This controller can adjust its parameters under different flight conditions and converge to the approximate optimal controller through online self-learning. Finally, the convergence to the approximate optimal controller is proved.The theoretical analysis of the uniformly ultimate boundedness of the tracking error is also presented.Simulation results demonstrate the effectiveness of the proposed controller.

1. Introduction

* Corresponding author.

E-mail address: wenming0912@buaa.edu.cn (R. ZHANG).

Peer review under responsibility of Editorial Committee of CJA.

https://doi.org/10.1016/j.cja.2020.02.022 1000-9361 © 2020 Chinese Society of Aeronautics and Astronautics. Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

The endo-atmospheric trajectory tracking control of Rocket-Powered Vehicles (RPV) is troublesome due to convoluted nonlinear dynamics of the vehicle,significant aerodynamic disturbances and the stringent requirements for achieving higher tracking performance with limited available control capabilities. For missions involving RPV trajectory tracking control problems, good trajectory tracking performance is a prerequisite for mission success, such as Mars entry missions,1cruise missions of Air-breathing Hypersonic Vehicles (AHV),2orbiting missions of Launch Vehicles (LV)3and Reusable Launch Vehicles (RLV).4Thus, the trajectory tracking of RPVs has been well recognized as an important technology in aerospace engineering.

In the literature,many methods have been proposed for the tracking control of RPVs.The current methods can be mainly divided into two categories: the stable tracking controller based on nonlinear control theories1,4-10and the optimal tracking controller based on the optimal control theories.3,11,12In the first category, the trajectory linearization method, combined with gain scheduling method,has been widely adopted in the trajectory tracking control for RLVs.4,5Another most commonly used method is Nonlinear Dynamic Inversion(NDI).6It should be noted that the NDI method relies on an accurate system model. However, in practice, the exact model of a system is difficult to obtain.To solve this problem,the researchers improved NDI by subtly combining it with robust control theory,7radial basis function network,8and so on.Moreover,the adaptive control,2sliding mode control,9and active disturbance rejection control10are all applied to the trajectory tracking control of RPVs. In the second category,the optimal control theories are employed. Due to the complexity of the RPV model, it is difficult to directly solve the optimal trajectory tracking problem of RPV based on the original model.In Ref.11,a set of linear models is first established based on the trajectory linearization method, and a tracking controller is obtained by synthesizing a series of Linear Quadratic Regulators (LQR). Rehman employed the feedback linearization method and LQR for the trajectory tracking of AHV.12A Model Predictive Control (MPC) method was proposed in Ref.13for tracking the trajectory of LV. In this method, the simplified model of the original RPV model was derived based on the Taylor expansion,and the optimal tracking controller was obtained. Various applications of MPC in the field of RPV trajectory tracking have emerged, such as the RPV3guidance method and the guidance method of tactical missiles.14It should be noted that the above control methods are model-based. The dynamic model is needed for controller design. Furthermore, they are usually developed based on an affine RPV model; however, for some specific types of vehicles,an affine RPV model is not always available,such as solid rocket propelled RLV.

To solve the above problems,this paper studies the optimal trajectory tracking method under the condition that the accurate model of the RPV is not available under the framework of Adaptive Dynamic Programming (ADP). Based on the Value Function Approximation (VFA) idea (to solve the curse of dimensionality by estimating the value of the current control)15,16and dynamic programming theory(to derive the optimal control according to the value function),17the ADP was first proposed to solve the optimal control problem of complex systems in Ref.18. Compared with the traditional control approaches like the NDI, LQR, MPC and so on, ADP possesses two merits. One is that ADP is a data-driven control approach that is partially19,20or totally(if a data-based model can be established)21model-free. The other is that the parameters of the ADP controller are updated over time when the system is suffering from disturbances.The Actor-Critic Design(ACD)22is the most widely used ADP schemes. Two NNs are typically involved in the ACD. One is the critic NN designed for estimating the value of the current control, and the other is the actor NN designed for updating the control policy according to the output of the critic NN. Numerous ADP algorithms based on the ACD scheme have been proposed,such as global DHP and action dependent global DHP,22,23off-policy ACD,24,25etc. Recently, the adaptive optimal control methods based on the ACD scheme have already been successfully applied to the aerospace field gradually.26-28In Ref.29proposed a model-dependent ACD based adaptive optimal tracking controller for AHV.

Note that the ACD involves the iterative training between the actor NN and critic NN to converge to the optimal control policy.30Consequently, the ACD takes longer time to converge compared with the Single Network Adaptive Critic(SNAC) proposed in Ref.31and further developed in Refs.32,33. In SNAC, the actor NN is eliminated. Therefore,SNAC is an improvement to the dual network framework.Hence, the SNAC architecture offers three potential advantages: simpler architecture, lesser computational load, and no control policy approximate error for the control policy is not approximated by the action NN.34,35. So far, it has already been applied to the airplane flight control30and spacecraft attitude control.36These advantages are ideal for RPV trajectory tracking control. However, the SNAC can only be applied to the control-affine systems, while the dynamic models of the RPV are typically non-affine, such as the model of solidrocket-powered RLVs. An affine model is required to apply SNAC to the RPV trajectory tracking control. The dynamic NN based system identification approach provides a promising way to solve this problem.37As long as the data on the state variables and control input of the system is available, this approach can establish an approximate model for a real system through data-driven online identification.38,39The dynamic NN based identification approach is suitable to approximate the dynamics of systems subject to modelling uncertainties and external disturbances.

Inspired by the above elegant works, this paper studies the endo-atmospheric optimal trajectory tracking problem of Solid-Rocket-Powered Vehicles (SRPV) subject to aerodynamic disturbances.Since the ascent dynamic model of SRPVs is nonlinear and non-affine, the problem studied in this paper is actually the optimal control problem of uncertain nonlinear non-affine systems. The current optimal control methods based on ADP framework are mostly model-based. We aim to develop an adaptive optimal trajectory tracking control method which does not rely on the dynamical model of SRPVs. Furthermore, in order to simplify the pre-launch design process, it is desirable that the proposed controller can adaptively converge from an admissible controller to an approximate optimal controller. The design of the SRPV’s admissible controller is much easier than the optimal controller. In addition, considering the limitation of the computing power of SRPV in practical applications, a simpler design scheme is needed to reduce the burden of online computing. The main contributions of this paper lie in the following:

(1) This paper presents a model-free SNAC design method.The proposed method is designed in a model-free manner and therefore can be applied to both affine and non-affine systems. It overcomes the limitation of the traditional SNAC method that can only be applied to affine systems. Besides, the model-free design enables the proposed method to handle the model complexity of SRPVs and aerodynamic disturbances during endoatmospheric flight.

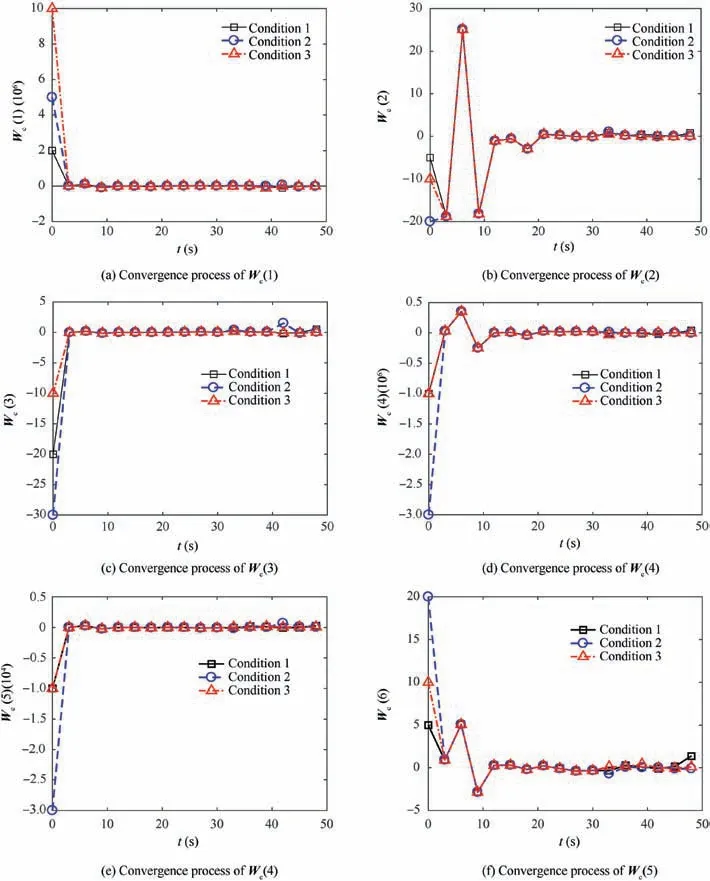
Fig. 2 Convergence process of critic NN weights.

Table 3 Control gain parameters and initial simulation conditions.

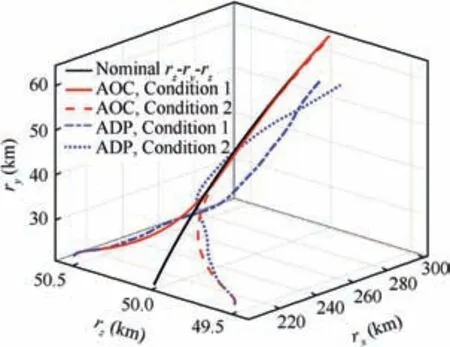
Fig. 3 Responses of rx-ry-rz.

Figs.4(c)and(d)shows the responses of the required guidance commands. The required guidance commands of the ADP-based method, especially the yaw angle, are always fluctuating. Combining Eq. (4) and Fig. 5, one can see that this is because the critic NN weights of ADP-based method cannot converge and are always fluctuating. However, the fluctuation of the required guidance commands of the AOC results from the updates of the critic NN weights which converge to approximate optimal values after several iterations.

Fig. 5 shows the online training process of the critic NN weights.We can see that the initial weights are significantly different from the optimal weights. Second, the AOC converges to the approximate optimal control policy after only 5-6 iterations. Thus, the pre-launch design only needs to provide an admissible control policy which is simple for the controller design of SRPV. Then the optimal control policy can be obtained online through online self-learning, which may be quite intriguing for practical applications.Note that Corollary 1 and Theorem 2 guarantee that a better policy can be obtained after each iteration, and the stability of the closedloop system is thus guaranteed even before the optimal policy is learned.

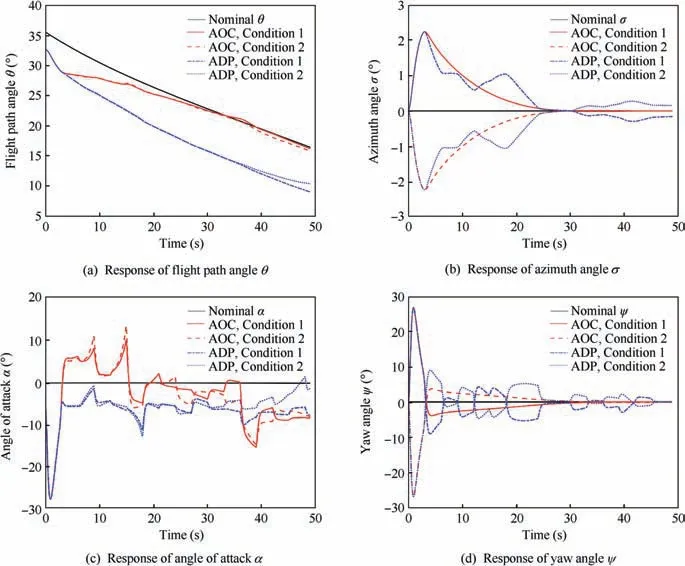
Fig. 4 Responses of the state and control variables.

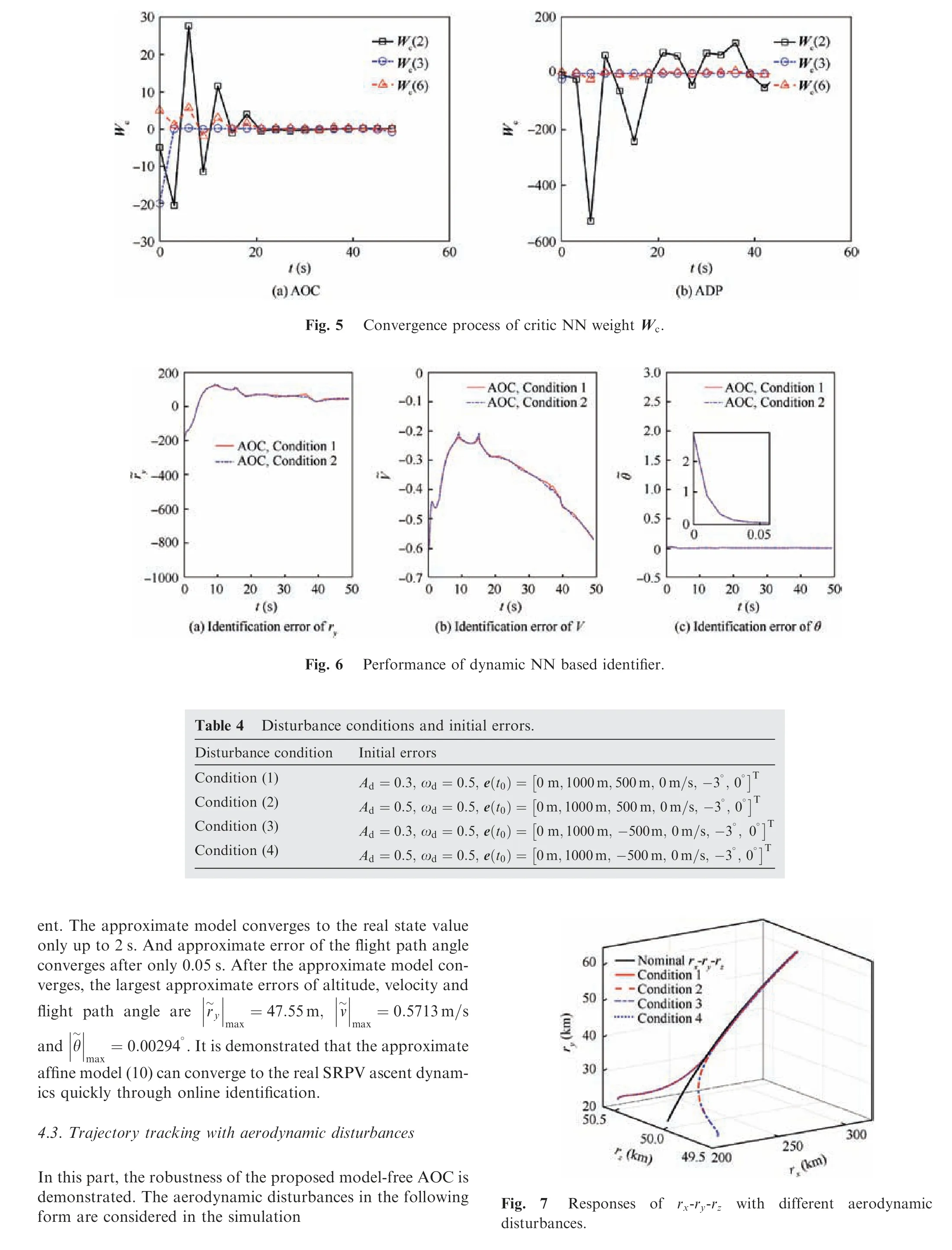
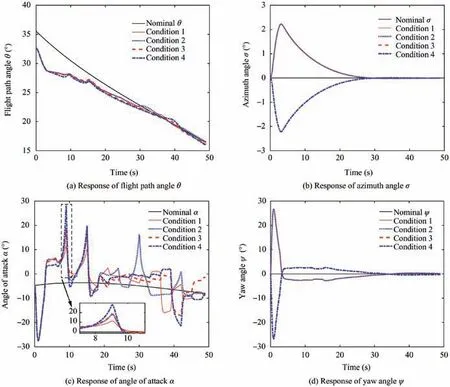
Fig. 8 Responses of the state and control variables with different aerodynamic disturbances.

where δF stands for the disturbance of the aerodynamic force.Adand ωdare the amplitude and frequency of the disturbances, respectively. All the other design parameters of the AOC are the same as the above simulation.

The following four conditions shown in Table 4 are considered in this part.

From Figs.7 and 8,we can see that even if up to 50%aerodynamic disturbances are introduced into the system, the proposed AOC can guarantee the trajectory tracking performance of the SRPV. Meanwhile, as shown in Figs. 8(c) and (d), the response of the required angle of attack and yaw angle are always within a reasonable range. The largest angle of attack and yaw angle are α| |max=28.06°and ψ| |max=26.8°,respectively.

Fig. 9 shows the online training process of the weights of the critic NN under different aerodynamic disturbances. The training process demonstrates that AOC can update the control policy to converge to the optimal one according to the online data of the system, which demonstrates the selflearning ability of the AOC. The convergence process takes up to 6-7 iterations (about 18-21 s).

Fig. 10 shows the identification results of the affine model,which shows that the identification performance is not influenced by the disturbance.

5. Conclusions

This paper presents a model-free SNAC design method for the trajectory tracking problem of SRPVs with uncertain nonlinear non-affine dynamics. In the proposed method, only the data of state and control variables, rather than the accurate mathematical model, of the SRPV are required for controller design. A closed-form adaptive optimal controller for the SRPV trajectory tracking problem is obtained with the proposed method. The first advantage of this design is that only one critic NN is involved in the controller.Thus,the complexity of the control system and online computation burden are simultaneously reduced.The second advantage is that starting from an initial admissible controller, the proposed controller can converge to an approximate optimal controller through online self-learning. Moreover, the model-free design and the self-learning learning property guarantee the disturbance rejection performance of the obtained controller.These advantages are suitable to solve the trajectory tracking of the SRPV subject to significant aerodynamic disturbances. And the uniformly ultimate boundedness of the trajectory tracking errors is guaranteed. The simulation results demonstrate the online convergence property and the trajectory tracking performance of the proposed controller.

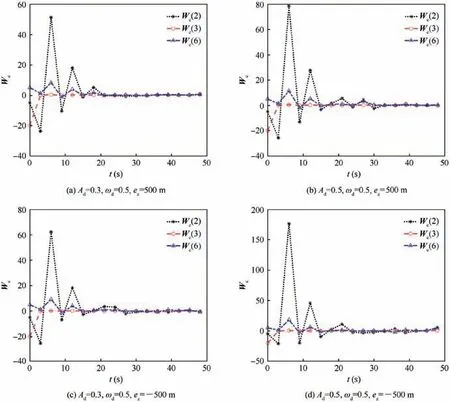
Fig. 9 Convergence process of critic NN weight Wc with different aerodynamic disturbances.

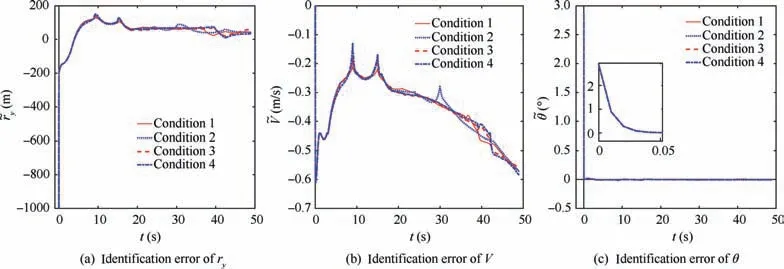
Fig. 10 Performance of dynamic NN based approximate model.

Acknowledgement

This work is supported by the National Key R&D Program of China (No. 2016YFB1200100).