Fluid structure interaction simulation of supersonic parachute inflation by an interface tracking method
Xue YANG, Li YU, Min LIU, Haofei PANG
a College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
b Engineering Design Center, China Electronics Technology Group Corporation No.10 Research Institute, Chengdu 610036, China
c Key Laboratory of Aircraft Environment Control and Life Support, Ministry of Industry and Information Technology,Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China
d 505 Institute, China Academy of Space Technology, Beijing 100089, China
KEYWORDS Contact method;Fluid structure interaction;Inflation dynamics;Numerical simulation;Supersonic parachute
Abstract An Arbitrary Lagrangian-Eulerian(ALE)approach with interface tracking is developed in this paper to simulate the supersonic parachute inflation.A two-way interaction between a nonlinear finite element method and a finite volume method is accomplished. In order to apply this interface tracking method to problems with instantaneous large deformation and self-contact, a new virtual structure contact method is proposed to leave room for the body-fitted mesh between the contact structural surfaces.In addition,the breakpoint due to the fluid mesh with negative volume is losslessly restarted by the conservative interpolation method. Based on this method, fluid and structural dynamic behaviors of a highly folded disk-gap-band parachute are obtained.Numerical results such as maximum Root Mean Square(RMS)drag,general canopy shape and the smallest canopy projected areas in the terminal descent state are in accordance with the wind tunnel test results. This analysis reveals the inflation law of the disk-gap-band parachute and provides a new numerical method for supersonic parachute design.
1. Introduction
With the rapid development of aeronautic, astronautic and weapon, work conditions of parachutes have extended from subsonic speeds to supersonic speeds. Researches on supersonic parachutes have been a hotspot in recovery and landing.Inflation is the most complex and critical stage in the working process of parachutes. However, the academic researches of the supersonic parachute inflation could not keep up with the development in engineering. Earlier studies are based on semi-empirical models to predict the shape and stress of the canopy. The typical models are four-stage inflation model,1stress model2and dynamic inflation model.3They are always used for the preliminary design of supersonic parachutes.Since the inflation process is highly nonlinear and unsteady, these greatly simplified models generally rely on empirical parameters and have low accuracy.
Fluid-Structure-Interaction (FSI) simulation is important for parachute design and verification.Some FSI methods have been maturely applied for subsonic parachutes,such as Simple Arbitrary Lagrangian-Eulerian (SALE) method4-8and Deforming-Spatial-Domain/Stabilized Space-Time (DSD/SST) method.9-13SALE method is employed firstly in Ref.14 to solve the inflation process of a disk-gap-band parachute at a freestream Mach number from 2.0 to 2.5.It has high accuracy in predicting drag coefficient and canopy shape,but nonphysical shock wave breakage phenomenon may occur in the flow filed. Compared with the subsonic parachute, there are some difficulties in the FSI calculation of supersonic parachute inflation. (A) The accuracy of the fluid model should be improved because bow shocks have a great influence on the numerical results. (B) Interaction between the capsule wake and canopy bow shock make the deformation of the canopy more complex. (C) The velocity of the incoming fluid is much larger than that of the subsonic parachute,so the deformation of the canopy is larger in the same amount of time.Due to the difficulties mentioned above, many scholars have modeled the supersonic parachute in terminal decent state as a transition.As the Eulerian approaches develop, they have been widely used for the computation of the supersonic parachute in terminal descent state. The typical methods are Ghost Fluid Method (GFM)15and Immersed Boundary Method (IBM).16In GFM, a level set technique is employed to represent the solid boundary in the Cartesian fluid solver. The breathing phenomenon of a disk-gap-band parachute is investigated by GFM in Ref.17. As for IBM, the boundary of the flexible canopy is computed in accordance with the relationship between the fluid and virtual cells.The influence of suspension lines,canopy attack angle and capsule attack angle on a hemisphere parachute system is studied based on IBM.18-20These Eulerian approaches have not been applied in the parachute inflation so far.
ALE approaches with interface tracking are the oldest and most commonly used method for FSI models with small deformation, including aeroelastic problem21-23and blood flow.24-26It is also applied to analyze the inflation process of a 2D supersonic parachute.27In the 2D simulation, the structural dynamic is modeled by Mass Spring Damper (MSD)method28-30which disperses the parachute into a series of mass points connected by the springs and dampers. Dynamic mesh methods containing spring-based smoothing and local remeshing are employed to update the fluid mesh. It has not been extended for the 3D supersonic parachute inflation because current dynamic mesh and contact method are not mature enough.The updated fluid mesh by the dynamic mesh method gradually declines in quality as the calculation proceeds.Number of time steps for the inflation process is much larger than that for the terminal decent state.When sudden large deformation occurs at the mesh with large skewness, the calculation would terminate due to the mesh with negative volume. In addition, when conventional contact methods are applied,the distance between the contact structural surfaces tends to zero or even negative. Thus, there is no room for the generation of the body-fitted fluid mesh.
In this paper,an interface tracking method is firstly used for the 3D FSI simulation of the supersonic parachute inflation.A nonlinear finite element method is coupled with a finite volume method. In the Computational Structural Dynamics (CSD)solver,suspension lines and canopy are modeled as one dimensional linear elastic material and Kirchhoff material respectively. In order to prevent the body-fitted mesh between the contact structural surfaces from excessively compressed, a new contact method is proposed. The element is projected on the virtual contact region to calculate the contact force by penalty function method. In the Computational Fluid Dynamics(CFD) solver, the preconditioned dual time stepping scheme is employed to provide time-accurate solution of unsteady parachute aerodynamic analysis. At the breakpoint of the FSI simulation,the fluid mesh is regenerated by global remeshing method.And the breakpoint is losslessly restarted by mapping flow parameters onto the new mesh and initializing the CSD solver by the numerical results obtained at the breakpoint. A typical disk-gap-band parachute is modeled in this paper to test the ability of this FSI method. The accuracy of this method is verified by the wind tunnel test results. The inflation law of the supersonic parachute is discovered.
2. Mathematical model
2.1. Structure dynamics
2.1.1. Governing equations of structure system
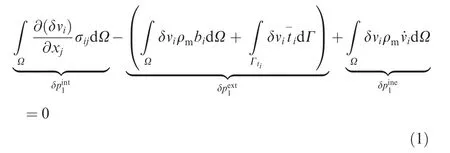
Basing on principle of virtual work,the governing equation of structure system is31
Suspension lines and reinforcing bands are simulated as one dimensional linear elastic material,

where E is the Young’s modulus,ε is the strain.The canopy is simulated as Kirchhoff material, which is used to describe the large rotation and small strain of the fabric during inflation,32

where J is the Jacobian matrix, E is the Green strain, S is the PK2 stress,

where C is the fourth order elastic tensor. The material of the canopy is assumed to be continuous,homogeneous and isotropic linear elastic material.3-node shell elements are used in the simulation. Thus, the PK2 stress can be simplified as


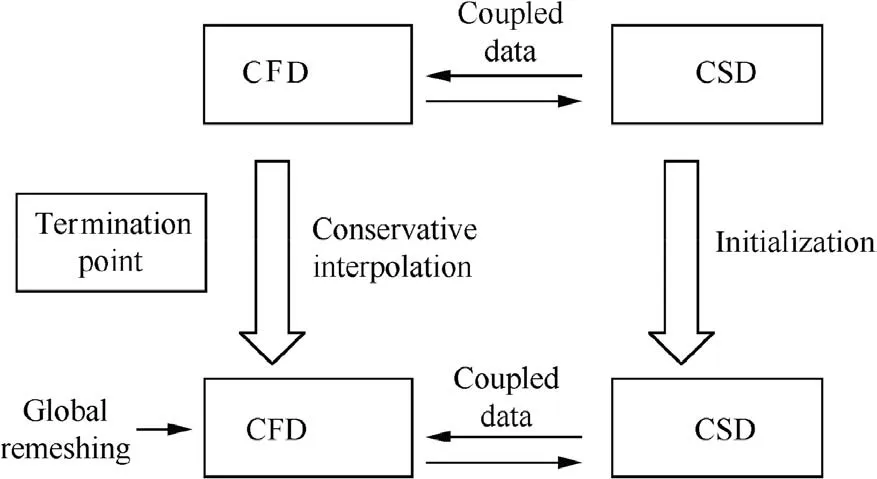
Fig. 3 Restart of a breakpoint.
where ΔV is the swept volume by the surface during time step Δt, Sdis the area of the surface. For variable topology mesh,the flow field parameter of the new mesh is calculated by the conservative interpolation method,37

Where Anewis the contribution of the new mesh,wiand Aiare the flow parameters and contribution of the ith subdomain.The subdomains are parts of the new mesh divided by the old mesh.
3. Geometric and numerical model
A disk-gap-band parachute used in the wind tunnel test39is investigated for numerical study. Its main geometric parameters are shown in Fig. 4.
This study has performed a 3-D simulation to investigate the supersonic flow over a flexible parachute model at a freestream Mach number of 2, dynamic pressure of 16.8 kPa and Reynolds number of 1.0×106. Under condition of infinite mass, the inflation process of the supersonic parachute is simulated.As shown in Fig.5(a),the initial structural mesh model of the parachute is constructed by the direct folding modeling technology. The suspension lines and canopy are assumed to be completely straight. The canopy looks like a carambola from overlooking.The constraint of the parachute is in accordance with the constrained case in the wind tunnel test. The canopy is meshed by 11472 triangular shell elements. The suspension lines and reinforcement belts are meshed by 3720 twonode bar elements.The Young modulus,Poisson ratio,density and thickness of the canopy are 8.8×109Pa, 0.14, 375 kg/m3and 1.3×10-4m respectively. The Young modulus and density of the suspension lines are 4.3×1010Pa and 412 kg/m3respectively.Fig.5(b)shows the fluid mesh model of the parachute system, where D0is the nominal diameter of the parachute system. The flow field is discretized using 402075 tetrahedral elements in Region 1 and 361088 hexahedral elements in Region 2. The dynamic mesh method is only used in Region 1 to save computing resources. And there are 8320 pyramid elements between the two regions.Nonslip,adiabatic boundary conditions are imposed on the canopy and capsule.The pressure-far-field condition is imposed on the flow field boundary.The global remeshing method and the virtual structure contact method are accomplished by the secondary development of according commercial softwares. As shown in Table 1, the effect of the time step on the number of breakpoints is studied. With the decrease of the time step size, the number of breakpoints first decreases and then keeps stable.There is a turning point at about 1×10-5s for the time step.So it’s selected as the time step for the following simulation to reduce the number of breakpoints and computational cost.This coupling calculation is carried out by the DELL T5500 workstation with 12-core, 32 G memory. The CPU time consumption is about 101 h.
4. Verification of the virtual structure contact method
In order to investigate the influence of the new contact method on the numerical results, the virtual structure contact method and the conventional penalty function contact method are used in the structural simulation of the parachute inflation.Without FSI simulation, uniform pressure with a value of 13,000 Pa is imposed on the internal surface of the canopy to replace the fluid pressure. Fig. 6 shows the top view of the band shape at 1 s. The virtual contact region in the new contact method ensures that the distance between the contact canopy elements equals to the size of the local mesh. On the contrary, the distance between the contact canopy elements tends to zero or even negative by using the conventional penalty function contact method.

Fig. 4 Geometric model of the disk-gap-band parachute39.
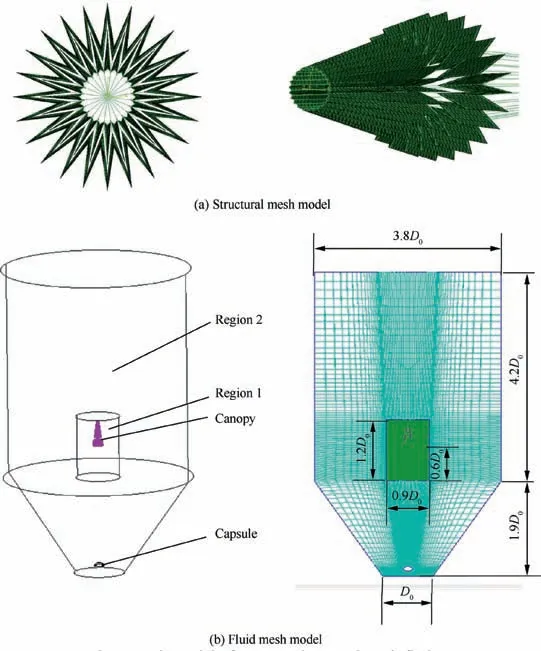
Fig. 5 Mesh model of the supersonic parachute inflation.

Table 1 Effect of the time step on the number of breakpoints.
Figs.7 and 8 compare the canopy stress and projected area spobtained by the virtual structure contact method and conventional penalty function contact method respectively. Due to the symmetry of the parachute initial shape, external force and constraint,the deformation of the canopy is also symmetrical.In the inflation process,the stress on the disk is much larger than that of the band. The maximum stress is close to the vent.The projected area of the canopy increases exponentially.The projected area calculated by the virtual structure contact method is larger than that calculated by the conventional penalty function contact method with a maximum error of 7.4%.It is found that the canopy shape, projected area and stress obtained by these two contact methods are similar. The existence of the virtual contact region increases the symmetry of the canopy stress. This new contact method has the similar work effect with the conventional penalty function contact method to model the contact force and stress. The conventional penalty function contact method is a mature and widely used method in contact problem. So, the comparison of the two contact methods proves that the distance between the contact elements has little influence on the work effect of contact calculation.
5. Results and discussion
5.1. Application effect of the virtual structure contact method
As shown in Fig.9,the band at 0.0013 s is used as an example to reveal the application effect of the virtual structure contact method. In the inflation process, the radially folded canopy gores approach each other gradually. When the distance is smaller than the size of the local fluid mesh, contact force starts to impose on the canopy due to the existence of the virtual contact region.Fig.9(a)shows the stress of the band from two perspectives. Contact stress is produced at the canopy when there seems a distance between the gores. Since the new contact method prevents the body-fitted flow field mesh from being excessively compressed, the fluid mesh is good enough for FSI simulation (Fig. 9(b)).
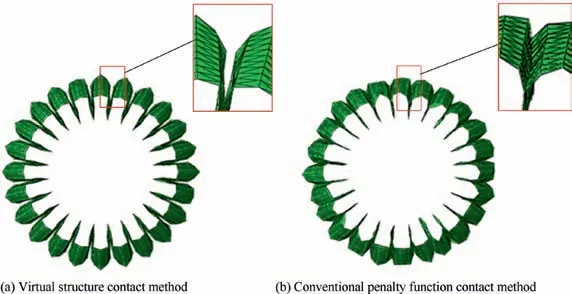
Fig. 6 Top view of the band shape at 1 s.
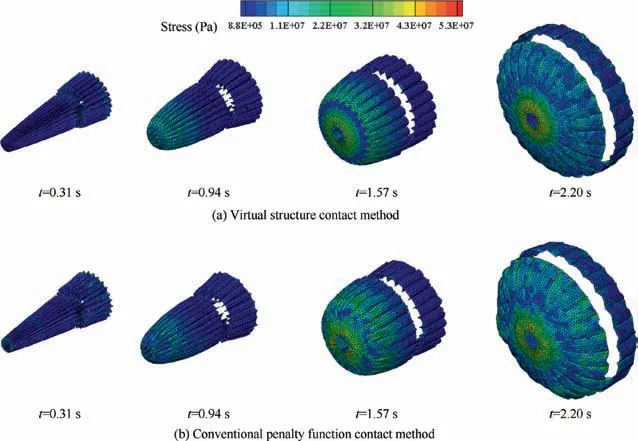
Fig. 7 Canopy stress in the inflation process.
5.2. Comparison of numerical and experimental results
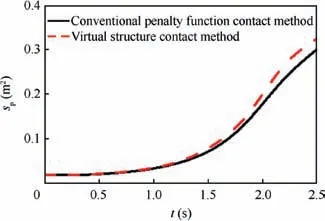
Fig. 8 Projected area of the canopy.

Fig. 9 Stress and fluid mesh of the band at 0.0013 s.

Fig. 10 Comparison between numerical result and experimental data39 for RMS drag.
Fig.10 compares the RMS drag F in the numerical simulation and wind tunnel test.39The value and occur time of the maximum RMS drag are 6757 N and 0.013 s in the numerical simulation, which are larger than the wind tunnel test results(6504 N and 0.012 s respectively). The parachute of the wind tunnel test is folded in the pack while the parachute of the numerical simulation is assumed to be completely straight.The initial projected area of the numerical simulation is much larger than that of the wind tunnel test. So in the initial stage of the inflation,the RMS drag of the numerical results is much larger. In addition, the canopy is made of flexible fabric with low density. The inflation status of the canopy is highly affected by the unsteady fluid.The vortex structures in the real fluid is more random than that in the numerical simulation.So the oscillation amplitude of RMS drag in the wind tunnel test is more random after the canopy is fully inflated. Figs.11 and 12 show the projected area spand shock wave standoff distance of the canopy d in the numerical simulation. The projected area of the canopy near-linearly increases firstly. Then the slope of the curve increases suddenly and then the projected area reaches the peak. Finally, the projected area decreases rapidly after the peak and oscillates periodically in the terminal descent state.The smallest canopy projected areas in the terminal descent state of the wind tunnel test and numerical simulation are 0.246 m2and 0.265 m2respectively. The curve of the shock wave standoff distance has two peaks.One is at 0.012 s, and the other is at the moment when the maximum projected area occurs. The valley is at the moment when the maximum RMS drag occurs.
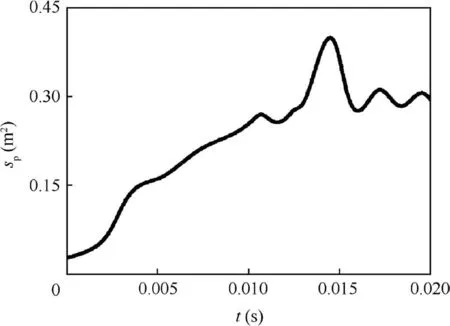
Fig. 11 Projected area of the canopy.

Fig. 12 Shock wave standoff distance of the canopy.
Fig. 13 indicates three instants of the canopy shape in the inflation process of the disk-gap-band parachute.39The projected area and general shape of the canopy in the numerical simulation are in accordance with the wind tunnel results.The canopy shape is more symmetrical and collapse of the band has not been reproduced in the numerical simulation because the action of turbulence pulsation to the flow field is neglected.
5.3. Flow and structural filed of the inflation process
As shown in Fig. 14, seven typical moments of the inflation process are chosen to analyze the flow and structural field.The canopy has small projected area in the initial stage,so only little incoming fluid entries into the canopy.There is no vortex internal the canopy at this moment(Fig.14(b1)).Then the disk starts to inflate firstly (Fig. 14(c2)). With the expansion of the disk skirt,the excess of inflow over outflow goes into storage in the canopy. A pair of vortices generate at the disk and band respectively (Fig. 14(b2)). The connecting lines between the disk and band drive the inflation of the band. The expansion rate of the upper skirt of the band is greater than that of the bottom skirt(Fig.14(c3)and(c4)).Next,the two pairs of vortices combine into one pair of vortices. The wake vortex area starts to take shape (Fig. 14(b3) and (b4)). At 0.013 s, the canopy has the maximum RMS drag, internal pressure and disk stress (Fig. 14(a5) and (c5)). At 0.015 s, the canopy has the maximum projected area, maximum shock wave standoff distance and smallest internal pressure. The overstretched band has the maximum stress(Fig.14(c6)).Finally,the canopy rebounds to the working diameter because of the bounds of suspension lines. The canopy is not completely symmetric inflated in result of the asymmetric flow (Fig. 14(a7) and(c7)). The stress in the terminal descent state is much smaller than that in the inflation process (Fig. 14(c7)).
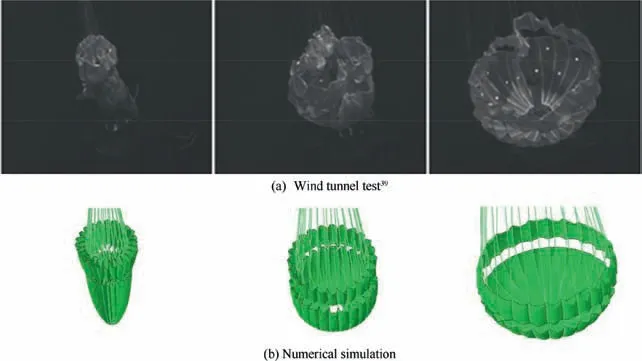
Fig. 13 Canopy shape in the inflation process.
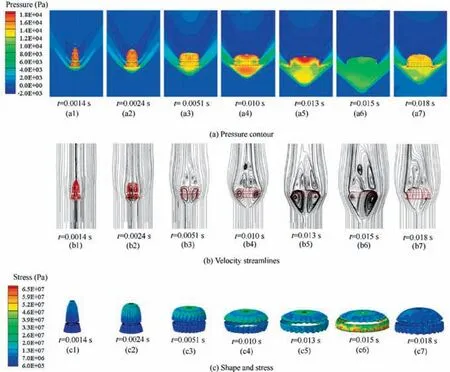
Fig. 14 Flow and structural filed around the canopy in the inflation process.
6. Conclusions
1) An ALE approach with interface tracking is used for simulation of the supersonic parachute in the inflation process. Time-sequence change of the canopy shape and aerodynamic characteristics of parachute can be predicted by this FSI method.
2) The virtual structure contact method leave room for the body-fitted mesh between the contact structural surfaces. It ensures the good quality of the fluid mesh between the contact structural surfaces. Thus this interface tracking method can be used for problems with selfcontact.
3) The conservative interpolation method is very effective to map the flow parameters on the newly generated mesh.Since the fluid and structural parameters are continuous at the breakpoint,this interface tracking method can be used for problems with instantaneous large deformation.
4) The numerical results are consistent with the experimental results.It proves the validity of the method proposed in this paper. This method can be potentially used for material selection and performance predication during supersonic parachute design.
Acknowledgements
This work was co-supported by National Nature Sciences Foundation of China(Nos 11972192,11172137)and A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
 CHINESE JOURNAL OF AERONAUTICS2020年6期
CHINESE JOURNAL OF AERONAUTICS2020年6期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- A novel variable structure multi-model approach based on error-ambiguity decomposition
- Multi-block SSD based on small object detection for UAV railway scene surveillance
- A new online modelling method for aircraft engine state space model
- Cross-sectional deformation of H96 brass double-ridged rectangular tube in rotary draw bending process with diあerent yield criteria
- Application of a PCA-DBN-based surrogate model to robust aerodynamic design optimization
- Numerical exploration on the thermal invasion characteristics of two typical gap-cavity structures subjected to hypersonic airflow
