A new structural reliability analysis method in presence of mixed uncertainty variables
Lingfei YOU, Jianguo ZHANG,*, Xiaosong DU, Jie WU
a School of Reliability and Systems Engineering, Beihang University, Beijing 100083, China
b Science and Technology on Reliability and Environmental Engineering Laboratory, Beihang University, Beijing 100083, China
KEYWORDS Automatic updating strategy;Extreme response surface;Membership function;Mixed uncertainty;Particle swarm optimization;Structure reliability
Abstract For structures with both random and fuzzy uncertainty, this paper presents a novel method for determining the membership function in fuzzy reliability with the Automatic Updating Extreme Response Surface(AUERS)method.In the proposed method,fuzzy variables are initially converted into a value domain under the given cut level and the extreme point in the domain where the reliability reaches its extreme value is considered. Second, the Particle Swarm Optimization(PSO)algorithm is used to determine the extreme point according to the extreme responses for different sets of random sample inputs. A kriging response surface is subsequently constructed between the random variables and the corresponding extreme points.An automatic updating strategy is then introduced based on the Relative Mean Square Predicted Error (RMSPE) before performing every iteration of reliability analysis. By adding new sample points, the approximate quality of the kriging response surface is improved.Finally,reliability analysis is used to determine the reliability bound under the given cut level.The proposed method assures the accuracy and computation efficiency of the mixed uncertainty reliability analysis results while it prevents the solution from becoming trapped in a local optimum, which occurs in classical optimization methods. Two example analyses are used to demonstrate the validity and advantages of the proposed method.
1. Introduction
Structural reliability analysis requires addressing all sources of uncertainty. To design reliable products, different forms of uncertainty in engineering provide a challenge for reliability analysis and carry higher requirements on uncertainty analysis.Uncertainty can be classified into two types: aleatory uncertainty and epistemic uncertainty. Typically, aleatory uncertainty is modeled as random variables while epistemic uncertainty can be modeled using nonrandom variables like possibility membership functions or intervals. Aleatory uncertainties in reliability analysis have been successfully handled by using probability theory, which requires complete statistical information and a probability distribution to describe these aleatory uncertainties. Fuzzy theory can be used to represent the available data in an analytical form for situations where sufficient information is not available for defining a probability distribution.
Reliability analysis involves defining aleatory uncertainty with a limit state function, which is estimated in terms of the probability that a structural response exceeds a threshold limit.1,2Probabilistic reliability analysis methods with random variables include three classes: moment-based, simulationbased, and surrogate model-based methods. In the first case,the moments of the variables are used to estimate the reliability probability, which requires the gradient of the limit state function. These methods are popularly known as First or Second-Order Reliability Methods (FORM/SORM).3-6Simulation-based methods strive to produce an acceptable approximation of reliability by sampling from the limit state function. These includes direct Monte Carlo sampling,7,8importance sampling,9directional sampling,10and line sampling.11,12As an alternative, response surface techniques have also been used for reliability analysis.13,14As a highly efficient reliability method for high high-dimensional and smallreliability probability problems, the advantages of the Nested Extreme Response Surface (NERS) method have been fully proven in the literature.15,16
In contrast to aleatory uncertainty, epistemic uncertainties are based on subjective perception, imperfect modeling, and limited data availability, such as interval analysis, possibility theory, and fuzzy set theory. Fuzzy set theory is widely used in the field of reliability analysis. Dong and Wong17proposed a computational algorithm based on the α-cut representation of fuzzy sets. Khaniyev et al.18presented some mathematical operators that can be easily applied to type-2 fuzzy numbers,and the mathematical functions of the type-2 fuzzy numbers are given according to their monotonicity. Li and Nie19proposed a fuzzy reliability calculation method based on the error synthesis principle for fuzzy random uncertainty inputs.Wang et al.20proposed useful methods for determining membership functions and developed a structural reliability analysis method based on the fuzzy safety state. Bagheri et al.21used Particle Swarm Optimization (PSO) to determine the extreme members of a reliability index interval, and the importance sampling technique was used for reliability analysis.
These aforementioned methods consider a single uncertainty. However, in most problems, aleatory and epistemic uncertainties may exist simultaneously, where some variables have a probability distribution and some have a membership function. Therefore, hybrid reliability analysis has been extensively studied, which considers random and fuzzy variables simultaneously. Shi et al.22involved both random and fuzzy inputs,and two indices,called the fuzzy time-dependent failure probability and the random time-dependent failure possibility,were presented to measure safety degree of time-dependent structure from different aspects. Wang et al.23proposed a physics-based reliability analysis method that considers the merits of both the Saddle-Point Approximation (SPA)-based simulation method and the fuzzy random variable. Balu and Rao24proposed a structural reliability estimation method when the limit state function exhibits multiple design points by blending locally-constructed approximate functions.Ebenuwa and Tee25presented a numerical strategy for the efficient reliability assessment of engineering structures with random and fuzzy variables using a fuzzy-based optimised Subset Simulation(SS)approach.Nair and Sasikumar26examined the scope of profust reliability and the different working states of the reservoir are described as fuzzy states.The hydropower production is considered as a random fuzzy event based on the degree of success in meeting the power demand and randomness associated with inflows.Chen et al.27presented a calculation method for the dynamic fuzzy degree of reliability of bedding rock slopes under random earthquake excitation using the first excursion failure criterion, which considers uncertainties in the strength parameters and structural limit states.Chen et al.28proposed an iterative Structure-Adaptive Fuzzy Estimation(SAFE)for random-valued impulse noise suppression.The SAFE method was developed in the framework of Gaussian maximum likelihood estimation. Li and Lu29investigated a method for determining the bounds of structural reliability using nesting analysis of interval optimization. This was performed with modern heuristic methods, and a Line Sampling(LS) method in the reduced space of random variables is used for reliability analysis.Wang et al.30proposed a computational framework for system reliability analysis and optimization with simultaneous random and fuzzy uncertainties using safety assessment theory and the hybrid uncertainty propagation technique.
These methods can be roughly divided into three categories:transformation, iteration, and sampling methods. However,there are still some problems that have not been solved.When the structure involves high dimensional and nonlinear response,the iteration efficiency is not satisfied.Most sampling algorithms require inefficient screening the membership interval for fuzzy variables, and as the number of dimensions and degree of nonlinearity increase, the optimization method used in these methods will fall into a local optimum. The point of intersection with the limit state function must also be determined, which is tedious.





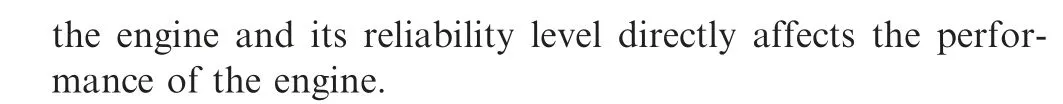
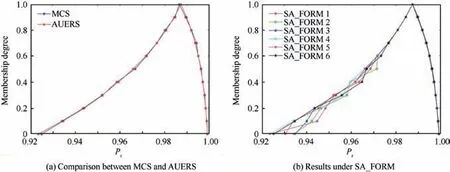
Fig. 6 Fuzzy reliability membership functions in Example 1.

Table 2 Computational costs of various methods for estimating reliability interval at given membership level.
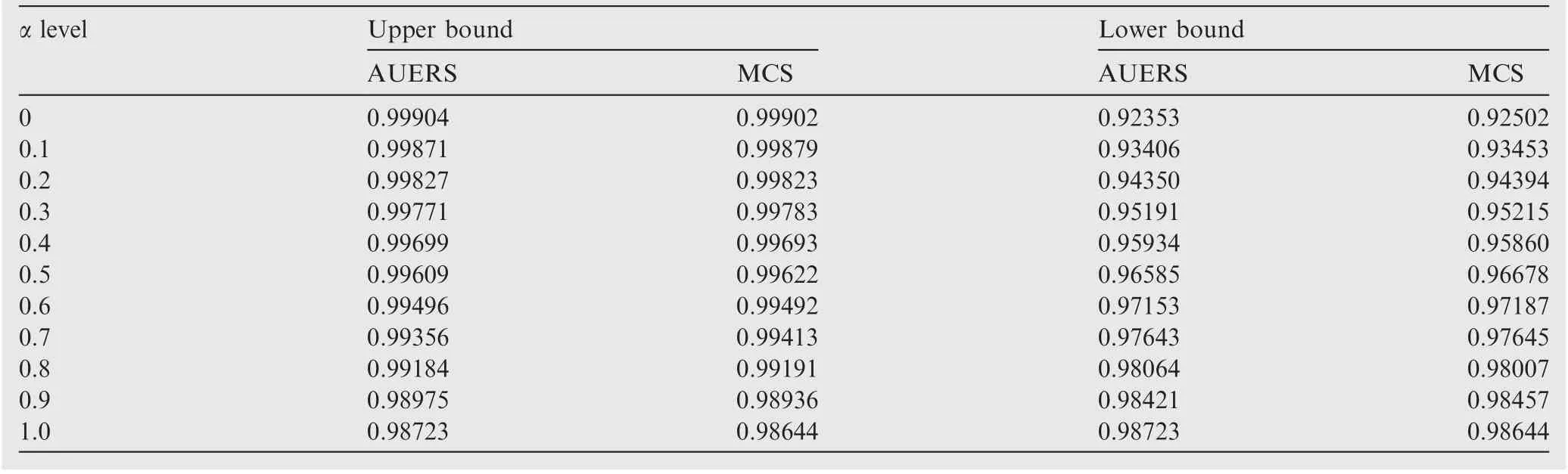
Table 3 AUERS reliability probability compared with MCS results.
In this study, a third stage roulette of a low-pressure compressor on a turbine disk is selected as an example,and the pin on the disk is evenly distributed along the circumferential direction. The main sources of parametric uncertainty include the randomness or fuzziness of the load and material. In this example, the average speed is 9550 r/min, the shaft material is 3Cr13, the wheel disk material is TC11, the blade load is applied to the pin shaft, and the mean resultant force is 29189.6 N.The details of the parameters are shown in Table 4,which are independent normal random variables. The speed ω (r ad/s) and resultant force P (N ) are fuzzy variables.

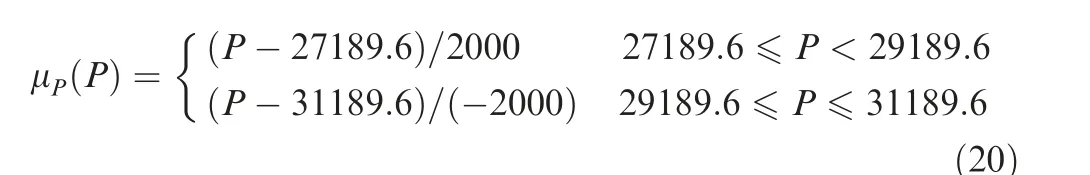
The reliability of a turbine disk depends primarily on the distribution of stress and strain at the dangerous point in the structure. Because the shape and load on the structure are completely symmetric, 1/37 of the roulette wheel is considered in this example. First, the mean values of each variable are chosen as parameters, and the simulation is implemented with ANSYS 18.1. The model is shown in Fig. 7 and the results of one simulation are shown in Fig. 8. The stress-strain level is highest at the junction of wheel disc and pin axis, which is the failure point of the structure. The maximum stress is 0.834×109Pa.
When the maximum stress at the dangerous point exceeds the allowable value Smaxas 0.845×109Pa, then the structurewill fail, and the corresponding limit state function can be expressed as follows:
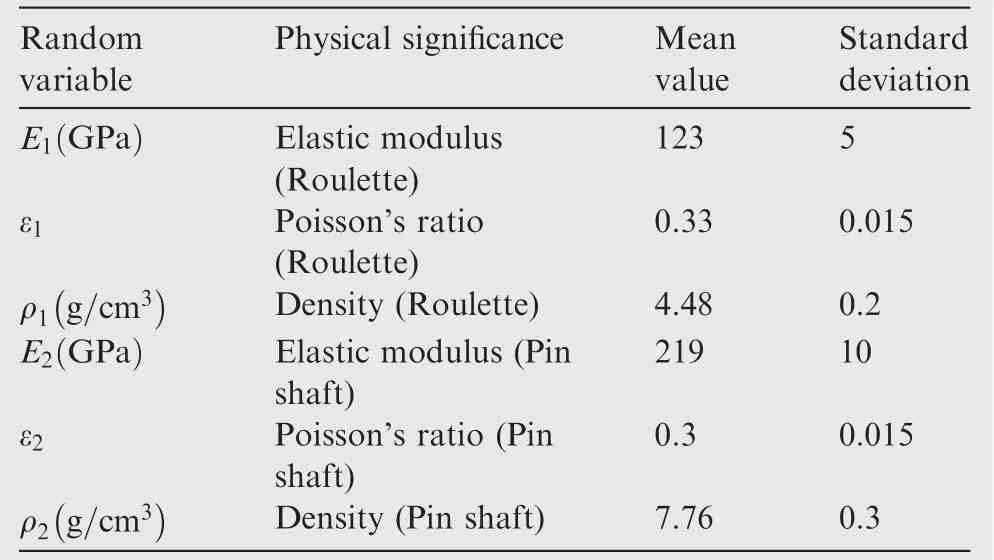
Table 4 Parameters of turbine disk.
Multi-point approximations were constructed for the limit state firstly because this is a problem with implicit limit-state functions. These approximations are used as closed-form expressions for estimating the bounds on reliability.The Latin hypercube sampling technique is used to sample 45 design points for the SA_FORM and AUERS methods. A comparison of the fuzzy reliability membership functions estimated with the various methods is shown in Fig. 9.
The results in Fig.9 show that the membership function for fuzzy reliability obtained with the proposed method is consistent with the MCS results in the nonlinear engineering example. The membership function for fuzzy reliability obtained using the AUERS method shows some discrepancy,and a relative error (relative to MCS method) comparison between the proposed method and the FORM based on SA is shown in Table 5. The maximum difference in the reliability estimated is less than 0.0933%.This illustrates the engineering applicability of the proposed method.
In each realization of the fuzzy variables, 106simulations are required with MCS for convergence,and 280 iterations are used in the SA_FORM method, whereas only 180 automatic update iterations are required on average in the proposed method. It is obvious that as the number of dimensions in the input parameters increased,the number of iterations increased greatly, but the proposed method is still highly efficiency.Moreover,a comparison of reliability probability relative error between the MCS results and those with the other two methods show that the results from the AUERS method do not sacrifice accuracy, and most of the results from the proposed method are consistent with those from the MCS.All relative errors of upper bound are smaller than those of SA_FORM method,some lower bound results are not because of the extreme convergence condition RMSPE is not small enough for finding the minimum, but the error range is not large, and it is satisfactory for the whole results. This engineering example illustrates the computational efficiency and accuracy of the proposed method.
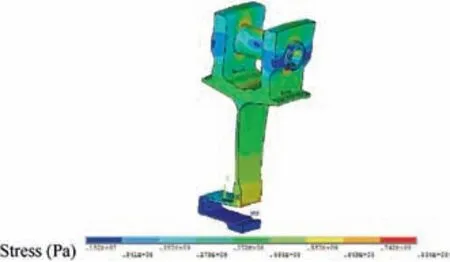
Fig. 8 Stress cloud chart of roulette at 9550 r/min.
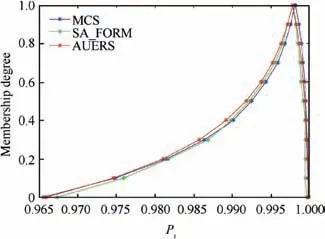
Fig. 9 Fuzzy reliability membership functions in Example 2.

Fig. 7 Model of roulette wheel.

Table 5 Relative error in reliability probability compared with MCS results.
5. Conclusions
An automatic updating extreme value response surface method is proposed for solving structural reliability problems with mixed random and fuzzy uncertainties. This method aims to couple reliability analysis with updating the extreme value points. The basic concepts and procedures in the AUERS method are introduced, and several examples illustrated its precision and efficiency. The proposed method can simultaneously avoid falling into a local optimum caused by traditional mixed uncertainty analysis methods and provide accurate results. In addition, it incurs lower computational cost when screening the membership interval. For the analysis of the updating progress, AURSE method can make full use of the advantages of PSO and the kriging model through a double loop strategy. To search extrema, the proposed method uses an automatic updating strategy in the reliability analysis instead of interval optimization algorithms.
AUERS method converts the mixed uncertainty problem into a random variable problem and improves the calculation stability for reliability with mixed uncertainty.Compared with a traditional method,such as SA_FORM for reliability analysis, the proposed method could provide satisfactory results,and its higher accuracy can further improve the optimization efficiency of the outer loop.
Finally, the different number of particles or termination thresholds in optimization produces small fluctuations in the results. Meanwhile, there may exist other methods that can be used to determine the extreme membership value because the inner loop and different approaches will lead to differences.The proposed method provides a general framework for reliability analysis with fuzzy and random uncertainties. This provides the potential for further improving the efficiency of the AUERS method.
Acknowledgement
This research was supported by the National Natural Science Foundation of China (No. 51675026).
 CHINESE JOURNAL OF AERONAUTICS2020年6期
CHINESE JOURNAL OF AERONAUTICS2020年6期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- A novel variable structure multi-model approach based on error-ambiguity decomposition
- Multi-block SSD based on small object detection for UAV railway scene surveillance
- A new online modelling method for aircraft engine state space model
- Cross-sectional deformation of H96 brass double-ridged rectangular tube in rotary draw bending process with diあerent yield criteria
- Application of a PCA-DBN-based surrogate model to robust aerodynamic design optimization
- Numerical exploration on the thermal invasion characteristics of two typical gap-cavity structures subjected to hypersonic airflow
