柔性透明薄膜掺杂微纳米粒子的光谱特性研究*
黄美娇
(中国科学院长春光学精密机械与物理研究所,长春 130033)
0 引言
柔性材料因对光谱具有可逆动态调控的特点而具有很大的应用潜能,例如:对光的透射性可调可应用到车窗设计;吸收性可调能够应用到墙体设计;发射性可调在隐身衣的设计和制造上具有重要价值。
国内外学者已经对柔性材料的光谱调控特性进行了大量研究。Kim等[1]设计了“M-Ink”,是一种具有弹性的材料,在磁场力作用下改变结构的周期性,从而使表面的光谱透射率和反射率发生改变。Zhu等[2]在水凝胶膜上开圆柱孔,外界水环境能够改变孔的大小,孔的大小影响光的透过性。Lee等[3]在褶皱的弹性体PDMS上镶嵌纳米线,构成一种可逆调控的光学窗口,通过拉力改变PDMS褶皱的程度使纳米线的倾斜角度发生改变,从而实现对光谱透射率的可逆调控。Park等[4]将材料为硅的纳米柱子周期性排列在聚二甲氨基硅氧烷薄膜中,通过机械力改变纳米柱子的排列周期,导致在结构表面的偏振角上发生改变,以此实现结构光学特性的可逆动态调控。Liu等[5]将W掺杂VO2的薄膜沉积在石英基底上,制备了一种W-VO2薄膜,在温度作用下,薄膜的发射率发生改变。Zhang等[6]用光学涂层技术得到一种Ge(高折射率材料)、ZnS(低折射率材料)交叉叠放到石英基底上的微结构,整个结构在3~5 μm和8~14 μm具有低发射率。Li等[7]研究了Sn中掺杂ZnO而成的薄膜结构的红外辐射特性。
聚二甲基硅氧烷(PDMS)是一种高分子弹性有机化合物,具有良好的透光性、化学稳定性和低杨氏模量等特性,在光学波导[8]、生物医学[9]和人造电子皮肤[10]等领域应用广泛。以PDMS作为基底,掺杂微纳米粒子,外界拉伸力能够调节其形变,从而实现光谱特性的可逆动态调控。
1 基本理论
1.1 建立模型
图1所示为掺杂粒子的PDMS薄膜模型,在柔性高分子透明材料PDMS中掺杂材料为Ni或Al2O3的微纳米粒子。由于Ni在0.3~2 μm波长范围内具有较强吸收性,Al2O3在0.4~0.8 μm波长范围内具有较强反射性,故在PDMS薄膜中分别掺杂Ni粒子和Al2O3粒子,能够使薄膜在0.3~2 μm范围内的吸收率和0.4~0.8 μm范围内的反射率发生改变。
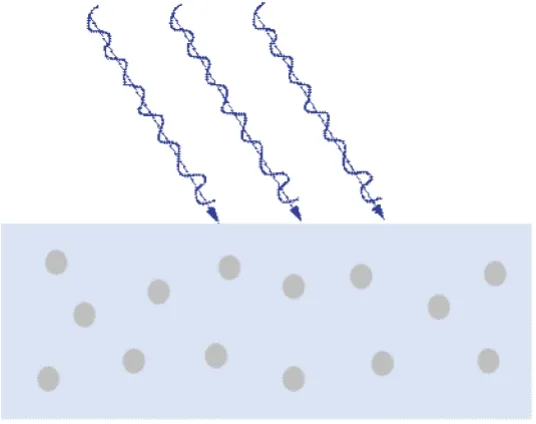
图1 掺杂粒子的PDMS薄膜模型
1.2 数值计算
本文先利用米氏散射理论计算出单个粒子的辐射特性,然后利用蒙特卡洛方法求解辐射传输方程,得到薄膜的辐射特性。
1.2.1 米氏散射理论
米氏散射公式是球形均质粒子对无偏振平面电磁波的麦克斯韦方程的远场解,远场解是从麦克斯韦方程的精确解简化而来的,其衰减因子、散射因子和散射相函数公式[11]分别为:

式中: χ为尺度参数;an与bn称为米氏散射系数。

式中:πn和τn称为散射角函数,二者皆和连带的勒让德多项式Pn有关。
利用米氏散射理论计算单个粒子的辐射特性。计算代码是在Modest[11]写的基础上修正得到的。
1.2.2 蒙特卡洛方法
本文所研究的粒子满足独立散射条件[12]。如果粒子半径为ri,Ni为单位体积薄膜中粒子的个数,则散射因子、吸收因子和散射相函数的计算式分别为:

式 中 : Qsca,i,Qabs,i和 Φ(ri,θ)由 式 (1) ~(3) 和 方 程Qext,i=Qabs,i+Qsca.i得出。
求解辐射传输方程[11]:

用蒙特卡洛方法求解辐射传输方程时,能量束的数量越多,越接近精确解。文中的每个算例用1 000 000个能量束,为验证所选取的能量束数量对蒙特卡洛方法的计算精度没有影响,本文设定薄膜厚度s=20 μm;掺杂的Ni粒子直径d=1 μm;体积分数 fV=1.5%。对能量束分别为1 000 000和10 000 000的2个薄膜模型的计算结果进行比较,发现两者的吸收率曲线吻合得很好,故1 000 000个能量束足以满足计算精度,如图2所示。本文用“散射或者反射能量份额分布[13-14]”方法来追踪能量束的路径。
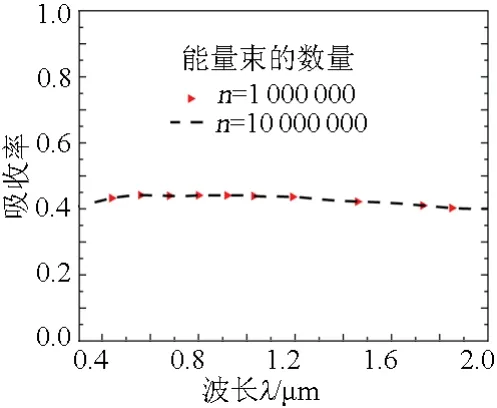
图2 能量束的数量对蒙特卡洛计算精度的影响
2 结果分析
2.1 粒径对光谱特性的影响
本节分别讨论了PDMS薄膜中掺杂Ni和Al2O3纳米粒子,粒径对薄膜模型光谱特性的影响。
2.1.1 Ni粒径
不同Ni粒径下的薄膜模型的光谱透射率和吸收率如图3所示,薄膜厚度s=20 μm,粒子的体积分数fV=1%。如图3(a)所示,薄膜模型的透射率在0.3~2 μm波段范围内随波长变化十分平缓,同一波长下的透射率随粒径增大而增大;如图3(b)所示,模型的吸收率在0.3~2 μm波段范围内的变化也十分平缓,同一波长下的吸收率随粒径增大而减小。掺杂Ni粒子的薄膜模型的反射率几乎为0,不再讨论。
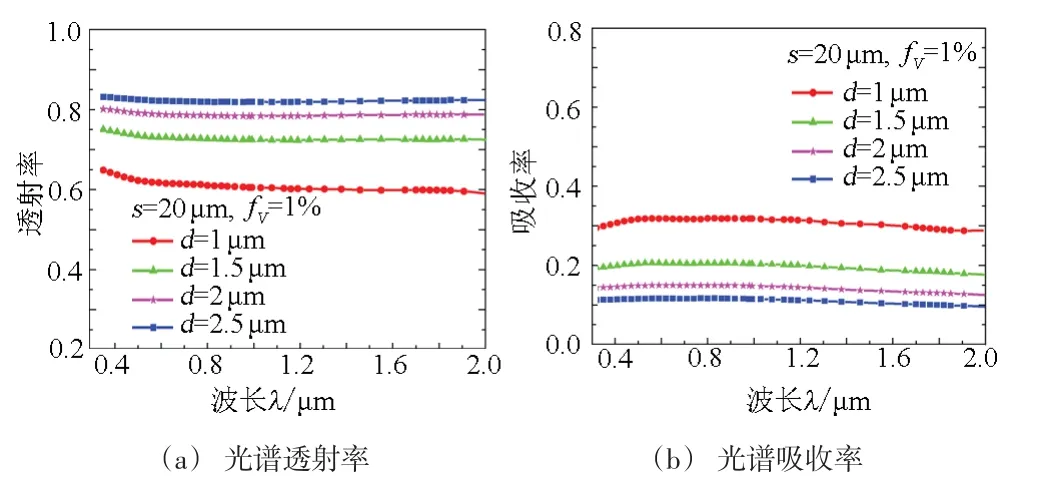
图3 不同Ni粒径下薄膜模型的光谱特性
2.1.2 Al2O3粒径
图4为掺杂Al2O3粒子的薄膜模型在0.4~0.8 μm波段范围内的透射率和反射率随粒径的变化规律。薄膜厚度s=100 μm,粒子的体积分数fV=10%。如图4(a)所示,当波长一定时,模型的透射率随粒径增大而增大;如图4(b)所示,当波长一定时,模型的反射率随粒径增大而减小。掺杂Al2O3粒子的薄膜模型的吸收率几乎为0,不再讨论。

图4 不同Al2O3粒径下薄膜模型的光谱特性
2.2 体积分数对光谱特性的影响
本节分别讨论了PDMS薄膜中掺杂Ni和Al2O3纳米粒子的体积分数对薄膜模型光谱特性的影响。
2.2.1 Ni粒子的体积分数
图5为掺杂Ni粒子的薄膜模型在0.3~2 μm波段范围内的透射率和吸收率随粒子浓度的变化规律。薄膜厚度s=20 μm,粒径d=1 μm。如图5(a)所示,薄膜模型的透射率随波长变化十分平缓,同一波长下的透射率随体积分数的增大而减小;如图5(b)所示,模型的吸收率随波长变化也十分平缓,同一波长下的吸收率随体积分数增大而增大。

图5 不同浓度Ni粒子的薄膜模型的光谱特性
2.2.2 Al2O3粒子的体积分数
图6所示为掺杂Al2O3粒子的薄膜模型在0.4~0.8 μm波段范围内的透射率和反射率随粒子浓度的变化规律。薄膜厚度s=100 μm,粒径d=1 μm。如图6(a)所示,当波长一定时,模型的透射率随粒子体积分数的增大而减小;如图6(b)所示,当波长一定时,模型的反射率随粒子体积分数的增大而增大。

图6 不同浓度Al2O3粒子的薄膜模型的光谱特性
2.3 膜厚对光谱特性的影响
本节分别讨论了掺杂Ni和Al2O3纳米粒子的薄膜厚度对模型光谱特性的影响。

图7 掺杂Ni粒子的薄膜模型的光谱特性随膜厚变化规律
2.3.1 掺杂Ni粒子的薄膜模型的厚度
图7所示为掺杂Ni粒子的薄膜模型在0.3~2 μm波段范围内的透射率和吸收率随膜厚的变化规律。粒径d=1 μm,粒子的体积分数fV=1%。如图7(a)所示,模型的透射率随波长变化十分平缓,同一波长下的透射率随膜厚的增大而减小;如图7(b)所示,模型的吸收率随波长变化也十分平缓,同一波长下的吸收率随膜厚的增大而增大。
2.3.2 掺杂Al2O3粒子的薄膜模型的厚度
图8所示为掺杂Al2O3粒子的薄膜模型在0.4~0.8 μm波段范围内的透射率和反射率随膜厚的变化规律。粒径d=1 μm,粒子的体积分数fV=10%。如图8(a)所示,当波长一定时,模型的透射率随膜厚的增大而减小;如图8(b)所示,当波长一定时,模型的反射率随膜厚的增大而增大。

图8 掺杂Al2O3粒子的薄膜模型的光谱特性随膜厚变化规律
3 结果验证
通过以上结果可发现:掺杂微纳米粒子的柔性薄膜模型的光谱特性受粒径影响。当波长不变时,掺杂Ni粒子的模型的吸收率与粒子浓度和膜厚成正比;掺杂Al2O3粒子的模型的反射率与粒子浓度和膜厚成正比;2种模型的透射率均与粒子浓度和膜厚成反比。下面依据布格尔定律[12]的表达式进行验证。
由布格尔定律得:

式中:τλ为光谱透射率;s和keλ分别为介质中射线的行程长度(薄膜厚度)和衰减系数。
keλ可以表示为:

式中:Ceλ为光谱衰减截面,且只与波长和粒径有关;N为粒子的数密度。
结合粒子的体积分数fV与数密度N之间的关系式,得:

光谱吸收率αλ、反射率rλ和透射率τλ之间的关系为:

由式(13)、(15)和(16)可得:上节得到的变化规律正确。
4 结束语
本文设计了一种在PDMS柔性透明材料中掺杂微纳米Ni或Al2O3粒子的薄膜模型,先利用米氏散射理论计算出单个粒子的辐射特性,再利用蒙特卡洛方法求解得到模型的辐射特性。研究发现,薄膜模型的光谱特性受粒径影响:当波长不变时,掺杂Ni粒子的模型的吸收率与粒子浓度和膜厚成正比;掺杂Al2O3粒子的模型的反射率与粒子浓度和膜厚成正比;2种模型的透射率均与粒子浓度和膜厚成反比。本文最后根据布格尔定律推出的关系式证明了光谱特性变化的机理。这种掺杂微纳米粒子的柔性薄膜结构,其光谱特性可以通过外界拉伸力进行可逆调控,故在军民事领域具有很大的应用潜能。

