基于神经网络模型的高铁轮对故障诊断和预测方法的研究*

季银银，刘婷婷，沈建洲，缪 响，张 颖

（1.南京工程学院信息与通信工程学院，南京 211167；2.南京工程学院工业中心，南京 211167）

0 引言

目前，铁路事业日益发展，客运高铁成为国内客运的主流客运方式之一，随着高铁快速发展，铁路旅客运输量的不断增长。截至2019年末，国家统计局发布高速铁路里程数据显示，2019年我国高铁总里程突破3.5万km，新增高铁运营里程超过5 000 km。纵观全球，我国高铁总里程全球占比超2/3，走在高铁建设项目的前列[1]。通过以上数据侧面反映出我国在高铁建设上具备雄厚实力。

在当今时代，高铁具有如下特征：（1）铁路非常平顺，采用无缝钢轨衔接，时速300 km以上的高速铁路采用的是无砟轨道；（2）铁路弯道少，弯道半径大；（3）发车密度大，车速快；（4）运行基本不受天气影响，适应性较强；（5）能很好地满足节能减排要求，属于绿色交通工具。基于以上特征，高铁的安全性能要求一定要高，影响高铁运营安全的主要因素有：人为因素、机器设备故障、环境因素、管理事故，这4个因素充分体现高铁安全的重要性。

高铁运行安全性尤为重要，其中高铁轮对的健康状况是高铁安全运行的重要保障，本文将重点研究高铁轮对的故障诊断。文献[1-2]中重点说明故障预测与健康管理技术可以在设备发生故障前对设备传输的相关信号进行故障预测，并可以利用这些信息进行维修和保障工作。通过故障预测与健康管理技术[3]在设备智能健康管理领域的研究，对故障诊断、检修、性能参数等数据进行全面的评估，预测出设备中的核心部件的可靠性与使用寿命，在历年研究中，故障预测与健康管理技术已经取得相关成果。而目前的故障诊断需要大量的数据去支持后台分析和诊断，这些数据中往往存在大量的干扰数据，因此，本文对高铁轮对运转时产生的振动特性、诊断方法、故障预测进行研究。研究高铁轮对核心部件受人为因素、机器设备故障、环境因素和管理事故这4个因素变化时的振动特性[4]，建立概率神经网络模型，对高铁轮对运转时传输的振动参数进行分析和诊断，从而迅速诊断出高铁轮对运转时产生的故障类型，再利用大量历史数据，分析各故障信号的特征，将故障数据样本输入到径向基网络模型中，快速预测出所上传故障信号的故障类型，控制中心可以第一时间采取措施，避免出现重大安全事故。

1 高铁轮对故障信号的特征提取与诊断

1.1 信号的特征选择

高铁轮对运转时会产生丰富的特征信息，包括声音信息、热力性能参数、振动参数等。选择合适的信号特征，并且这些特征要比较容易、准确地获得，更好地表示高铁轮对的工作状态，否则故障判断的性能和准确性都大打折扣。当高铁正常运行时，其瞬时转速波动信号可以反映高铁的工作状态。正常状态下，高铁轮对平稳运行，其声音信号、温度、振动信号等都在一定范围内平稳波动，且波动情况服从一定的分布[5-6]。当高铁轮对出现故障时，声音信号、温度曲线及振动信号灯都会产生严重的变形，可以作为故障诊断的依据[7]。

本文提出的方法采用高铁轮对运转时产生的振动信号作为样本，解析在轮对工作中，其能量参数、峰度参数、波形参数、裕度参数、脉冲参数和峰值参数[8]的变化，从而判断出轮对的工作状态。振动信号的分析包括时域和频域分析[9]，时域信号参数是振动波形的统计信息，包括均值、方差、均方值、峰度、裕度因子、脉冲因子等。由于时域信号分析具有更强的实时性，因此本文采用振动时域信号作为特征信号。

1.2 振动参数的提取

首先定义高铁轮对的5种故障类型分别为：轮对踏面损伤、轮对车轴裂纹、轮对轮辋裂损、辐板裂损故障、齿轮损伤，编号如表1所示。

表1 高铁轮对分类模式

采集到高铁轮对正常运转和5种故障模式下的振动信号，对振动信号做统计学处理，得到能量参数、峰度参数、波形参数、裕度参数、脉冲参数和峰值参数，形成1个六维向量。每种模式收集2份样本，共计12份训练样本。将时域计算代码输入到Matlab中，并运用参数运算的函数分析出上述振动参数。

设振动信号为{xi}，i=1～N，N 为采样数，则有：

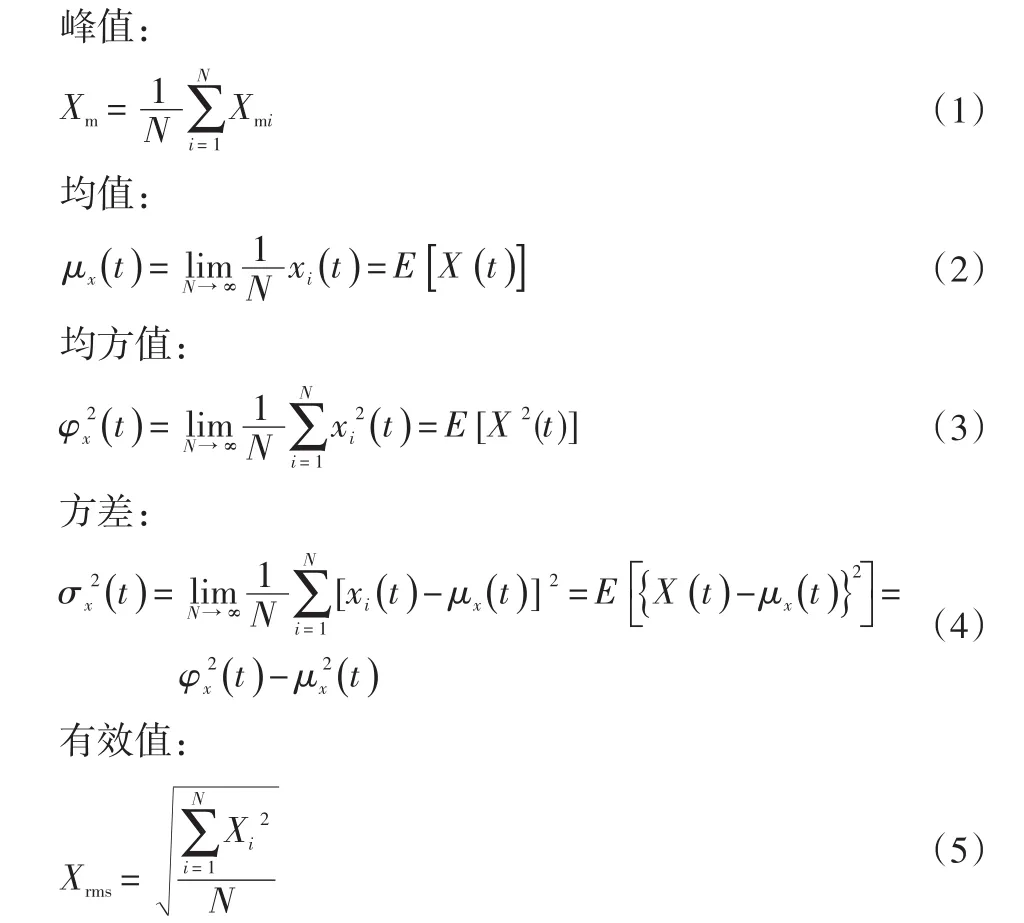
无故障的高铁轮对峰度值约为15，当高铁轮对峰度值大于16时，即表示轮对有一定程度的损伤。

波形参数：

裕度参数L:

高铁轮对中多级齿轮的振动信号往往包含有来自高速齿轮、低速齿轮以及轴承等部件的信息，在这种情况下，利用波形参数、裕度参数、脉冲指标来进行相关故障诊断。

峰值参数：

由于高铁轮对中踏面剥离、擦伤等一类故障，产生的脉冲波形总能量比较小，但波形的尖峰度很明显，因此，峰度参数适用于此类故障诊断。

1.3 概率神经网络建模

建立概率神经网络模型，将所采集的经过预处理后的高铁轮对的运转状态定义为X，X中包含的6种高铁轮对状态分别为：轮对踏面损伤X1、轮对车轴裂纹X2、轮对轮辋裂损X3、辐板裂损故障X4、齿轮损伤X5、正常状态X6。将振动信号设为变量A，对信号A预处理后提取出其中的能量参数A1、峰度参数A2、波形参数A3、裕度参数A4、脉冲参数A5和峰值参数A6。按照图1所示模型，编写算法。

图1 概率神经网络模型

对模型中隐含层输入求和后，比较出隐含层神经元的最大值，输出对应的类别序号。输出的序号即为诊断出的故障。

1.4 故障诊断实现

用六维向量表示高铁轮对的运转状态，对该向量处理、分类。故障诊断算法的流程图如图2所示。

图2 故障诊断算法流程图

该仿真实验中，采集高铁轮对正常运转和5种故障模式下的振动信号，对振动信号做统计学处理，得到能量参数、峰度参数、波形参数、裕度参数、脉冲参数和峰值参数。形成1个六维向量。每种模式收集2份样本，共计12份训练样本输入到概率神经网络模型中，得到表2所示仿真结果，由表中看出，概率神经网络所做的诊断完全正确。

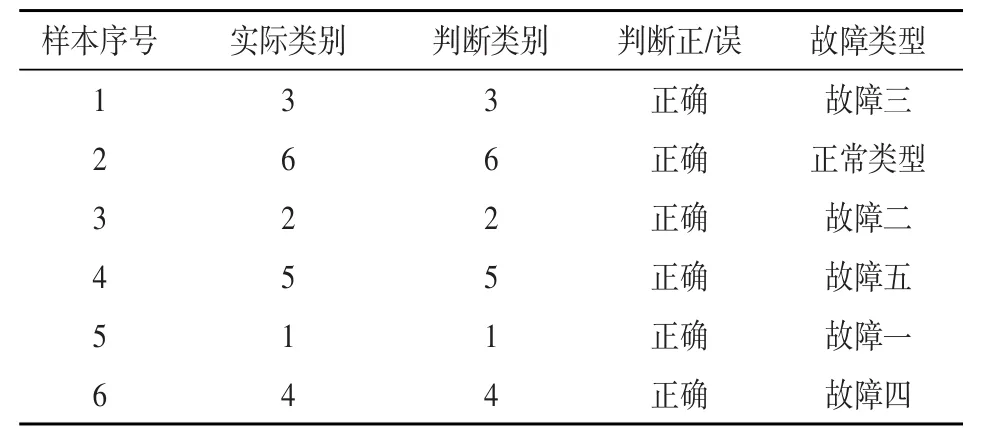
表2 故障诊断结果

图3 径向基网络结构图

2 高铁轮对故障预测

2.1 径向基网络建模

径向基网络模型有良好的模式分类和函数拟合能力，为3层前向网络。具体结构如图3所示。由于预测的输出值是高铁故障序号，根据上述内容介绍，所有的故障都已编号完毕，最终输出的结果是标量，故输出的神经元节点个数为1。隐含层的神经元根据第三章样本内容，一共有12个，输入层中神经节点一共有6个，分别为能量参数、峰度参数、波形参数、裕度参数、脉冲参数、峰值参数，形成如图4所示的函数关系：

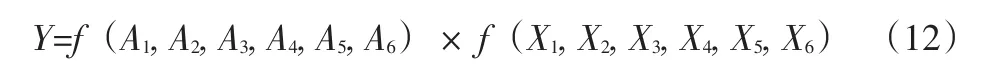
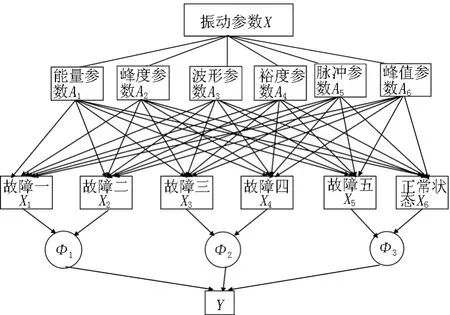
图4 径向基网络结构

A1～A6分别表示上述6个自变量，X1～X6为高铁轮对运转时的6个不同状态，Y为最终预测的故障结果，即该网络模型中，输入向量为：

隐含层的激活函数φi()x，i=1，2，3，…，为任一节点的基函数，选用格林函数。网络输出为Y。

2.2 故障预测方案

径向基网络创建完毕后，不需要训练可直接使用。输入样本中的振动参数首先与权值向量相乘，再输入到隐含层节点中，计算样本与节点中心的距离。该距离经过高斯函数映射后输出给输出层。本文中的故障预测样本与故障诊断的样本数据相同。

在上述过程中，需确定隐含层节点的中心及其标准差σ，以及隐含层与输出层之间的权值矩阵。

标准差公式为：

式中：D为样本与节点中心的距离；N为隐含节点个数。

一般来说，样本密集的地方可以适当增加节点中心，样本稀疏的地方可以减少样本中心，若节点是均匀分布的，中心节点也可以均匀分布。隐含层与输出层之间的矩阵可以通过求逆方式得到。

高斯函数：

利用径向基网络模型进行高铁轮对故障预测的算法流程图如图5所示。在高铁轮对故障预测算法中，设置误差容限为e-8，扩散因子为20，最大神经元个数为121。系统在调用函数时，会逐个增加神经元，使训练误差逐渐减小，指导误差小于容限。同时，在MATLAB命令窗口会显示实际添加的神经元节点的个数及训练误差值。如图6所示，命令窗口显示实际添加的神经元节点的个数及训练误差值，实际使用了50个神经元节点，训练误差值为10-4量级。

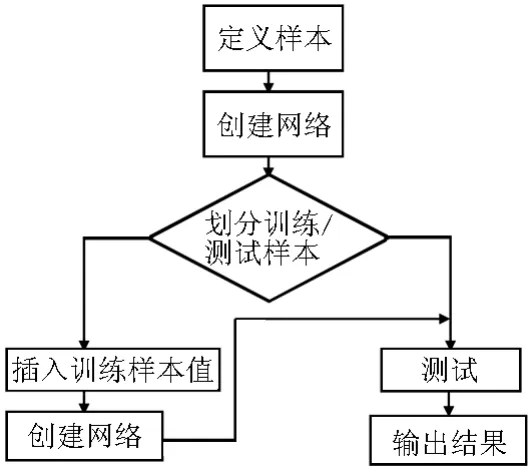
图5 高铁轮对故障预测步骤

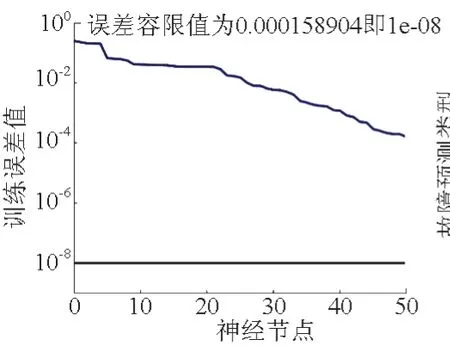
图6 误差下降曲线

图7 预测值与真实值对比图

综上所述，基于径向基神经网络模型的高铁轮对故障预测系统，首先需要经过采集大量历史数据，将历史样本数据进行分类；其次，将历史数据输入到径向基网络模型的算法中，经分类、创建神经元、测试等流程的重复后，最终输出所预测的故障类型，并输出故障预测与高铁轮对正常状态的比较值，得到最终结果。该过程中，神经元的数量需要限制在固定值内，否则将导致重复工作以致程序混乱的结果。

实际高铁轮对故障与预测故障结果如图7所示。由图中可以明显地看出，预测值与真实值很接近，且预测值与真实值的变化趋势基本一致。该算法结果从相对误差的角度来说，测试样本的平均相对误差为5%，最大相对误差接近7%，因此，可以得出结论，径向基网络可以准确地预测出高铁轮对的故障，其对于故障的预测值是真实可靠的。

3 结束语

本文对高铁轮对的故障诊断方法进行研究，为高铁轮对运行时产生的故障提供了诊断方法。利用概率神经网络模型进行轮对故障诊断，精确分析出高铁轮对运行时所上传的故障信号中的故障信息，通过从时域振动信号中提取出能量参数、峰度参数、波形参数、裕度参数、脉冲参数和峰值参数，输入到网络模型中，这个过程可以精确诊断出高铁轮对发生的故障，及时准确地解决问题，使轮对安全可靠地运行。

为了大大降低高铁轮对发生安全事故的概率，在该研究中，引入了利用径向基网络模型进行高铁轮对故障预测的方法，在大量历史数据中，提取各类故障信息，确定具有代表性的节点中心，接着在高铁轮对运行时的能量参数、峰度参数、波形参数、裕度参数、脉冲参数和峰值参数输入到径向基网络模型中，算法在进行分类、训练、测试过程后，在短时间内确定离节点中心最接近的故障类型，并输出故障预测曲线，根据所得结果，故障预测值与高铁轮对正常状态变化值趋势一致，故径向基网络模型的预测值是可靠的。

该研究可以为高铁轮对故障诊断和故障测试技术提供参考，在较短时间内，高铁控制台可以较早发现轮对异常情况，第一时间确定轮对故障类型，及时进行检修，降低事故发生风险。