基于递归神经网络的多机器人智能协同控制*

程韬波，李晓晓 ，徐智浩，周雪峰

（1.广东省智能制造研究所，广州 501070；2.广东省现代控制技术重点实验室，广州 501070）

0 引言

机器人被誉为“制造业皇冠顶端的明珠”，是实现智能制造的重要载体[1]。近年来，随着机器人技术的推广应用，其操作要求越来越复杂化、精密化，单个机器人难以满足当前柔性化生产的市场需求，主要表现在[2]：（1）单机器人负载能力有限、工作空间较小，难以适应大空间加工任务；（2）单机器人加工的作业效率有限；（3）单个机器人的自由度有限，难以满足实现复杂度高的加工任务。多机器人协作系统具有高冗余自由度、结构灵活多变等特点，是解决上述问题的有效途径之一。其中，多机协同控制指通过设计协同控制策略，使多机器人执行共同的任务，在多机搬运、装配、焊接等领域应用广泛[3-5]。

针对快速切换的加工任务，传统示教或离线编程方式效率不足；实时运动控制工程意义较强，但同样面临技术挑战：需要根据多机器人加工任务实时设计控制量，实现对给定任务轨迹的跟踪，同时能够实时避免机器人超越其关节约束。此外，区别于传统单机控制，多机器人系统之间可能存在结构闭链，机器人之间的相互影响对系统的同步性有很高的要求。

针对上述挑战，金龙等[6]利用递归神经网络（RNN）的实时处理性能为双机器人提出一种基于RNN的同步控制方案，但未提及机器人之间的通信方式。李帅等[7]提出一种树形结构通信的多机器人协同控制方法，之后他们从博弈论的角度再次探讨了该问题，提出一种分布式协同控制方案[8]。张海涛等[9]为实现机器人圆形编队提出一种多机器人系统控制算法，通过使用排斥力/转向力和相位调节机制，避免机器人之间或机器人与墙壁的碰撞。查延麟[10]结合量化通信和区间算术方法提出一种考虑系统不确定性的多移动机器人协调控制策略。陈梅等[11]提出一种队形轨迹跟踪控制方法，可使各机器人较快形成期望队形，以期望队形追踪期望轨迹。Alessandro[12]提出一种分布式自适应控制策略，在机器人未知系统完整状态的情况下实现协同控制。

上述多机器人协同控制策略大多基于系统状态信息全局未知的情况，在设计控制方案时需要考虑期望轨迹信息获取等因素。受益于5G通讯技术的发展，使得多机协同控制过程中可实时获取各机器人的状态信息，保证了集中式控制策略在工业多机器人的系统实现。机器人跟踪控制问题通常分为两类：关节空间跟踪和任务空间跟踪。关节空间跟踪目标是设计一个控制器控制机器人的每一个关节去追踪一条预定轨迹。任务空间跟踪是在笛卡尔空间建立期望轨迹，将控制命令发送给关节的每个驱动器，然后控制末端执行器在笛卡尔空间执行。由于笛卡尔空间和关节空间之间映射关系的高度非线性，任务空间跟踪比关节空间跟踪更困难。

本文研究关节约束下多机器人任务空间跟踪的智能协同控制问题，以轨迹追踪为主要任务，首先构建同步跟踪误差并设计外环控制策略，选取关节速度范数最小化为次级任务，进一步考虑关节速度和关节角限幅，将多机协同运动控制问题建模为一个二次型优化问题，然后设计一个动态神经网络控制器实时求解控制量，最后建立MATLAB与V-REP联合仿真实验平台以验证多机协同控制策略的有效性。

1 问题描述

1.1 机器人模型

机器人的正向运动学模型可以描述为：

式中：r(t)∈ℝn，为机械臂末端执行器t时刻在笛卡尔空间中位置和方向的n维向量；θ(t)∈ℝm，为关节空间中的m维向量，它的每一个元素表示一个关节角，不失一般性，本文考虑机器人存在冗余自由度的情况，即m＞n；f(·)为笛卡尔空间到关节空间映射关系的非线性函数，通常由机械臂的结构和参数决定。

对式 （1）求导可得速度层r˙(t)与 θ˙(t)的映射关系：

式 中 ： J(θ(t))=∂f(θ(t))/∂θ(t)∈ℝm×n， 为 雅 可 比 矩 阵 ；r˙(t)和θ˙(t)分别为机械臂末端执行器的笛卡尔速度与关节角速度。

由于f(·)的非线性和冗余性，给定期望轨迹r(t)→rd(t)很难获得相应的关节角θ(t)。式（2）速度层从关节空间到笛卡尔空间的映射简化了该问题。

1.2 控制目标

本文研究多机器人任务空间跟踪的智能协同控制问题，考虑机械臂关节角和关节速度限幅，定义第i个机械臂的关节角 θi和角速度的上下界分别为，期望轨迹为rd(t)，各机器人相对其初始位置的位移为ri(t)-ri(0)，i=1,2,…,N。智能协同控制的目标可以描述为：设计关节速度指令使机器人协同完成轨迹追踪任务且不发生相对位移，即r1(t)-r1(0)=…=rN(t)-rN(0)=rd(t)-rd(0)。

2 协同控制器设计

2.1 二次型问题描述

机器人逆运动学指给定笛卡尔空间期望速度r˙(t)和机器人模型雅可比矩阵J(·)已知情况下计算机器人对应位置的关节速度θ˙(t)。伪逆法求解机器人逆运动学相对简单，然而该方案未考虑机器人关节约束。由于机器人的物理结构和机械臂关节通常由一个伺服电机驱动，关节旋转角度和关节角速度有限。如果违反关节限幅，机器人协同追踪将会产生大追踪误差或造成对机械臂的损害甚至是协同追踪任务失败。由于m＞n，冗余机械臂的逆运动学解不唯一，机械臂冗余的性质可以使得根据某些特定的优化标准（如关节速度范数最小化、重复性优化、关节加速度范数最小化等）和约束条件（关节角、关节速度或关节加速度约束）在所有可行解中选择最优的一个。

基于约束优化思想，将机械臂的物理约束抽象为不等式约束，机械臂末端执行器笛卡尔空间到关节空间的非线性映射抽象为等式约束，优化目标函数选择关节速度范数最小化，将多机器人协同运动控制问题建模为一个二次型问题如下：

为提高机器人之间的同步精度，设计一个同步机制并将式（4）改写为：

如果期望机器人末端执行器以速度r˙i运动，式（4）描述了机器人关节角速度θ˙i需要满足的条件，同时也是系统协同跟踪误差收敛到零的充分必要条件。由于约束式（5）和式（6）描述在不同层，很难直接求解该二次型问题。因此利用速度逃逸法[13]将式（5）和式（6）共同描述在速度层，得到：

2.2 RNN控制器

对于上述得到的速度范数最小化约束优化问题，定义拉格朗日函数为：

式中： NΩi(θ˙i)为集合 Ωi在 θ˙i处的正规锥。

式（12）可以进一步描述为：

式中：PΩi为投影算子。

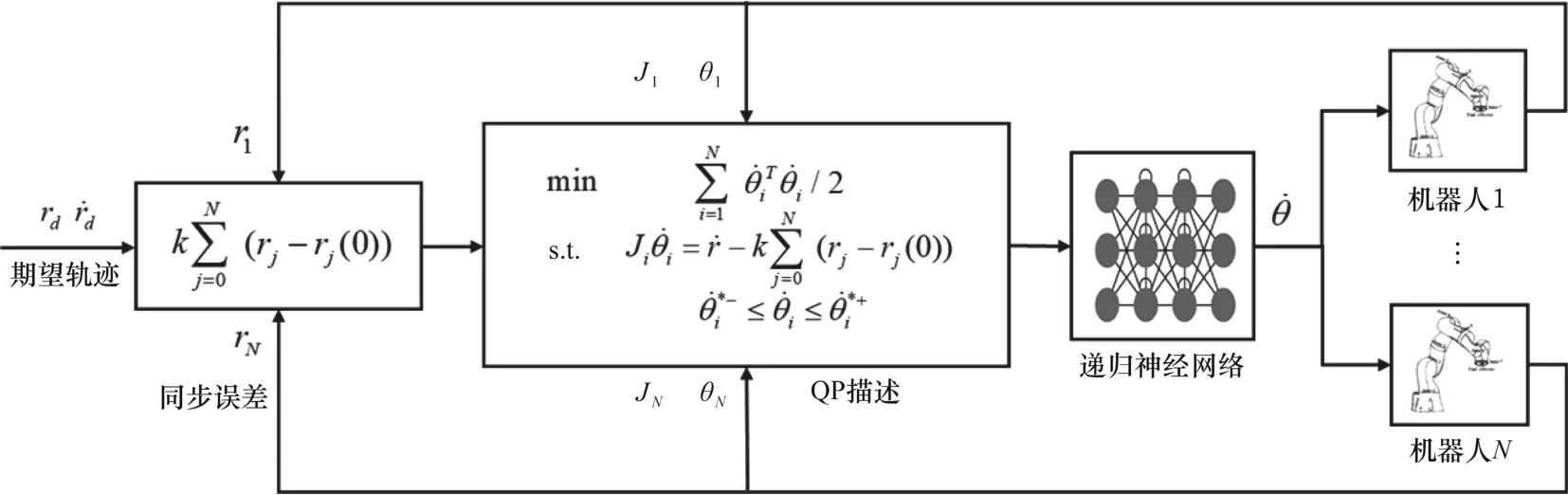
图1 基于RNN的多机器人协同控制框图

由于多机器人系统的非线性性质，式（8）具有高度非线性的特点，目前尚没有可以直接求解式（8）的解析方法，而且利用数值算法求解的效率很低且功能有限，利用RNN并行计算性能优化的特点，本文设计了RNN神经动态求解器求解：

式中：ε＞0为正常数。

基于RNN的多机器人智能协同控制框图如图1所示。

综上所述，基于RNN的多机器人系统协同控制问题可归纳为三步：（1）建立同步误差，选择优化目标函数并将机械臂协同控制问题建模为约束二次型优化问题（见式（8）～（10））；（2）在对偶空间中研究该问题，以非线性方程的形式建立其解表达式（见式（16）～（17））；（3）设计一个收敛的神经动力学系统，其稳态解与非线性方程组的稳态解相同（见式（16）～（17））。

3 仿真实验

为验证所提协同控制方案的有效性，本文建立了MATLAB+V-REP[14]联合仿真实验平台。以图2所示的7自由度iiwa R800机械臂为对象，机器人个数为3，期望运动轨迹设定为三环路径：

式中： μ=πt/T，实验设置中T=10；参数lx，ly和lz分别设置为-0.191 5，0.511 0和0.656 0。神经网络参数ε1=…=ε3=0.000 5。3个机器人的关节角初始值θ（0）分别设置为[0 , 20,0,-60,0,30,0]T·π/180°rad ，[0,20,0,-60,0,30,0]T·π/180°rad， [0,-20,0,60,0,-30,0]T·π/180°rad 。控制增益参数设置为k=1，α=8。关节角和关节速度的上下限分别为=-1.5 ，-0.7。仿真实验中本文仅考虑了3D空间中的位置控制，表1所示为iiwa R800机械臂的DH参数。

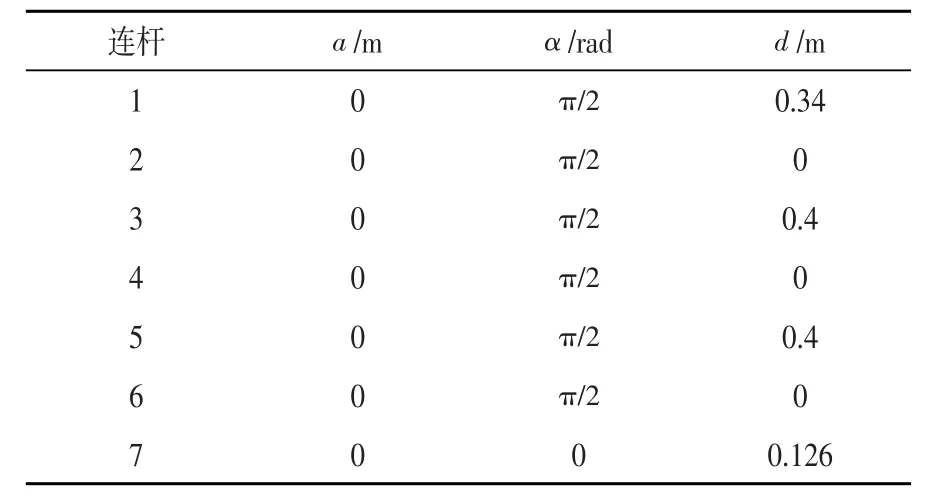
表1 DH参数表

图2 7自由度iiwa R800机械臂模型

图3 对三环曲线的协同控制结果

实验结果如图3、4所示。图3（a）所示为轨迹误差曲线，末端执行器位置误差通过计算e=r-rd∈ℝ3获得，基于所设计的控制器，机器人实现的轨迹与期望轨迹之间的误差可达到10-4量级。图3（b）～（d）分别为λ，关节角θ和关节速度的曲线图。在t=8时关节速度θ达到了最大值（±1.3 rad），在t=1和t=5时关节速度达到了最大值（±0.4 rad/s），但是关节角和关节速度皆在所设置的约束范围之内，并且在协同控制方案的控制下，曲线都比较平滑，处于一个相对平稳的状态。图4（a）所示为三环曲线跟踪过程中V-REP环境下截取的跟踪效果，图4（b）所示为最终状态下机器人实现的曲线跟踪结果，可以看到在神经网络协同控制器控制下所有机器人最终都精确实现了期望的三环路径轨迹。

图4 V-REP环境下对三环曲线的跟踪效果

4 结束语

本文针对多机械臂协同运动控制问题提出了一种基于RNN的协同控制方案。机器人关节角和关节角速度限幅描述为不等式约束，设计了一个动态RNN控制器实时控制机器人的运动。MATLAB与V-REP联合仿真实验验证了在神经网络协同控制策略的控制下，多机器人系统成功地实现了期望轨迹跟踪，跟踪误差可达到10-4量级，且关节角和关节速度值都在所设置的限幅内。

对多机器人系统而言，障碍物避免方案不仅要考虑机器人与环境的碰撞，还要考虑机器人之间的碰撞，这是一个值得探讨且充满挑战的问题。未来工作将致力于多机器人系统障碍物避免策略研究。