基于AHP与正则化RBF的多响应稳健参数优化

黄鸿琦

(河南工学院 管理学院，河南 新乡 453003)

一、引 言

20世纪60年代以来，通过生产工艺技术的不断改进，金属化薄膜电容器实现小型化，推动其应用领域的不断发展。进入21世纪以来，随着高科技技术的不断提升，航天、通讯、汽车、计算机等领域整机产品需要金属化薄膜电容器具有更高的稳健性、可靠性、安全性。

金属化薄膜电容器具有体积小、容量大、耐热耐湿的特点，且金属化薄膜介质局部击穿后能够立即恢复到击穿前的电性能，使得电容器具备自愈功能[1]，应用广泛。但在使用过程中金属化薄膜电容器的稳定性较差，且发热引起的电容器损耗加速电容器老化[2]，严重时发生爆炸或燃烧。电容器损耗的特性参数是损耗角正切[3]，损耗角正切值越小，损耗越小，电容器性能越好，寿命越长。热聚合工艺是影响电容器电容量及损耗角正切值的关键工序，若热聚合不充分将会导致容量下降，损耗角正切值增大。为满足客户多重需求，金属化薄膜电容器的改善需要考虑多个质量特性及其稳健性。基于上述分析，对热聚合工艺多个质量特性改善中需要着重考虑质量的稳健性及损耗角正切值的改善。

多响应稳健优化设计是质量工程领域的难点与热点问题。目前，多响应参数优化方法的主要思想是将多响应降维转化为单响应。层次分析法(AHP，analytic hierarchy process)是一种通过定性与定量相结合解决多目标复杂问题的决策评价方法[4]，李强[5]利用层次分析法——模糊综合评判的方法对齿轮制造流程的工艺参数优化优先等级评判及排序，提出对重要工艺参数改进的方案。将其思想运用到多响应参数稳健优化方法中，使得综合决策评价结果倾向于重点改善指标，计算简便，便于企业运用与掌握。最后，通过构建因子与综合决策评价间的模型搜索综合决策评价最优的因子参数组合点。但随着生产工艺复杂程度的提升，多响应参数优化存在复杂多响应问题，使得真实参数数据间的机理关系难以掌握。目前，主要利用支持向量机[6]、ANFIS(adaptive neuro- fuzzy inference system)[7]、神经网络[8-10]、遗传算法[9-11]等智能算法建立模型全局搜索最优组合。RBF神经网络[12]是一种常见的神经网络方法，其训练速度快，学习及泛化能力强。严格RBF神经网络是一种神经元的个数与输入值个数相等的RBF神经网络，因此，在参数设置、训练速度等方面具有更优的表现，易于操作和评价，且通过对离散的试验数据学习可构建连续空间模型，优化结果能够达到全局最优。由于网络模型可能存在超拟或欠拟现象，构建能否较为真实地反映变量间实际映射机理结构难以通过误差判断，因此，给出主效应与神经网络模型的对比，评价网络模型构建的有效性。最后，在所构建的严格RBF神经网络模型中搜索最优参数组合点，即为按质量改善要求所得的全局最优参数组合点。

二、层次分析法

AHP是一种常见的多目标决策方法，将复杂的多目标决策问题作为一个整体系统，通过定量与定性分析结合，利用决策者的经验判断各衡量目标之间相对重要程度，以权数给出反映因素的重要程度次序。多响应参数稳健优化是一种多质量特性权衡整体最优的多目标优化，将AHP思想运用其中，根据质量改善的目的构造判断矩阵，通过定性指标模糊量化方法得到各响应均值和标准差(评价响应稳健性)的评判权重。即主要利用AHP思想建立各响应均值和标准差的单层次模型，以权重分配作为改善指标的主次依据。

(一)构造判断矩阵

构建判断矩阵A需要利用表1中九分位比例标尺，其中ai、aj表示因素，aij表示ai对aj的相对重要性数值，本文需要对6个指标因素进行优化，i、j=1, 2, 3, 4, 5, 6。

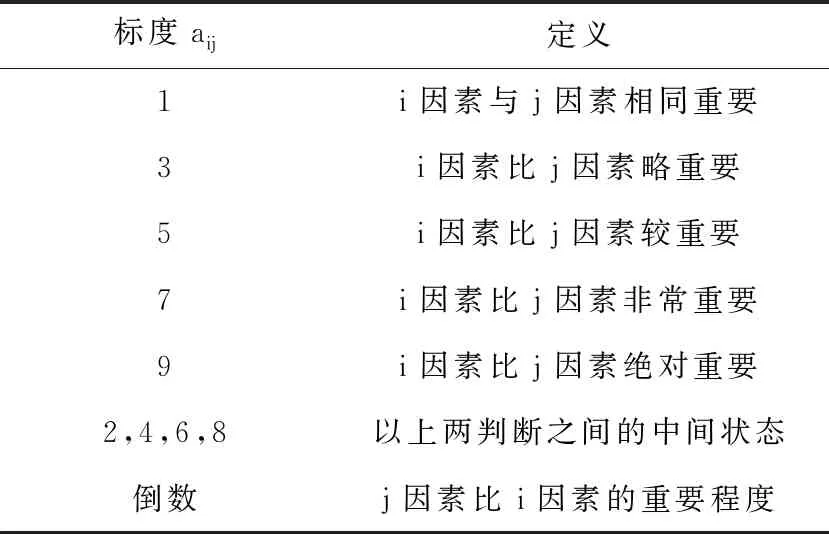
表1 九分位比例标尺

(二)层次单排序权重计算

根据上文中判断矩阵，采用公式AW=λmaxW，求判断矩阵A的最大特征值λmax及所对应的特征向量W，并对向量W做归一化处理，得到权重分配。

(三)一致性检验

为检验各因素重要度之间的协调性，需要对判断矩阵进行一致性检验。

检验公式为:

式中：CR为判断矩阵的随机一致性比率；CI为判断矩阵的一般一致性指标；RI为判断矩阵的平均一致性指标；n为指标的个数，n=6时，RI=1.26。当判断矩阵A的CR<0.1时，认为A具有满意的一致性，否则需要调整矩阵中的元素，使其满足一致性检验。

三、正则化径向基神经网络

RBF神经网络是一种常见的、高效的前馈式神经网络，其结构简单，学习速度快，在构建复杂系统模型中，模型构建的曲面平滑，能够较为真实地反映实际映射关系。正则化RBF网络是RBF神经网络的一种网络模型，具有最佳逼近性能，是一个通用逼近器，其拓扑结构结构如图1所示，包括输入层、隐层和输出层。

输入层中，X=[x1, x2,..., xn]T为输入向量，输入层的输入节点数目等于输入向量X的维数。隐层中，隐层节点数P等于输入层的输入样本数，是正则化网络特点，φ(X, Xj)(j=1,2,…,P)为任一隐节点的激活函数，一般选用Gauss函数。输出层Z=[z1, z2,..., zt]T为网络输出，节点数为1，采用的线性激活函数是由所有的隐层单元相连输出的线性加权和。

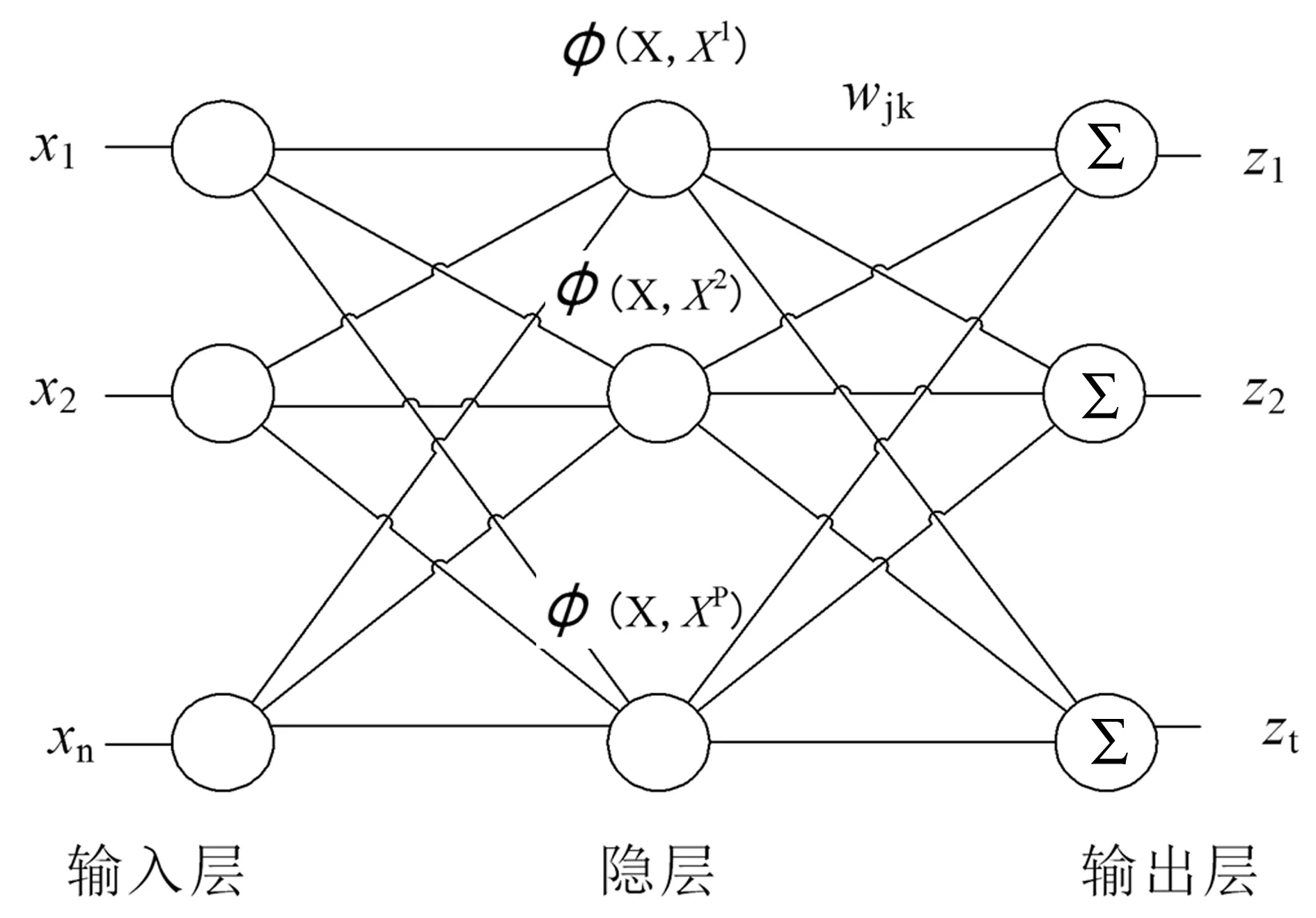
图1 正则化RBF神经网络拓扑结构

四、热聚合工艺多响应稳健参数优化

(一)试验数据

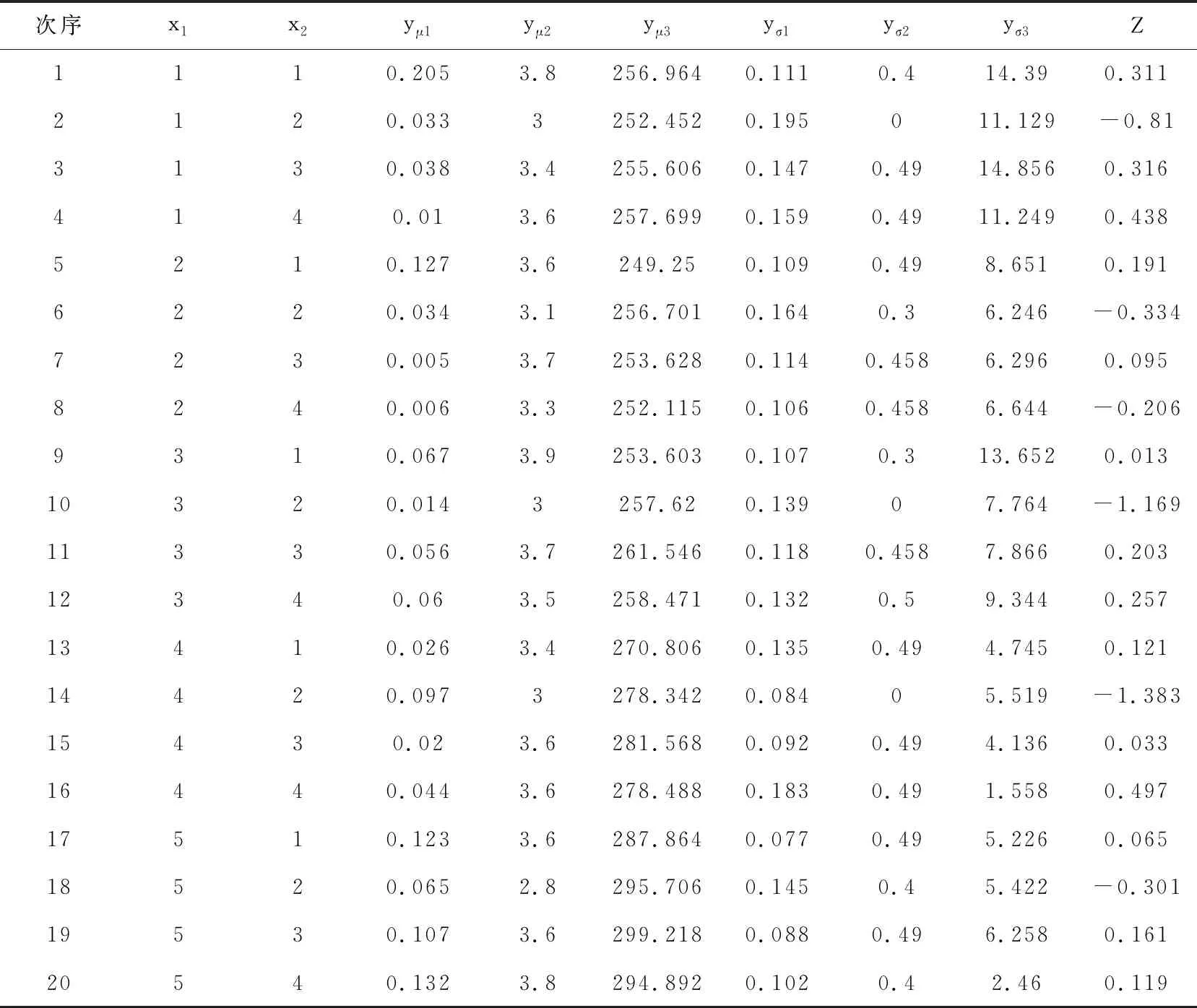
表2 试验数据

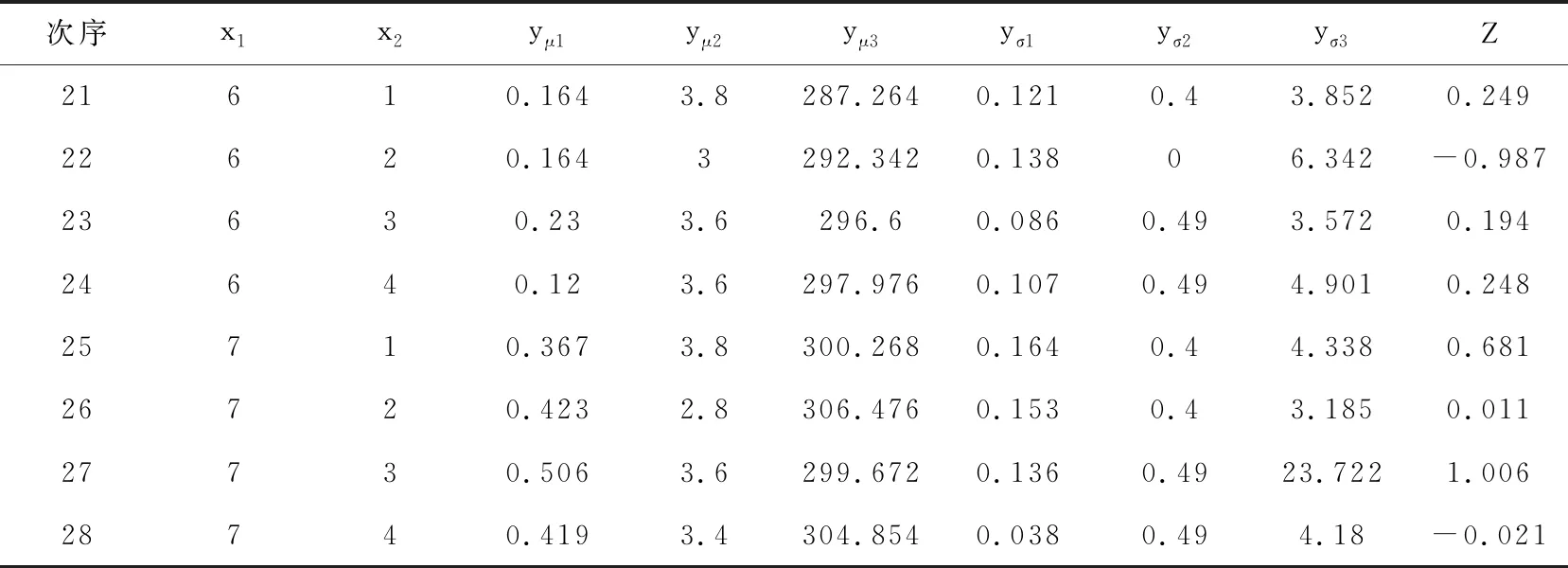
续表2 试验数据

研究铝金属聚丙烯薄膜PPM/A电容器高温定型工艺参数优化，针对电容器热聚合工艺质量特性的影响因素以及性能参数进行试验设计，设定电容器的热聚合温度(记为x1)在7个水平分别为95℃、100℃、105℃、110℃、115℃、120℃、125℃，电容器的聚合时间(记为x2)在4个水平分别为4小时、6小时、8小时、10小时，各水平组合中温度设置在1、2、3水平组重复实验10次，温度设置在4、5、6、7水平组重复实验5次。热聚合后温度冷却到85℃时测量电容器的三个响应值：容值(y1)、损耗角正切值(y2)以及温度系数(y3)，分别为望目特征(目标值为45.45μF)、望小特征、望小特征。容值与目标值之差的绝对值调整为望小特性，使得三响应均为望小特性。如表2所示，yμ1，yμ2，yμ3为重复实验的响应均值，yσ1，yσ2，yσ3为重复实验的响应标准差，标准化处理后分别用Yμ1，Yμ2，Yμ3，Yσ1，Yσ2，Yσ3表示。

(二)基于AHP的综合评价指标计算

(1)分析主次改善指标。根据金属聚丙烯薄膜电容器的质量改善需求，根据电容器的热聚合工艺中温度和时间优化电容器容值、损耗角正切值以及温度系数。通过质量改善分析，在改善中需要着重优化各质量特性的稳健性及损耗角正切值。

(2)建立判断矩阵。利用九分位的比例标度对热聚合工艺中电容器容值、损耗角正切值以及温度系数的均值与标准差确定权重评判矩阵，如表3所示。

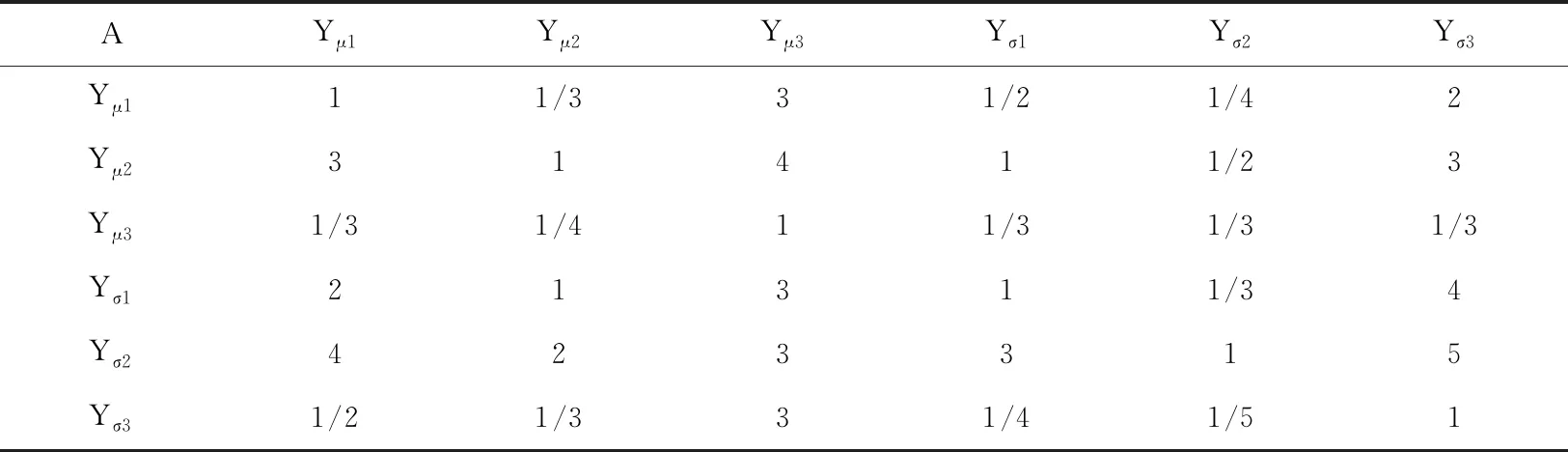
表3 判断矩阵

(3)求判断矩阵的权重向量及最大特征值归一化后权重向量为W=[0.1063，0.2111，0.0552，0.1882，0.3633，0.0759]，λmax=6.3871。

(4)一致性检验。计算一致性指标CI=0.0774；计算一致性比例CR=0.0614<0.1，即矩阵满足一致性。

(5)将排序权值向量W分别作为Yμ1，Yμ2，Yμ3，Yσ1，Yσ2，Yσ3的系数，计算得到综合评价指标Z(如表1所示)，由于Yμ1，Yμ2，Yμ3，Yσ1，Yσ2，Yσ3均为望小，因此找出使得Z值最小的水平组合即为最优参数组合。

利用Minitab软件，将Z作为响应，x1和 x2作为因子构造主效应图，如图2所示，横轴表示x1、x2因子水平，纵轴表示在各因子水平下响应Z值的平均值。由主效应图得到x1在3和4水平， x2在2水平时，以判断矩阵为评判依据的各指标相对重要程度优化综合评价指标Z值平均值最小。但离散的参数水平可能未达到全局最优，利用神经网络的方法建立映射模型搜索全局最优点。

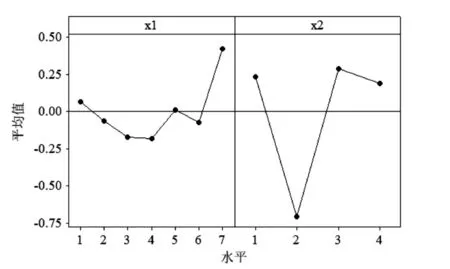
图2 主效应图

(三)基于正则化RBF神经网络的全局优化

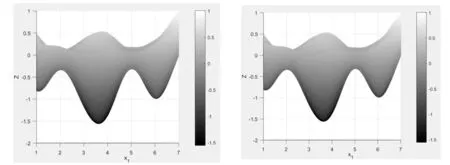
图3 x1、x2与Z的映射模型 图4 侧视图Z-x1

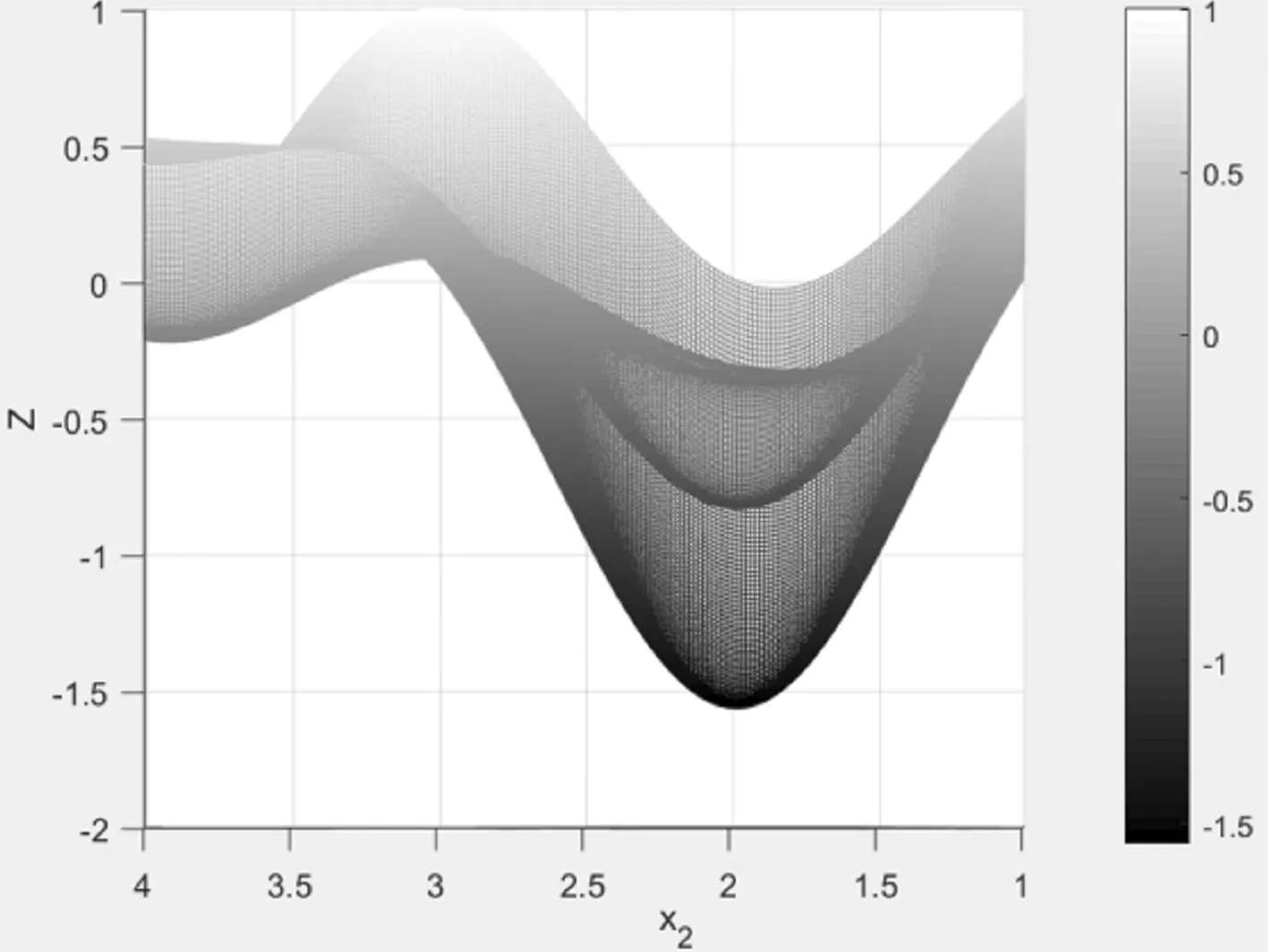
图5 侧视图Z-x2

在Matlab软件中创建语句为net = newrbe(P , T , Spread) ，以水平组合[x1x2]作为输入向量P，以综合评价指标[Z]作为输出向量T，设置径向基的扩展速度Spread为0.8。构建模型如图3所示，训练达到误差平方和为1.3106e-31，学习能力良好。通过空间映射模型的旋转分别得到Z值与x1、x2的侧视图4与图5，并将其与图2主效应图对比，能够较为准确地反映x1、x2与最小Z值的关系，因此，正则化RBF神经网络构建的映射模型良好。搜索得到最优点为(x1x2)=(3.61 1.99)，即当热聚合温度和时间设置为108.05℃、5.98小时，使得Z值最小为-1.56。

针对铝金属聚丙烯薄膜PPM/A电容器高温定型工艺参数优化中容值、损耗角正切值以及温度系数，根据改善需要着重优化各质量特性的稳健性及损耗角正切值。利用AHP的定性定量分析给出各响应指标满足一致性检验的优先优化权重，使得综合评价指标优先考虑响应稳健性及损耗角正切。为达到全局优化效果，利用正则化RBF神经网络建立因子与综合评价指标的网络模型。为避免超拟或欠拟，与效应值进行对比，判断模型构建的良好性，在全局范围内找出最优参数组合。