环R+uR+vR+uvR 上线性码的MacWilliams 恒等式

王艳萍，王喜喜，王 艳

自Shannon［1］初次提出了编码知识与信息论之后，广大学者便在此方向上进行了大量的研究.在文献［2-5］中，学者研究了在Z4、Zk、Galois 环上的一些重量计数器所对应的MacWilliams 恒等式；文献［6-9］讨论了Mac-Williams 恒等式，不同环上的重量分布.

本文给出了环R+uR+vR+uvR(u2=u,v2=v,uv=vu) 的定义，讨论了在此环上码的不同重量计数器，最后探究了环上线性码和它们的对偶码各种分布所对应的MacWilliams恒等式.此研究可为纠错码理论提供丰富的理论依据.

1 准备知识

记 ℜ=R+uR+vR+uvR={a+ub+vc+uvd|a,b,c,d∈R} ，此时u2=u,v2=v,uv=vu.令的特征p是奇数.环R以＜λ＞为极大理想，且是有限链环，则知ℜ 不是有限链环.设α1=1-u-v+uv,α2=uv,α3=u-uv,α4=v-uv，则 有(i≠j)，进而得ℜ ≅α1R⊕α2R⊕α3R⊕α4R，所以对∀r∈ℜ ，可 唯 一 写 成r=α1x+α2y+α3z+

设∀X,Y∈ℜn，X=(x0,x1,…,xn-1) ，Y=(y0,y1, …,yn-1) ，其 内 积 为X⋅Y=x0y0+x1y1+…+xn-1yn-1.如果X⋅Y=0 ，则X,Y正交.线性码C是环ℜn上的，则C的对偶码C⊥={x|x⋅y=0,∀y∈C} ，如果C=C⊥，则C是自对偶码.

定 义C1={x∈Rn|∃y,z,t∈Rn,α1x+α2y+α3z+α4t∈C} ，C2={y∈Rn|∃x,z,t∈Rn,α1x+α2y+α3z+α4t∈C} ，C3={z∈Rn|∃x,y,t∈Rn,α1x+α2y+α3z+α4t∈C} ，C4={t∈Rn|∃x,y,z∈Rn,α1x+α2y+α3z+α4t∈C} ，则Ci(i=1,2,3,4)是R 上长n的线性码；C=α1C1+α2C2+α3C3+α4C4，此表示唯一.

定义φ:ℜ →R4，有φ(r)=(x,y,z,t) ，且有wL(r)=wH(x,y,z,t). 将 其 扩 展 为 Φ ：ℜn→R4n，∀c=(c0,c1,…,cn-1)∈ℜn,ci=α1xi+α2yi+α3zi+α4ti，有Φ(c)=(x0,x1,…,xn-1,y0,y1,…,yn-1,z0,z1,…,zn-1,t0,t1,…,tn-1)∈R4n，

注1：①记wi(c) 为c中wL(c)=i(0 ≤i≤4)的元素成分个数.②∀x,y∈ℜn，记dL(x,y)=wL(x-y)，从而推出Φ 为同构映射，且保距.

引理1［10］环ℜ 上的线性码C，则有

（1）C⊥为ℜ 上的线性码；

（2）Φ(C)=C1⊗C2⊗C3⊗C4,|C|=

（3）Φ(C⊥)=Φ(C)⊥=C1⊥⊗C2⊥⊗C3⊥⊗C4⊥,

2 线性码的MacWilliams 恒等式

C的Lee 重量分布为{B0,B1,…,B4n} ，其中Bi为Lee 重量是i的码字的个数，0 ≤i≤4n.C⊥的Lee 重量分布为的Lee 重量计数器为则有的广义对称重量计数器为重量计 数 器 为

设ℜ={g1,g2,…,gq4l}，其中则且中的每一个元素都需按照一定顺序排列，并且两两不同.∀gi∈ℜn，记I(i)=wL(gi) ，其中记g1=0. ∀c=(c0,c1,…,cn-1)∈ℜn，ni(c)：c中值是gi的元素成分个数，0 ≤i≤q4l，则有C的完全重量计数器

定理1C是ℜ 上长为n的线性码，则（1）LeeC(X,Y)=SweC(X4,X3Y,X2Y2,XY3,Y4)；（2）SweC(X0,X1,X2,X3,X4)=CweC(XI(1),XI(2),…,XI(q4l))；

（3）HamC(X,Y)=SweC(X,Y,Y,Y,Y)；

（4）LeeC(X,Y)=HamΦ(C)(X,Y)；

（5）HamC(X,Y)=CweC(X,Y,…,Y).

注2：定理1可用文献［10］的方法类似证明.

下 面 引 入 变 量ξ1,ξ2,ξ3,ξ4，满 足，可唯一表示为是R＜λ＞的一个本原元，则对∀c∈ℜ

ℜ 上的复值映射θc：∀c′∈ℜ 有

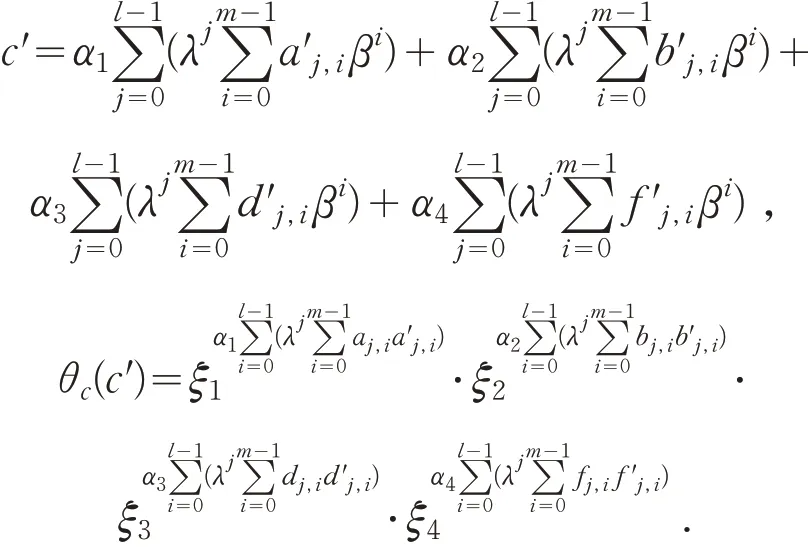
注 3：① 当c=1 时 ，有θ1(c′)=②∀c′,c″∈ℜ ，有θ1(c′+c″)=θ1(c′)θ1(c″).③上述扩展到ℜn，有

引 理2［10］∀c∈ℜ 和 任 一 非 零 的 理 想I∈ℜ ，有

定理2 对环ℜ 上的码C，有

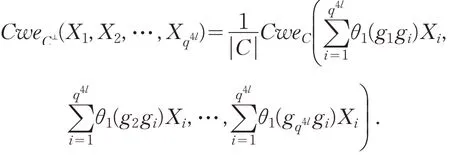
证 明 对∀c∈C，有

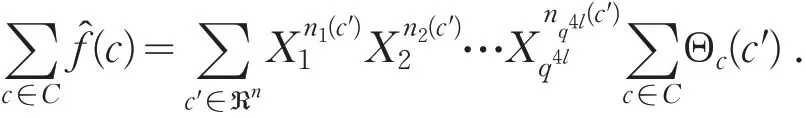
固定c′∈ℜn.

（1）如 果c′∈C⊥，则Θc(c′)=θ1(0)=1 ⇒

（2）如果c′∉C⊥，则{c⋅c′|∀c∈C} 是ℜ 的非 零 理 想，则

下面讨论广义对称重量计数器所对应的MacWilliams 恒等式.

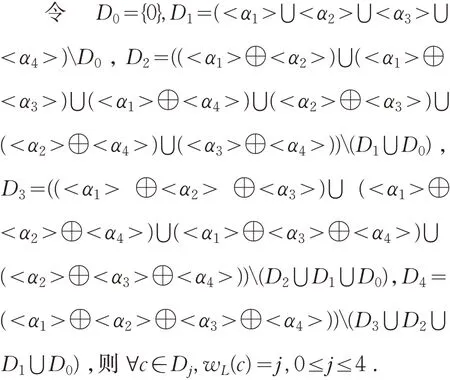
定理3 ∀c∈ℜ ，有

（1）如 果g∈D0，则j≤4；

（2）如果g∈D1，则

（3）如果g∈D2，则

（5）如果g∈D4，则

证 明（1）若g∈D0，则g=0 ，所 以

（2）若g∈D1，可 令则-1+3(ql-1)=3ql-4，同理可证其他各式.

（3）若g∈D2，可 令g∈(＜α1＞{0})⊕(＜α2＞{0})，则

同理可证式（4）和式（5）成立.

定理4 环ℜ 上的码C，则有SweC(X0,

证明 综合定理1 和定理2，得到SweC⊥(X0,j≤4，而由定理3 推出如下式子成立.

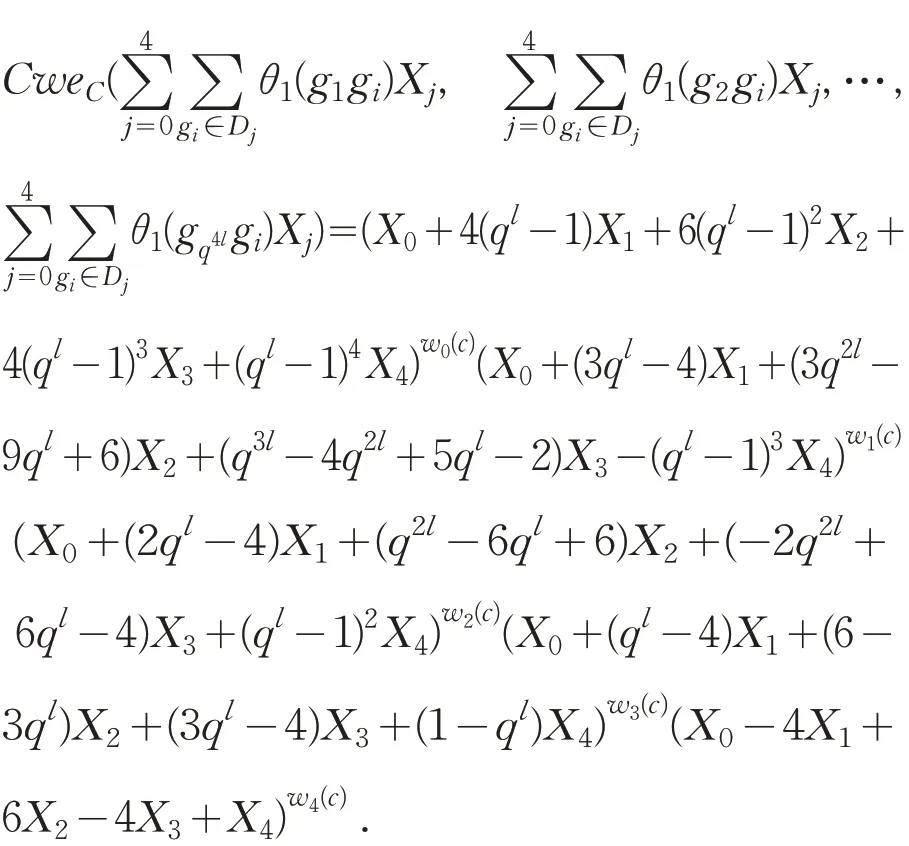
推论1 对环ℜ 上的码C，则HamC⊥(X,Y)=

推论2 对环ℜ 上的码C，则LeeC⊥(X,Y)=

例 如：环F3+uF3+vF3+uvF3上 的 码C={(0,0),(1,1),(2,2)}，长度为2.

（1）由推论2得LeeC⊥(X,Y)=X8+56X6Y2+336XY7+86Y8，所以C⊥的Lee 重量分布为

56X6Y2+ 112X5Y3+ 420X4Y4+ 560X3Y5+616X2Y6+336XY7+86Y8，则由上述两种方法均可求出C⊥的Lee 重量分布.