温度和激励磁场对磁巴克豪森跳跃平均体积的影响

(北京化工大学 数理学院，北京 100029)

铁磁材料在外部交变磁场的作用下，随着外磁场的增大，磁畴壁会多次发生跳跃式不可逆移动，材料内部产生非连续性的电磁脉冲，这种现象称为巴克豪森跳跃，也称为磁巴克豪森噪声(MBN)。磁巴克豪森噪声检测技术作为一种潜力巨大的电磁无损检测技术，在温度应力、残余应力检测等方面具有广阔的应用前景[1-4]。德国科学家HEINRICH BARKHAUSEN于1919年发现此现象。20世纪30年代，BOZORTH和DILLINGER等研究了巴克豪森跳跃，测量了几种金属和合金的巴克豪森跳跃平均体积(AVMBJ)，例如铁的AVMBJ的最大值为10-9cm3[5]。

在实践中发现AVMBJ不仅受激励磁场的影响，也与温度密切相关[6-7]。到目前为止，关于温度影响巴克豪森跳跃的研究还不多，AVMBJ与温度之间的明确数学关系仍缺乏研究。文章推导了AVMBJ，饱和磁化强度和温度之间的函数关系，用以解释AVMBJ和温度之间的理论关系，并在此基础上，推导出关于AVMBJ、温度和激励磁场强度间的明确数学表达式。

1 AVMBJ理论关系的研究

根据BOZORTH和DILLINGER之前的研究，磁巴克豪森跳跃平均体积AVMBJ的计算如式(1)所示[8]

(1)

式中:l为铁磁样品中产生巴克豪森跳跃的感应线圈的长度;μr为样品的可逆磁导率;A为线路常数;ρ为样品的电阻率;Bs为饱和磁通密度，Bs=4πMs，Ms为饱和磁化强度;dB/dt为磁感应强度的变化率;2为巴克豪森跳跃产生的均方电流，可以用试验装置测量。

根据铁磁学理论可知，磁畴不可逆位移产生的不可逆磁导率μirr为[6]

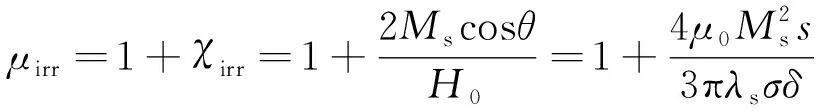
(2)

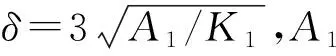
可逆磁导率μr为

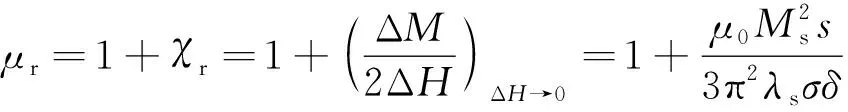
(3)

将式(2)和式(3)代入式(1)，可得

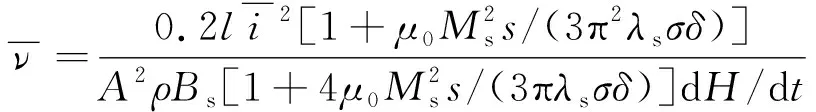
(4)

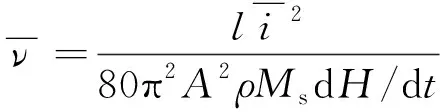
(5)

根据铁磁学理论可知，当温度T<0.8Tc(Tc为居里温度)时，某一温度的饱和磁化强度Ms和该温度下的自发磁化强度M(T)十分接近。所以根据“分子场”理论，饱和磁化强度Ms和温度T有以下的函数关系[9]

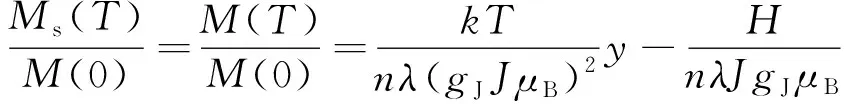
(6)

其中

M(0)=ngJμBJ

(7)

式中:M(0)为温度T趋近于0 K时的自发磁化强度;k为玻尔兹曼常数，其值为1.38×10-23J·K-1；μB为玻尔磁子，1.17×10-29Wb·m；n为原子数目；λ为“分子场”系数；J为总角动量量子数；H为磁场强度；gJ为朗德因子，其值一般在1至2之间；y为布里渊函数BJ(y)的自变量。

将式(6)中的Ms代入式(5)，可得AVMBJ与温度T和激励磁场强度H的关系为

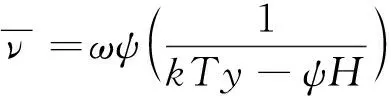
(8)

其中ω和ψ分别表示为

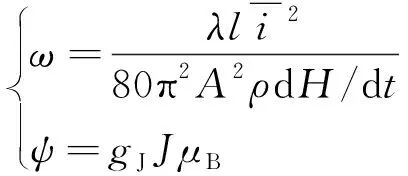
(9)

式(8)表示AVMBJ随着温度T的升高而减小，并随着磁场强度H的增大而增大。需要注意的是，上述分析的前提是T<0.8Tc。当温度T等于或超过0.8Tc时，饱和磁化强度Ms的数值和自发磁化强度M(T)的数值将不再接近[10]。式(8)解释了AVMBJ与温度T和磁场强度H的关系，并为应用磁巴克豪森技术进行无损检测中的温度补偿和磁场选择提供指导和参考。

2 理论模拟

在没有外应力的影响下，根据式(8)，在一固定激励磁场强度H下，AVMBJ与温度T之间的关系曲线如图1所示。

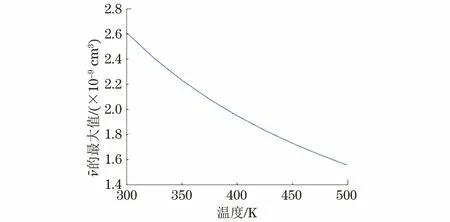
图1 AVMBJ()的最大值与温度的理论曲线

这里采用的激励磁场强度为1 200 A·m-1。图1表明AVMBJ的最大值随着温度T的升高而降低，且温度越高，AVMBJ下降趋势越缓和。

利用式(8)，图2所示为温度300 K时，AVMBJ最大值和激励磁场之间的关系曲线，可以看出AVMBJ的最大值在设定的激励磁场范围内，随着激励磁场的增大而增大。但相对于温度对最大值的影响而言，激励磁场对最大值的影响较小。图3为二者共同作用影响下，AVMBJ的最大值变化图像。

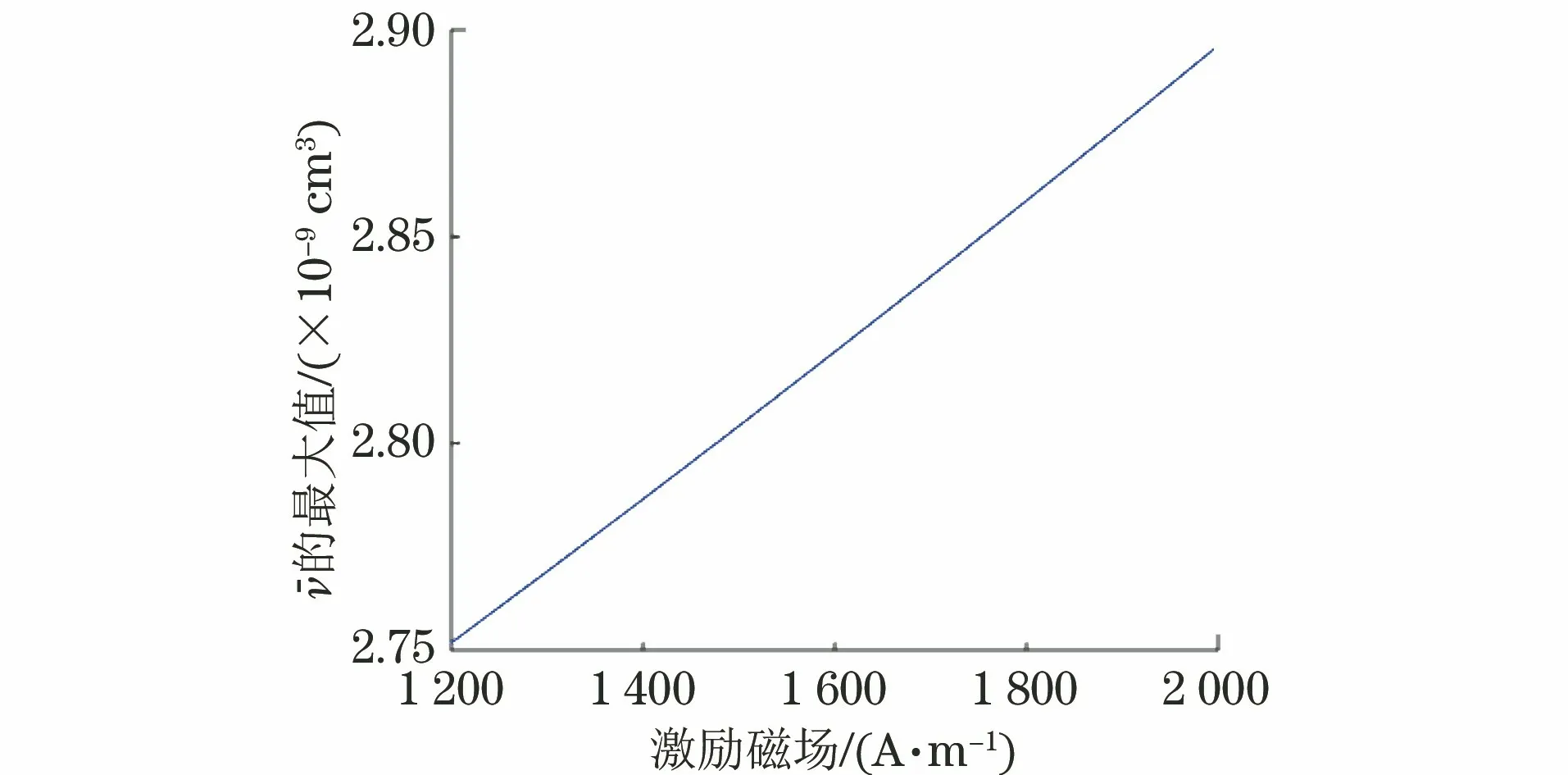
图2 AVMBJ ()的最大值与激励磁场的理论曲线

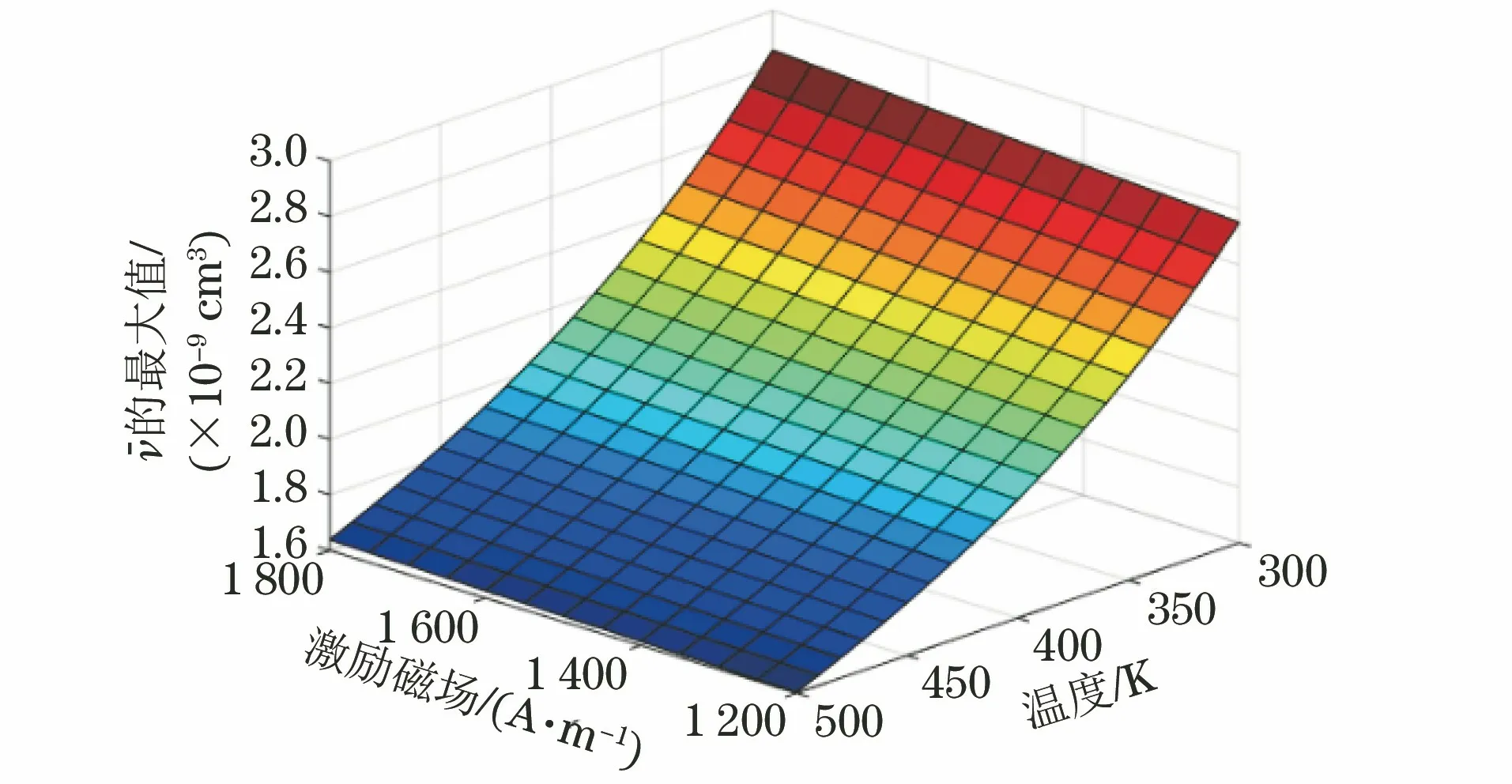
图3 在温度和激励磁场共同影响下,AVMBJ ()的最大值数值分布

3 试验测量

为了验证AVMBJ与温度和激励磁场的数值关系[式(8)]的正确性，在不同温度和不同激励磁场的情况下，分别对试块Q235进行试验。试验器材选用北京化工大学研制的巴克豪森噪声计IS-A200[11]。Q235钢是一种高性能碳素结构钢，广泛应用于零部件制造领域。

温度变化试验分别在300，325，350,375，400,425，450,475，500 K下进行，激励磁场变化试验分别在1 200,1 300,1 400,1 500,1 600,1 700,1 800,1 900 A·m-1下进行。

使用巴克豪森噪声计IS-A200测得MBN信号的均方根Vrms，根据均方根与AVMBJ的关系式[12][见式(10)],通过MATLAB软件计算可得AVMBJ的大小。

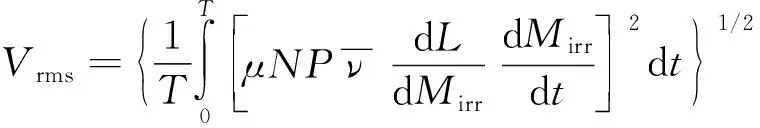
(10)

式中:N为线圈匝数;P为线圈截面积;μ为总磁导率;L为巴克豪森跳跃数量;Mirr为不可逆磁化强度。

图4为不同温度下AVMBJ最大值的测量值，拟合曲线及其理想曲线。由图4可以看出，测量出的AVMBJ最大值随着温度的增加而降低，且拟合曲线与理想曲线有良好的相关性。这是因为温度影响物质内部热运动的剧烈程度，热运动这种无规则的运动会破坏原子磁矩的整齐排列，从而影响物质的磁性[13]。

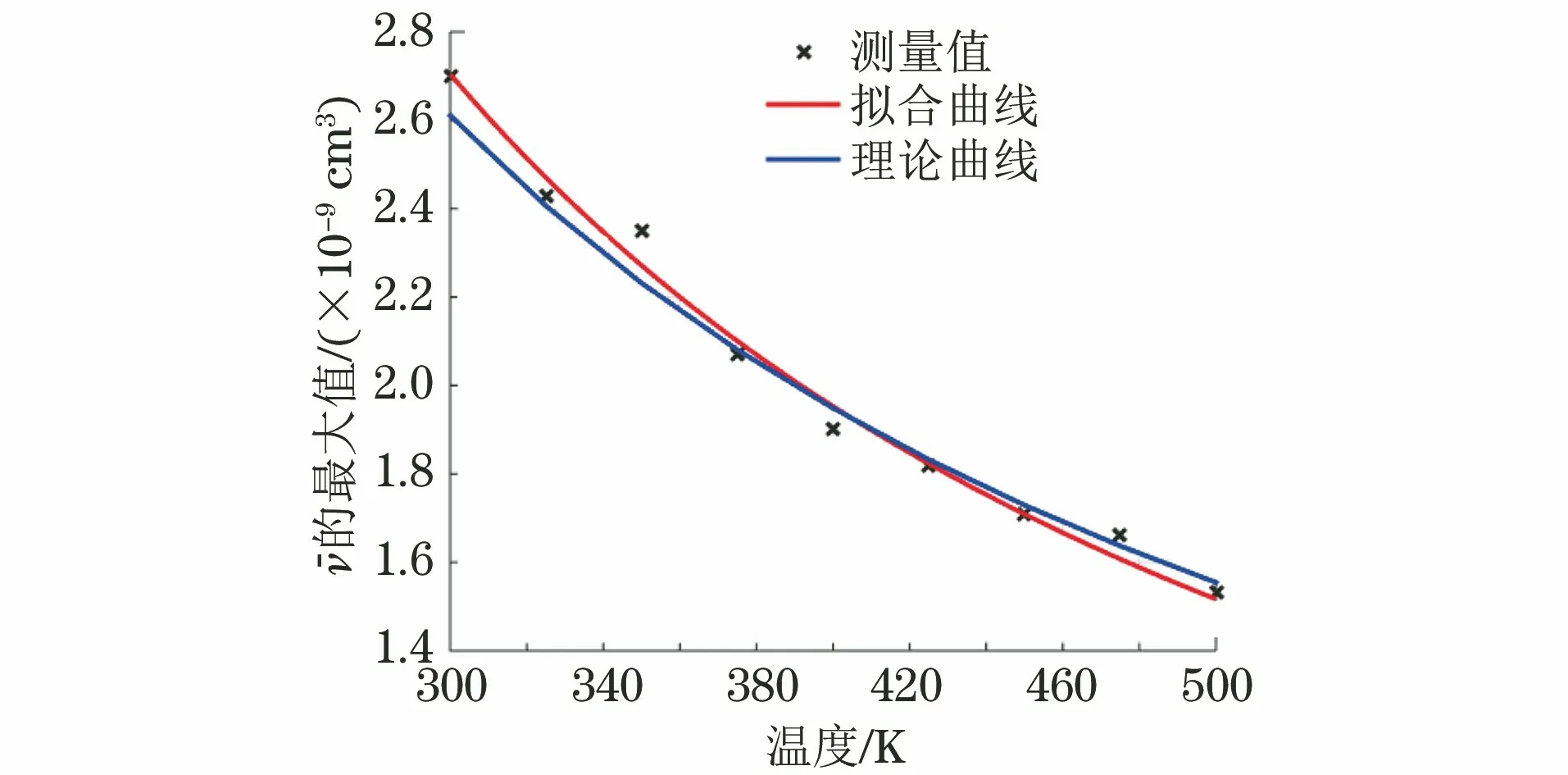
图4 不同温度下AVMBJ最大值的测量值，拟合曲线及理论曲线

图5为不同激励磁场下，AVMBJ最大值的测量值，拟合曲线及其理想曲线。由图5可以看出，测量出的AVMBJ最大值随着激励磁场的增大而增大,且拟合曲线与理想曲线的相关性良好。这是由于,与磁化方向成钝角的磁畴随着磁场的增大进行翻转，磁畴体积显著增加，从而造成AVMBJ的最大值增大。

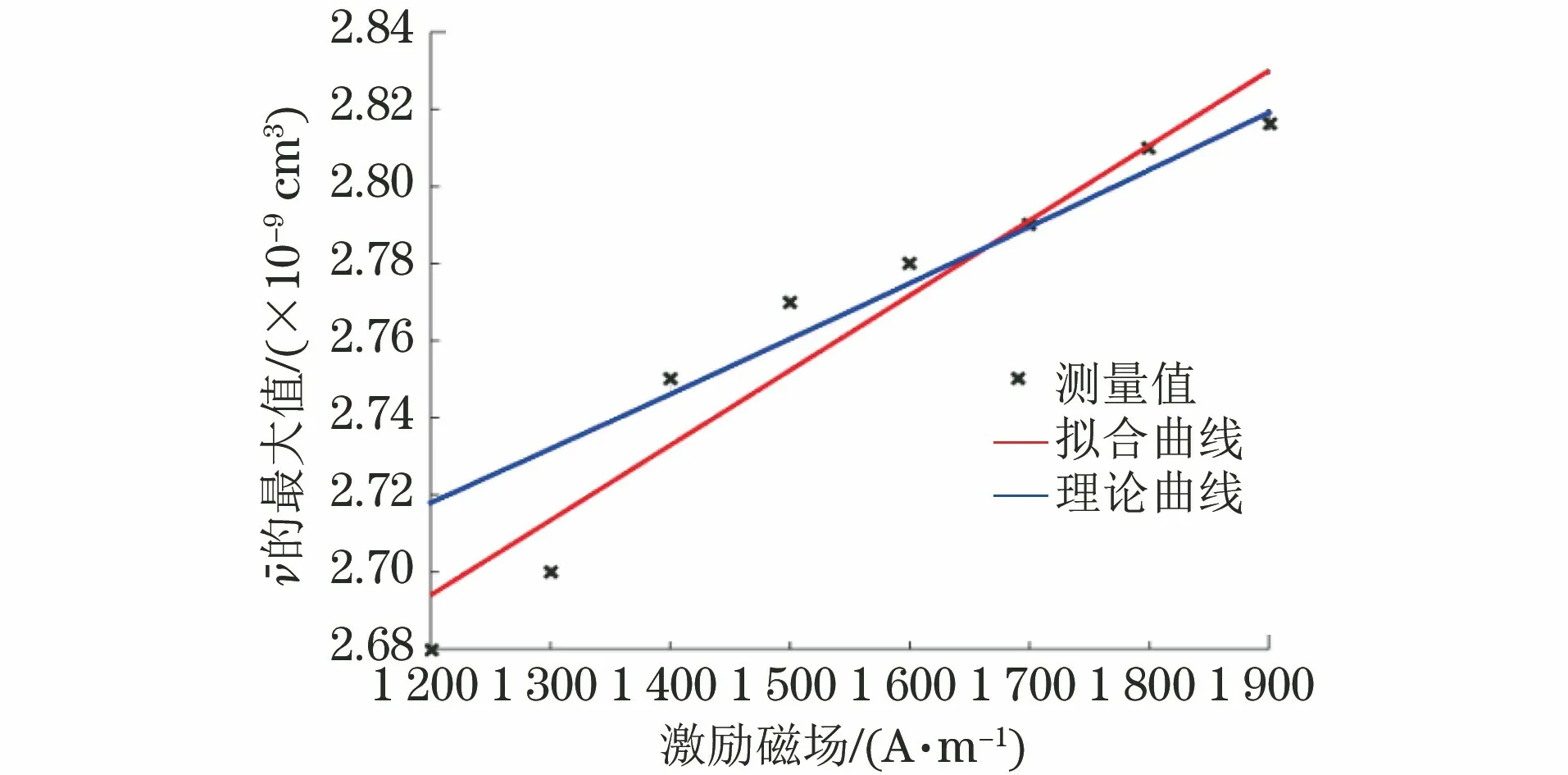
图5 不同激励磁场下AVMBJ最大值的测量值，拟合曲线及其理论曲线

式(2)中的H0为不可逆壁移的临界磁场强度，可用式(11)表示[14]。

(11)

随着磁场的增加，磁畴壁跳跃式壁移可能发生若干次，巴克豪森跳跃一直进行，最后可能遇到一个(dγ/dx)max的最大值，当磁场强度增加到大于该值时，磁畴壁就会无阻碍地大幅度移动，直到无可移动为止。

当壁移磁化是由随距离强弱变化的应力造成时，有

(12)

在多晶体中，θ取值范围为0π/2，因此cosθ的平均值为1/2，将式(12)代入式(11)得

(13)

式(12)就是不可逆壁移的最大临界磁场，是不可逆壁移磁化阶段和转动磁化阶段的分界点。过大的激励磁场H可能导致AVMBJ的快速饱和，较弱的激励磁场H可能难以引起畴壁的位移。因此磁巴克豪森信号检测应用于实践工程时，应采用临界磁场H0。

4 结论

(1) 文章推导出了关于AVMBJ、温度和激励磁场明确的数学表达式。当激励磁场为常数时，推断出AVMBJ最大值与温度之间的变化规律，可为利用磁巴克豪森检测方法进行工程测量时的温度补偿问题提供理论依据。

(2) 温度一定时，AVMBJ的最大值随着激励磁场的增大而增大。在工程实践中，当应用磁巴克豪森检测方法时，应采用临界磁场H0作为参考。临界磁场可以作为畴壁运动的基本能量，使畴壁运动。

(3) 在温度和激励磁场的作用下，温度对AVMBJ最大值的影响比激励磁场的影响更明显。因此，在磁巴克豪森检测方法的工程应用中，温度效应可根据文章推导的理论相关性进行合理地补偿。