基于模型参数不确定的欠驱动非对称自主水下航行器全局镇定控制研究

邸青， 周竞烨， 方凯， 姚佳琪， 李家旺

(宁波大学 海运学院, 浙江 宁波 315211)

0 引言

自主水下航行器(AUV)作为一种智能化的运载平台，凭借其隐蔽性强，搭载模块灵活，可无人执行危险任务等优点，在扫雷反潜、海洋科学调查、抢险救灾等领域获得了广泛的关注和应用[1-3]。其中，AUV的水平面镇定控制问题一直是相关领域研究的热点之一。欠驱动AUV属于非完整系统和强非线性系统[4]，由Brocket定理知此类系统无法通过光滑连续时不变控制算法实现镇定[5]，因此使得其控制器设计存在一定的困难。对此，国内外学者作了大量研究。李晔等[6]和关海滨等[7]通过微分同胚变换将AUV模型转换为级联形式的非线性系统，实现全局镇定控制器的设计。Fischer等[8]基于切换控制方法设计了时变光滑控制律以实现镇定控制。

但需要指出的是，以上研究均未考虑模型参数不确定性及未知海洋环境干扰对AUV运动控制的影响。为此，Xie等[9]针对水面运载器镇定控制存在的参数未知问题，通过李雅普诺夫函数递推设计方法估计模型参数，并利用反步法实现了对虚拟输入误差的镇定控制设计。Qiu等[10]通过构造自适应滑模控制律实现了模型参数不确定情况下的轨迹跟踪控制。Dong等[11]针对存在定向海流干扰因素的镇定问题，利用反步法设计了全局反馈控制律，但其假定海流方向恒定且与目标点艏向角一致，存在一定的局限性。此外，AUV一般都具有一定的非对称性，而上述研究均假设AUV前后和左右完全对称，忽略了惯性力矩阵和阻尼矩阵中非对角项元素的影响以及由此引发的动力学耦合特性，存在一定的建模误差和应用限制[12]。为此，Ma等[13]和陈功等[14]通过构造级联系统，使用反步法为非对称运载器设计了非连续反馈控制律，该方法收敛速度缓慢，无法严格镇定至平衡点。

在上述研究基础上，本文针对考虑参数不确定性和时变海流干扰作用下的非对称AUV水平面镇定控制问题进行研究。首先，考虑模型不确定性因素对控制的影响，提出一种自适应控制律估计未知模型参数。在此基础上，为消除非对称作用项引起艏摇和横荡方向上的耦合影响，通过全局坐标变换，将系统解耦为推进子系统和偏航子系统并分别进行控制设计。针对偏航子系统，通过引入一个2阶滤波器，使得偏航角速度在推进子系统状态未收敛至零点状态下始终具有持续激励特征。针对推进子系统，通过坐标变换，将其转换成较为简单形式进行控制设计。最后，通过数值仿真对所提出的控制策略进行验证。

1 AUV模型和问题描述

欠驱动AUV水平面运动包含艏摇、纵荡和横荡3个方向上的运动，仅通过前进推力和偏航力矩两个控制输入实现AUV的控制，其模型如图1所示。图1中：OExEyE表示大地坐标系；OBxByB表示随体坐标系，点OB通常取AUV重心或浮心的位置[15]。

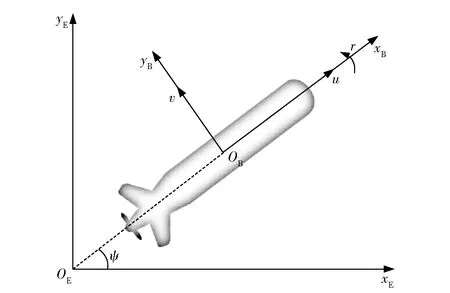
图1 欠驱动AUV水平面运动模型及坐标定义Fig.1 Horizontal plane motion model of underactuated AUV and definition of reference frames

因此，AUV的水平面运动方程[15]可表示为

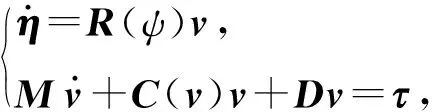
(1)

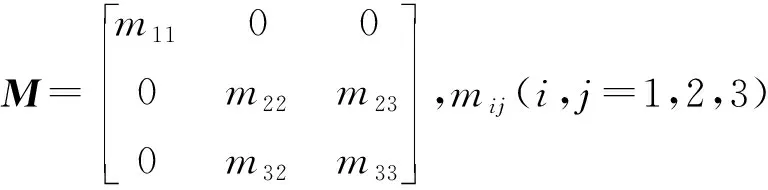
为便于后续分析，(1)式可表示为

(2)

(3)

式中：

(4)

2 欠驱动AUV镇定控制器设计

2.1 模型参数观测器设计

考虑到在现实中，虽然AUV的模型参数难以精确可知，但其数值所在区间往往是确定的。因此，本文给出以下假设：

假设1未知AUV模型参数ζui、ζvi、ζri满足ζhi∈[ζhimin,ζhimax]，其中ζhimin和ζhimax均为已知常数，h=u,v,r，i=1,2,…,5.

在此基础上，建立如下状态观测器：

(5)

(6)

式中：ku、kv、kr和kxE、kyE、kψ均为正常数；hi表示ζhi的观测值，其定义[16]为

(7)

Proj(αhi,hi)=

(8)

(9)

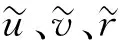
(10)

(11)

根据(10)式，对其求导可得

(12)

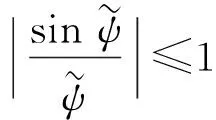
综上，定义李雅普诺夫函数V3=V1+V2并求导，可得

(13)

(14)

(15)

需要指出的是，根据观测误差的收敛性和(9)式，为了简化设计，(15)式中hi都可近似认为是常数。

2.2 模型转换

为了消除由非对称模型引起的艏摇方向和横荡方向的耦合影响，引入如下坐标变换：

(16)

(16)式代入(14)式和(15)式，此时，为了便于后续控制设计，可将(14)式和(15)式改写为

(17)

(18)

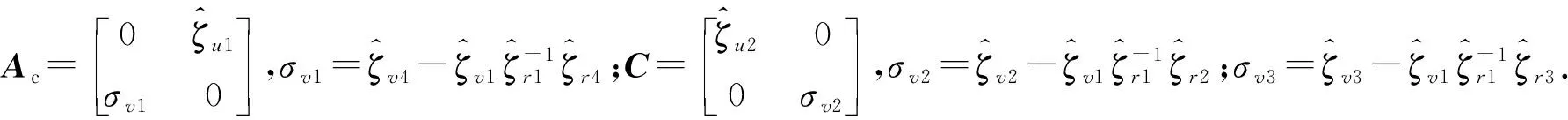
定义镇定误差[17]为

(19)

式中：(xEd,yEd)为期望镇定点坐标；ψd为期望艏向角。

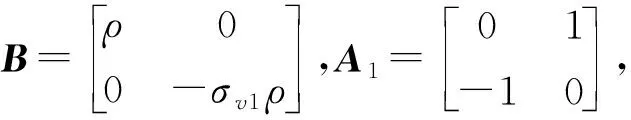
结合(17)式，对(19)式求导，可得

(20)

引入矩阵变换

(21)

并代入(17)式，可得

(22)

2.3 镇定控制器设计

基于上述分析，为方便控制器设计，本文将对两个子系统：偏航子系统Σ1:[,]T和推进子系统分别进行设计。

2.3.1 偏航子系统设计

首先，考虑到通常情况下AUV的偏航角ψ∈[0 rad,2π rad)，因此可对其作归一化处理[18]：

s=0.5π{1-sgn [cos]}sgn [sin]+

(23)

此时，偏航子系统Σ1运动模型(18)式可表示为

(24)

为了保证当推进子系统Σ2未实现镇定时角速度r符合持续激励条件，引入变量ϑψ，并令其满足以下2阶滤波器形式：

(25)

式中：Γ、χ、k3和k4为正常数。定义j=s+ϑψ，结合(24)式求导，可得

(26)

设计控制输入τr：

(27)

式中：k1、k2均为正常数。将(27)式代入(26)式，则有

(28)

2.3.2 推进子系统设计

针对推进子系统Σ2：

(29)

结合(20)式和(22)式可得

(30)

令ρ=-σv2/σv1，有

则(30)式可展开，并简化为

(31)

定义新的状态变量：

(32)

式中：β=tanh(kε2)，kε为正常数。

(32)式代入(31)式，可得

(33)

设计控制输入τu：

(34)

式中：kp为正常数。(34)式代入(33)式，可得

(35)

综上可知V5≥0，结合(35)式对V5求导，可得

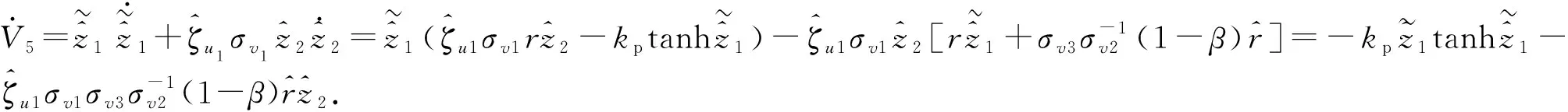
3 仿真结果及分析

为了对本文所提参数观测器和镇定控制算法的有效性进行验证，采用如下模型数据进行数值仿真实验[19]：m11=25.8 kg，m22=33.8 kg，m33=2.76 kg·m2，m23=6.2 kg·m，m32=6.2 kg，d11=0.925 7 kg/s，d22=2.890 9 kg/s，d23=0.2 kg·m/s，d32=0.2 kg/s，d33=0.5 kg·m2/s. 此外，不确定参数的界限值ζhimax、ζhimin分别定义为1.2ζhi和0.8ζhi. 设定AUV的初始状态为η=[20 m,-20 m,0 rad]T和ν=[0 m/s,0 m/s,0 rad/s]T，期望镇定状态为ηd=[0 m,0 m,0 rad]T和νd=[0 m/s,0 m/s,0 rad/s]T.

模型观测器参数设定为γu1=γv4=γr4=2 000,γu2=γu3=γu4=γv1=γv2=γv3=γr1=γr2=γr3=5，kxE=kyE=kψ=10,ku=kv=kr=1. 镇定控制器参数设定为k1=0.7，k2=2，k3=20，k4=1，kp=1，kε=10，χ=8和Γ=10. 仿真时间t设为400 s. 作为对比，本文以文献[9]中控制方法作为参照对象。无海流干扰情况下的AUV水平面镇定仿真结果如图2所示。

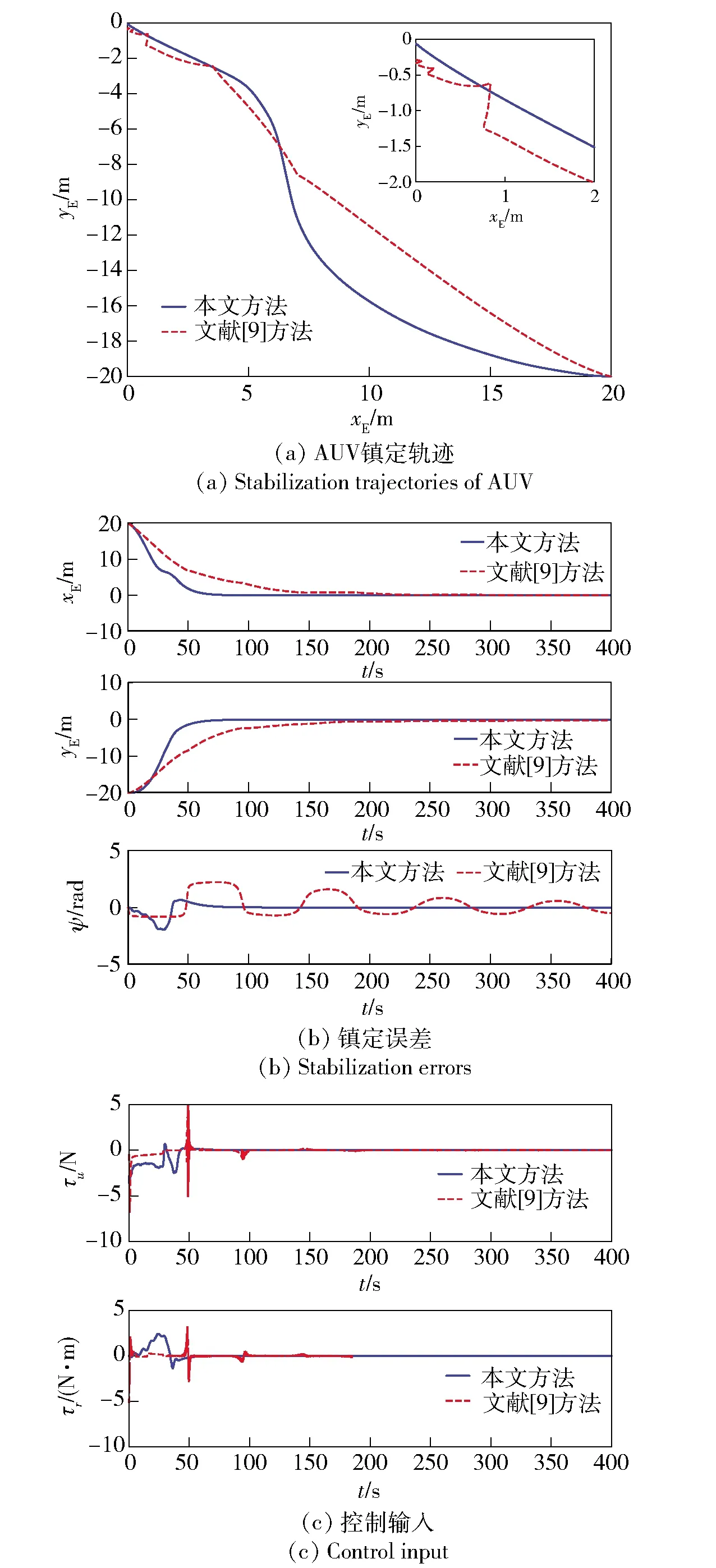
图2 无海流干扰情况下AUV水平面镇定控制仿真结果Fig.2 Simulated results of stabilization of AUVs on horizontal plane without current disturbance

由图2可知：在无海流干扰情况下文献[9]控制方法由于未考虑模型非对称因素影响，偏航角度出现的大幅度抖振，难以收敛至零点的情况；而本文控制方法由于考虑了模型非对称因素的影响，因此控制精度更高，镇定误差仅在100 s内即可基本收敛到零点附近一个较小的区间内；同时，本文方法的镇定轨迹更为光滑，且控制输入均较文献[9]方法微小，有效地减小了实际工况中可能出现的输入饱和情况的影响。

为了验证本文所设计模型参数观测器的性能，图3给出了AUV的速度观测误差变化情况。

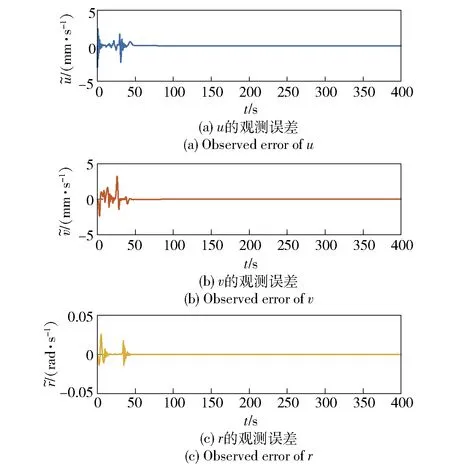
图3 模型参数观测器速度观测误差Fig.3 Velocity error of model parameter observer

由图3可知，各方向速度估计误差能够较快地收敛至零附近一个很小的领域，说明本文设计的模型参数观测器所获取的模型参数估计值可较好地逼近其实际值，其有效性得到了验证。

为了进一步验证本文控制器对未知时变环境干扰的鲁棒性，本文针对存在时变海流干扰情况进行了数值仿真。海流干扰下AUV的位置方程可改写为

(36)

式中：vxE和vyE分别表示大地坐标系OExEyE中xE轴方向和yE轴方向上的海流速度，其具体数值设定为

(37)

仿真结果如图4所示。由图4可知，与文献[9]方法相比，当存在时变海流干扰时，本文设计的控制方法依然可以在保持较快的镇定误差收敛速度，较好的控制精度和光滑的镇定轨迹前提下，以较小的控制输入实现镇定控制目标，说明本文控制方法具有较好的抵抗外界干扰鲁棒性能。

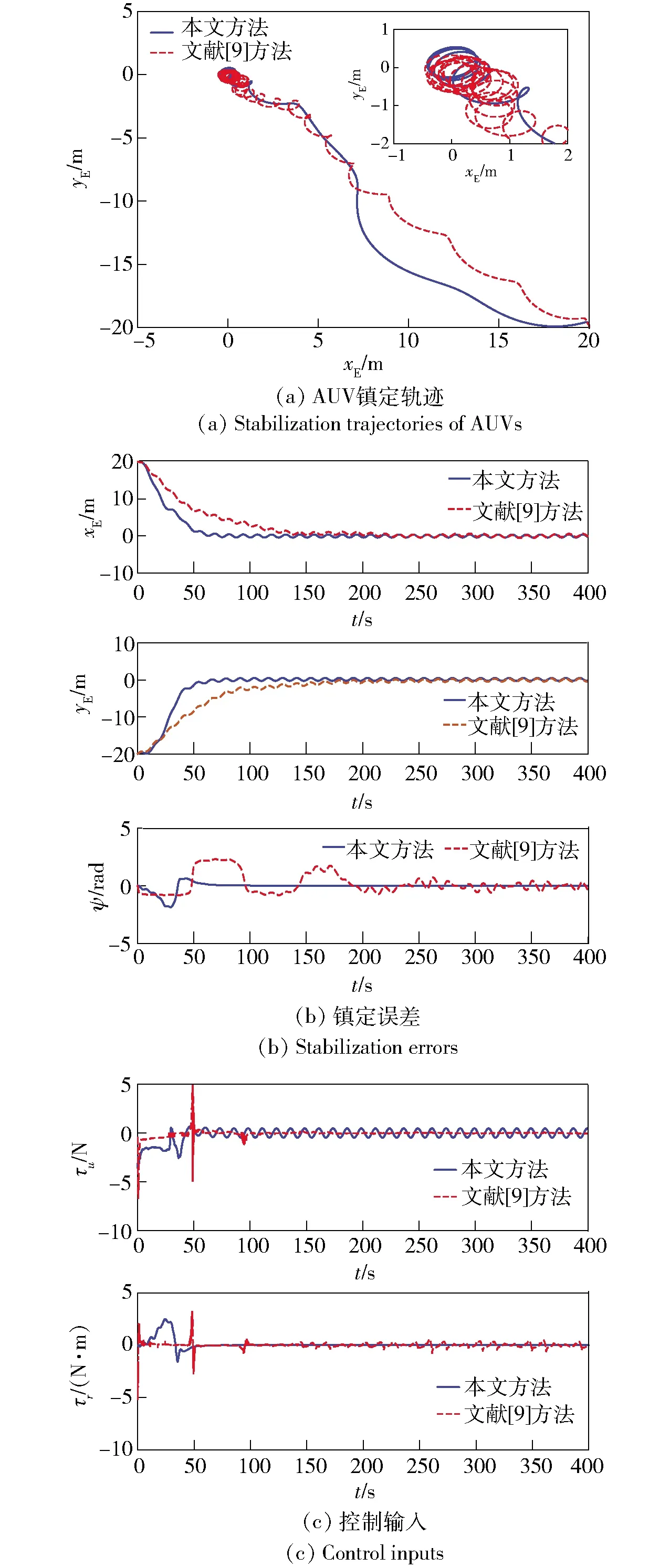
图4 时变海流干扰作用下AUV水平面镇定控制仿真结果Fig.4 Simulated results of stabilization of AUV on horizontal plane with time-varying current disturbance

4 结论

本文研究了模型参数不确定情况下欠驱动非对称AUV的水平面镇定控制问题。通过设计参数自适应律对未知参数进行估计，在考虑非对称模型影响情况下，利用坐标变换将系统分为两个级联子系统分别进行控制设计。最后基于李雅普诺夫理论证明了系统的全局稳定性，通过与文献[9]控制方法的仿真实验对比，验证了本文所提控制策略的有效性和可靠性。得出以下主要结论：

1)本文所设计的控制算法考虑了模型非对称因素的影响，可实现欠驱动AUV水平面运动镇定误差的全局渐近稳定，且与现有类似算法相比具有较好的控制性能。

2)基于参数自适应律的模型误差观测算法能够有效地减小模型不确定对系统控制性能的影响。此外，本文控制器在考虑外界环境干扰情况下仍具有较好的控制精度和光滑的镇定轨迹，说明该方法对环境干扰具有良好的鲁棒性能。

后续工作包括探索将本文控制方法拓展至三维空间镇定问题和进一步考虑诸如输入饱和等限制条件下的控制问题。